前言

更好的阅读体验：https://blog.dwj601.cn/GPA/4th-term/ProbAndStat/

笔记范围：五至八章。一至四章请跳转：https://blog.csdn.net/qq_73408594/article/details/140190525

教材情况：

课程名称	选用教材	版次	作者	出版社	ISBN号
概率论与数理统计Ⅰ	概率论与数理统计	第一版	刘国祥王晓谦 等主编	科学出版社	978-7-03-038317-4

学习资源：

• 📺 视频资源：《概率论与数理统计》教学视频全集（宋浩）
• 📖 教材答案：https://pan.baidu.com/s/1yeC0rxatHaLeNHQaW85Kpw?pwd=448w

第5章 大数定律与中心极限定理

{% note light %}

本章只需要知道一个独立同分布中心极限定理即可，至于棣莫弗-拉普拉斯中心极限定理其实就是前者的 { X i } i = 1 ∞ \{X_i\}_{i=1}^{\infty} {Xi​}i=1∞​ 服从伯努利 $n$ 重分布罢了。

{% endnote %}

独立同分布中心极限定理

定义： { X i } i = 1 ∞ \{X_i\}_{i=1}^{\infty} {Xi​}i=1∞​ 独立同分布且非零方差，其中 $E{X}_i=\mu ,D{X}_i={\sigma }^2$，则有：
$$\begin{array}{rl}\sum _{i=1}^n{X}_i& \sim N(\sum _{i=1}^n(E{X}_i),\sum _{i=1}^n(D{X}_i))\\ & \sim N(n\mu ,n{\sigma }^2)\end{array}$$
解释：其实就是对于独立同分布的随机事件 $X_i$，在事件数 $n$ 足够大时，就近似为正态分布（术语叫做依分布）。这样就可以很方便利用正态分布的性质计算当前事件的概率。至于棣莫弗-拉普拉斯中心极限定理就是上述 $\mu =p,{\sigma }^2=p(1-p)$ 的特殊情况罢了

第6章 数理统计的基本概念

{% note light %}

开始统计学之旅。

{% endnote %}

6.1 总体与样本

类比 ML：数据集=总体，样本=样本。

我们只研究一种样本：简单随机样本 $(X_1,X_2,...,X_n)$。符合下列两种特点：

1. $(X_1,X_2,...,X_n)$ 相互独立
2. $(X_1,X_2,...,X_n)$ 同分布

同样的，我们研究总体 $X$ 的分布与概率密度，一般概率密度会直接给，需要我们在此基础之上研究所有样本的联合密度：

• 分布：由于样本相互独立，故：
  $$F(x_1,x_2,...,x_n)=F(x_1)F(x_2)\cdots F(x_n)$$

• 联合密度：同样由于样本相互独立，故：
  $$p(x_1,x_2,...,x_n)=p(x_1)p(x_2)\cdots p(x_n)$$

6.2 经验分布与频率直方图

经验分布函数是利用样本得到的。也是给区间然后统计样本频度进而计算频率，只不过区间长度不是固定的。

频率直方图就是选定固定的区间长度，然后统计频度进而计算频率作图。

6.3 统计量

统计量定义：关于样本不含未知数的表达式。

常见统计量：假设 $(X_1,X_2,...,X_n)$ 为来自总体 $X$ 的简单随机样本

一、样本均值和样本方差

• 样本均值：$\overline{X}=\frac{1}{n}\sum _{i=1}^n{X}_i$

• 样本方差：$S_0^2=\frac{1}{n}\sum _{i=1}^n(X_i-\overline{X}{)}^2=\frac{1}{n}\sum _{i=1}^n{X}_i^2-{\overline{X}}^2$

• 样本标准差：$S_0=\sqrt{S_0^2}$

• 修正样本方差：$S^2=\frac{1}{n-1}\sum _{i=1}^n(X_i-\overline{X}{)}^2$

• 修正样本标准差：$S=\sqrt{S^2}$
  {% fold light @推导 %}

  设总体 $X$ 的数学期望和方差分别为 $\mu$ 和 ${\sigma }^2$，$(X_1,X_2,...,X_n)$ 是简单随机样本，则：

  

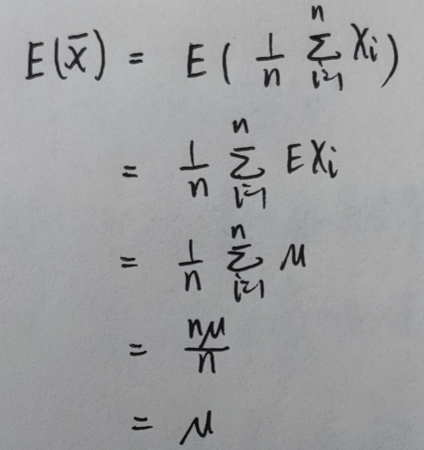
  即：样本均值的数学期望 $=$ 总体的数学期望

  

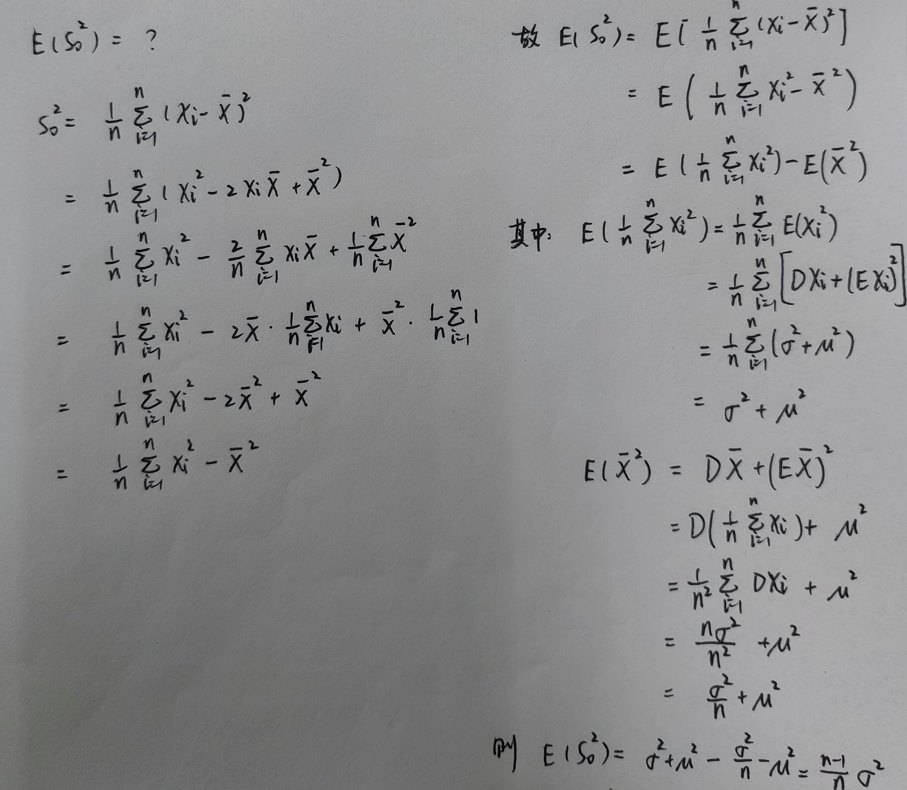
  即：样本方差的数学期望 $\ne$ 总体的数学期望

  

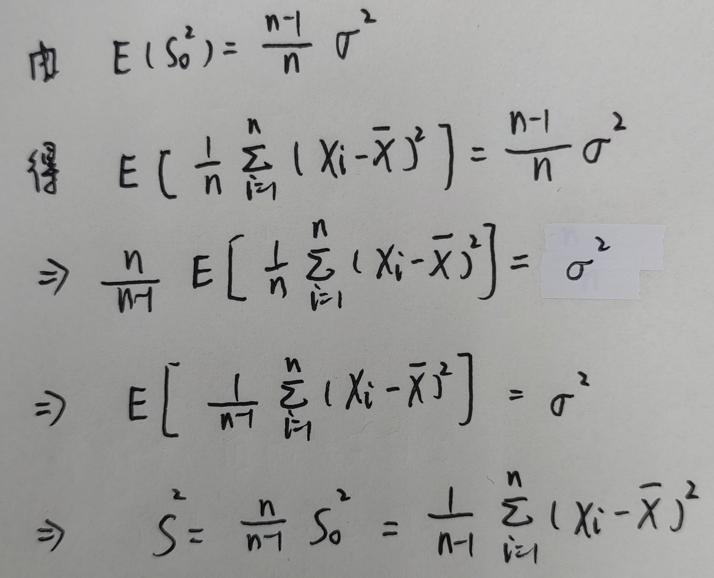
  上图即：修正样本方差推导

  {% endfold %}

• 样本 $k$ 阶原点矩：$A_k=\frac{1}{n}\sum _{i=1}^n{X}_i^k,k=1,2,\cdots$

• 样本 $k$ 阶中心矩：$B_k=\frac{1}{n}\sum _{i=1}^n(X_i-\overline{X}{)}^k,k=2,3,\cdots$

二、次序统计量

• 序列最小值
• 序列最大值
• 极差 = 序列最大值 - 序列最小值

6.4 正态总体抽样分布定理

{% note light %}

时刻牢记一句话：构造性定义！

{% endnote %}

6.4.1 卡方分布、t 分布、F 分布

分位数

• 我们定义实数 ${\lambda }_{\alpha }$ 为随机变量 $X$ 的上侧 $\alpha$ 分位数（点）当且仅当 $P(X>{\lambda }_{\alpha })=\alpha$​
• 我们定义实数 ${\lambda }_{1-\beta }$ 为随机变量 $X$ 的下侧 $\beta$ 分位数（点）当且仅当 $P(X<{\lambda }_{1-\beta })=\beta$

${\chi }^2$ 分布

{% fold light @密度函数图像 %}

{% endfold %}

定义：

• 对于 $n$ 个独立同分布的标准正态随机变量 $X_1,X_2,\cdots ,X_n$，若 $Y=X_1^2+X_2^2+\cdots +X_n^2$
• 则 $Y$ 服从自由度为 $n$ 的 ${\chi }^2$ 分布，记作：$Y\sim {\chi }^2(n)$

性质：

• 可加性：若 $Y_1\sim {\chi }^2(n_1),Y_2\sim {\chi }^2(n_2)$ 且 $Y_1,Y_2$ 相互独立，则 $Y_1+Y_2\sim {\chi }^2(n_1+n_2)$

• 统计性：对于 $Y\sim {\chi }^2(n)$，有 $EY=n,DY=2n$

  {% fold light @推导 %}
  EY 的推导利用：$E{X}^2=DX-(EX{)}^2$

  

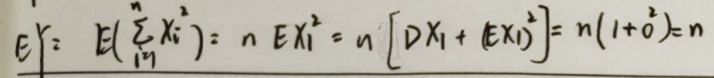
  DY 的推导利用：方差计算公式、随机变量函数的数学期望进行计算

  

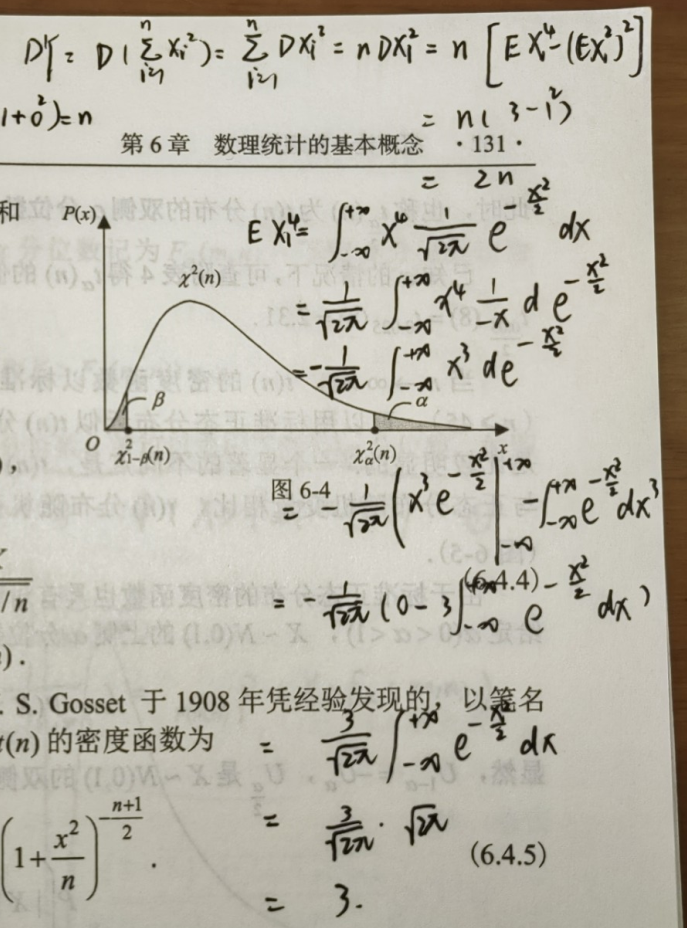
  {% endfold %}

$t$ 分布

{% fold light @密度函数图像 %}

{% endfold %}

定义：

• 若随机变量 $X\sim N(0,1),Y\sim {\chi }^2(n)$ 且 $X,Y$ 相互独立
• 则称随机变量 $T=\frac{X}{\sqrt{Y/n}}$ 为服从自由度为 $n$ 的 $t$ 分布，记作 $T\sim t(n)$​

性质：

• 密度函数是偶函数，具备对称性

$F$ 分布

{% fold light @密度函数图像 %}

{% endfold %}

定义：

• 若随机变量 $X\sim {\chi }^2(m),Y\sim {\chi }^2(n)$ 且相互独立
• 则称随机变量 $G=\frac{X/m}{Y/n}$ 服从自由度为 $(m,n)$ 的 $F$ 分布，记作 $G\sim F(m,n)$​

性质：

• 倒数自由度转换：$\frac{1}{G}\sim F(n,m)$
• 三变性质：$F_{1-\alpha }(m,n)={\left[F_{\alpha }(n,m)\right]}^{-1}$

6.4.2 正态总体抽样分布基本定理

设 $X_1,X_2,\cdots ,X_n$ 是来自正态总体 $N(\mu ,{\sigma }^2)$ 的简单随机样本，$\overline{X},S^2$ 分别是样本均值和修正样本方差。则有：

定理：

• $\overline{X}\sim N(\mu ,\frac{{\sigma }^2}{n})$
• $\frac{(n-1)S^2}{{\sigma }^2}\sim {\chi }^2(n-1)$
• $\overline{X}$ 和 $S^2$ 相互独立

推论：

• $\frac{\sqrt{n}(\overline{X}-\mu )}{S}\sim t(n-1)$

第7章 参数估计

{% note light %}

有些时候我们知道数据的分布类型，但是不清楚表达式中的某些参数，这就需要我们利用「已有的样本」对分布表达式中的参数进行估计。本章我们将从点估计、估计评价、区间估计三部分出发进行介绍。

{% endnote %}

7.1 点估计

{% note light %}

所谓点估计策略，就是直接给出参数的一个估计值。本目我们介绍点估计策略中的两个方法：矩估计法、极大似然估计法。

{% endnote %}

7.1.1 矩估计法

其实就一句话：我们用样本的原点矩 $A_k$ 来代替总体 $E(X^k)$，$k$ 个未知参数就需要用到 $k$ 个原点矩：
$$E(X^k)=A_k=\frac{1}{n}\sum _{i=1}^n{X}_i^k$$

7.1.2 极大似然估计法

基本原理是：在当前样本数据的局面下，我们希望找到合适的参数使得当前的样本分布情况发生的概率最大。由于各样本相互独立，因此我们可以用连乘的概率公式来计算当前局面的概率值：
$$L(\theta ;x_1,x_2,\cdots ,x_n)$$
上述 $L(\theta ;x_1,x_2,\cdots ,x_n)$ 即似然函数，目标就是选择适当的参数 $\theta$ 来最大化似然函数。无论是离散性还是连续型，都可以采用下面的方式来计算极大似然估计：

1. 写出似然函数 $L(\theta )$
2. 将上述似然函数取对数
3. 求对数似然函数关于所有未知参数的偏导并计算极值点
4. 解出参数关于样本统计量的表达式

离散型随机变量的似然函数表达式
$$L(\theta )=\prod _{i=1}^{n}p(x_i;\theta )=\prod _{i=1}^{n}P(X_i=x_i)$$
连续型随机变量的似然函数表达式
$$L(\theta )=\prod _{i=1}^{n}p(x_i;\theta )$$
可以看出极大似然估计本质上就是一个多元函数求极值的问题。特别地，当我们没法得到参数关于样本统计量的表达式 $L(\theta )$ 时，可以直接从定义域、原函数恒增或恒减等角度出发求解这个多元函数的极值。

7.2 估计量的评价标准

{% note light %}

如何衡量不同的点估计方法好坏？我们引入三种点估计量的评价指标：无偏性、有效性、一致性。其中一致性一笔带过，不做详细讨论。补充一点，参数的估计量 $\theta$ 是关于样本的统计量，因此可以对其进行求期望、方差等操作。

{% endnote %}

7.2.1 无偏性

顾名思义，就是希望估计出来的参数量尽可能不偏离真实值。我们定义满足下式的估计量 $\hat{\theta }$ 为真实参数的无偏估计：
$$E\hat{\theta }=\theta$$

7.2.2 有效性

有效性是基于比较的定义方法。对于两个无偏估计 ${\hat{\theta }}_1,{\hat{\theta }}_2$，谁的方差越小谁就越有效。即若 $D({\hat{\theta }}_1),D({\hat{\theta }}_2)$ 满足下式，则称 ${\hat{\theta }}_1$ 更有效
$$D({\hat{\theta }}_1)<D({\hat{\theta }}_2)$$

7.2.3 一致性

即当样本容量 n 趋近于无穷时，参数的估计值也能趋近于真实值，则称该估计量 $\hat{\theta }$ 为 $\theta$ 的一致估计量

7.3 区间估计

{% note light %}

由于点估计只能进行比较，无法对单一估计进行性能度量。因此引入「主元法」的概念与「区间估计」策略

{% endnote %}

7.3.1 基本概念

可靠程度：参数估计区间越长，可靠程度越高

精确程度：参数估计区间越短，可靠程度越高

7.3.2 区间估计常用方法之主元法

主元法的核心逻辑就一个：在已知数据总体分布的情况下，构造一个关于样本 $X$ 和待估参数 $\theta$ 的函数 $Z(X,\theta )$，然后利用置信度和总体分布函数，通过查表得到 $Z(X,\theta )$ 的取值范围，最后通过移项变形得到待估参数的区间，也就是估计区间。

7.3.3 正态总体的区间估计

我们只需要掌握「一个总体服从正态分布」的情况。这种情况下的区间估计分为三种，其中估计均值 $\mu$ 有 2 种，估计方差 ${\sigma }^2$ 有 1 种。估计的逻辑我总结为了以下三步：

1. 构造主元 $Z(X,\theta )$
2. 利用置信度 $1-\alpha$ 计算主元 $Z$ 的取值范围
3. 对主元 $Z$ 的取值范围移项得到参数 $\theta$ 的取值范围

为了提升区间估计的可信度，我们希望上述第 2 步计算出来的关于主元的取值范围尽可能准确。我们不加证明的给出以下结论：取主元的取值范围为 主元服从的分布的上下 $\frac{\alpha }{2}$ 分位数之间。

(一) 求 $\mu$ 的置信区间，${\sigma }^2$ 已知

构造主元 $Z(X,\theta )$：
$$Z=\frac{\overline{X}-\mu }{\sigma /\sqrt{n}}\sim N(0,1)$$
利用置信度 $1-\alpha$ 计算主元 $Z$ 的取值范围：
$$\begin{array}{rl}P(|Z|\le \lambda )& =1-\alpha \\ & \downarrow \\ Z\in [-\lambda ,\lambda ]& =[-u_{\frac{\alpha }{2}},u_{\frac{\alpha }{2}}]\end{array}$$
对主元 $Z$ 的取值范围移项得到参数 $\theta$ 的取值范围：
$$\overline{X}-\frac{\sigma }{\sqrt{n}}{u}_{\frac{\alpha }{2}}\le \mu \le \overline{X}+\frac{\sigma }{\sqrt{n}}{u}_{\frac{\alpha }{2}}$$
(二) 求 $\mu$ 的置信区间，${\sigma }^2$ 未知

构造主元 $Z(X,\theta )$：
$$Z=\frac{\overline{X}-\mu }{S/\sqrt{n}}\sim t(n-1)$$
利用置信度 $1-\alpha$ 计算主元 $Z$ 的取值范围：
$$\begin{array}{rl}P(|Z|\le \lambda )& =1-\alpha \\ & \downarrow \\ Z\in [-\lambda ,\lambda ]& =[-t_{\frac{\alpha }{2}}(n-1),t_{\frac{\alpha }{2}}(n-1)]\end{array}$$
对主元 $Z$ 的取值范围移项得到参数 $\theta$ 的取值范围：
$$\overline{X}-\frac{S}{\sqrt{n}}{t}_{\frac{\alpha }{2}}(n-1)\le \mu \le \overline{X}+\frac{S}{\sqrt{n}}{t}_{\frac{\alpha }{2}}(n-1)$$
(三) 求 ${\sigma }^2$ 的置信区间，构造的主元与总体均值无关，因此不需要考虑 $\mu$ 的情况：

构造主元 $Z(X,\theta )$：
$$Z=\frac{(n-1)S^2}{{\sigma }^2}\sim {\chi }^2(n-1)$$
利用置信度 $1-\alpha$ 计算主元 $Z$ 的取值范围：
$$\begin{array}{rl}P({\lambda }_1\le Z\le {\lambda }_2)& =1-\alpha \\ & \downarrow \\ Z\in [{\lambda }_1,{\lambda }_2]& =[{\chi }_{1-\frac{\alpha }{2}}^2(n-1),{\chi }_{\frac{\alpha }{2}}^2(n-1)]\end{array}$$
对主元 $Z$ 的取值范围移项得到参数 $\theta$ 的取值范围：
$$\frac{(n-1)S^2}{{\chi }_{\frac{\alpha }{2}}^2(n-1)}\le {\sigma }^2\le \frac{(n-1)S^2}{{\chi }_{1-\frac{\alpha }{2}}^2(n-1)}$$

第8章 假设检验

{% note light %}

第 7 章的参数估计是在总体分布已知且未知分布表达式中某些参数的情况下，基于「抽取的少量样本」进行的参数估计。

现在的局面同样，我们已知总体分布和不完整的分布表达式参数。现在需要我们利用抽取的少量样本判断样本所在向量空间是否符合某种性质。本章的「假设检验」策略就是为了解决上述情况而诞生的。我们主要讨论单个正态总体的情况并针对均值和方差两个参数进行假设和检验：

• 假设均值满足某种趋势，利用已知数据判断假设是否成立
• 假设方差满足某种趋势，利用已知数据判断假设是否成立

{% endnote %}

8.1 假设检验的基本概念

基本思想：首先做出假设并构造一个关于样本观察值和已知参数的检验统计量，接着计算假设发生的情况下小概率事件发生时该检验统计量的取值范围（拒绝域），最终代入已知样本数据判断计算结果是否在拒绝域内。如果在，则说明在当前假设的情况下小概率事件发生了，对应的假设为假；反之说明假设为真。

为了量化「小概率事件发生」这个指标，我们引入显著性水平 $\alpha$ 这一概念。该参数为一个很小的正数，定义为「小概率事件发生」的概率上界。

基于数据的实验导致我们无法避免错误，因此我们定义以下两类错误：

• 第一类错误：弃真错误。即假设正确，但由于数据采样不合理导致拒绝了真实的假设
• 第二类错误：存伪错误。即假设错误，同样因为数据的不合理导致接受了错误的假设

8.2 单个正态总体均值的假设检验

设 $X_1,X_2,\cdots ,X_n$ 是来自正态总体 $N(\mu ,{\sigma }^2)$ 的简单随机样本。后续进行假设判定计算统计量 $Z$ 的真实值时，若总体均值 $\mu$ 已知就直接代入，若未知题目也一定会给一个阈值，代这个阈值即可。

当总体方差 ${\sigma }^2$ 已知时，我们构造样本统计量 $Z$ 为正态分布：
$$Z=\frac{\overline{X}-\mu }{\sigma /\sqrt{n}}\sim N(0,1)$$

• 检验是否则求解双侧 $\alpha$ 分位数
• 检验单边则求解单侧 $\alpha$ 分位数

当总体方差 ${\sigma }^2$ 未知时，我们构造样本统计量 $Z$ 为 $t$ 分布：
$$Z=\frac{\overline{X}-\mu }{S/\sqrt{n}}\sim t(n-1)$$
{% note warning %}

注：之所以这样构造是因为当总体 $\sigma$ 未知时，上一个方法构造的主元已经不再是统计量，我们需要找到能够代替未知参数 $\sigma$ 的变量，这里就采用其无偏估计「修正样本方差 $S^2$」来代替 ${\sigma }^2$。也是说直接拿样本的修正方差来代替总体的方差了。

{% endnote %}

• 检验是否则求解双侧 $\alpha$ 分位数
• 检验单边则求解单侧 $\alpha$ 分位数

8.3 单个正态总体方差的假设检验

设 $X_1,X_2,\cdots ,X_n$ 是来自正态总体 $N(\mu ,{\sigma }^2)$ 的简单随机样本。后续进行假设判定计算统计量 $Z$ 的真实值时，若总体方差 ${\sigma }^2$ 已知就直接代入，若未知题目也一定会给一个阈值，代这个阈值即可。

我们直接构造样本统计量 $Z$ 为 ${\chi }^2$ 分布：
$$Z=\frac{(n-1)S^2}{{\sigma }^2}\sim {\chi }^2(n-1)$$

• 检验是否则求解双侧 $\alpha$ 分位数
• 检验单边则求解单侧 $\alpha$ 分位数