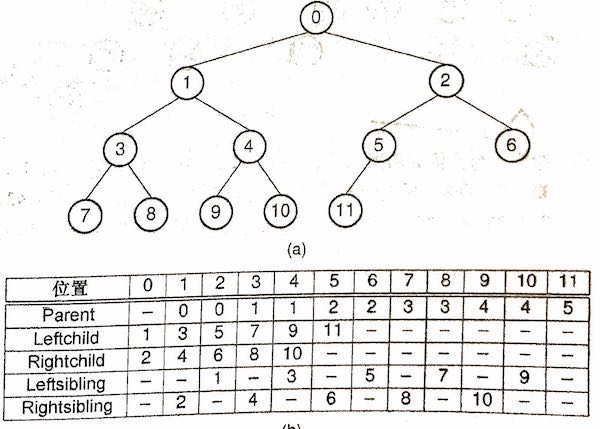
今天写了几道题目
最近,一年级学生马克西姆学习了科拉兹猜想,但他在讲课时没有太注意,所以他认为猜想中提到了以下过程:
有一个变量 $$$x$$$ 和一个常数 $$$y$$$ 。下面的操作要执行 $$$k$$$ 次:
- 将 $$$x$$$ 增加 $$$1$$$ ,然后
- 当数字 $$$x$$$ 能被 $$$y$$$ 整除时,再除以 $$$y$$$ 。
请注意,这两个操作都是在一次操作中依次进行的。
例如,如果数字 $$$x = 16$$$ 、 $$$y = 3$$$ 和 $$$k = 2$$$ ,那么经过一次运算后, $$$x$$$ 变成了 $$$17$$$ ,而经过另一次运算后, $$$x$$$ 变成了 $$$2$$$ ,因为加一后, $$$x = 18$$$ 可以被 $$$3$$$ 整除两次。
鉴于初始值为 $$$x$$$ 、 $$$y$$$ 和 $$$k$$$ ,马克西姆想知道 $$$x$$$ 的最终值是多少。
思路是先凑到y的倍数,在除y,考虑到时间的问题,所以基于二分的思想设置了一个s每次对自己平方再判断能不能整除,复杂度从n降到了logn,一直除到a<b,再凑到a等于b,再除就是1,那么就是对剩下的c的部分对(b-1)取余再加一即为答案。
#include<bits/stdc++.h>
#include<algorithm>
#define ll long long
#define max_int 2147483647
#define max_ll 9223372036854775807
using namespace std;
int main()
{
ios::sync_with_stdio(false);
cin.tie(0);
int all;
cin>>all;
while(all--){
ll a,b,c;
cin>>a>>b>>c;
int bo=1;
while(c){
ll yu=b-a%b;
ll s=b,s2=b*b;
if(yu<=c){
c-=yu;
a+=yu;
}
else{
cout<<a+c<<endl;
bo=0;
break;
}
while(a%b==0){
s=b;
while(a%s==0){
s2=s;
s*=s;
}
a/=s2;
}
if(a<b){
if(c>=b-a){
c-=b-a;
}else{
cout<<a+c<<endl;
bo=0;
break;
}
if(c==0){
cout<<'1'<<endl;
bo=0;
break;
}
cout<<c%(b-1)+1<<endl;
bo=0;
break;
}
//if(bo) cout<<a<<endl;
//else break;
}
if(bo) cout<<a<<endl;
}
return 0;
}

关键在组合数的拆分和前缀和处理以及取模的问题。
#include<bits/stdc++.h>
#define ll long long
#define max_int 2147483647
#define max_ll 9223372036854775807
using namespace std;
vector<vector<int>>q(2001,vector<int>(2001));
vector<vector<int>>p(2001,vector<int>(2001));
void solve(int k){
q[1][1]=1;
for(int i=0;i<=2000;++i){
q[i][0]=1;
}
for(int i=2;i<=2000;i++){
for(int j=1;j<=i;j++){
q[i][j]=(q[i-1][j]+q[i-1][j-1])%k;
}
}
for(int i=2;i<=2000;i++){
for(int j=1;j<=i;j++){
p[i][j]=p[i-1][j]+p[i][j-1]-p[i-1][j-1];
if(q[i][j]==0) p[i][j]+=1;
}
p[i][i+1]=p[i][i];
}
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(0);
int t,k,n,m;
cin>>t>>k;
solve(k);
for(int i=0;i<t;++i){
cin>>n>>m;
if(m>n) m=n;
cout<<p[n][m]<<endl;
}
return 0;
}