横截面数据回归

一些笔记

观测值一定要比参数值多
p值<0.05,拒绝H0.
参数显著，不能说明模型对
AIC与BIC准则，越小越好的指标值AIC
回归分析一定要进行残差的正态性检验。所有的残差都大于0，小于0，都不正常。残差正常应该是分布在0的附近，有正有负，它应该是随机的
残差的正态性检验：检验统计量，是否复合正态分布，QQ图检验正态性
经验分布函数与生存分析函数是相反的
多重共线性：
1.判断是否存在多重共线性VIF>10即存在多重共线性

实验

公路一氧化碳数据

数据：

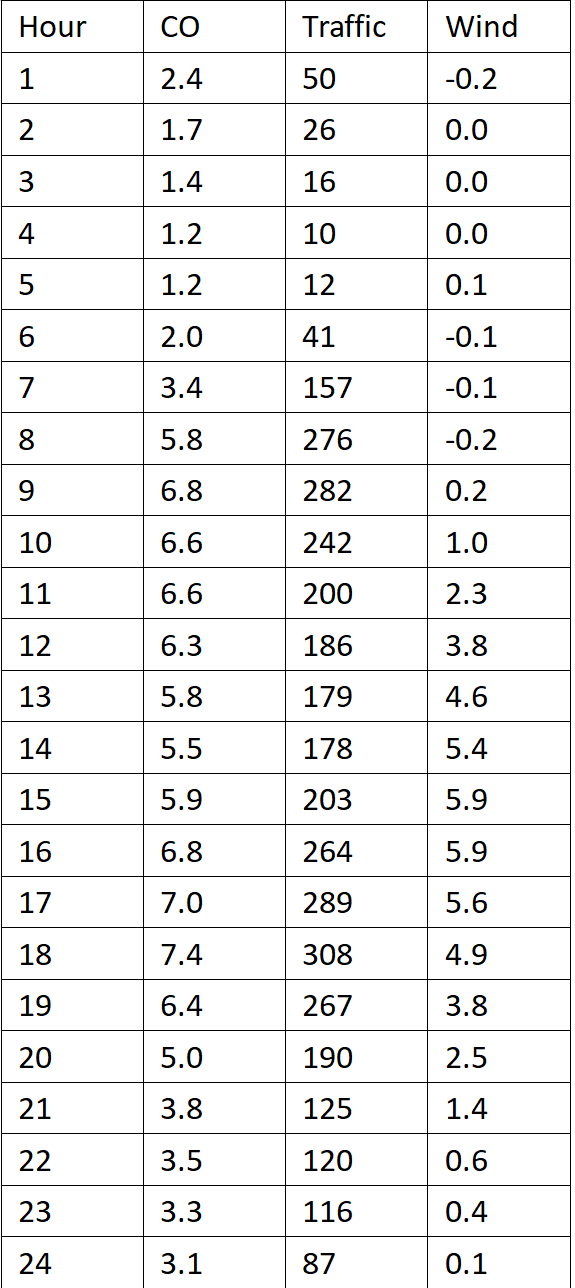
先进行一般的回归，假定残差服从正态分布，也是最简单的线性回归，我们先拟合看一看效果怎么样。
$CO={\beta }_0+{\beta }_{1}Hour+{\beta }_{2}Traffic+{\beta }_{3}Wind+\epsilon$
以最小二乘法拟合，得到参数估计值
代码：

w <- read.table("D:/cofreewy.txt",header = TRUE)
head(w)
a=lm(CO~.,w)#利用3个自变量做线性回归
summary(a)#展示结果
b=step(a,direction="backward")#逐步回归
summary(b)#展示逐步回归结果

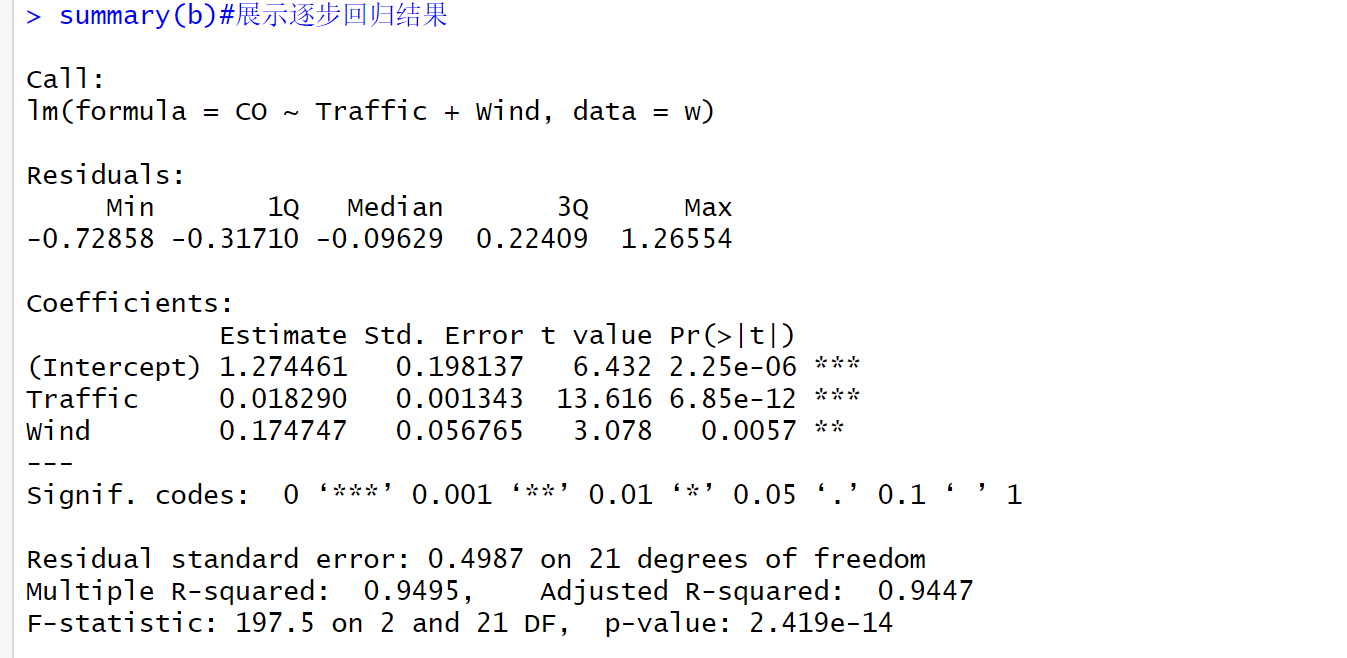
由此可以看出，我们拟合的模型是：
$CO=1.274+0.018\ast Traffic+0.175\ast Wind$
由此可以看出，我们拟合的模型是：
$CO=1.274+0.018\ast Traffic+0.175\ast Wind$

• $R^2$表示线性回归模型中自变量X解释的响应变量y的变化比例.
• $R^2$越大，说明自变量X对响应变量y的解释越强.

这个模型在统计意义上已经不能说明模型对，因为残差是否满足正态分布，我们还不知道，毕竟回归的前提是假设残差满足正态分布。
我们再来看一下残差的分布情况，看看它是否服从正态分布。

shapiro.test(b$res)#做残差的正态性检验

我们可以看出p值>0.05，不拒绝原假设（注意：不是接受原假设，是不拒绝原假设），我们可以假设残差服从正态分布。
但这样是不是就好了，这就是最好的模型呢？

qqnorm(b$res);qqline(b$res)#做残差的QQ图.

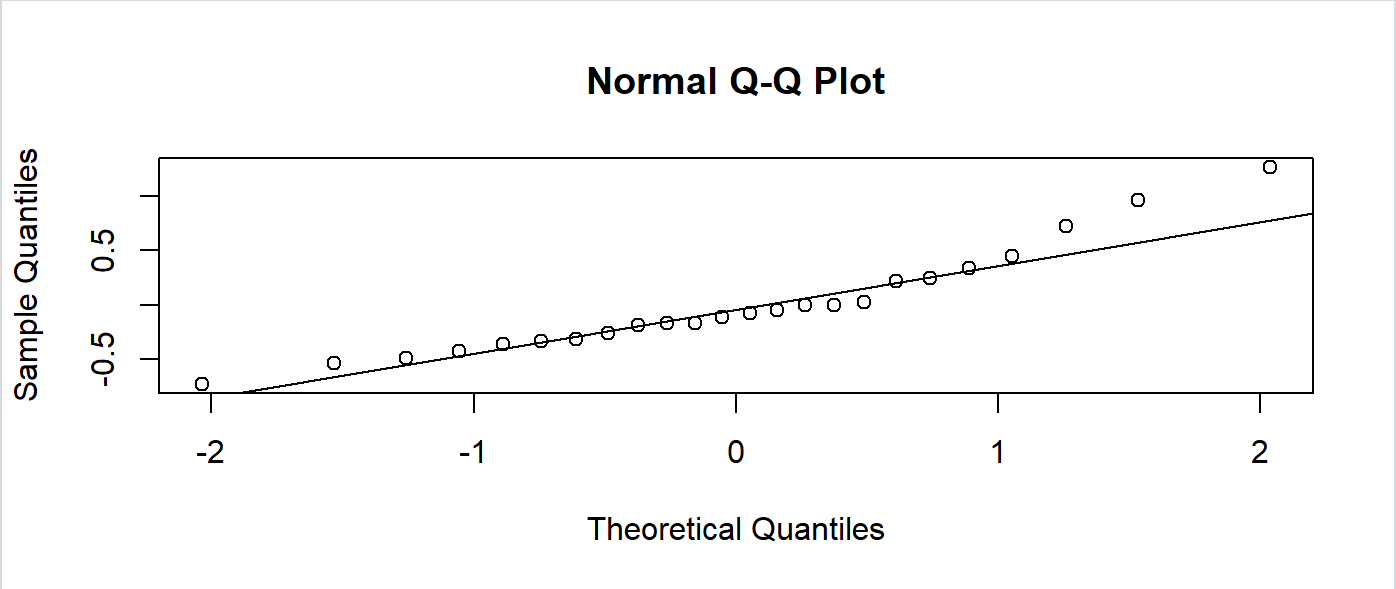
这种线性回归，首先是假定了它的残差是服从正态分布，模型建出来之后，通过QQ图检验它的残差是否真的服从正态分布，那如图所示，如果没有很好的服从或者渐进服从正态呢？怎么办？

注意：在小样本情况下p值0.05的界限不能完全诠释模型优劣
重新拟合，不用线性，用非线性

在此之前让我们先看一看各个属性之间的关系是什么，绘制散点图看一看。

attach(w) #把变量名字放入内存
par(mfrow=c(2,3)) #建立6个图的摆放模式
plot(CO~Traffic);plot(CO~Hour);plot(CO~Wind)
plot(Traffic~Hour);plot(Wind~Hour);plot(Traffic~Wind)
# 也可以直接plot(w)，用一行代码直接绘制所有属性的关系。

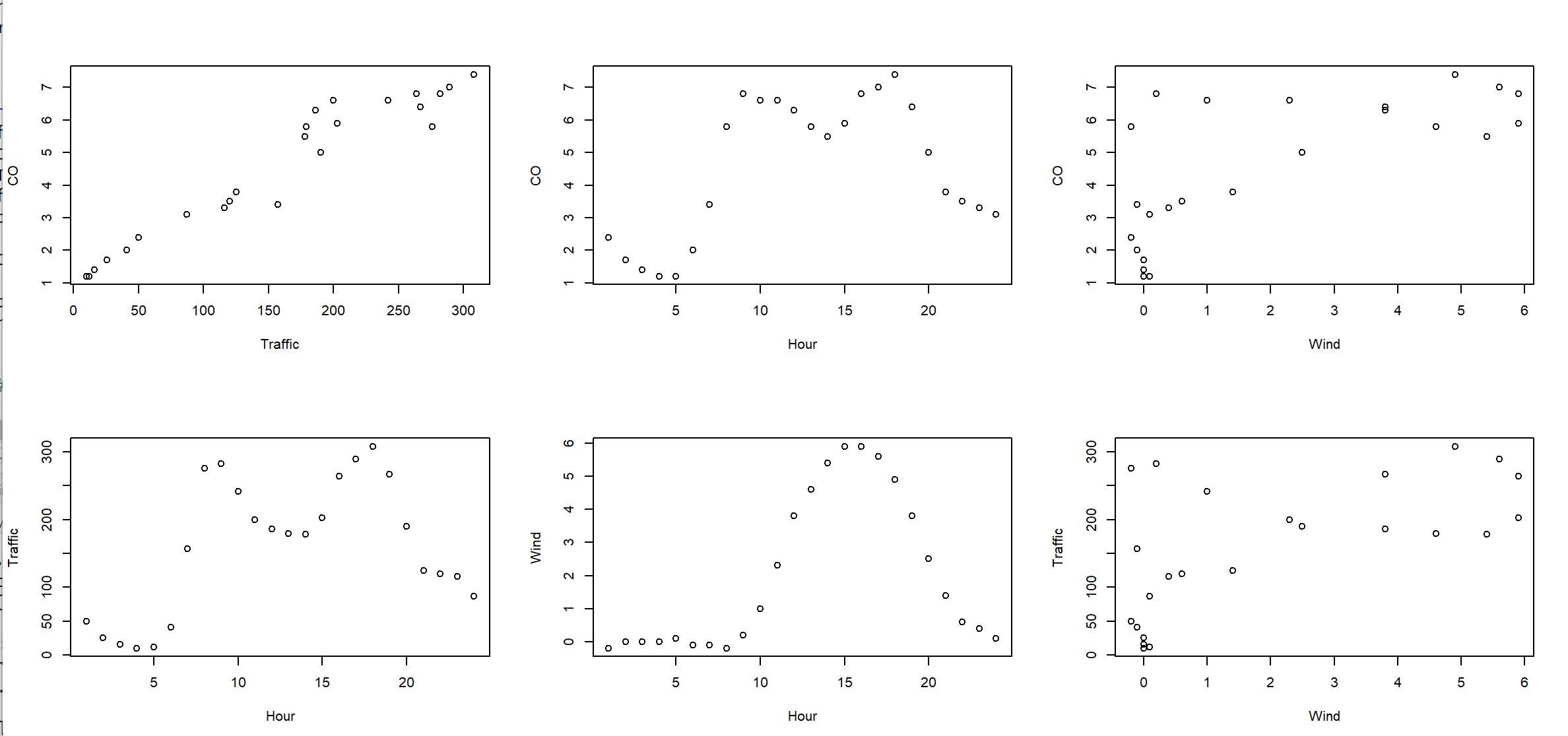
这样就很清楚了，那两个变量之间需要线性关系，那两个之间需要非线性关系，一目了然。
我们可以清晰的看到线性、三角函数，那那个既非线性又非三角函数的周期函数呢？用傅里叶级数。

法国数学家傅里叶认为，任何周期函数都可以用正弦函数和余弦函数构成的无穷级数来表示（选择正弦函数与余弦函数作为基函数是因为它们是正交的），后世称傅里叶级数为一种特殊的三角级数，根据欧拉公式，三角函数又能化成指数形式，也称傅立叶级数为一种指数级数。

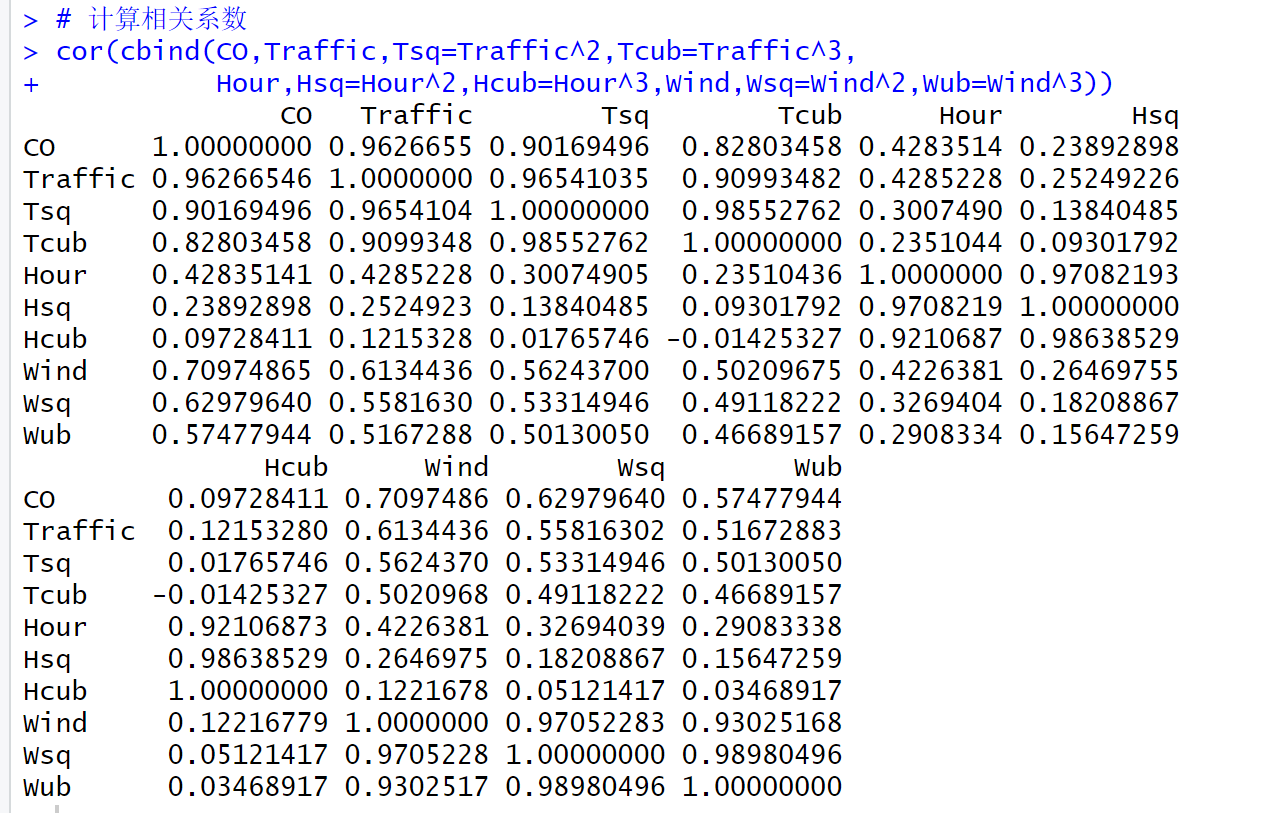
# 计算相关系数
cor(cbind(CO,Traffic,Tsq=Traffic^2,Tcub=Traffic^3,
          Hour,Hsq=Hour^2,Hcub=Hour^3,Wind,Wsq=Wind^2,Wub=Wind^3))

注：cbind()函数是R语言中用于合并数据框的函数，它可以将多个数据框按照列合并。

# 回归
lm2 <- lm(CO~Traffic+Wind+I(Wind^2)+I(Wind^3)+sin((2*pi/24)*Hour)+
            cos((2*pi/24)*Hour)+sin((4*pi/24)*Hour)+cos((4*pi/24)*Hour))
summary(lm2)
lm3<- step(lm2)
summary(lm3)
anova(lm3)
shapiro.test(lm3$res)

# 去掉不显著的重新拟合
lm4 <- lm(CO~Traffic+Wind+I(Wind^2)+
            cos((2*pi/24)*Hour)+cos((4*pi/24)*Hour))
summary(lm4)
anova(lm4)
shapiro.test(lm4$res)
qqnorm(lm4$res)
qqline(lm4$res)

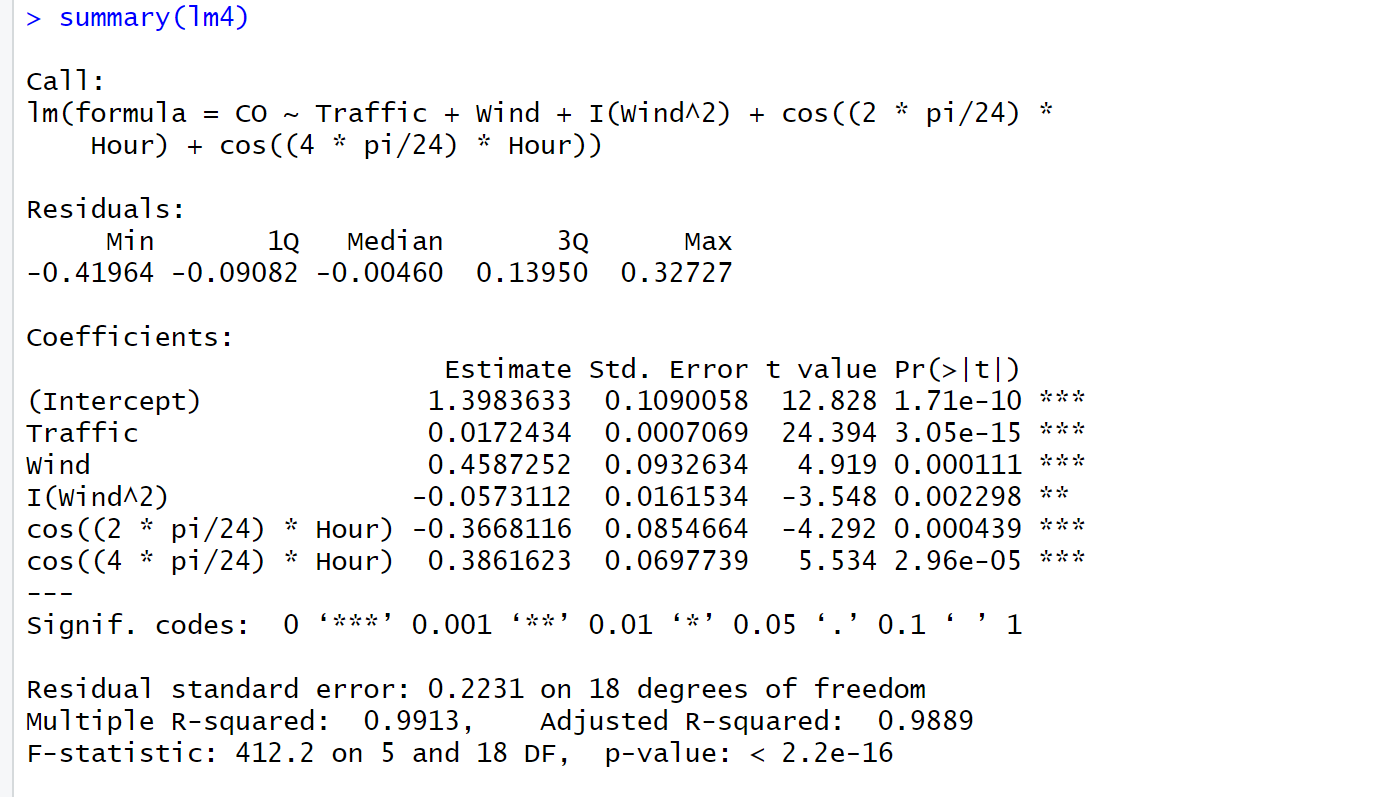
最后的拟合模型为：
$CO=1.38+0.017\ast Traffic+0.459\ast Wind-0.057Win{d}^2-0.366cos((\frac{2\ast pi}{24})\ast Hour)+0.38cos((\frac{4\ast pi}{24})\ast Hour)+\epsilon$

注：其中$\epsilon$表示残差，即$C{O}_i-{\widehat{CO}}_i$
注意$R^2$，此模型要更好

---

总结：

1. 线性回归模型中，如果残差服从正态分布，则可以认为模型是合理的。
2. P值不是万能的，好的模型还是要不断试一试才能出来。
3. 回归是否有意义，还是要放在实际背景中去看