第8章 共形映射(Conformal Mappings)
The results I found for polygons can be extended under
very general assumptions. I have undertaken this
research because it is a step towards a deeper understanding
of the mapping problem, for which not
much has happened since Riemann’s inaugural dissertation;
this, even though the theory of mappings, with
its close connection with the fundamental theorems of
Riemann’s function theory, deserves in the highest degree
to be developed further
(我发现的多边形结果可以在非常一般的假设下进行扩展。 我进行这项研究是因为这是朝着更深入地理解映射问题迈出的一步,自Riemann的第一篇论文发表以来,这方面的工作还没有发生太多。尽管映射理论与Riemann函数理论的基本定理密切相关,但仍值得进一步发展。)
----------------------------------------------------------------------------------------------------E. B. Christoffel,1870
我们在本章中提出的问题和思想在本质上比我们迄今为止看到的问题和思想更具几何特性(geometric)。事实上,在这里我们主要对全纯函数的映射属性感兴趣。特别是,我们的大多数结果将是“全局的”,而不是前三章中证明的更“局部”的分析结果。我们大部分陈述背后的动机在于回答以下简单的问题:
已知 ℂ中两个开集 U 和 V ,则在它们之间存在一个双射吗?
按照全纯双射的概念,我们只是简单地指一个概是全纯又是双射的函数。(将会证明,这个逆向映射自动地就是一个全纯函数。) 这个问题的一个解允许关于解析函数的问题从一个几乎没有几何特性的开集转移到另一个可能具有更多有用属性的开集。主要的例子在于取V = 𝔻 这个单位圆盘,其中很多思想已经发展成研究解析函数(注:对于对应的问题,当 V = ℂ 时,其解是平凡的:只有 U = ℂ 是可能的。见第3章练习14)。事实上,由于圆盘似乎是对 V 的最成熟的选择,因此我们被引向了上述问题的一个变体:
已知 ℂ 的一个开子集 Ω 。在 Ω 上施加什么条件才可以确保从 Ω 到 𝔻 存在一个全纯的双射?
在某些情况下,当双射存在时,它可以通过显式公式给出,我们首先转向理论的这一方面。例如,上半平面可以通过全纯双射映射到圆盘,并且这是通过分式线性变换给出的。从那里,我们可以通过组合之前遇到的简单映射来构造许多其他示例,例如比率函数(rational functions)、三角函数、对数等。作为一种应用,我们讨论某些特定领域的Laplace算子(Laplacian)的 Dirichlet 问题解的这些结构的结果。
接下来,我们通过具体例子来证明本章的第一个一般结果,即 Schwarz 引理,并立即应用于确定所有全纯双射(圆盘对其自身的“自同构(automorphisms)”)。这些再次由分式线性变换给出。
接下来是问题的核心:Riemann 映射定理,该定理指出只要 Ω 是简单连通的,就可以映射到单位圆盘(而不是整个 ℂ )。这是一个值得注意的定理,因为关于 Ω 的假设很少,甚至其边界 ∂Ω 的规律性的假设也没有。(毕竟,圆盘的边界是平滑的。) 特别是,三角形、正方形以及实际上任何多边形的内部都可以通过双射全纯函数映射到圆盘。本章最后一节将详细描述多边形情况下的映射,称为 Schwarz-Christoffel 公式。有趣的是,矩形的映射函数是由“椭圆积分”给出的,这导致了双周期函数。后者是下一章的主题。
1. 共形(保形)等价和示例(Conformal equivalence and examples)
我们首先固定一些在本章余下部分会用到的一些术语。我们称一个双射全纯函数 f :U ⟶ V 为一个共形映射(conformal map)或双同态(biholomorphism)。已知这样一个映射f ,我们称 U 和 V是共形等价的(conformally equavalent)或者简称双全纯的(biholomorphic)。一个重要的事实是,f 的逆则自动成为全纯函数。
命题 1.1 若 f :U ⟶ V 是一个全纯且双射的映射,则对于任意 z ∈ U ,
。特别是,定义于其域上的 f 的逆也是全纯的,因此,一个共形映射的逆也是全纯的。
证明:
我们按反证法论证,假设对于某个 ,
。则
( 对于
附近的任意 z ) ,
其中,a ≠ 0 ,k ≥ 2 且 G 在 处对于 k + 1 阶消没。对于足够小的 w,我们写成
( 其中,
) 。
由于在以 为圆心的小圆上 | G(z)| < | F(z)| ,且 F 在圆内至少有 2 个零点,Rouché定理表明,
在那个圆内至少有2个零点。由于对于任意
但足够接近
有
,这可推导出
的根是不同的,因此,f 不是双射的,这与假设矛盾。
现在令 表示 f 在其范围内的逆(我们假设这个范围是V ),假设
且 w 接近
。记为
和
。若
, 我们有
。
由于 ,我们可以令
从而推导出 g 在
是全纯的,且
。
从这个命题我们推断出,对于两个开集 U 和 V ,当且仅当存在全纯函数 f :U ⟶ V 和 g : V ⟶ U ,使得对于任意 z ∈ U 和 w ∈ V ,g ( f (z) ) = z 和 f (g(w)) = w 成立时,则这两个开集是共形等价的。
我们需要指的是,这里采用的术语不是通用的。某些作者称,对于任意 z ∈ U ,若 ,则全纯映射 f :U ⟶ V 是共形的。这个定义显然没有我们的定义严格;例如,
在穿孔圆盘 ℂ – {0} 满足
, 但却不是双射的。然而,
这个条件等同于(is tantamount to) f 是一个局部的双射(练习1)。存在条件
的一个几何结果,这是定义中术语差异(discrepency)的根源。满足这个条件的一个全纯映射保留角度(不变)。大致说来,若两条件曲线 γ 和 η 相交于
点,α 是这些曲线的切向量之间的定向角,则其像曲线 f ° γ 和 f ° η 相交于
, 则它们的切线向量构成了同样大小的角度 α。问题 2 发展了这种思想。
通过考察几个例子来开启我们对共形映射的研究之旅。首先给出单位圆盘和上半平面之间的共形等价关系,其在很多问题中都起着重要作用。
1.1 圆盘和上半平面(The disc and upper half-plane)
上半平面(我们用 ℍ 表示)由那些具有正的虚数部分的复数构成;即,
ℍ = { z∈ℂ :Im(z)> 0 } 。
一个显著的事实是(第一眼看起来似乎令人震惊),无界结合 ℍ 与单位圆盘是等价的。此外,存在给出这种等价关系的显式公式。事实上,令
和
。
定理 1.2 映射 F : ℍ ⟶ 𝔻 是一个具有逆映射 G : 𝔻 ⟶ ℍ 的共形映射。
证明:
首先我们观察到,这两个映射在其各自的域中都是全纯的。则我们注意到,上半平面中的任意点相比–i 都更加接加 i ,因此,| F(z)| < 1 且 F 映射 ℍ 到 𝔻 。为了证明 G 将 𝔻 映射到上关平面 ℍ ,我们必须计算 Im(G (w))(对于 w∈𝔻) 。为此目的,我们令 w = u + iv , 并注意
(因为 |w| < 1)。
因此,G 映射单位圆盘到上半平面。
最后,
,
类似地,G(F (z)) = z 。这就证明了这个定理。
这些函数的另一个有趣的方面是它们在我们的开集边界上的行为(注:共形映射的边界行为在本章中起着重要作用,将会反复出现)。我们观察到,F 在 ℂ 上处处全纯(除了在 z = -i 点处),特别是,其在 ℍ 的边界上(即,在实线上)处处连续。若我们取 z = x 为实数,则从 x 到 i 的距离等于从 x 到 –i 的距离,因此,| F (x)| = 1 。因此,F 映射 ℝ 到 𝔻 的边界上。我们通过将F (x) 写成
而获得了更多的信息,并使用 对实线进行参数化。由于
和
,
我们有 (译注:根据 Euler 公式)。因此,实线的像是由圆略去点 -1 构成的弧。此外,随着 x 从 -∞ 移动到 +∞ ,F(x)沿着以 -1 为起点的弧移动并且首先穿过圆的位于下半面平的这部分。
圆上的点 -1 对应上半平面的“无穷远处的点”。
评注:
形如
(其中,a, b, c, 和 d 是复数,并假设分母不是分子的倍数)
的映射通常被称为分式线性变换(fractional linear transformations)。其他例子是定理 2.1 和 2.4 中圆盘和上半平面的自同构。
1.2 更多例子(Further examples)
我们在此收集了几个共形映射的实例。在某些情况下,我们讨论相关域的边界上的映射行业。其中的一些映射如图 1 所示。
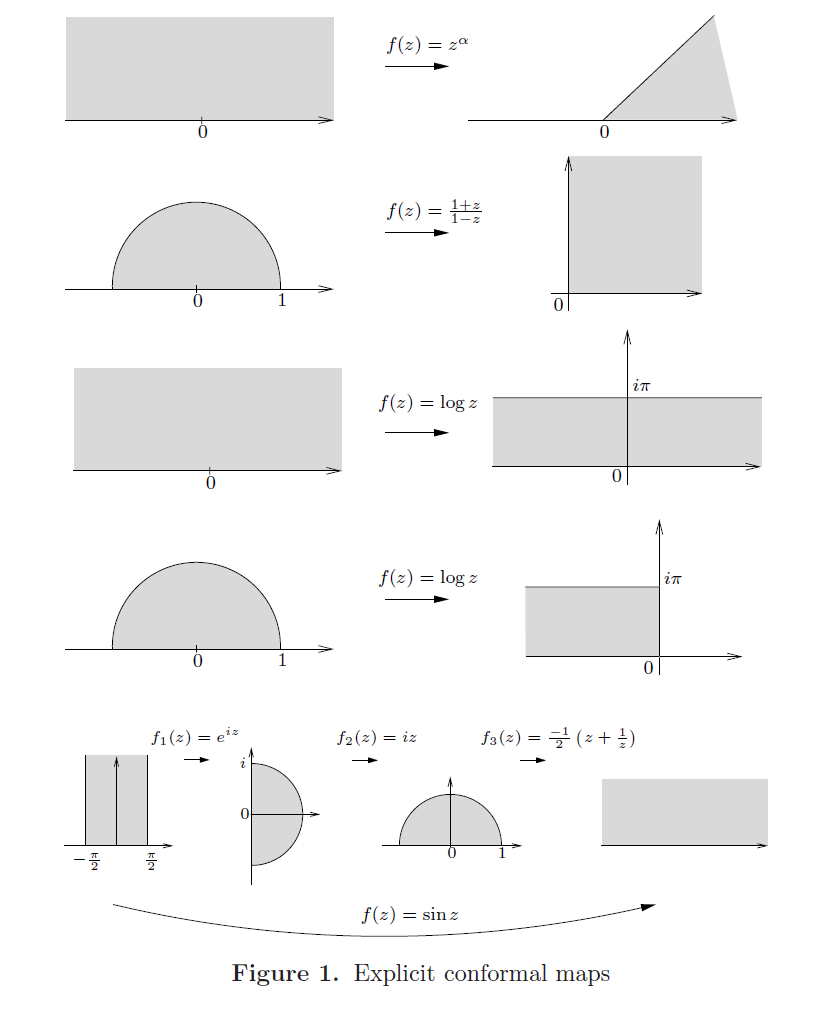
-------------------------------------------------图 1: 显式共形映射--------------------------------------------------
例子 1:
平移和膨胀(dilations)提供了第一个简单的例子。事实上,若 h∈ℂ ,平移 z ⟼ z + h 是一个从 ℂ 到其自身的共形映射,其逆是 w ⟼ w – h 。若 h 是实数,则这个平移也是一个从上半平面到其自身的共形映射。
对于任意非零复数 c ,映射 f : z ⟼ cz 是从复平面到其自身的共形映射,其逆是简单的 。若 c 具有模 1 ,且使得对于某个实数 φ ,有
,则 f 是一个按 φ 弧度执行的旋转(rotation)。若 c > 0 ,则 f 对应一个膨胀。最后,若 c < 0 ,则映射 f 由|c|后接一个 π 的旋转的膨胀构成。
例子 2:
若 n 是一个正整数。则映射 是一个从扇形
到上半平面的共形映射。这个映射的逆只是简单的
(根据对数主支的定义)。
更一般地,若 0 < α < 2 , 则映射 将上半平面映射到(译注:take ... to ...在这里应当是指映射)扇形
。事实上,若我们选择通过删除正实轴(的对数部分)而获得的对数分支,以及选择
(r > 0 且 0 < θ < π ),则
。
因此,f 映射 ℍ 到 S 。此外,一个简单的验证可证明,f 的逆可由 得到,其中,被选择的对数分支使得
。
通过将刚刚讨论的映射与前面示例中的平移和旋转组合起来,我们可以将上半平面共形地映射到 ℂ 中任意(无穷的)扇形。
让我们指出 f 的边界行为。若 x 在实线上由 -∞ 移动到 0 。则 f (x) 在由 所确定的半轴上从
移动到 0 。随着 x 在实线上由 0 趋近于 ∞ ,其像 f(x) 也在实线上由 0 趋近于 ∞ 。
例子 3:
映射 f(z) = (1 - z)/(1 + z) 将上半圆盘 { z = x + iy: |z|< 1 且 y > 0 } 保形地映射到第一象限 { w = u + iv: u > 0 且 v > 0 }。事实上,若 z = x + iy 我们有
,
因此,f 将上半平面中的半圆盘映射到第一象限。其逆映射(由 g(z) = (w - 1)/(w + 1))在第一象限很显然也是全纯的。此外,对于第一象限中的任意 w ,| w + 1|>| w - 1| ,因为从 w 到 -1 的距离大于从 w 到 1 的距离;因为 g 映射到单位圆盘。最后,简单计算可证明,只要 w 在第一象限, 则 g(w)的虚数部分是正的。因此,g 将第一象限转换到预期的半圆盘,则我们推断出 f 是共形的,因为 g 是 f 的逆。
为了检查 f 在边界上的行为,注意到,若 属于上半圆,则
。
随着 θ 从 0 移动到 π ,我们发现 沿着虚轴从无穷大移动到 0 。此外,若 z = x 是实数,则
也是实数;我们从这一点可以看到,f 事实是一个从(-1,1)到正实轴的双射,且当 x 从 -1 移动到 1 时,f(x)从 0 增长到无穷大。此外注意 f (0) = 1 。
例子 4:
映射 ,定义为删除掉负虚轴部分后而获得的对数分支,将上半平面映射到带域 {w = u + iv :u∈ℝ ,0 < v < π }。从以下事实立即可推导出这一结果——若
(r > 0 且 –π/2 < θ < 3π/2 ),则根据定义,
。
其相反的映射则是 。
当 x 从 -∞ 移动到 0 的时候,点 f (x) 在直线{ x + iπ : -∞ < v < ∞} 上从 ∞+ iπ 移动到 -∞ + iπ 。当 x 在实线上从 0 移动到 ∞ 时,其象 f (x)则沿着实线从-∞ 移动到 ∞ 。
例子 5:
通过对前面例子的思考,我们发现, 也定义了一个从半圆盘 { z = x + iy: |z|< 1 且 y > 0 } 到半带域 {w = u + iv :u < 0 ,0 < v < π}的一个共形映射。随着 x 在实线上从 -∞ 移动到 0,则
从 -∞ 移动 0 。当 x 在上半平面的半圆中从从 -1 移动 1 的过程中,则点
在带域的垂直线段上从 0 移动 πi 。最后,随着 x 从 -1 移动 0 ,点
在带域的上半直线从 iπ 移动到 -∞ + πi 。
例子 6:
将半带域 {z = x + iy :–π/2 < x < π/2 , y > 0} 共形地映射到半圆盘 { w = u + iv: |w|< 1 且 u > 0 }。这一点可从以下事实立即推导出——若 z = x + iy 则
。
若 x 从 π/2 + i∞ 移动到 π/2 ,则 f (x)从 0 移动到 i ,而随着 x 从 π/2 移动到 -π/2 ,则 f (x)在半圆上从 i 移动到 - i 。最后,随着 x 从 -π/2 移动到 -π/2 + i∞ ,我们发现,f (x) 从 - i 移回到 0 。
映射 f 与例子 5 中的映射的逆密切相关。
例子 7:
函数 是一个从半圆盘 { z = x + iy :|z| < 1, y > 0} 到上半平面的共形映射(练习5)。
f 的边界行为如下:某 x 从 0 移动 1 ,则 f (x)在实线上从 ∞ 移动到 1 。若 ,则
且随着 x 在上半平面沿着单位半圆从 1 移动 -1 ,则 f (x) 在实线段上从 1 移动 -1 。最后,当 x 从 -1 移动 0 时,则 f (x)沿着实线从 -1 移动到 -∞ 。
例子 8:
映射 将上半平面共形地映射到半带域 {w = x + iy : –π/2 < x < π/2 , y > 0 } 。为了理解这一点,注意到,若
,则
,
因此,首先通过应用例 6 中的映射获得 f ,然后再乘以 i (即,旋转 π/2),最后,应用例7中的映射。
随着 x 从 –π/2 + i∞ 移动到 –π/2,则点 f (x) 从 -∞ 移动到 -1 。当 x 是介于 –π/2 与 π/2 之间的实数时,则 f (x) 也是介于 -1 到 1 之间的实数。最后,若 x 从 π/2 移动到 π/2 + i∞ ,则 f (x) 在实线上从 1 移动到 ∞ 。
1.3 带域中的Dirichlet问题(The Dirichlet problem in a strip)
开集 Ω 中的 Dirichlet 问题包括求解

,其中,Δ 表示 Laplace 算子 ,且 f 是一个 Ω 的边界上已知的函数。换句话说,我们希望求得一个 Ω 中的具有所描述的边界值 f 的调和函数。这个问题已经在第 I 册书中在 Ω 是单位圆盘或者上半平面的情况下考虑过,其中,它是在稳态热传导方程的解中出现的。在这些具体示例中,通过与 Poisson 核的卷积获得了显式解。
我们的目标是将 Dirichlet 问题与迄今为止讨论的共形映射联系起来。我们首先提供一个在 Ω 是带域的特殊情况下问题(1)的求解公式。事实上,这个例子在第 I 册书第 5 章的问题 3 中进行了研究,该问题是使用 Fourier 变换解决的。在这里,我们仅使用保形(共形)映射和圆盘中的已知解来恢复该解。
我们使用的第一个重要事实是,调和函数与全纯函数的复合仍然是调和函数。
引理 1.3 令 V 和 U 为 ℂ 中的开集,且 F : V ⟶ U 是一个全纯函数。若 u: U ⟶ ℂ 是一个调和函数,则 u ° F 是 V 上的一个调和函数。
证明:
引理的主旨(thrust)纯粹是局部的,因此,我们可以假设 U 是一个开圆盘。我们令 G 为 U (其实部为 u )(根据第2章练习12,这样的一个 G 是存在的,最多取决于一个附加常数)中的一个全纯函数。令 并注意到,
是 H 的实部。因此,
是一个调和函数,因为 H 是全纯的。
这个引理的另一种(计算的)证明参见练习 6 。
具备这样的结果之后,现在我们可以考虑当 Ω 由水平带域
Ω ={ x + iy : x∈ℝ ,0 < y < 1 } (其边界是两条水平直线 ℝ 和 i + ℝ 的并集)
构成时的问题(1)。我们将边界数据表述为定义于 ℝ 上的两个函数 和
。并寻求 Δu = 0 的 Ω 中的解 u (x,y),其满足
且
。
我们假设 和
连续且在无穷远处消没,即,
(对于 j = 1 , 2)。
我们将遵循的方法包括通过共形映射将问题从带域重新定位到单位圆盘。在这个圆盘中解 则按与Poisson核的一个卷积进行表述。最后,使用前面提到的共形映射将
移回到带域,由此给到了我们这个问题的答案。
为了实现我们的目标,我们引入了映射 F : 𝔻 ⟶ Ω 和 G : Ω⟶𝔻 ,分别定义为
和
。
这两个函数(由来自于前面章节中的例子的组合映射而获得)是共形且互逆的。
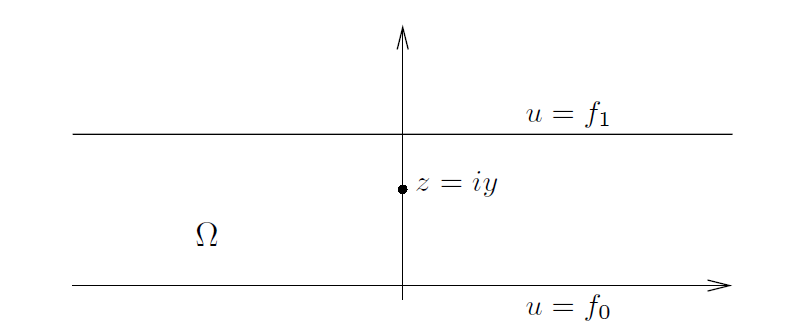
--------------------------------------------图2: 带域中的Dirichlet问题----------------------------------------------
通过追踪 F 的边界行为,我们发现,它将下半圆映射到直线 i + ℝ,以及将上半圆映射到 ℝ 。更确切地说,随着 φ 从 –π 移动到 0 ,则 从 i + ∞ 移动到 i -∞ ,而随着 φ 从 0 移动到 π ,则
在实线上从 -∞ 移动到 ∞ 。
在认识了 F 在圆上的行为之后,我们定义
( 只要 –π < φ < 0 )
和
( 只要 0 < φ < π )。
则,由于 和
在无穷远处消没,函数
在下半圆上等于函数
,在上半圆等于
,并且 0 值位于点 φ = ±π ,0 ,且
在整个圆上是连续的。在单位圆盘上具有边界数据
Dirichlet 问题解由 Poisson 积分(注:我们建议读者参见第 I 册书的第 2 章,详细讨论圆盘中的 Dirichlet 问题和 Poisson 积分公式部分的知识。另外,Poisson积分公式在本书第 2 章练习 12 和第 3 章问题 2 中得到推导。)
给出,其中 ,而
是 Poisson 核。引理 1.3 确保了函数 u (定义为 ) 在带域上是一个调和函数。此外,我们的构造也确保了函数 u 具有正确的边界值。
首先在点 z = iy 处获得 和
所表示的 u 的公式(其中 0 < y < 1)。合适的变量替换(见练习7)表明,若
,则
。
类似的计算也建立了下列公式
。
最后两个公式加在一起就提供了 u(0,y)的一个公式。通常(回顾第I册第5章练习13),消没于无穷远处的带域中的 Dirichlet 问题的解是唯一的。接下来,边界条件平移 x 导致其解也平移 x 。因此,我们可以应用相同的论证到 和
(固定x ),最后的变量替换证明
,
这就得到了带域中 Dirichlet 问题的一个解。特别是,我们求得的这个解是根据与函数 和
的卷积给出的。此外,注意到,在带域的中间点(y = 1/2) , 其解是由对函数
的积分给出的;这个函数碰巧是其自身的 Fourier 变换,正如第 3 章例子 3 所示。
关于Dirichlet问题的评注(Remarks about the Dirichlet problem)
上述例子引导我们设想了(envisage)针对 Ω (一个合适的区域)的更一般的 Dirichlet 问题的解(若我们知道一个从圆盘到 Ω 的共形映射 F )。即,假设我们想求解(1),其中,f 是指定的连续函数,而 ∂Ω 是 Ω 的边界。假设我们已有一个从 𝔻 到 Ω 的共形映射(即,扩展为一个圆盘的边界到 Ω 的边界的连续的双射)。然后, ◦ F 定义于圆上,则我们可以针对具有边界数据
的圆盘求解 Dirichlet 问题。其解由 Poisson 积分公式
给出,其中, 是 Poisson 核。则,我们可以指望源问题的解由
给出。
这种方法的成功要求我们能够肯定地解决两个问题:
存在一个从 Ω 到 𝔻 的共形映射
吗?
如果存在,那么这个映射从 Ω 的边界到 𝔻 的边界扩展了一个连续的双射吗?
第一个问题(存在性问题)可通过 Riemann 映射定理(我们将在下一节证明它)解决。它是完全通用的(仅假设 Ω 是简单连通域 ℂ 的真子集(proper subset)),并且不需要 Ω 边界具有规律性。第二个问题的一个肯定的答案是要求 ∂Ω 的某种规律性。一种特别的情况(当 Ω 在多边形内部时)在下述 4.3 节处理。(更多通用结论参见练习 18 和 问题 6。)
有趣的是,注意到,在 Riemann 解决映射问题的最初方法中,其含义链是相反的:他的思想是,从 Ω 到 𝔻 的共形映射 𝛟 是一个 Ω 中 Dirichlet 问题的可解(solvability)的结果(consequence)。他按后述方式进行论证。假设我们希望求得这样一个 𝛟 ,其有一个属性是将一个已知点 映射到 0。则 𝛟 一定具有形式
,
其中,是全纯的且在 Ω 中非消没。因此,我们可以取
(对于合适的 H(z) )。
现在,若 u(z)是由 u = Re(H) 给出调和函数,则 ∂Ω 上 | 𝛟(z)| = 1 这个事实意味着 u 一定边界条件 (对于 z ∈∂Ω )。因此,若我们可以求得 Dirichlet 问题的这样一个解 u (注:调和函数 u(z) 也称为对于域 Ω 具有源点
的Green 函数),则我们就可以构造 H ,并由此构造映射函数 𝛟。
然而,这种方法有几个缺点。首先,我们必须验证 𝛟 是双射的。此外,要继续进行的话,这种方法还要求 Ω 的边界具有某种规律性。其次,我们仍然面对求解 Ω 的Dirichlet 问题。在这一阶段,Riemann提出使用“Dirichlet原理”。但应用这一思想涉及到必须克服的困难(注:Dirichlet原理在当前二维情况下的实现在第 III 册中进行了介绍)。
然而,使用不同的方法,我们可以在一般情况下证明映射的存在。以下第 3 节介绍了这种方法。
2. Schwarz引理;圆盘和上半平面的自同构 (The Schwarz lemma; automorphisms of the disc and upper half-plane)
Schwarz引理的证明和证明均简单,但这个结论的应用却是深远的(far-reaching)。我们回顾一下,一个旋转就是一个形如 z ⟼ cz 且 |c| = 1 的映射,即, (其中,θ∈ℝ 被称为旋转角且定义明确,最多为 2π 的整数倍)。
引理 2.1 令 f : 𝔻 ⟶ 𝔻 一个全纯函数且 f(0) = 0 。则
(i) 对于任意 z∈𝔻 有 | f(z)| ≤ |z | 。
(ii) 若对于某个 , 我们有
, 则 f 是一个旋转。
(iii) ,且若等号成立,则 f 是一个旋转。
证明:
我们首先按以 0 为中心且在整个 𝔻 上收敛的幂级数展开 f ,即
。
因为 f(0) = 0 ,所以我们 ,故而 f (z)/ z 是 𝔻 中的全纯函数(因为它在 0 处有一个可除奇点)。若 |z| = r < 1 ,则由于 | f (z)| ≤ 1 我们有
,
根据最大模原理,我们可以推断出只要 |z| ≤ r ,以上不等式是成立的。则令 r ⟶ 1 我们得到了第一个结果。
对于(ii),我们看到,f (z)/ z 在 𝔻 的内部获得了其最大值,因此一定是一个常量(比如 f (z) = cz )。在 点估算这个表达式并取绝对值,我们求得 |c| = 1 。因此,存在 θ∈ℝ 使得
,这就解释了为什么 f 是一个旋转。
最后,观察到,若 g (z) = f (z)/ z ,则在整个 𝔻 上有 | g (z)| ≤ 1 ,此外,
。
因此,若 ,则 | g (0)| = 1 ,且根据最大值原理,g 是常量,这意味着 f (z) = cz 且 |c| = 1 。
我们对这个引理的第一个应用是确定圆盘的自同构(automorphisms)。
2.1 圆盘的自同构(Automorphisms of the disk)
我们称从一个开集 Ω 到其自身的共形映射为 Ω 的自同构(automorphisms)。Ω 的所有自同构的集合用 Aut(Ω) 表示,并带有一个群结构。群运算是复合映射,恒等元素是映射 z ⟼ z ,且其逆只是简单的反函数。很显然,若 f 和 g 是 Ω 的自同构,则 也是一个自同构,事实上,其逆由
给出。如上所述,恒等映射总是一个自同构。我们可以给出其它更有趣的单位圆盘的自同构。很显然,任意按角度 θ∈ℝ 进行的旋转(即, ) 是单位圆盘的一个自同构,其逆是按角度 –θ 的一个旋转 (即,
)。更有趣的是形如
(其中,α∈ℂ 且 |α| < 1)
的自同构。这些映射(在第 1 章练习 7 中介绍的那些)出现在复分析的许多问题中,由于它们有很多有用的属性。要证明它们是 𝔻 的自同构也非常简单。首先,观察到,由于 |α| < 1 ,则映射 在单位圆盘中是全纯的。若 |z| = 1 则
以及
(其中,
) ,
因此, 。根据最大模原理,我们推断出对于任意 z∈𝔻 有
。最后我们做以下简单的观察:
,
据此,我们推断出 是其自身的逆!
的另一个重要属性是其在 z = α 处消没;此外,它还交换 0 和 α ,即
和
。
下一个定理指的是,与映射 组合的旋转穷尽圆盘的所有自同构。
定理 2.2 若 f 是圆盘的一个自同构,则存在 θ∈ℝ 和 α∈𝔻 使得
。
证明:
由于 f 是圆盘的一个自同构,则存在一个唯一的复数 α∈𝔻 使得 f (α) = 0 。现在我们考虑定义为 的自同构 g 。则 g (0) = 0 ,由 Schwarz 引理给出
(2) | g (z)| ≤ | z| ( 对于任意 α∈𝔻 ) 。
此外, ,因此,应用 Schwarz 引理于
, 我们求得
( 对于任意 w∈𝔻 ) 。
对于每一个 z∈𝔻 ,对 w = g (z) 使用最后一个不等式,就给出了
(3) | z| ≤ | g (z)| ( 对于任意 z∈𝔻 ) 。
结合 (2) 和 (3) 我们求得 | g (z)| = | z| ( 对于任意 z∈𝔻 ),并根据 Schwarz 引理我们推断出对于某个 θ∈ℝ 有 ,我们推断出
,正如所断言的那样。
在定理中令 α = 0 便产生了下面的结论。
推论 2.3 固定了原点的单位圆盘的唯一自同构是旋转。
注意到,通过使用映射 ,我们可以看到,圆盘的自同构表现得可传递,在已知任意圆盘中的点对 α 和 β 的意义上,存在一个将 α 映射到 β 的自同构 ψ,这样一个自同构 ψ 由
给出。
𝔻 的自同构的显式公式给出了一个群 Aut(𝔻)的很好的描述。事实上,这个自同构的群与具有复条目的 2 × 2 的矩阵群“几乎”是同构的,并用 SU(1,1)表示。这个群由所有 2 × 2 的矩阵构成,这些矩阵在 上保有 hermit形式,并定义为
,
其中, 和
。关于这个主题的更多信息,我们建议读者参阅问题 4 。
2.2 上半平面的自同构(Automorphisms of the upper half-plane)
我们有关 𝔻 的自同构知识,再结合 1.1 节中学习的共形映射 F : ℍ ⟶ 𝔻 知识一起,允许我们确定 ℍ 的自同构群,我们用Aut(ℍ)表示。
考虑映射
Γ : Aut(𝔻) ⟶ Aut(ℍ),
它由“F 的共轭”给出,即
。
很显然,只要 𝜑 是一个 𝔻 的自同构,则 Γ(𝜑) 就是一个 ℍ 的自同构,并且 Γ 还是一个双射,其逆由 给出。事实上,我们可以进一步地证明,Γ 保留了相应自同构群上的运算。诚然,假设
, 由于
在 𝔻 上是恒等的,我们求得
。
结论是,这两个群 Aut(𝔻)和 Aut(ℍ)是相同的,因为 Γ 在它们之间定义了一个自同构。我们还余下的任务是,给出 Aut(ℍ)的元素的表达式。
可以使用一系列的计算(包括通过 F 将圆盘的自同构拉回到上半平面)来验证, Aut(ℍ)由所有映射
,
其中,a , b, c, 和 d 是实数, 且 ad – bc = 1 。再一次,一个矩阵群潜伏(lurk)在背景中。令 所有具有实数条目和行列式 1 的 2 × 2 矩阵群,即
。
我们称这个群为特殊线性群(special linear group)。
已知一个群 , 我们定义映射
为
。
定理 2.4 ℍ 的每一个自同构对某个群 采用
的形式。反之,这种形式的每一个映射都是 ℍ 的一个自同构。
对其的证明包括一系列步聚。为简洁起见,我们用 𝒢 表示群 (译注:𝒢 的Unicode编码:1D4A2,LaTex语法:\mathcal{G})。
第一步:若 M ∈ 𝒢 ,则 将 ℍ 映射到自身。从以下观察
(4) (只要 z∈ℍ )
可以看出,这是显而易见的。
第二步:若 M 和 是 𝒢 中的两个矩阵,则
。这一步可从直接计算推导出,我们忽略。因此,我们可以证明定量的第一部分。每个
都是一个自同构。因为它有一个全纯的逆
(简记为
)。事实上,若 I 是恒等矩阵,则
。
第三步:已经 ℍ 中任意两点 z 和 w,存在 M ∈ 𝒢 使得 ,因此,𝒢 在 ℍ 上表现得具有传递性。为了证明这一点,只需证明我们可以映射任何 z ∈ ℍ 到 i 即可。在以上等式(4)中令 d = 0 得到
,
并且我们可以选择一个实数 c 使得 。接下来,我们选择矩阵
使得 具有等于 1 的虚部。则我们通过一个形如
(b∈ℝ)
的矩阵平移将 映射到 i 。最后, 映射
(具有
) 将 z 映射到 i 。第四步:若 θ 是一个实数,则矩阵
属于 𝒢 ,且若 F : ℍ ⟶ 𝔻 表示标准的共形映射,则 对应圆盘中角度为 -2θ 的旋转。可以从事实
推导出这一点,这不难验证。
第五步:现在我们可以完成对定理的证明。我们假设 f 是 ℍ 的一个自同构且 f (β) = i 。则 满足 g(i) = i ,因此,
是一个固定了原点的圆盘的自同构。因此,
是一个旋转,根据第四步,存在一个 θ∈ℝ 使得
。
因此, ,故而我们可以推断出
具有预期的形式。
最后一个观察是,群 Aut(ℍ)与群 并不是非常同构。原因在于,矩阵 M 和 - M 产生了相同的函数
。因此,若我们认为这两个矩阵 M 和 -M 是一致的,则我们得到了一个新的群
,我们称其为射影特殊线性群(projective special linear group);这个群与群 Aut(ℍ)是同构的。
3. Riemann映射定理 (The Riemann mapping theorem)
3.1 定理的必要条件和表述(Necessary conditions and statement of the theorem)
现在我们来谈谈本章所承诺的基石(cornerstone)。基本问题是确定开集 Ω 上确保共形映射 F : Ω⟶ 𝔻 存在的条件。
一系列简单的考察允许我们求得 Ω 上的必要条件。首先,Ω = ℂ 则不存在共形映射 F : Ω⟶ 𝔻 ,因为根据 Liouville 定理,F 必须是一个常量。因此,一个必要条件是假设 Ω ≠ ℂ 。由于 𝔻 是连通的。我们也必须要求 Ω 是连通的。我们必须还加一个条件:因为 𝔻 是简单连通的,所以 Ω 也必须是简单连通的(参见练习 3 )。很显然,施加在 Ω 上的这些条件也足以保证从 Ω 到 𝔻 的双同态(bihomomorphism)的存在。
为简便起见,如果 ℂ 的一个子集 Ω 非空并且不涵盖整个 ℂ ,则我们将称这个子集是真子集(proper)。
定理 3.1 Riemann 映射定理(Riemann mapping theorem) 假设 Ω 是真子集且是简单连通的。若 ,则存在一个唯一的共形映射 F : Ω⟶ 𝔻 使得
且
。
推论 3.2 在 ℂ 中的任意两个真简单连通开子集是共形等价的。
很显然,这个推论可直接由定理得出,因为我们可以使用单位圆盘作为中间步骤。此外,定理中唯一性的表述是显而易见的,因为,若 F 和 G 是满足这两个条件的从 Ω 到 𝔻 的共形映射,则 是一个固定了原点的圆盘的自同构。因此,
,且由于
,我们一定有
,据此我们推断出 F = G。
本节余下部分专注于共形映射 F 的存在性的证明。证明的思想如后续所述。我们考虑所有双射全纯映射 。我们希望从这些双射映射中选择一个 f,使得其像位于 𝔻 之外,可通过使得
尽可能大来实现这一点。为此,我们需要能够从给定的函数序列中提取 f 作为极限。我们首先讨论这一点。
3.2 Montel定理(Montel’s theorem)
(译注:Paul Antoine Aristide Montel,法国数学家。他研究最多的是关于复分析中全纯函数的内容。)
令 Ω 为 ℂ 的一个开子集。对于 Ω 上的一个全纯函数族 ℱ ,若 ℱ 中的每一个序列都有一个在 Ω 的每一个紧子集上一致收敛的子序列(不必在 ℱ 中有极限),则称 ℱ 是正规的(normal,或称规整的)。
实际上,函数族正规性的证明是两个相关性质应用的结果,即一致有界性和等度连续性(equicontinuity),我们现在来定义这些性质。
对于一个函数族 ℱ ,若对于每一个紧集合 K⊂ Ω 都存在一个 B > 0 ,使得
| f (z)| ≤ B (对于任意 z∈K 和 f∈ℱ),
则我们称 ℱ 在 Ω 的紧子集合上是一致有界的(uniformly bounded on compact subsets of Ω)。
此外,若对于任一个 ε > 0 ,都存在一个 δ > 0 ,使得只要 z ,w∈K 且 | z - w | < δ ,便有
| f (z)- f (w)| < ε (对于任意 f ∈ℱ ) ,
则称函数族 ℱ 是等度连续的(equicontinuous)。等度连续性是一个强条件,要求函数族具有一致连续性(译注:即均匀连续性)。例如,任何在 [0, 1] 上导数一致有界的可微函数族都是等度连续的,这可直接从中值定理推导。在另一方面,注意到 [0, 1]的由 所给出的族
不是等度连续的,因为对于任意因定的
我们有
(当 n 趋近于无穷大时)。
随后的定理将这些新概念整合在一起,成为证明 Riemann 定理的的重要材料。
定理 3.3 假设 ℱ 是 Ω 上的一个全纯函数族,并在 Ω 的紧子集上一致有界。则
(i) ℱ 在 Ω 的每一个紧子集上都是等度连续的。
(ii) ℱ 是一个正规函数族。
这个定理实际上包括两个单独的部分。第一部分指的是,ℱ 在 ℱ 是 Ω 上的一个全纯函数族和在 Ω 的紧子集上一致有界这两个假设的条件之下是等度连续的。可应用 Cauchy 积分公式推导出其证明,因此,对其的证明取决于 ℱ 由全纯函数构成的事实。这个结论与由 所给出的 (0, 1)上的函数族(一致有界)所示的实数情况形成鲜明的对比。然而,这个函数族
不是等度连续的,并且在(0, 1)的任意紧子区间上都没有收敛的子序列。
定理的第二部分在本质上不是复分析的。事实上,ℱ 是正规函数族的事实,可从仅假设 ℱ 一致有界且在 Ω 的紧子集上等度连续而推断出。有时候称这个结论为 Arzela-Ascoli 定理 ,对其的证明主要包括对角化论证(diagonalization argument)。
我们需要证明 Ω 的任意紧子集上的收敛性,因此,引入下面的概念显得非常有用。
对于 Ω 的一个紧子集序列 ,若满足
(a) 含于
的内部(对于所有 𝓁 = 1 ,2 ,....),
(b) 对于某个 𝓁 ,任意紧子集 K⊂ Ω 含于 , 特别是,
,
则我们称这个序列是一个穷举(exhaustion,也称为穷竭或耗尽)。
引理 3.4 复平面中的任意开集 Ω 都有一个穷举。
证明:
若 Ω 有界,我们令 表示 Ω 中距离 Ω 的边界的距离 ≥ 1/𝓁 的点的集合。若 Ω 无界,令
表示上述相同的集合(但还要求对于任意
, |z| ≤ 𝓁 ) 。
现在我们可以开始证明 Montel 定理了。 令 K 为 Ω 的一个紧子集,并选择足够小的 r > 0 ,使得对于任意 z∈K,都有 含于 Ω 中。只需选择 r 使得 3r 小于从 K 到 Ω 的边界的距离即可。令 z ,w∈K 且 | z - w | < r ,并令 γ 表示圆盘
的边界圆。则,根据 Cauchy 积分公式,我们有
。
注意到
,
因为,ζ∈γ 和 | z - w | < r 。因此,
,
其中,B 表示函数族 ℱ 在由所有 Ω 中距离 K 的距离 ≤ 2r 的点所构成的紧集合中的一致边界。因此,| f(z)- f(w)| ≤ C| z - w | ,且这个估算对于所有 z ,w∈K 且 | z - w | < r 和 f ∈ ℱ 都成立;因此,这个函数族是等度连续的,正如所要证明的。
为了证明定理的第二部分,我们按如下论证。令 为 ℱ 中的一个序列,并令 K 为 Ω 的一个紧子集。选择一个在 Ω 中是稠密的(dense)点列
。由于
是一致有界的,因此,存在
的一个子序列
,使得
收敛。
从 我们可以提取出一个子序列
使得
收敛。我们可以持续这个处理过程,提取
的一个子序列
使得
收敛。
最后,令 并考虑对角(diagonal)子序列
。根据构造,对于每一个 j ,
收敛,我们断言,等度连续意味着
在 K 上一致收敛。已经 ε > 0 ,选择和等度连续的定义中相同的 δ , 并注意到,对于某个 J ,集合 K 含于圆盘
的并集中。选一个足够大的 N 使得,如果 n, m > N,则
(对于所有 j = 1 , 2 , ... , J )。
因此,若 z∈K ,则 (对于某些 1 ≤ j ≤ J ) 。因此,
(只要 n, m > N )。
因此, 在 K 上一致收敛。
最后,我们需要一个对角化(diagonalization)参数来获得在 Ω 的每个紧子集上一致收敛的子序列。令 为 Ω 的一个穷举,并假设
是在
上一致收敛的源序列
的一个子序列。从
中提取一个在
上一致收敛的子序列
,如此,等等。则
是在每一个
一致收敛的
的子序列,且因为
穷尽 Ω ,则序列
在 Ω 的任意紧子集上一致收敛,这正是所要证明的。
在我们能够给出 Riemann 映射定理的证明之前,我们还需要一个更进一步的结论。
命题 3.5 若 Ω 是 ℂ 的一个连通开子集, 是一个 Ω 上在 Ω 的每一个紧子集上一致收敛于一个全纯函数 f 的双射全纯函数序列,则 f 是双射或常量。
证明:
我们按反证法论证,假设 f 不是双射的,因此,在 Ω 中存在不同的复数 和
使得
。用
定义一个新的序列,因此,
除了
没有其它的零点,且序列
在 Ω 的紧子集上一致收敛于
。若 g 不是恒为令,则
是 g 的一个孤立零点(因为 Ω 是连通的);因此,
,
其中,γ 是所选的使得 g 在 γ 上或在其内部除了 点不消没的一个圆心位于
的小圆。因此,
在 γ 上一致收敛于 1/g,由于
在 γ 上一致收敛,我们有
。
但这是矛盾的,因为 在 γ 内部没有零点,因此,我们有
(对于任意 n )。
3.3 Riemann映射定理的定理(Proof of the Riemann mapping theorem)
一旦我们确定了上述技术成果,则 Riemann 映射定理的其余证明就非常优雅了。它包括三个步骤,我们将其分开。
第 1 步:假设 Ω 是 ℂ 的一个简单连通直开子集。我们断言,Ω 是一个包含原点的单位圆盘的一个开子集共形等价。事实上,选择一个不属于 Ω 的复数 α ,(记得 Ω 是真子集),并注意到,z - α 在简单连通域上永不消没。因此,我们可以定义一个全纯函数
,
其具有预期的对数属性。故而,我们有 ,特别是,这证明了 f 是双射的。挑一个点 w∈Ω ,并观察到
f (z) ≠ f (w) + 2πi (对任意 z∈Ω )。
否则,我们指数化这个关系以求得 z = w ,因此,f (z) = f (w),这是矛盾的。 事实上,我们断言 f (z) 严格远离 f (w) + 2πi , 在这种意义上,存在一个圆心位于 f (w) + 2πi 不包含像 f (Ω)的点的圆盘。否则,在 Ω 中存在一个序列 使得
。我们指数化这种关系,由于这个指数函数是连续的,我们一定有
。但这意味着,
,这与以上结论相矛盾。最后,我们考虑映射
。
由于 f 是双射的,因此,F 也是双射的,故而 F :Ω ⟶ F (w) 是一个共形映射。此外,根据我们的分析,f (Ω)是有界的。因此,我们可以通过平移并缩放函数 F ,以获得从 Ω 到 𝔻 的开子集的包含原点的共形映射。
第 2 步:根据第一步,我们可以假设 Ω 是 𝔻 的一个开开子集且 0∈Ω 。考虑 Ω 上的所有映射到单位圆盘并固定了原点的双射全纯函数族 ℱ :
ℱ = { f :Ω ⟶ 𝔻 全纯,双射且 f (0) = 0 } 。
首先,我们注意到 ℱ 是非空的,因为它包含恒等。此外,根据构造,这个函数族一致有界,因为要求所有的函数映射到单位圆。
现在,我们转向求解函数 f ∈ ℱ 这个问题,此函数满足 具有最大化。首先注意到,量
在 ℱ 中随着 f 域的变化而一致有界。这一点可从
的 Cauchy 不等式应用到圆心位于原点的一个小圆盘上而推导出。接下来,我们令
,
我们选择一个序列 使得当 n ⟶∞ 时
。根据 Montel定理(定理3.3),这个序列有一个在一个紧集合上一致收敛于 Ω 上一个全纯函数 f 的子序列。由于 s ≥ 1 (因为 z ⟼ z 属于 ℱ ),因此,f 是非常量,从而是双射(根据命题 3.5 )。 此外,根据连续性,我们有| f (z)|≤1(对于任意 z∈Ω ),并根据最大模原理,我们可以发现 | f (z)| < 1 。由于我们显然有 f (0) = 0 ,因此我们推断出 f ∈ ℱ 且
。
第 3 步:在这最后一步中,我们证明 f 是一个从 Ω 到 𝔻 的共形映射。由于 f 已经是双射的,所以只需要证明 f 也是满射的即可。假如这一点不成立,则我们可以在 ℱ 中构造一个其导数在 0 点大于 s 的函数。事实上,假设存在 α∈𝔻 使得 f (z)≠ α ,并考虑交换 0 和 α 的圆盘的自同构 , 即
。
由于 Ω 是简单连通的,因此 ,此外,U 不包含原点。因此,可以在U 上定义一个平方根函数
。
接下来考虑函数
。
我们断言 F ∈ ℱ 。显然,F 是全纯的,它将 0 映射到 0 。此外,F 映射到单位圆盘,因为这对于复合中的每一个函数都成立。最后,F 是双射。这对于自同构 和
这显然成立;对于平方根 g 和函数 f 这也显然成立,因为按假设,后者是双射的。若 h 表示平方函数
,则我们一定有
。
但是,𝛟 映射 𝔻 到 𝔻 且 𝛟(0) = 0 ,并且不是双射,因为 F 是双射的而 h 不是。按照 Schwarz 引理的最后部分,我们推断出 。一旦我们注意到
,
因此,
,
这与 在 ℱ 中的极大性(maximality)相矛盾。
因此,我们用绝对值 1 的复数乘以 f 以使得 ,证明完成。
对于这个证明的一个变体,参见问题 7 。
评注:
值得指出的是,进入证明中的的简单连通性假设唯一出现的地方是使用对数和平方根的地方。因此,只需假设(除了 Ω 是真子集的假设)Ω在 对 Ω 中任意全纯函数 f 和任意闭合曲线 γ (我们有 ) 的意义上是全纯简单连通的即可。关于这一点的进一步讨论以及简单连通性的各种等价性质,请参见附录 B 。
4. 到多边形的共形映射 (Conformal mappings onto polygons)
Riemann 映射定理保证了从任何真的简单连通开(子)集到圆盘,或等价地到上半平面的共形映射的存在,但这个定理几乎没有给出关于这种映射的确切形式的信息(insight)。在第 1 节中,我们给出了具有对称性的域的各种显式公式,但要求在一般情况下给出显式公式显然是不合理的。然而,还有另一类开集,即多边形,也有很好的公式。我们在最后一节中的目标是给出 Schwarz-Christoffel 公式的证明,该公式描述了从圆盘(或上半平面)到多边形的共形映射的性质。
4.1 一些例子(Some examples)
我们从研究一些激励(motivating)例子开始。前两个对应简单(但无限(infinite)和退化的(degenerate))情况。
例子 1:
首先,我们调查从上半平面到扇形 且 0 < α < 2 的映射,由第 1 节中的
。先于以下 Schwarz-Christoffel 公式之前,我们写成
。
且 α + β = 1 ,其中的积分在上半平面中沿着任意路径进行。事实上,根据连续性和Cauchy定理,我们可以将积分路径置于上半平面的闭包中。尽管 f 的行为可直接从原定义推导出,但我们根据上面的积分表达式来研究它,因为这为后面处理的一般情况提供了见解(insight)。
首先注意到, 在 0 附近是可积的,因为 β < 1 ,因此 f (0) = 0 。观察到,当 z 为实数且为正(z = x)的时候,则
为正;此外,它在 ∞ 处并不是有限可积的。因此,随着 x 从 0 移动到 ∞ ,我们发现 f (x ) 从 0 移递增到 ∞ ,因此,f映射[0 , ∞) 到 [0 , ∞)。在另一方面,当 z = x 是负数的时候,则
,
因此,f 映射分段 (-∞,0] 到 。这种情况说明于图 3 中,其中,无限分段 A 被映射到
,而无限分段 B 被映射到
,且移动方向如图 3 所示。

-------------------------------------------图3: 共形映射 --------------------------------------------------------
例子 2:
接下来,我们考虑对于 z∈ℍ ,
,
其中,积分是沿着闭合上半平面从 0 到 z 的任意路径进行的。我们选择 的使其在上平面全纯且当 -1 < ζ < 1 时为正的分支。因此,
(当 ζ > 1)。
我们注意到,f 将实线映射到如图 4 所示的半带域的边界上。

---------------------------------------------图 4: 例子 2 中的边界映射------------------------------------------------
事实上,由于 f (±1) = ±π/2 ,且若 -1 < x < 1 则 ,我们看到 f 将分段 B 映射到
。此外,
(当 x > 1) 和
。
因此,当 x 沿着分段 C 移动的时候,其像贯穿无限分段 。类似地,分段 A 被映射到
。
注意这个例子与 1.2 节中例子 8 的联系。事实上,我们可以证明,函数 f (z )是函数 的逆,因此,f 将 ℍ 共形地映射到由
和
为边界的半带域的内部。
例子 3:
在这里我们取
。
其中,k 是一个固定的实数且 0 < k < 1 (当 ζ 是实数且 -1 < ζ < 1 时,上半平面的 被选作为正的分支)。这种积分被称为椭圆积分(elliptic integrals),因为在计算椭圆弧长的过程中会出现这些变体。我们将观察到,f 将实轴映射到如图 5(b) 所示的矩形,其中,K 和
分别确定于
,
。
我们将实轴划分成四个“分段(segments),” 分割点分别为 -1/k,-1 ,1 ,和 1/k (见图 5 (a))。这四个分段分别是 [-1/k ,-1],[-1 ,1], [1 ,1/ k],和 [1/ k ,-1/k ]。此外,由于
(若 1 < x < 1/k),
我们发现,f 将分段 [1 , 1/k] 映射到 ,其中,
定义如上。类似地,f 将分段 [-1/k , -1] 映射到
。接下来,当 x > 1/ k 时 ,我们有
,
因此,
。
然而,
,
这正是通过在积分式的左边执行变量替换 x = 1/ku 看到的结果。因此,f 将分段 [1/k , ∞) 映射到 。类似地,f 将分段 (-∞,-1/k ] 映射到
。则,合起来,f 将实轴映射到上述矩形,且无穷远点对应于矩形上边的中点。

-----------------------------------------图 5: 例子 3 中的边界映射---------------------------------------------------
迄今为止所获得的结论很自然地导致了两个问题。
第一个问题是(我们接下来要讨论的)上述例子的推广。更准确地说,我们定义了 Schwarz-Christoffel 积分,并证明它将实线(real line)映射到折线(polygonal)。
第二个问题是,我们注意到,在上面的例子中,我们很少推断出 f 在 ℍ 本身中的行为。特别是,我们没有证明 f 将 ℍ 共形映射到相应多边形的内部。在仔细研究了共形映射的边界行为后,我们证明了一个定理,该定理确保了从上半平面到由折线界定的简单连通域的共形映射在本质上是由 Schwarz-Christoffel 积分给出的。
4.2 Schwarz-Christoffel积分(The Schwarz-Christoffel integral)
带着对前面章节例子的印象,我们定义一般的 Schwarz-Christoffel 积分为
(5)
在公式中, 是 n 个按递增次序分布在实轴上的不同的点。将假设指数
满足条件: 对于每一个 k 有
和
( 注:注意
这种情况,其出现在上述示例 1 和 2 中的情况被排除在外。然而,可以对下面的命题进行修改以考虑到这些情况;但 S(z) 不再局限于上半平面)。
(5)中的积分定义如下: 是当 z = x 是实数且
时为正的分支(定义于复平面上,沿着无限的射线
)。因此,

沿着射线 的复平面狭缝(slit)是简单连通的(参见练习 9),因此,定义 S(z) 的积分在这个开集上是全纯的。因为
这个要求意味着在
附近的奇点
是可积的,函数 S 连续至实线 ( 包括点
(k = 1,...,n))。最后,这个连续条件意味着积分可以沿着复平面上避开开缝的(open slits)并集
的任意路径进行。
现在
(对于任意大的 |ζ|),
因此,假设条件 确保了积分式(5)在无穷远处收敛。这个事实再结合 Cauchy 定理就意味着
存在,而我们令
。
命题 4.1 假设 S(z)由(5)给出。
( i ) 若 ,且 𝖕 (译注:德文尖角体,Unicode: 1D595,LaTex语法:\frak{p})表示多边形,其顶点(按顺序)由
给出,则 S 将实轴映射到
。点
位于
上并且是这点在无穷远处的像。此外,在顶点
![]()
的(内部)角是
(其中,
)。
( ii ) 当 时,存在一个类似的结论,现在需除去扩展直线的像是具有
个顶点的 n + 1 条边的多边形这种情况。在顶点
处的角是
且
,其中,
。
图 6 说明了这个命题。这个证明的思想已经体现在(captured)上述例子 1 中。
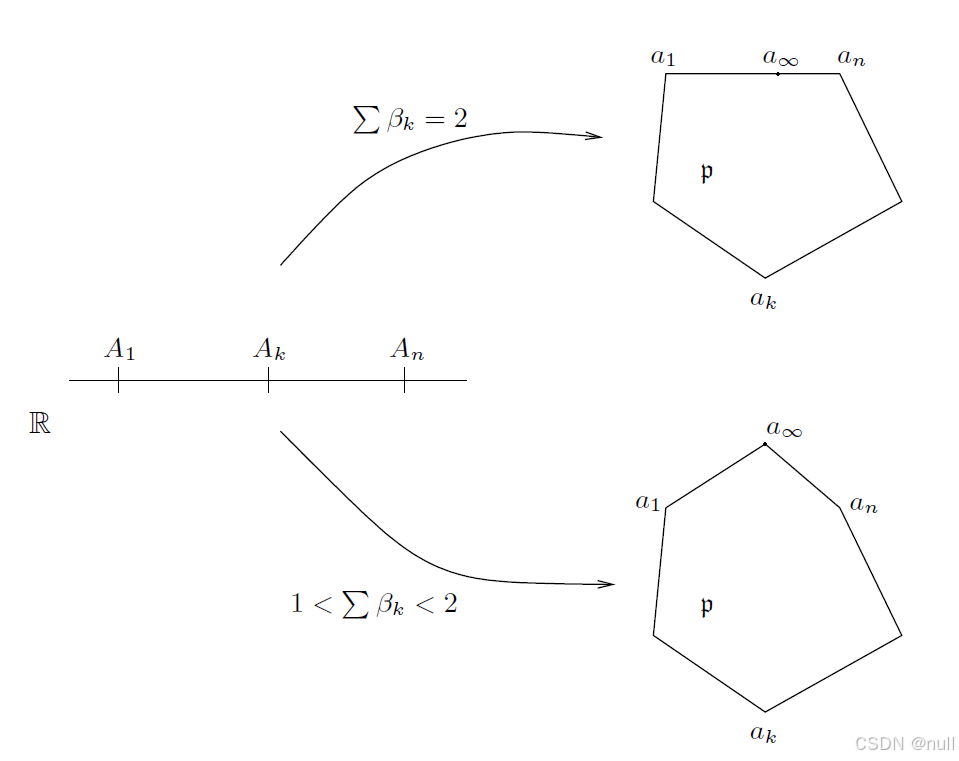
-----------------------------------------图 6:积分 S(z) 的作用(action)----------------------------------------------
证明:
我们假设 。若当
时,
,则
。
因此,
,
显然,当 x 贯穿区间 时,上式是常量。因为
,
我们看到,随着 x 从 变动到
S(x)沿着直线段(注:我们用[z,w]来表示两个复数 z 和 w 之间的闭合直线段,即,[z,w] = {(1 - y)z + tw:t∈[0,1]}。若我们限定 0 < t < 1,则用(z,w)来表示 z 和 w 之间的开直线段。类似地,可以分别限定 0 ≤ t < 1 和 0 < t ≤ 1 来获得半开直线段[z,w)和(z,w])
从
移动到
,这样,
与实轴就形成了一个角。类似地,当
时,则
是正,而若
,
的参数是
,因此,
还是为正。因此,随着 x 在
上变动 ,S(x) 在
和
之间沿着直线(平行于 x 轴)变动;类似地,随着 x 在
上变动,S(x)在
和
之间沿着直线(平行于那个轴)变动。此外,
和
的合并是分段
且点
被移除。
现在, 的角度比
增加
,意味着顶点
的角度是
。当
时的证明类似,因此留给读者去完成。
虽然这个命题很优雅,但它并没有解决从半平面到给定多边形边界域 P 的共形映射问题。这有两个原因:
I. 对于通用的 n 和泛化选择的 来说,这个多边形(在映射 S 下实轴的像)不是简单的(自身不相交即称为简单)。在一般情况下,映射 S 也不会被共形映射到上半平面。
II. 该命题也没有表明,从一个单连通区域 P(其边界是一条(闭合)折线 𝖕)开始,对于某些选择的 和简单修改,映射 S 是从 ℍ 到 P 的共形映射。然而事实确实如此,这就是我们现在要证明的结果。
4.3 边界行为(Boundary behavior)
在接下来的过程中,我们将考虑一个多边形域(polygonal region)P (即一个有界的简单连通的开集,其边界是一条(闭合)折线 𝖕 )。在这种背景下,我们总是假设这条折线是闭合的,且有时候我们称 𝖕 为一个多边形(polygon)。
为了研究从半平面 ℍ 到 P 的共形映射,我们首先考虑从圆盘 𝔻 到 P 的共形映射,及其边界行为。
定理 4.2 若 F:𝔻 ⟶ P 是一个共形映射,则 F 扩展为一个从圆盘的闭包 𝔻 到多边形域的闭包 P 的连续双射。特别是,F 产生了一个从圆盘的边界到折线 𝖕 的边界的双射。
要点在于证明,若 属于单位圆,则
存在。为了证明这一点,我们需要一个预备结论,即利用事实——若 f:U ⟶ f (U )是共形的,则
(译注:“Area”即“面积”)。
从定义 和 Jacbo 矩阵按变量替换 w = f (z)之后的行列式恰好是
这一事实(我们在第 1 章第 2.2 节的等式(4)中做出的一种观察), 即可推导出这个结论。
引理 4.3 对于每一个 0 < r < 1/2 ,令 表示圆心位于
半径为 r 的圆。假设对于任意足够小的 r ,给予我们两个位于单位圆盘中且同时也位于
上的点
和
。若我们令
,则存在一个半径(radii)趋于零的序列
, 使得
。
证明:
若不然,存在 0 < c 和 0 < R < 1/2 ,使得对于任意 0 < r ≤ R 有 c ≤ ρ(r) 。我们注意到
,
其中,积分是在 上的且由位于 𝔻 中的
和
连接的弧 α 上时行的(译注:𝔻 表示单位圆盘,
是一个圆且半径小于 1 )。若我们用
参数化这个弧,则
。
现在我们应用 Cauchy-Schwarz 不等式以后可以看到
。
对上述不等式两边进行平方并除以 r 得到
。
现在我们可以对上式两侧从 0 到 R 进行积分,由于在这个域上 c ≤ ρ(r),我们得到
。
现在,上述不等式的左侧是无限的,因为 1/r 在原点附近不可积,而不等式的右侧是有界的,因为多边形域的面积是有界的,因为这就产生了预期的矛盾,从而引理得证。
引理 4.4 令 为单位圆上的一点。则随着 z 在单位圆盘内趋近于
,F(z)趋近于一个有限值。
证明:
若不然,在单位圆盘中存在两个收敛于 的序列
和
,因此存在
和
收敛于 P 的闭包中的两个不同的点
和
由于 F 是共形的,点
和
一定位于 P 的边界 𝖕 上。因此,我们可以选择两个圆心分别位于
和
且不相交的圆盘,它们相互之间的距离 d > 0 (译注:应指两个圆盘边沿之间的距离)。对于任意大的 n,
且
。因此,在
和
中分别存在两条连续的曲线
和
(注:就连续曲线而言,我们指的是从一个闭区间[a,b]到 ℂ 的一个连续(不必是逐段平滑的)函数的像),且对于任意大的 n,有
和
,以及
和
的端点分别等于
和
。
定义 和
则
和
是 𝔻 中两条连续曲线。此外,
和
均分别包含各自对应序列
和
中的无穷多个点。我们记得,这些序列收敛于
。根据定义,圆心位于
且半径为 r 的圆
将与
和
相交(对于任意小的 r ),比如,相交于某些点
和
。这与前面的引理矛盾,因为
,因此,当 z 在单位圆盘内趋近于
时,F(z)在 𝖕 上收敛于一个极限值,证明完成。

---------------------------------------------图 7: 引理 4.4 证明的说明--------------------------------------------------
引理 4.5 共形映射 F 扩展为一个从圆盘的闭包到多边形的闭包的连续函数。
证明:
根据前面的引理,极限
存在,我们定义 为这个极限的值,还需证明 F 在单位圆盘的闭包上是连续的。任给一个 ε > 0 ,存一个 δ > 0 ,使得只要 z∈𝔻 且
,则就有
。现在,若 z 属于 𝔻 的边界且
,则我们就可以选择 w 使得 | F(z)- F(w)| < ε 且
。因此,
,
因此,引理成立。
现在,我们可以完成对定理的证明了。我们已经证明 F 扩展为一个从 到
的连续函数。前面的论证可应用于 F 的逆 G。事实上,我们用到的单位圆盘的关键几何属性在于,若
属于 𝔻 的边界,且 C 是圆心位于
任意小的圆,且 C∩𝔻 构面了一段弧。很显然,这一属性在多边形域 P 的每一个边界点上也成立。因此,G 也扩展为一个从
到
的连续函数。现在只需证明 F 和 G 的扩展互逆即可。若 z∈∂𝔻 且
是圆盘中的一个收敛于 z 的序列,则
,因此,在取极限之后再利用 F 是连续函数的事实,G(F (z)) = z (对于任意
) 。类似地,G(F (w)) = w (对于任意
),从而定理得证。
本证明中使用的理想圆可用于证明关于共形映射边界连续性的更一般定理。请参阅下面的练习 18 和问题 6。
4.4 映射公式(The mapping formula)
假设 P 是一个以多边形 𝖕 为边界的多边形域,其中,𝖕 的顶点是连续顺序的 。我们用
表示位于
处的内角,并使用
定义外角
。通过一个简单的几何论证可得到
。
我们将考虑从上半平面 ℍ 到 P 的共形映射,并使用上一节考虑的从单位圆盘 𝔻 到 P 的共形映射的结果,标准的对应关系 w = (i – z)/(i + z ), z = i(1 – w)/(1 + w )允许我们在 z∈ℍ 和 w∈𝔻 之间往返。请注意,圆的边界点 w = −1 对应于直线上的无穷远点,因此 ℍ 到 𝔻 的共形映射扩展为 ℍ 边界的连续双射,出于本讨论的目的,这包括无穷远点。
令 F 为从 ℍ 到 P 的共形映射。(其存在性由 Riemann 映射定理和前面的讨论保证。) 我们首先假设 𝖕 上没有顶点对应于无穷远点。因此,存在实数 使得
(对于任意 k )。由于 F 是连续且双射的,并且顶点是按连续编号标号的,我们可以推断出,有序实数序列
是按序增或按序降的。我们对顶角
和点
重新标号后,我们可以假设
。这些点将实线划分成 (n - 1)个分段
,而这个段由两个半段的联合
构成。这些分段被按双射映射到多边形的相应边上,多边形的相应边即指这些分段
和
(见图 8 )。

---------------------------------------------------------图 8: 映射 F ---------------------------------------------------
定理 4.6 存在复数 和
,使得从 ℍ 到 P 的共形映射 F 由
给出,其中,S 是在 4.2 节中引入的 Schwarz-Christoffel 积分。
证明:
我们首先考虑位于两个相邻分段 和
( 1 < k < n ) 上方的上半平面中的 z 。我们注意到,F 将这两个段映射到以
角相交于
的两个分段。
通过选择对数的一个分支,则反过来,对于上半平面中以直线 和
为边界的半带域中的任意 z ,我们可以定义
。
由于 F 连续至 ℍ 的边界,映射 实际上在实线上连续至分段
。根据构造,
将映射分段
到复平面上的一条(直)线段
,且
被映射到 0 。因此,我们可以应用 Schwarz 反射原理以看到,
在双向无限带域
中可解析地延拓为一个全纯函数(见图 9 )。我们断言,
在那个带域中永不消没。首先,若 z 属于开的上半带域,则
,
而因为 F 是共形的,我们有 ,因此有
(命题 1.1)。根据反射,上式对于位于下半带域中的 z 也成立,而余下的问题就只剩下调查分段
上的点。若
,,则我们注意到,一个圆心位于 x 且包含于 ℍ 中的小半圆盘在映射
下的像位于直线段
的一侧。由于
是至
的双射(因为 F 也是),则 Schwartz 反射原理的对称性确保了
在整个圆心位于 x 的圆盘中是双射的,对于带域
中的任意 z ,由
可知
。

-------------------------------------------------图 9: Schwartz 反射 -------------------------------------------------
现在,因为 和
, 事实
意味着
,
其中, 在带域
内是全纯函数。对于 k = 1 和 k = n,类似的结论与成立。即
,
其中, 在带域
中是全纯的。最后,再次应用反射原理证明了 F 在圆盘 | z |≤ R 的外部是可延拓的(对于任意大的 R,比如
)。事实上,我们可以跨越整个分段并集
延拓 F ,因为这些分段在 F 下的像是一条直线段,并且适用于 Schwartz 反射原理。 F 将上半平面映射到有界区域这一事实表明,F 在大型圆盘外的解析延续也是有界的,因此在无穷远处是全纯的。因此,
在无穷远处是全纯的,我们断言当 | z| ⟶ ∞ 时,这个比值趋近于 0 。事实上,我们可以在 z = ∞ 处将 F 展开为
。
对此微分之后,可以证明 像 1/z 那样, 随着 |z| 变得无穷大而递降,从而证明了我们的断言。
然后,由于各个带域相互重叠并覆盖了整个复平面,结合在一起,就有
在整个复平面上是全纯的,并在无穷远处消没;因此,根据 Liouville 定理,上式等于 0 。因此,
。
据此,我们断言 。事实上,用 Q(z) 表示这个乘积,我们有
。
因此,
,
这样我们就证明了我们的声称(contention)。最后进行积分得到了这个定理。
现在我们可以撤回一开始的假设,即 F 没有将无穷远点映射到 P 的顶点,并且得到针对这种情况的公式。
定理 4.7 若 F 是一个从上半平面到多边形域 P 的共形映射,且将点 映射到 𝖕 的顶点,则存在常量
和
使得
。
换句话,这个公式是通过删除掉 Schwarz-Christoffel 积分(5)中的最后一项而获得的。
证明:
经过一段预先的平移之后,我们可以假设 ( j = 1, ... , n – 1 )。我们在实线上选对一个点
,考虑定义为
的分数线性映射。则 Φ 是上半平面的一个自同构。令 ,并注意到
。则
(对于任意 k = 1 ,...,n)。
现在我们可以应用刚刚证明的 Schwarz-Christoffel 公式来求得
。
变量替换 ζ = Φ(w) 满足 ,由于我们可以写成
,我们得到
。
最后,注意到, ,并在上面的等式中设
,便推导出
,
这正是所要证明的。
4.5 回到椭圆积分(Return to elliptic integrals)
我们再次考察椭圆积分
,
其出现在4.1节的例子 3 中。我们已经看到,它将实轴映射到具有顶点 –K ,K , 和
的矩形 R 。现在我们将看到,这个映射是 ℍ 到 R 的内部的共形映射。
根据定理 4.6 ,存在一个到矩形的共形映射 F ,其将四个实轴上的点映射到 R 的顶点。通过在此映射前面加上 ℍ 的适当自同构,我们可以假设 F 分别将 -1,0,1 映射到 –K ,0 ,K 。事实上,通过使用预备的自同构,我们可以假设 –K ,0 ,K 是点 ,0 ,
的像;然后,我们可以进一步取
和
。见练习 15 。
接下来,令 𝓁 (0 < 𝓁 < 1 )为所选的使得 1/𝓁 是实线上被 F 映射到(矩形的)顶点 的一点,这是一个在顺序上紧邻–K 和 K 之后的顶点。我们断言 F (-1/𝓁 )是顶点
。事实上,若
,则根据矩形 R 的对称性,
也是一个 ℍ 到 R 的共形映射;些外,
且
。因此,
是 ℍ 的一个固定了点 -1,0,和 1 的自同构。因此,
是恒等(映射)(见练习 15 ),且
,据此可推导出
。
因此, 根据定理 4.6 有
。
令 z = 0 给出 ,而令 z = 1 ,z = 1/ 𝓁 ,得到
和
,
其中,
,
。
现在,K(k)显然是严格地随着 k 在(0,1)内的变化而递增的。此外,通过一个变量替换(练习 24)建立了恒等式
(其中,
且
) ,
这就证明了 是严格递降的。因此,
是严格递增的。由于
,则我们一定有 k = 𝓁 ,最后得到
。这就证明了 I (z ) = F (z ) , 因此 I (z )是共形的,这正是所要证明的。
最后的一个观察很重要。对椭圆积分的基本理解是通过转到其反函数来实现的。因此,我们考虑 z ⟼ sn(z) ( z ⟼ I (z) 的逆映射)(注:形式略有不同的记法 sn(z) 源于 Jacobi ,并因为与 sinz
![]()
类似而被采用)。它将闭合的矩形转换到闭合的上半平面。现在考虑通过沿着矩形的下边沿连续反射而获得的矩形序列 (如图 10 所示)。
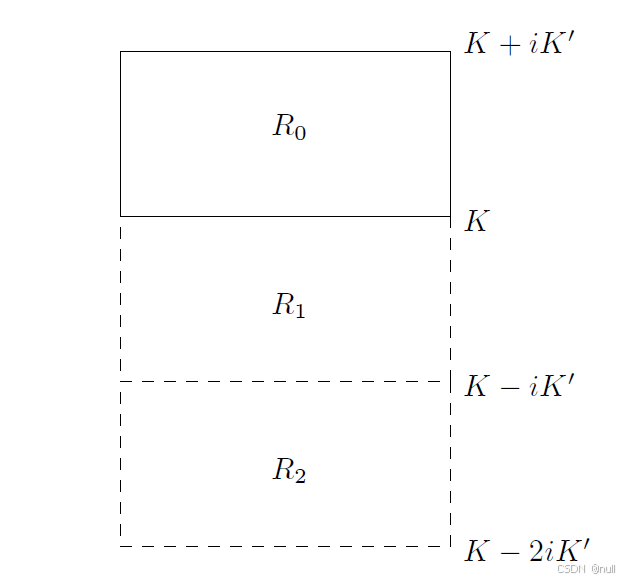
------------------------------------------------图 10: 的反射-------------------------------------------------
对于定义于 的 sn(z),我们可以使用反射原理将扩展到
,方法是设
(只要
)( 注意,
)。接下来,我们可以将 sn(z)扩展到
, 方法是设
( 若
),并注意到若
,则
。将这些反射组合起来并继续按这种方式扩展,我们可以在整个带域 –K < Re(z) < K 上扩展 sn(z) ,以使得
。
类似地,通过在一系列水平矩形中反射,并将它们与之前的反射相结合,我们看到 sn(z) 可以延拓至复平面且也满足 sn(z) = sn( z + 4 K )。因此,sn(z)是双周期的(具有周期 4 K 和 )。进一步检验表明,唯一的奇点 sn(z) 是极点。这种类型的函数(被称为“椭圆函数(elliptic functions)”)是下一章的主题。
内容来源:
<< Complex Analysis >> ,作者:E.M. Stein & R. Shakarchi
术语参考资料:
<<英汉数学词汇>>,张鸿林,葛显良 编订,清华大学比版社,2018年
<<新英汉数学词汇>> ,科学出版社名词室,科学出版社, 2002年
<<物理学名词>>,第三版,科学出版社会,2019年
<<英汉综合物理学词汇>> 科学出版社,1999年