文章目录
- 数据处理与拟合模型
- 1. 数据与大数据
- 1.1 什么是数?什么是数据?
- 1.2 数据与大数据
- 1.3 数据科学的研究对象
- 2. 数据的预处理
- 2.1 为什么需要数据预处理
- 2.2 使用pandas处理数据的基础
- 2.3 pandas常用方法总结
- 2.4 数据的规约
- 1) 维度规约
- 2) 数值规约
- 3) 数据压缩
- 4) 数据规范化
- 4.1) 最小-最大规范化
- 公式
- 例子
- 4.2) Z-Score规范化
- 公式
- 例子
- 示例代码
- 5) 数据聚合
- 6) 数据变换
- pandas处理数据示例
- 3. 常见的统计分析模型
- 3.1 回归分析与分类分析
- 回归分析
- 分类分析
- 3.2 假设检验
- 3.3 随机过程与随机模拟
- 随机过程
- 随机模拟
- `simpy` 实现随机过程仿真
- `simpy.Environment` 方法详细介绍
- 案例1: 随机模拟车流量
- 代码详解
- 案例2: 随机模拟商店营业额
- 案例3: 随机模拟病毒状态转移
- 示例代码
- 输出结果
- 结果解释
- 代码解释
- 1)函数定义
- 2)初始化状态转移矩阵
- 3)进行N次转移
- 4)计算最终状态分布
- 4. 数据可视化
- 4.1 Python三大数据可视化工具库的简介
- (1)Matplotlib:
- (2)Seaborn:
- (3)Plotnine:
- 4.2 基本图表Quick Start
- 5. 插值模型
- 5.1 线性插值法
- 公式
- 代码示例
- 5.2 三次样条插值
- 公式
- 代码示例
- 5.3 拉格朗日插值
- 公式
- 代码示例
- 分析插值效果
- 6. 知识拓展
- 6.1 指数分布与泊松分布的关系和区别
- 指数分布与泊松分布的关系
- `np.random.exponential`
- `np.random.poisson`
- 指数分布与泊松分布的区别
- 画图
- 6.2 马尔可夫链 (Markov Chain)
- 定义
- 公式
- 示例
- 代码示例
- 7. 学习心得
数据处理与拟合模型
1. 数据与大数据
1.1 什么是数?什么是数据?
数 是数学的基本概念,表示量的大小、顺序或类别。数可以是整数、分数、小数等。数的概念广泛应用于各种科学和工程领域。
数据 是数和信息的集合,用来描述和表示事物的特征、状态或变化。数据可以是定量的(如数值、测量值)或定性的(如文本、图像)。数据的特点包括:
- 多样性:数据可以以不同的形式存在,如结构化数据(表格、数据库)、非结构化数据(文本、图片、视频)和半结构化数据(XML、JSON)。
- 时效性:数据可以是实时生成的,也可以是历史积累的。
- 真实性:数据需要尽可能准确和可靠,以确保分析和决策的正确性。
1.2 数据与大数据
大数据 是指无法用传统的数据处理工具和方法在合理时间内获取、存储、管理和分析的数据集合。大数据的特点通常被称为“5V”:Volume(体量)、Velocity(速度)、Variety(多样性)、Veracity(真实性)和 Value(价值)。
- 体量(Volume):大数据的规模非常庞大,数据量级通常以TB、PB甚至更高计量。
- 速度(Velocity):大数据的生成和处理速度非常快,尤其是在物联网、社交媒体等领域,数据是实时产生和需要实时处理的。
- 多样性(Variety):大数据来自各种来源,以多种格式存在,包括结构化数据、半结构化数据和非结构化数据。
- 真实性(Veracity):大数据包含噪音和异常值,需要通过数据清洗和处理来提高数据的准确性和可靠性。
- 价值(Value):大数据的分析可以为企业和组织提供深刻的洞察和竞争优势。
大数据的应用领域非常广泛,包括:
- 商业智能:通过分析客户行为、市场趋势等数据,帮助企业做出更明智的决策。
- 医疗健康:通过分析患者数据、疾病模式等,提高医疗服务质量和效率。
- 智能交通:通过分析交通流量数据,优化交通管理和路线规划。
- 金融服务:通过分析交易数据、风险数据等,提高风险管理和决策能力。
1.3 数据科学的研究对象
数据科学 是一个跨学科领域,涉及统计学、计算机科学和领域知识,旨在通过数据分析和处理,提取有价值的信息和知识。数据科学的研究对象主要包括:
- 数据收集:从各种来源获取数据,如数据库、传感器、社交媒体、公共数据集等。
- 数据清洗和预处理:处理缺失值、噪音和异常值,确保数据的质量和一致性。
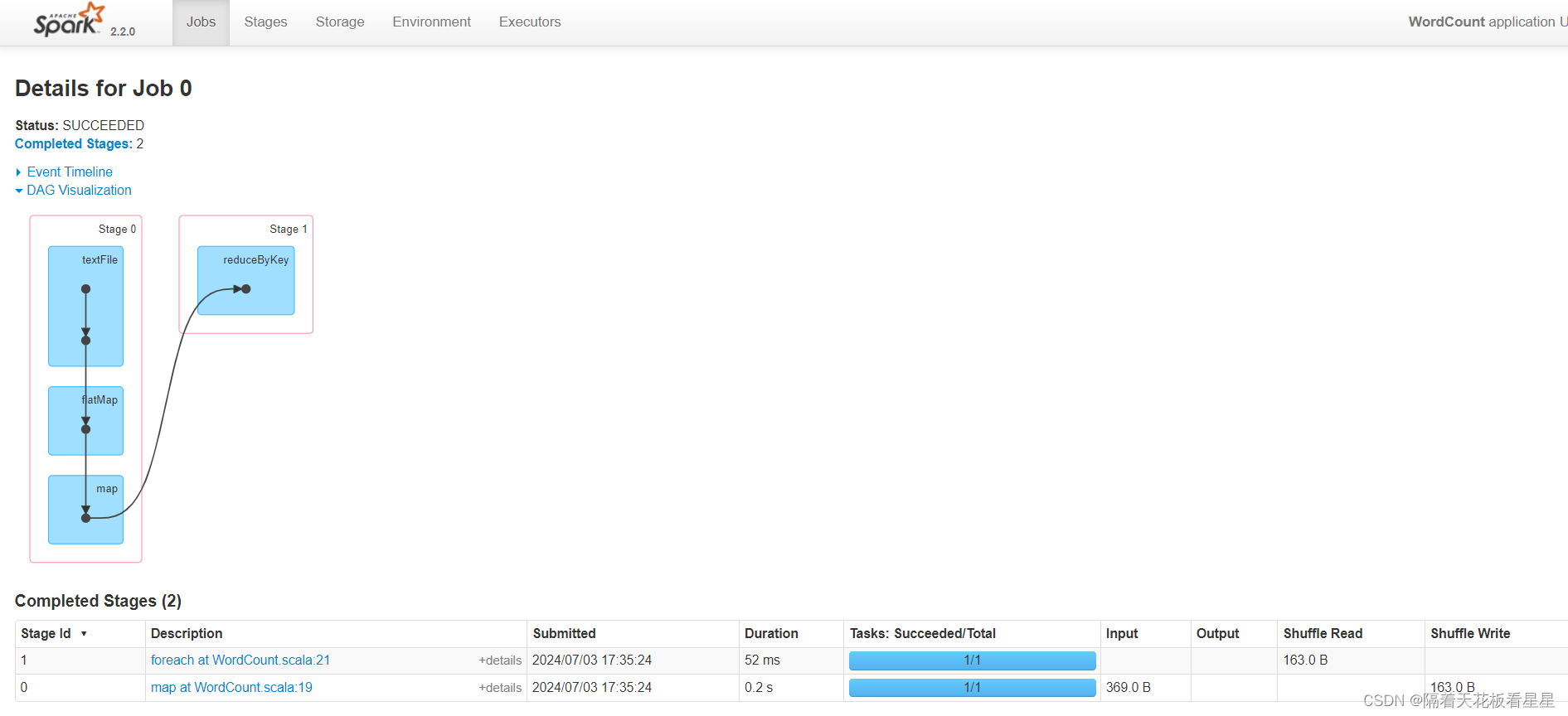
- 数据存储和管理:使用适当的技术和工具存储和管理大规模数据,如数据库管理系统、大数据平台(如Hadoop、Spark)等。
- 数据分析和挖掘:应用统计学方法、机器学习算法等,从数据中提取有用的信息和模式。
- 数据可视化:使用图表、图形等方式展示数据分析结果,帮助理解和决策。
- 预测分析和建模:建立数学模型预测未来趋势和行为,支持决策和优化。
- 机器学习和人工智能:开发和应用算法,使计算机能够从数据中学习和改进,实现自动化和智能化。
数据科学在各个行业的应用:
- 商业:客户分析、市场预测、个性化推荐。
- 医疗:疾病预测、药物研发、个性化治疗。
- 金融:风险评估、欺诈检测、投资策略。
- 政府:公共安全、政策制定、城市规划。
- 交通:交通流量预测、路线优化、自动驾驶。
数据科学的目标是通过系统化的方法,从海量数据中提取有意义的信息和知识,支持决策和创新,推动各行各业的发展和进步。
2. 数据的预处理
2.1 为什么需要数据预处理
数据预处理是数据分析和机器学习中一个重要的步骤。其主要目的是为了清理数据,确保数据的一致性、完整性和可用性,从而提高数据分析的准确性和效率。数据预处理的具体作用包括:
- 处理缺失值:缺失值可能会影响模型的性能,需要适当地填充或删除。
- 处理异常值:异常值可能会对分析结果产生误导,需要识别和处理。
- 数据格式转换:将数据转换为模型能够理解的格式,如数值化、标准化等。
- 特征工程:从原始数据中提取有用的特征,以提高模型的预测能力。
- 数据清洗:去除重复数据、处理错误数据等,以提高数据质量。
2.2 使用pandas处理数据的基础
在使用pandas进行数据预处理时,常用的函数和方法包括读取数据、选择和过滤数据、处理缺失值、数据转换和分组等。以下是一个具体示例及其分析:
import pandas as pd
import numpy as np
# 示例数据
data = {
'animal': ['cat', 'cat', 'snake', 'dog', 'dog', 'cat', 'snake', 'cat', 'dog', 'dog'],
'age': [2.5, 3, 0.5, np.nan, 5, 2, 4.5, np.nan, 7, 3],
'visits': [1, 3, 2, 3, 2, 3, 1, 1, 2, 1],
'priority': ['yes', 'yes', 'no', 'yes', 'no', 'no', 'no', 'yes', 'no', 'no']
}
labels = ['a', 'b', 'c', 'd', 'e', 'f', 'g', 'h', 'i', 'j']
df = pd.DataFrame(data, index=labels)
# 显示数据描述
print(df.describe())
# 显示前五行
print(df.head(5))
# 选择特定列
print(df[['animal', 'age']])
# 选中visits等于3的行
print(df.loc[df['visits'] == 3, :])
# 选择age为缺失值的行
print(df.loc[df['age'].isna(), :])
# 选择animal是cat且age小于3的行
print(df.loc[(df['animal'] == 'cat') & (df['age'] < 3), :])
# 选择age在2到4之间的数据(包含边界值)
print(df.loc[(df['age'] >= 2) & (df['age'] <= 4), :])
# 将'f'行的age改为1.5
df.loc['f', 'age'] = 1.5
print(df.loc['f', :])
# 对visits列的数据求和
print(df['visits'].sum())
# 计算每种animal age的平均值
print(df.groupby(['animal'])['age'].mean())
# 进阶处理
df2 = pd.DataFrame({
'From_To': ['LoNDon_paris', 'MAdrid_miLAN', 'londON_StockhOlm', 'Budapest_PaRis', 'Brussels_londOn'],
'FlightNumber': [10045, np.nan, 10065, np.nan, 10085],
'RecentDelays': [[23, 47], [], [24, 43, 87], [13], [67, 32]],
'Airline': ['KLM(!)', '<Air France> (12)', '(British Airways. )', '12. Air France', '"Swiss Air"']
})
# 填充FlightNumber中的缺失值
df2['FlightNumber'] = df2['FlightNumber'].interpolate().astype(int)
print(df2['FlightNumber'])
# 拆分From_To列
temp = df2['From_To'].str.split('_', expand=True)
temp.columns = ['From', 'To']
temp['From'] = temp['From'].str.capitalize()
temp['To'] = temp['To'].str.capitalize()
df2.drop('From_To', axis=1, inplace=True)
df2[['From', 'To']] = temp
# 清除Airline列中的特殊字符
df2['Airline'] = df2['Airline'].str.extract(r'([a-zA-Z\s]+)', expand=False).str.strip()
# 处理RecentDelays列
delays = df2['RecentDelays'].apply(pd.Series)
delays.columns = ['delay_%s' % i for i in range(1, len(delays.columns) + 1)]
df2 = df2.drop('RecentDelays', axis=1).join(delays)
# 填充delay列的NaN值
for i in range(1, len(delays.columns) + 1):
df2[f'delay_{i}'] = df2[f'delay_{i}'].fillna(np.mean(df2[f'delay_{i}']))
# 增加一行与FlightNumber=10085的行一致的行
df2 = df2._append(df2.loc[df2['FlightNumber'] == 10085, :])
# 去重
df2 = df2.drop_duplicates()
print(df2)
2.3 pandas常用方法总结
-
数据选择与过滤
df.describe(): 显示数据的基本统计描述。df.head(n): 显示数据前n行。df[['col1', 'col2']]: 选择特定的列。df.loc[condition, :]: 根据条件选择行。
-
处理缺失值
df.isna(): 检查缺失值。df.fillna(value): 用指定值填充缺失值。df.dropna(): 删除包含缺失值的行。
-
数据转换
df.astype(type): 转换数据类型。df['col'].str.extract(pattern): 提取符合正则表达式的子字符串。
-
数据分组
df.groupby(['col'])['col2'].mean(): 按照col分组,计算col2的均值。
-
高级数据操作
df['col'].apply(function): 对列应用函数。df.str.split(delimiter, expand=True): 按指定分隔符拆分字符串。df.interpolate(): 插值法填充缺失值。df._append(row): 向数据框添加新行。df.drop_duplicates(): 删除重复行。
这些函数和方法是pandas库中常用的工具,可以高效地进行数据预处理和分析。通过对数据的清洗、转换和分组等操作,可以提高数据的质量,为后续的数据分析和建模打下坚实的基础。
2.4 数据的规约
数据规约 是指在数据处理中,通过对数据进行简化和压缩,以减少数据的存储需求、提高数据处理效率的过程。规约技术的应用不仅可以降低数据存储和传输的成本,还能使数据分析更加高效、准确。数据规约主要包括以下几种方法:
1) 维度规约
维度规约 是通过减少数据集的维度来简化数据的一种方法。高维数据可能导致计算复杂性增加和过拟合问题,因此降低维度可以提高模型的性能。常见的维度规约方法包括:
- 主成分分析(PCA):通过线性变换,将高维数据投影到较低维度的子空间,保留数据的主要信息。
- 线性判别分析(LDA):基于类标签的信息,找到可以最大化类间差异和最小化类内差异的投影方向。
- 特征选择:选择对目标变量有较强解释力的特征,忽略无关或冗余的特征。
2) 数值规约
数值规约 是通过减少数值数据的数量或范围来简化数据的方法。常见的数值规约技术包括:
- 离散化:将连续数值数据转换为离散类别数据,如将年龄数据划分为年龄段。
- 聚类:通过聚类算法将相似的数据点聚合成一个簇,使用簇中心来表示这些数据点。
- 数据抽样:从原始数据集中抽取一个代表性子集,用于模型训练和测试。
3) 数据压缩
数据压缩 是通过编码技术将数据进行压缩,以减少数据的存储空间。数据压缩分为无损压缩和有损压缩两种:
- 无损压缩:在压缩和解压缩过程中不会丢失任何信息,常见的无损压缩算法包括Huffman编码、Lempel-Ziv-Welch (LZW) 算法等。
- 有损压缩:在压缩过程中会丢失部分信息,但能大幅度减少数据量,常用于图像、音频和视频的压缩,如JPEG、MP3、MP4等。
4) 数据规范化
数据规范化 是通过将数据缩放到同一尺度来简化数据处理的方法,常见的规范化技术包括:
- 最小-最大规范化:将数据缩放到一个固定范围(通常是0到1)。
- Z-Score规范化:将数据转换为均值为0、标准差为1的标准正态分布。
4.1) 最小-最大规范化
最小-最大规范化(Min-Max Normalization)将数据缩放到一个固定范围,通常是0到1。这个方法可以使不同特征的数据具有相同的尺度,有助于提升某些机器学习算法的性能。
公式
x ′ = x − min ( x ) max ( x ) − min ( x ) x' = \frac{x - \min(x)}{\max(x) - \min(x)} x′=max(x)−min(x)x−min(x)
其中:
- x x x 是原始数据值。
- x ′ x' x′ 是规范化后的数据值。
- min ( x ) \min(x) min(x) 是数据集中最小的值。
- max ( x ) \max(x) max(x) 是数据集中最大的值。
例子
假设有一组数据: x = [ 1 , 2 , 3 , 4 , 5 ] x = [1, 2, 3, 4, 5] x=[1,2,3,4,5]
根据公式,首先确定最小值和最大值:
- min ( x ) = 1 \min(x) = 1 min(x)=1
- max ( x ) = 5 \max(x) = 5 max(x)=5
将每个数据值规范化:
- x 1 ′ = 1 − 1 5 − 1 = 0 x'_1 = \frac{1 - 1}{5 - 1} = 0 x1′=5−11−1=0
- x 2 ′ = 2 − 1 5 − 1 = 0.25 x'_2 = \frac{2 - 1}{5 - 1} = 0.25 x2′=5−12−1=0.25
- x 3 ′ = 3 − 1 5 − 1 = 0.5 x'_3 = \frac{3 - 1}{5 - 1} = 0.5 x3′=5−13−1=0.5
- x 4 ′ = 4 − 1 5 − 1 = 0.75 x'_4 = \frac{4 - 1}{5 - 1} = 0.75 x4′=5−14−1=0.75
- x 5 ′ = 5 − 1 5 − 1 = 1 x'_5 = \frac{5 - 1}{5 - 1} = 1 x5′=5−15−1=1
规范化后的数据为: x ′ = [ 0 , 0.25 , 0.5 , 0.75 , 1 ] x' = [0, 0.25, 0.5, 0.75, 1] x′=[0,0.25,0.5,0.75,1]
4.2) Z-Score规范化
Z-Score规范化(Z-Score Normalization),也称为标准化(Standardization),将数据转换为均值为0、标准差为1的标准正态分布。这种方法特别适用于数据存在不同的量纲或单位时。
公式
x ′ = x − μ σ x' = \frac{x - \mu}{\sigma} x′=σx−μ
其中:
- x x x 是原始数据值。
- x ′ x' x′ 是规范化后的数据值。
- μ \mu μ 是数据的均值。
- σ \sigma σ 是数据的标准差。
例子
假设有一组数据: x = [ 1 , 2 , 3 , 4 , 5 ] x = [1, 2, 3, 4, 5] x=[1,2,3,4,5]
计算均值和标准差:
- 均值 μ = 1 + 2 + 3 + 4 + 5 5 = 3 \mu = \frac{1 + 2 + 3 + 4 + 5}{5} = 3 μ=51+2+3+4+5=3
- 标准差 σ = ( 1 − 3 ) 2 + ( 2 − 3 ) 2 + ( 3 − 3 ) 2 + ( 4 − 3 ) 2 + ( 5 − 3 ) 2 5 = 2 ≈ 1.414 \sigma = \sqrt{\frac{(1-3)^2 + (2-3)^2 + (3-3)^2 + (4-3)^2 + (5-3)^2}{5}} = \sqrt{2} \approx 1.414 σ=5(1−3)2+(2−3)2+(3−3)2+(4−3)2+(5−3)2=2≈1.414
将每个数据值标准化:
- x 1 ′ = 1 − 3 1.414 ≈ − 1.414 x'_1 = \frac{1 - 3}{1.414} \approx -1.414 x1′=1.4141−3≈−1.414
- x 2 ′ = 2 − 3 1.414 ≈ − 0.707 x'_2 = \frac{2 - 3}{1.414} \approx -0.707 x2′=1.4142−3≈−0.707
- x 3 ′ = 3 − 3 1.414 = 0 x'_3 = \frac{3 - 3}{1.414} = 0 x3′=1.4143−3=0
- x 4 ′ = 4 − 3 1.414 ≈ 0.707 x'_4 = \frac{4 - 3}{1.414} \approx 0.707 x4′=1.4144−3≈0.707
- x 5 ′ = 5 − 3 1.414 ≈ 1.414 x'_5 = \frac{5 - 3}{1.414} \approx 1.414 x5′=1.4145−3≈1.414
标准化后的数据为: x ′ = [ − 1.414 , − 0.707 , 0 , 0.707 , 1.414 ] x' = [-1.414, -0.707, 0, 0.707, 1.414] x′=[−1.414,−0.707,0,0.707,1.414]
示例代码
以下是使用pandas进行最小-最大规范化和Z-Score规范化的示例代码:
import pandas as pd
import numpy as np
# 创建示例数据
data = {'value': [1, 2, 3, 4, 5]}
df = pd.DataFrame(data)
# 最小-最大规范化
df['min_max_normalized'] = (df['value'] - df['value'].min()) / (df['value'].max() - df['value'].min())
# Z-Score规范化
df['z_score_normalized'] = (df['value'] - df['value'].mean()) / df['value'].std()
print("原始数据:")
print(df['value'])
print("\n最小-最大规范化后的数据:")
print(df['min_max_normalized'])
print("\nZ-Score规范化后的数据:")
print(df['z_score_normalized'])
运行结果:
原始数据:
0 1
1 2
2 3
3 4
4 5
Name: value, dtype: int64
最小-最大规范化后的数据:
0 0.00
1 0.25
2 0.50
3 0.75
4 1.00
Name: min_max_normalized, dtype: float64
Z-Score规范化后的数据:
0 -1.414214
1 -0.707107
2 0.000000
3 0.707107
4 1.414214
Name: z_score_normalized, dtype: float64
通过上述方法和例子,可以更好地理解和应用数据规范化技术,从而提高数据处理和分析的效果。
5) 数据聚合
数据聚合 是通过对数据进行汇总和合并来简化数据的方法。常见的数据聚合技术包括:
- 分组聚合:根据某些特征对数据进行分组,并计算每个组的统计量,如均值、总和、计数等。
- 时间序列聚合:对时间序列数据进行汇总,如按天、周、月等时间间隔进行数据聚合。
6) 数据变换
数据变换 是通过应用数学函数对数据进行转换,以简化数据结构或突出数据特征。常见的数据变换技术包括:
- 对数变换:将数据转换为对数值,以减少数据的变化范围。
- 幂变换:将数据转换为幂值,以调整数据的分布形态。
- Box-Cox变换:一种广泛使用的幂变换,用于将非正态分布数据转换为接近正态分布。
pandas处理数据示例
通过以下示例代码,可展示如何使用pandas进行数据规约操作:
import pandas as pd
import numpy as np
from sklearn.decomposition import PCA
# 示例数据
data = {
'animal': ['cat', 'cat', 'snake', 'dog', 'dog', 'cat', 'snake', 'cat', 'dog', 'dog'],
'age': [2.5, 3, 0.5, np.nan, 5, 2, 4.5, np.nan, 7, 3],
'visits': [1, 3, 2, 3, 2, 3, 1, 1, 2, 1],
'priority': ['yes', 'yes', 'no', 'yes', 'no', 'no', 'no', 'yes', 'no', 'no']
}
labels = ['a', 'b', 'c', 'd', 'e', 'f', 'g', 'h', 'i', 'j']
df = pd.DataFrame(data, index=labels)
# 填充缺失值
df['age'] = df['age'].fillna(df['age'].mean())
# 离散化示例
df['age_group'] = pd.cut(df['age'], bins=[0, 2, 4, 6, 8], labels=['0-2', '2-4', '4-6', '6-8'])
# 特征选择示例
df_selected = df[['animal', 'age', 'visits']]
# PCA降维示例
pca = PCA(n_components=2)
df_pca = pd.DataFrame(pca.fit_transform(df[['age', 'visits']]), columns=['PC1', 'PC2'])
# 数据规范化示例
df['visits_normalized'] = (df['visits'] - df['visits'].min()) / (df['visits'].max() - df['visits'].min())
# 数据聚合示例
df_grouped = df.groupby('animal').agg({'age': 'mean', 'visits': 'sum'})
print("原始数据:")
print(df)
print("\n离散化后的数据:")
print(df[['age', 'age_group']])
print("\n特征选择后的数据:")
print(df_selected)
print("\nPCA降维后的数据:")
print(df_pca)
print("\n规范化后的数据:")
print(df[['visits', 'visits_normalized']])
print("\n聚合后的数据:")
print(df_grouped)
通过这些数据规约方法,可以有效地简化数据,提高数据处理和分析的效率和准确性。这些方法在实际应用中可以灵活组合和调整,以满足不同的需求和目标。
3. 常见的统计分析模型
统计分析模型是数据分析中常用的工具,通过这些模型可以从数据中提取有价值的信息、预测未来的趋势、理解变量之间的关系等。以下是一些常见的统计分析模型。
3.1 回归分析与分类分析
回归分析
回归分析是一种用于研究变量之间关系的统计方法,特别是用于研究一个或多个自变量(独立变量)与因变量(依赖变量)之间的关系。回归分析可以分为简单线性回归和多元线性回归。
1. 简单线性回归
简单线性回归分析一种自变量对因变量的影响,公式如下:
y
=
β
0
+
β
1
x
+
ϵ
y = \beta_0 + \beta_1 x + \epsilon
y=β0+β1x+ϵ
其中:
- y y y 是因变量
- x x x 是自变量
- β 0 \beta_0 β0 是截距
- β 1 \beta_1 β1 是自变量的回归系数
- ϵ \epsilon ϵ 是误差项
2. 多元线性回归
多元线性回归分析多个自变量对因变量的影响,公式如下:
y
=
β
0
+
β
1
x
1
+
β
2
x
2
+
…
+
β
p
x
p
+
ϵ
y = \beta_0 + \beta_1 x_1 + \beta_2 x_2 + \ldots + \beta_p x_p + \epsilon
y=β0+β1x1+β2x2+…+βpxp+ϵ
其中:
- x 1 , x 2 , … , x p x_1, x_2, \ldots, x_p x1,x2,…,xp 是多个自变量
- β 1 , β 2 , … , β p \beta_1, \beta_2, \ldots, \beta_p β1,β2,…,βp 是对应的回归系数
分类分析
分类分析是一种用于对数据进行分类的统计方法。常见的分类分析方法有逻辑回归(Logistic Regression)、支持向量机(SVM)、决策树(Decision Tree)等。
1. 逻辑回归
逻辑回归用于分类问题,通过将线性回归的结果映射到(0, 1)区间来进行二分类。公式如下:
P
(
y
=
1
∣
x
)
=
1
1
+
e
−
(
β
0
+
β
1
x
1
+
β
2
x
2
+
…
+
β
p
x
p
)
P(y=1|x) = \frac{1}{1 + e^{-(\beta_0 + \beta_1 x_1 + \beta_2 x_2 + \ldots + \beta_p x_p)}}
P(y=1∣x)=1+e−(β0+β1x1+β2x2+…+βpxp)1
其中:
- P ( y = 1 ∣ x ) P(y=1|x) P(y=1∣x) 表示在给定 x x x 的情况下 y y y 为 1 的概率
3.2 假设检验
假设检验是统计学中用于检验数据中假设是否成立的方法。假设检验包括提出假设、选择显著性水平、计算检验统计量和作出决策等步骤。常见的假设检验包括t检验、卡方检验和方差分析。
1. t检验
t检验用于比较两个组的均值是否存在显著差异。公式如下:
t
=
X
ˉ
1
−
X
ˉ
2
s
1
2
n
1
+
s
2
2
n
2
t = \frac{\bar{X}_1 - \bar{X}_2}{\sqrt{\frac{s_1^2}{n_1} + \frac{s_2^2}{n_2}}}
t=n1s12+n2s22Xˉ1−Xˉ2
其中:
- X ˉ 1 , X ˉ 2 \bar{X}_1, \bar{X}_2 Xˉ1,Xˉ2 是两个样本组的均值
- s 1 2 , s 2 2 s_1^2, s_2^2 s12,s22 是两个样本组的方差
- n 1 , n 2 n_1, n_2 n1,n2 是两个样本组的样本量
2. 卡方检验
卡方检验用于检验两个分类变量是否独立。公式如下:
χ
2
=
∑
(
O
i
−
E
i
)
2
E
i
\chi^2 = \sum \frac{(O_i - E_i)^2}{E_i}
χ2=∑Ei(Oi−Ei)2
其中:
- O i O_i Oi 是观测频数
- E i E_i Ei 是期望频数
3. 方差分析(ANOVA)
方差分析用于比较三个或更多组的均值是否存在显著差异。公式如下:
F
=
组间方差
组内方差
F = \frac{\text{组间方差}}{\text{组内方差}}
F=组内方差组间方差
其中:
- 组间方差衡量各组均值之间的差异
- 组内方差衡量各组内部的数据差异
3.3 随机过程与随机模拟
随机过程
随机过程是指系统在不确定性影响下随时间演变的过程。常见的随机过程包括泊松过程和马尔科夫链。
1. 泊松过程
泊松过程用于描述随机事件在固定时间间隔内发生的次数。泊松过程的公式如下:
P
(
N
(
t
)
=
k
)
=
(
λ
t
)
k
e
−
λ
t
k
!
P(N(t) = k) = \frac{(\lambda t)^k e^{-\lambda t}}{k!}
P(N(t)=k)=k!(λt)ke−λt
其中:
- N ( t ) N(t) N(t) 表示在时间 t t t 内发生的事件次数
- λ \lambda λ 是单位时间内发生事件的平均次数
- k k k 是事件发生的次数
2. 马尔科夫链
马尔科夫链用于描述系统从一个状态转移到另一个状态的过程,且当前状态只依赖于前一状态。状态转移矩阵
P
P
P 定义了从状态
i
i
i 转移到状态
j
j
j 的概率
P
i
j
P_{ij}
Pij。
随机模拟
随机模拟是利用随机数来模拟复杂系统的行为和性能。常见的随机模拟方法包括蒙特卡罗模拟。
1. 蒙特卡罗模拟
蒙特卡罗模拟通过大量随机样本的计算来估计系统的特性。例如,估计圆周率
π
\pi
π 的值,可以通过在单位正方形内生成随机点,并计算落在单位圆内的点的比例来实现。
import numpy as np
# 生成随机点
n_points = 10000
points = np.random.rand(n_points, 2)
# 计算落在单位圆内的点的数量
inside_circle = np.sum(np.sum(points**2, axis=1) <= 1)
# 估计π的值
pi_estimate = (inside_circle / n_points) * 4
print(f"Estimated value of π: {pi_estimate}")
通过上述方法和公式,可以更好地理解和应用统计分析模型,从而提高数据分析的效果。
simpy 实现随机过程仿真
使用 simpy 实现随机过程仿真通常包括以下几个步骤:
-
导入库:
- 导入
simpy以及其他可能需要的库(如numpy)。
- 导入
-
创建环境:
- 创建一个
simpy.Environment实例。
- 创建一个
-
定义资源和过程:
- 使用
simpy.Resource或simpy.Container创建仿真所需的资源。 - 定义仿真过程中使用的函数或生成器函数。
- 使用
-
设置过程行为:
- 在生成器函数中定义事件的行为和时间间隔,使用
env.timeout实现等待,使用yield关键字调度事件。
- 在生成器函数中定义事件的行为和时间间隔,使用
-
启动过程:
- 使用
env.process方法启动一个或多个过程。
- 使用
-
运行仿真:
- 使用
env.run方法运行仿真,直到指定的时间或事件。
- 使用
simpy.Environment 方法详细介绍
simpy.Environment 是 simpy 库中的核心类,用于创建和管理模拟环境。以下是 simpy.Environment 类的一些重要方法及其介绍:
-
__init__(self, initial_time=0):- 构造方法,创建一个新的仿真环境。
initial_time:仿真开始时的时间,默认为 0。
-
run(self, until=None):- 运行仿真环境,直到没有事件或达到指定的时间。
until:仿真结束的时间或事件。如果为 None,则仿真直到没有事件为止。
-
timeout(self, delay):- 创建一个延迟事件,表示经过一定的时间。
delay:延迟的时间。
-
process(self, generator):- 启动一个新的进程。
generator:生成器函数,定义进程的行为。
-
event(self):- 创建一个新的事件。
-
interrupt(self, cause=None):- 中断当前进程。
cause:中断的原因。
-
peek(self):- 返回下一个事件的时间。
-
step(self):- 执行下一个事件。
-
now:- 返回当前仿真时间。
案例1: 随机模拟车流量
为了改善道路的路面情况(道路经常维修,坑坑洼洼),因此想统计一天中有多少车辆经过,因为每天的车辆数都是随机的,一般来说有两种技术解决这个问题:
(1) 在道路附近安装一个计数器或安排一个技术人员,在一段长时间的天数(如365天)每天24h统计通过道路的车辆数。
(2) 使用仿真技术大致模拟下道路口的场景,得出一个近似可用的仿真统计指标。
由于方案(1)需要花费大量的人力物力以及需要花费大量的调研时间,虽然能得出准确的结果,但是有时候在工程应用中并不允许。因此,我们选择方案(2),我们通过一周的简单调查,得到每天的每个小时平均车辆数:[30, 20, 10, 6, 8, 20, 40, 100, 250, 200, 100, 65, 100, 120, 100, 120, 200, 220, 240, 180, 150, 100, 50, 40],通过利用平均车辆数进行仿真。
以下演示如何使用 simpy 实现随机过程仿真,即模拟车辆通过一个道路口的泊松过程:
import simpy
import numpy as np
class Road_Crossing:
def __init__(self, env):
self.road_crossing_container = simpy.Container(env, capacity=1e8, init=0)
def come_across(env, road_crossing, lmd):
while True:
body_time = np.random.exponential(1.0 / (lmd / 60)) # 生成一个指数分布的时间间隔
yield env.timeout(body_time) # 经过body_time个时间
yield road_crossing.road_crossing_container.put(1) # 增加一个车辆通过
hours = 24 # 一天24小时
days = 3 # 模拟3天
lmd_ls = [30, 20, 10, 6, 8, 20, 40, 100, 250, 200, 100, 65, 100, 120, 100, 120, 200, 220, 240, 180, 150, 100, 50, 40] # 每小时平均车辆通过数
car_sum = [] # 存储每一天的车辆总数
print('仿真开始:')
for day in range(days):
day_car_sum = 0 # 每天的车辆总数初始化为0
for hour, lmd in enumerate(lmd_ls):
env = simpy.Environment()
road_crossing = Road_Crossing(env)
env.process(come_across(env, road_crossing, lmd))
env.run(until=60) # 每次仿真60分钟
if hour % 4 == 0:
print("第" + str(day + 1) + "天,第" + str(hour + 1) + "时的车辆数:", road_crossing.road_crossing_container.level)
day_car_sum += road_crossing.road_crossing_container.level
car_sum.append(day_car_sum)
print("每天通过交通路口的车辆数之和为:", car_sum)
代码详解
-
导入库:
import simpy import numpy as np -
定义
Road_Crossing类:class Road_Crossing: def __init__(self, env): self.road_crossing_container = simpy.Container(env, capacity=1e8, init=0)
capacity=1e8设置容器的最大容量为1e8(非常大,实际模拟中不会达到这个值)。init=0设置容器的初始资源数量为 0,即初始时通过路口的车辆数为 0。
- 定义车辆到达过程:
def come_across(env, road_crossing, lmd): while True: body_time = np.random.exponential(1.0 / (lmd / 60)) # 生成一个指数分布的时间间隔 yield env.timeout(body_time) # 模拟车辆经过时间间隔 yield road_crossing.road_crossing_container.put(1) # 增加一个车辆通过
在 come_across 函数中,每辆车到达的时间间隔 body_time 是从指数分布中生成的随机数
然后通过 yield env.timeout(body_time) 模拟这段时间的经过
接着通过 yield road_crossing.road_crossing_container.put(1) 将车辆数量增加 1。
4. 设置仿真参数:
hours = 24 # 一天24小时
days = 3 # 模拟3天
lmd_ls = [30, 20, 10, 6, 8, 20, 40, 100, 250, 200, 100, 65, 100, 120, 100, 120, 200, 220, 240, 180, 150, 100, 50, 40] # 每小时平均车辆通过数
car_sum = [] # 存储每一天的车辆总数
- 运行仿真:
print('仿真开始:') for day in range(days): day_car_sum = 0 # 每天的车辆总数初始化为0 for hour, lmd in enumerate(lmd_ls): env = simpy.Environment() road_crossing = Road_Crossing(env) env.process(come_across(env, road_crossing, lmd)) env.run(until=60) # 每次仿真60分钟 if hour % 4 == 0: print("第" + str(day + 1) + "天,第" + str(hour + 1) + "时的车辆数:", road_crossing.road_crossing_container.level) day_car_sum += road_crossing.road_crossing_container.level car_sum.append(day_car_sum) print("每天通过交通路口的车辆数之和为:", car_sum)
在主循环中,通过 road_crossing.road_crossing_container.level 获取当前时间段内通过路口的车辆总数,并累加到每日的车辆总数:
案例2: 随机模拟商店营业额
仿真“每天的商店营业额”这个复合泊松过程。首先,我们假设每个小时进入商店的平均人数为:[10, 5, 3, 6, 8, 10, 20, 40, 100, 80, 40, 50, 100, 120, 30, 30, 60, 80, 100, 150, 70, 20, 20, 10],每位顾客的平均花费为:10元(大约一份早餐吧),请问每天商店的营业额是多少?
# 模拟仿真研究该商店一天的营业额
import simpy
class Store_Money:
def __init__(self, env):
self.store_money_container = simpy.Container(env, capacity = 1e8, init = 0)
def buy(env, store_money, lmd, avg_money):
while True:
body_time = np.random.exponential(1.0/(lmd/60)) # 经过指数分布的时间后,泊松过程记录数+1
yield env.timeout(body_time)
money = np.random.poisson(lam=avg_money)
yield store_money.store_money_container.put(money)
hours = 24 # 一天24h
minutes = 60 # 一个小时60min
days = 3 # 模拟3天
avg_money = 10
lmd_ls = [10, 5, 3, 6, 8, 10, 20, 40, 100, 80, 40, 50, 100, 120, 30, 30, 60, 80, 100, 150, 70, 20, 20, 10] # 每个小时平均进入商店的人数
money_sum = [] # 存储每一天的商店营业额总和
print('仿真开始:')
for day in range(days):
day_money_sum = 0 # 记录每天的营业额之和
for hour, lmd in enumerate(lmd_ls):
env = simpy.Environment()
store_money = Store_Money(env)
store_money_process = env.process(buy(env, store_money, lmd, avg_money))
env.run(until = 60) # 每次仿真60min
if hour % 4 == 0:
print("第"+str(day+1)+"天,第"+str(hour+1)+"时的营业额:", store_money.store_money_container.level)
day_money_sum += store_money.store_money_container.level
money_sum.append(day_money_sum)
print("每天商店的的营业额之和为:", money_sum)
案例1和案例2的区别是,案例2中多了金额这一个泊松分布因子,因此在创建模型时加入money = np.random.poisson(lam=avg_money)
案例3: 随机模拟病毒状态转移
艾滋病发展过程分为四个阶段(状态),急性感染期(状态 1)、无症状期(状态 2), 艾滋病前期(状态 3), 典型艾滋病期(状态 4)。艾滋病发展过程基本上是一个不可逆的过程,即:状态1 -> 状态2 -> 状态3 -> 状态4。现在收集某地600例艾滋病防控数据,得到以下表格:
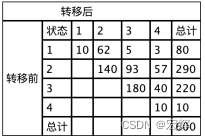
现在,我们希望计算若一个人此时是无症状期(状态2)在10次转移之后,这个人的各状态的概率是多少?
以下代码用于计算艾滋病患者在无症状期(状态2)经过10次转移后各个状态的概率分布。
示例代码
import numpy as np
# 初始状态向量,表示病人当前在无症状期(状态2)
p0 = np.array([0, 1, 0, 0])
# 状态转移矩阵
P = np.array([
[10.0/80, 62.0/80, 5.0/80, 3.0/80], # 从状态1转移到各状态的概率
[0, 140.0/290, 93.0/290, 57.0/290], # 从状态2转移到各状态的概率
[0, 0, 180.0/220, 40.0/220], # 从状态3转移到各状态的概率
[0, 0, 0, 1] # 从状态4转移到各状态的概率(状态4为终止状态)
])
# 转移次数
N = 10
# 计算10次转移后的状态分布
print(str(N) + "期转移后,状态分布为:", np.round(get_years_dist(p0, P, N), 4))
输出结果
10期转移后,状态分布为: [0.000e+00 3.000e-04 1.048e-01 8.948e-01]
结果解释
经过10次转移后,一个初始状态在无症状期(状态2)的患者,最终各个状态的概率分布为:
- 急性感染期(状态1):概率为0.0000,即几乎不可能回到状态1。
- 无症状期(状态2):概率为0.0003,即很小的概率仍在状态2。
- 艾滋病前期(状态3):概率为0.1048,即大约10.48%的概率处于状态3。
- 典型艾滋病期(状态4):概率为0.8948,即大约89.48%的概率已经进入状态4。
这种转移概率的计算过程利用了马尔科夫链模型,通过多次矩阵乘法来模拟状态的转移过程。
代码解释
1)函数定义
def get_years_dist(p0, P, N):
这行代码定义了一个名为 get_years_dist 的函数。这个函数有三个参数:
p0:初始状态向量,表示病人当前在某个状态的概率分布。P:状态转移矩阵,表示从一个状态转移到另一个状态的概率。N:转移次数,表示经过多少次转移。
2)初始化状态转移矩阵
P1 = P
将 P 矩阵赋值给 P1,准备对 P1 进行后续的多次矩阵乘法操作。
3)进行N次转移
for i in range(N):
P1 = np.matmul(P1, P)
使用循环进行N次状态转移。np.matmul(P1, P) 进行矩阵乘法,将 P1 矩阵与 P 矩阵相乘。每次循环,P1 都会更新为上一次的乘积结果。
4)计算最终状态分布
return np.matmul(p0, P1)
在进行完N次转移后,将初始状态向量 p0 与最终的状态转移矩阵 P1 相乘,得到经过N次转移后的状态分布。
4. 数据可视化
4.1 Python三大数据可视化工具库的简介
(1)Matplotlib:
Matplotlib脱胎于著名的建模软件Matlab,因此它的设计与Matlab非常相似,提供了一整套和Matlab相似的命令API,适合交互式制图,还可以将它作为绘图控件,嵌入其它应用程序中。同时,Matplotlib是Python数据可视化工具库的开山鼻祖。
Matplotlib是一个面向对象的绘图工具库,pyplot是Matplotlib最常用的一个绘图接口,调用方法如下:
import matplotlib.pyplot as plt
在Matplotlib中,我们可以想像自己手里拿着一支画笔🖌️,每一句代码都是往纸上添加一个绘图特征,下面我们以最简单的方式绘制散点图为例:
- 创建一个图形对象,并设置图形对象的大小:
plt.figure(figsize=(6,4)) - 在纸上的坐标系中绘制散点:
plt.scatter(x=x, y=y) - 设置x轴的标签label:
plt.xlabel('x') - 设置y轴标签的label:
plt.ylabel('y') - 设置图表的标题:
plt.title('y = sin(x)') - 展示图表:
plt.show()
举个例子:
# 创建数据
x = np.linspace(-2*np.pi, 2*np.pi, 100)
y = np.sin(x)
import matplotlib.pyplot as plt
plt.figure(figsize=(8,6))
plt.scatter(x=x, y=y)
plt.xlabel('x')
plt.ylabel('y')
plt.title('y = sin(x)')
plt.show()
在上面的例子中,我们通过Matplotlib绘制了最简单的散点图,但是以上的方法没有体现Matplotlib的“面向对象”的特性。下面,我们使用一个例子体会Matplotlib的面向对象绘图的特性:
【例子】绘制y = sin(x) 和 y=cos(x)的散点图:
# 准备数据
x = np.linspace(-2*np.pi, 2*np.pi, 100)
y1 = np.sin(x)
y2 = np.cos(x)
# 绘制第一个图:
fig1 = plt.figure(figsize=(6,4), num='first')
fig1.suptitle('y = sin(x)')
plt.scatter(x=x, y=y1)
plt.xlabel('x')
plt.ylabel('y')
# 绘制第二个图:
fig2 = plt.figure(figsize=(6,4), num='second')
fig2.suptitle('y = cos(x)')
plt.scatter(x=x, y=y2)
plt.xlabel('x')
plt.ylabel('y')
plt.show()
现在,大家应该能体会到“Matplotlib的每一句代码都是往纸上添加一个绘图特征”这句话的含义了吧。现在,我们来看看这样的Matplotlib有什么优点与缺点。优点是非常简单易懂,而且能绘制复杂图表;缺点也是十分明显的,如果绘制复杂图表的时候一步一步地绘制,代码量还是十分巨大的。Seaborn是在Matplotlib的基础上的再次封装,是对Matplotlib绘制统计图表的简化。下面,我们一起看看Seaborn的基本绘图逻辑。
(2)Seaborn:
Seaborn主要用于统计分析绘图的,它是基于Matplotlib进行了更高级的API封装。Seaborn比matplotlib更加易用,尤其在统计图表的绘制上,因为它避免了matplotlib中多种参数的设置。Seaborn与matplotlib关系,可以把Seaborn视为matplotlib的补充。
下面,我们使用一个简单的例子,来看看使用Seaborn绘图与使用Matplotlib绘图之间的代码有什么不一样:
# 准备数据
x = np.linspace(-10, 10, 100)
y = 2 * x + 1 + np.random.randn(100)
df = pd.DataFrame({'x':x, 'y':y})
# 使用Seaborn绘制带有拟合直线效果的散点图
sns.lmplot("x","y",data=df)
可以看到,Seaborn把数据拟合等统计属性高度集成在绘图函数中,绘图的功能还是构筑在Matplotlib之上。因此,Seaborn相当于是完善了统计图表的Matplotlib工具库,二者应该是相辅相成的。因此,在实际的可视化中,我们往往一起使用Matplotlib和Seaborn,两者的结合应该属于Python的数据可视化的一大流派吧。
(3)Plotnine:
ggplot2奠定了R语言数据可视化在R语言数据科学的统治地位,R语言的数据可视化是大一统的,提到R语言数据可视化首先想到的就是ggplot2。数据可视化一直是Python的短板,即使有Matplotlib、Seaborn等数据可视化包,也无法与R语言的ggplot2相媲美,原因在于当绘制复杂图表时,Matplotlib和Seaborn由于“每一句代码都是往纸上添加一个绘图特征”的特性而需要大量代码语句。Plotnine可以说是ggplot2在Python上的移植版,使用的基本语法与R语言ggplot2语法“一模一样”,使得Python的数据可视化能力大幅度提升,为什么ggplot2和Plotnine会更适合数据可视化呢?原因可以类似于PhotoShop绘图和PPT绘图的区别,与PPT一笔一画的绘图方式不同的是,PhotoShop绘图采用了“图层”的概念,每一句代码都是相当于往图像中添加一个图层,一个图层就是一类绘图动作,这无疑给数据可视化工作大大减负,同时更符合绘图者的认知。
下面,我们通过一个案例来看看Plotnine的图层概念以及Plotnine的基本绘图逻辑:
from plotnine import * # 将Plotnine所有模块引入
from plotnine.data import mpg # 引入Plotnine自带数据集
mpg.head()
mpg数据集记录了美国1999年和2008年部分汽车的制造厂商,型号,类别,驱动程序和耗油量。
# 绘制汽车在不同驱动系统下,发动机排量与耗油量的关系
p1 = (
ggplot(mpg, aes(x='displ', y='hwy', color='drv')) # 设置数据映射图层,数据集使用mpg,x数据使用mpg['displ'],y数据使用mpg['hwy'],颜色映射使用mog['drv']
+ geom_point() # 绘制散点图图层
+ geom_smooth(method='lm') # 绘制平滑线图层
+ labs(x='displacement', y='horsepower') # 绘制x、y标签图层
)
print(p1) # 展示p1图像
从上面的案例,我们可以看到Plotnine的绘图逻辑是:一句话一个图层。因此,在Plotnine中少量的代码就能画图非常漂亮的图表,而且可以画出很多很复杂的图表,就类似于PhotoShop能轻松画出十分复杂的图但是PPT需要大量时间也不一定能达到同样的效果。
那什么时候选择Matplotlib、Seaborn还是Plotnine?Plotnine具有ggplot2的图层特性,但是由于开发时间较晚,目前这个工具包还有一些缺陷,其中最大的缺陷就是:没有实现除了直角坐标以外的坐标体系,如:极坐标。因此,Plotnine无法绘制类似于饼图、环图等图表。为了解决这个问题,在绘制直角坐标系的图表时,我们可以使用Plotnine进行绘制,当涉及极坐标图表时,我们使用Matplotlib和Seaborn进行绘制。有趣的是,Matplotlib具有ggplot风格,可以通过设置ggplot风格绘制具有ggplot风格的图表。
plt.style.use("ggplot") # 风格使用ggplot
但是值得注意的是,这里所说的绘制ggplot风格,是看起来像ggplot表格,但是实际上Matplotlib还是不具备图层风格。
4.2 基本图表Quick Start
(1)类别型图表:类别型图表一般表现为:X类别下Y数值之间的比较,因此类别型图表往往包括:X为类别型数据、Y为数值型数据。类别型图表常常有:柱状图、横向柱状图(条形图)、堆叠柱状图、极坐标的柱状图、词云、雷达图、桑基图等等。
## Matplotlib绘制单系列柱状图:不同城市的房价对比
data = pd.DataFrame({'city':['深圳', '上海', '北京', '广州', '成都'], 'house_price(w)':[
1100, 950, 900, 450, 400]})
plt.figure(figsize=(8,6))
plt.bar(data['city'], data['house_price(w)'])
plt.xlabel('City')
plt.ylabel('House Price(w)')
plt.title('House Price in Different City')
plt.show()
【例子】Seaborn绘制堆叠柱状图(barplot):不同城市,不同年房价对比:
data = pd.DataFrame({
'city':['深圳', '深圳', '深圳', '上海', '上海', '上海', '北京', '北京', '北京', '广州', '广州', '广州', '成都', '成都', '成都'],
'house_price(w)':[1100, 1080, 1050, 950, 900, 880, 900, 860, 810, 450, 460, 470, 400, 380, 370],
'year':['2020', '2021', '2022', '2020', '2021', '2022', '2020', '2021', '2022', '2020', '2021', '2022', '2020', '2021', '2022']
})
plt.figure(figsize=(8,6))
sns.barplot(x='city', y='house_price(w)', hue='year', data=data)
plt.xlabel('City')
plt.ylabel('House Price(w)')
plt.title('House Price in Different City in Different Year')
plt.show()
【例子】Seaborn绘制极坐标的柱状图:
# 设置数据
values=[4, 3, 4, 5, 4, 4, 3]
labels=['A', 'B', 'C', 'D', 'E', 'F', 'G']
# 设置绘图风格
plt.style.use("ggplot")
fig = plt.figure(figsize=(6,6))
# 绘制极坐标
ax = fig.add_subplot(111, polar=True)
ax.bar(range(7), values, tick_label=labels)
plt.show()
【例子】WordCloud绘制词云图:
from wordcloud import WordCloud
import matplotlib.pyplot as plt
# 生成词云
wordcloud = WordCloud().generate('Python data visualization with matplotlib seaborn and plotnine')
# 绘制词云
plt.imshow(wordcloud, interpolation='bilinear')
plt.axis("off")
plt.show()
从上面我们可以看出Matplotlib、Seaborn等工具库都能绘制出类别型的图表,但是Seaborn更加简洁,Plotnine绘制的词云图更具艺术性(更复杂的词云图可以通过样式图等来设置样式)。
(2)时间序列图表:时间序列图表表现为:X时间下Y数值之间的关系,因此时间序列图表往往包括:X为时间型数据、Y为数值型数据。时间序列图表常常有:折线图、面积图、堆叠面积图、双轴图表、横向折线图、极坐标的时间序列图表、时间序列的堆积柱状图等。
【例子】Matplotlib绘制时间序列图表(单系列折线图):最近20天的累计销售额:
# 准备数据
date = pd.date_range(start='2020-01-01', periods=20)
sales = np.random.randint(100, 200, 20)
data = pd.DataFrame({'date':date, 'sales':sales})
# 绘制折线图
plt.figure(figsize=(8,6))
plt.plot(data['date'], data['sales'])
plt.xlabel('Date')
plt.ylabel('Sales')
plt.title('Daily Sales Over Time')
plt.xticks(rotation=45)
plt.show()
【例子】Plotnine绘制时间序列的堆积面积图:
# 准备数据
date = pd.date_range(start='2020-01-01', periods=20)
sales_a = np.random.randint(100, 200, 20)
sales_b = np.random.randint(50, 100, 20)
data = pd.DataFrame({'date':date, 'sales_a':sales_a, 'sales_b':sales_b})
# 绘制堆积面积图
p = (
ggplot(data, aes(x='date'))
+ geom_area(aes(y='sales_a'), fill='blue', alpha=0.5)
+ geom_area(aes(y='sales_b'), fill='red', alpha=0.5)
+ labs(x='Date', y='Sales')
)
print(p)
【例子】Matplotlib绘制时间序列的极坐标图表:
# 设置数据
date = pd.date_range(start='2020-01-01', periods=20)
sales = np.random.randint(100, 200, 20)
data = pd.DataFrame({'date':date, 'sales':sales})
# 设置绘图风格
plt.style.use("ggplot")
fig = plt.figure(figsize=(6,6))
# 绘制极坐标
ax = fig.add_subplot(111, polar=True)
ax.plot(range(20), data['sales'])
plt.show()
从上面可以看出,Matplotlib绘制的时间序列图表更加灵活,Seaborn和Plotnine也能绘制出时间序列图表,但是可能灵活性和细节方面稍差一些。
(3)关联性图表:关联性图表表现为:X数值与Y数值之间的关系,或者两个类别变量之间的关系,因此关联性图表往往包括:X为数值型数据、Y为数值型数据。关联性图表常常有:散点图、热力图、关系网络图等。
【例子】Matplotlib绘制关联性图表:两个变量之间的关系(散点图):
# 准备数据
x = np.random.randn(100)
y = 2 * x + 1 + np.random.randn(100)
# 绘制散点图
plt.figure(figsize=(8,6))
plt.scatter(x, y)
plt.xlabel('X')
plt.ylabel('Y')
plt.title('Scatter Plot of X vs Y')
plt.show()
【例子】Seaborn绘制关联性图表(热力图):两个类别变量之间的关系(相关性矩阵):
# 准备数据
data = np.random.rand(10, 12)
# 绘制热力图
plt.figure(figsize=(8,6))
sns.heatmap(data, annot=True, fmt=".2f")
plt.xlabel('Variable 1')
plt.ylabel('Variable 2')
plt.title('Heatmap of Variable 1 vs Variable 2')
plt.show()
【例子】Plotnine绘制关联性图表(散点图与拟合直线图层):
# 准备数据
x = np.random.randn(100)
y = 2 * x + 1 + np.random.randn(100)
data = pd.DataFrame({'x':x, 'y':y})
# 绘制散点图与拟合直线
p = (
ggplot(data, aes(x='x', y='y'))
+ geom_point()
+ geom_smooth(method='lm')
+ labs(x='X', y='Y')
)
print(p)
从上面可以看出,Matplotlib、Seaborn和Plotnine都可以绘制关联性图表,但是Matplotlib的绘制更加灵活,Seaborn和Plotnine在特定图表上有更高效的接口。
综上所述,Matplotlib适用于各种图表的绘制,灵活性较强,Seaborn在绘制统计图表时有较简洁的API,Plotnine在绘制基于图层概念的复杂图表时非常高效。因此,在实际数据可视化工作中,可以根据具体的需求选择适合的工具库,灵活运用它们的特点,打造出专业而美观的图表。
5. 插值模型
5.1 线性插值法
线性插值法在两个已知数据点之间进行线性插值,假设在两个点之间,数据变化是线性的。
公式
对于两个数据点 ( x 0 , y 0 ) (x_0, y_0) (x0,y0) 和 ( x 1 , y 1 ) (x_1, y_1) (x1,y1),线性插值的公式为:
y = y 0 + ( y 1 − y 0 ) ( x 1 − x 0 ) ⋅ ( x − x 0 ) y = y_0 + \frac{(y_1 - y_0)}{(x_1 - x_0)} \cdot (x - x_0) y=y0+(x1−x0)(y1−y0)⋅(x−x0)
代码示例
import numpy as np
import matplotlib.pyplot as plt
import scipy.interpolate as spi
# 定义样本点
X = np.arange(-2 * np.pi, 2 * np.pi, 1)
Y = np.sin(X)
# 定义插值点
new_x = np.arange(-2 * np.pi, 2 * np.pi, 0.1)
# 进行一阶样条插值
linear_ipol = spi.splrep(X, Y, k=1)
linear_iyl = spi.splev(new_x, linear_ipol)
# 画出插值前和插值后的数据
plt.figure(figsize=(10, 6))
plt.plot(X, Y, 'o', label='Original data')
plt.plot(new_x, linear_iyl, '-', label='Linear Interpolated data')
plt.legend()
plt.title('Linear Interpolation of sin(x)')
plt.xlabel('x')
plt.ylabel('sin(x)')
plt.show()
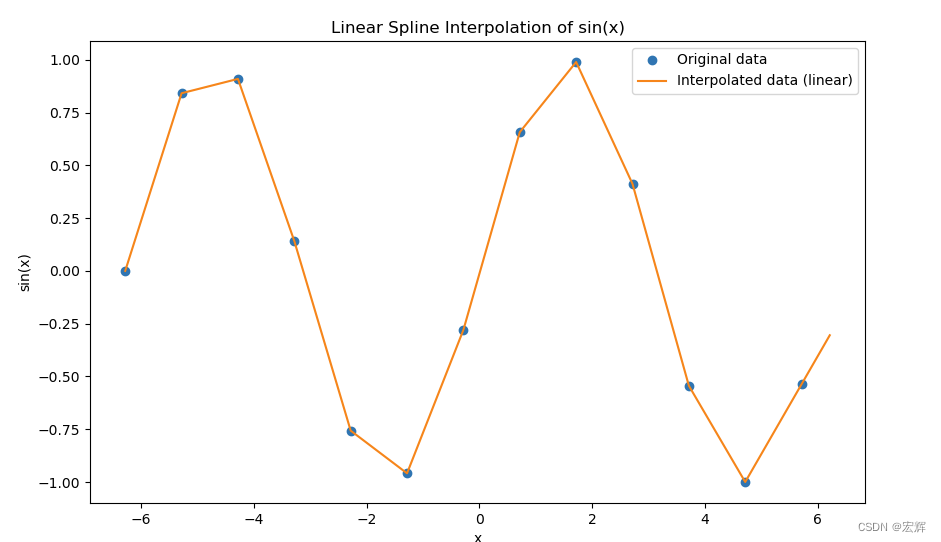
5.2 三次样条插值
三次样条插值在每个区间上使用三次多项式来进行插值,并确保插值函数在每个区间的端点处一阶和二阶导数连续。
公式
对于区间 [ x i , x i + 1 ] [x_i, x_{i+1}] [xi,xi+1] 上的三次样条插值,插值多项式为:
S i ( x ) = a i + b i ( x − x i ) + c i ( x − x i ) 2 + d i ( x − x i ) 3 S_i(x) = a_i + b_i(x - x_i) + c_i(x - x_i)^2 + d_i(x - x_i)^3 Si(x)=ai+bi(x−xi)+ci(x−xi)2+di(x−xi)3
三次样条插值需要满足以下条件:
- 在每个插值点处,插值多项式的值等于数据点的值。
- 在每个插值点处,插值多项式的一阶导数和二阶导数连续。
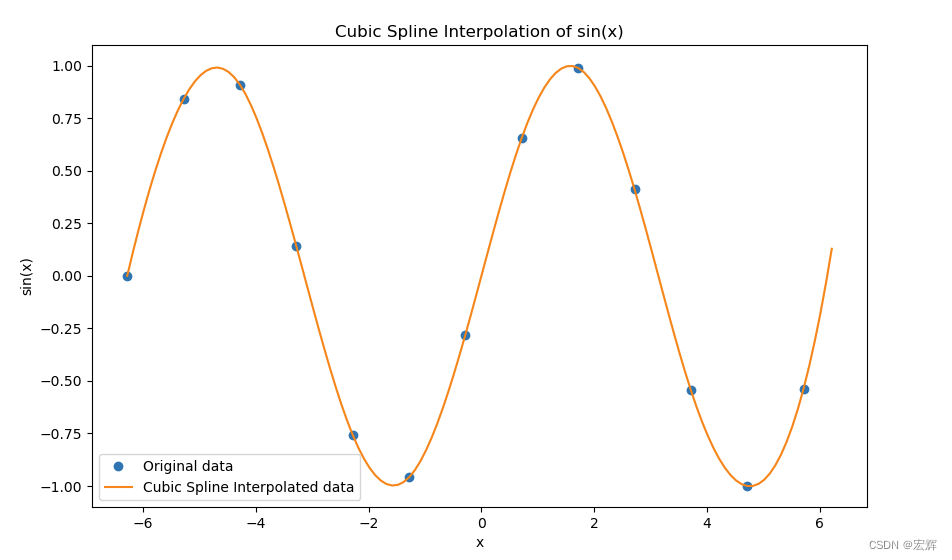
代码示例
# 进行三次样条插值
cubic_ipol = spi.splrep(X, Y, k=3)
cubic_iyl = spi.splev(new_x, cubic_ipol)
# 画出插值前和插值后的数据
plt.figure(figsize=(10, 6))
plt.plot(X, Y, 'o', label='Original data')
plt.plot(new_x, cubic_iyl, '-', label='Cubic Spline Interpolated data')
plt.legend()
plt.title('Cubic Spline Interpolation of sin(x)')
plt.xlabel('x')
plt.ylabel('sin(x)')
plt.show()
5.3 拉格朗日插值
拉格朗日插值通过构造一个多项式,使得多项式在每个已知数据点处的值等于该点的值。
公式
拉格朗日插值多项式为:
P ( x ) = ∑ i = 0 n y i ∏ j = 0 , j ≠ i n x − x j x i − x j P(x) = \sum_{i=0}^{n} y_i \prod_{j=0, j \neq i}^{n} \frac{x - x_j}{x_i - x_j} P(x)=i=0∑nyij=0,j=i∏nxi−xjx−xj
代码示例
import scipy.interpolate as spi
# 进行拉格朗日插值
lagrange_ipol = spi.lagrange(X, Y)
lagrange_iyl = lagrange_ipol(new_x)
# 画出插值前和插值后的数据
plt.figure(figsize=(10, 6))
plt.plot(X, Y, 'o', label='Original data')
plt.plot(new_x, lagrange_iyl, '-', label='Lagrange Interpolated data')
plt.legend()
plt.title('Lagrange Interpolation of sin(x)')
plt.xlabel('x')
plt.ylabel('sin(x)')
plt.show()

分析插值效果
- 线性插值:在两个相邻数据点之间进行线性连接,效果较为粗糙,但计算简单。
- 三次样条插值:在每个区间使用三次多项式插值,保证了插值函数的连续性和平滑性,效果较好。
- 拉格朗日插值:通过构造一个全局多项式进行插值,能够很好地通过所有数据点,但在数据点较多时可能出现震荡现象(龙格现象)。
通过可视化对比可以发现,三次样条插值和拉格朗日插值在平滑度和准确性上优于线性插值。
6. 知识拓展
6.1 指数分布与泊松分布的关系和区别
np.random.exponential 和 np.random.poisson 是 numpy 库中的两个函数,用于生成符合指数分布和泊松分布的随机数。它们分别用于模拟连续时间间隔和离散事件的发生。下面详细介绍它们的关系和区别。
指数分布与泊松分布的关系
- 泊松过程:泊松过程是描述随机事件在时间或空间上发生的模型。泊松过程的一个重要特性是时间间隔符合指数分布。
- 指数分布:用于描述两个连续事件发生的时间间隔。假设事件发生的平均速率为 (\lambda),则时间间隔 (t) 的概率密度函数为 (f(t) = \lambda e^{-\lambda t})。
- 泊松分布:用于描述在固定时间间隔内发生的事件数。假设单位时间内事件的平均发生次数为 (\lambda),则在时间间隔 (t) 内发生 (k) 次事件的概率为 (P(X=k) = \frac{(\lambda t)^k e^{-\lambda t}}{k!})。
总结来说,泊松过程中的事件时间间隔服从指数分布,而在固定时间间隔内事件发生次数服从泊松分布。
np.random.exponential
np.random.exponential(scale, size=None) 用于生成符合指数分布的随机数。
-
scale:指数分布的尺度参数,即 ( \frac{1}{\lambda} )。 -
size:生成的样本数量。 -
示例
import numpy as np
# 生成10个符合指数分布的随机数,λ = 2, 则 scale = 1/λ = 0.5
exp_samples = np.random.exponential(scale=0.5, size=10)
print(exp_samples)
np.random.poisson
np.random.poisson(lam, size=None) 用于生成符合泊松分布的随机数。
-
lam:泊松分布的参数,即单位时间内事件的平均发生次数 (\lambda)。 -
size:生成的样本数量。 -
示例
import numpy as np
# 生成10个符合泊松分布的随机数,λ = 3
poisson_samples = np.random.poisson(lam=3, size=10)
print(poisson_samples)
指数分布与泊松分布的区别
-
用途:
np.random.exponential用于生成连续时间间隔的随机数,模拟事件发生的时间间隔。np.random.poisson用于生成离散事件数的随机数,模拟固定时间间隔内的事件发生次数。
-
参数:
np.random.exponential的参数是scale,对应指数分布的尺度参数(平均时间间隔的倒数)。np.random.poisson的参数是lam,对应单位时间内事件的平均发生次数。
-
分布性质:
- 指数分布是连续分布,用于描述事件发生的时间间隔。
- 泊松分布是离散分布,用于描述在固定时间间隔内的事件发生次数。
画图

def plot_pic():
# 设置绘图风格
sns.set(style="whitegrid")
# 参数
lambda_poisson = 5 # 泊松分布参数,单位时间内事件的平均发生次数
lambda_exponential = 5 # 指数分布参数,单位时间内事件的平均发生次数的倒数
# 生成泊松分布数据
poisson_data = np.random.poisson(lam=lambda_poisson, size=1000)
# 生成指数分布数据
exponential_data = np.random.exponential(scale=1.0 / lambda_exponential, size=1000)
# 创建图形
fig, axs = plt.subplots(1, 2, figsize=(14, 6))
# 绘制泊松分布直方图
sns.histplot(poisson_data, bins=range(0, 20), kde=False, ax=axs[0], color='blue')
axs[0].set_title('Poisson Distribution (λ={})'.format(lambda_poisson))
axs[0].set_xlabel('Number of events')
axs[0].set_ylabel('Frequency')
# 绘制指数分布直方图
sns.histplot(exponential_data, bins=50, kde=True, ax=axs[1], color='red')
axs[1].set_title('Exponential Distribution (λ={})'.format(lambda_exponential))
axs[1].set_xlabel('Time between events')
axs[1].set_ylabel('Frequency')
# 显示图形
plt.tight_layout()
plt.show()
6.2 马尔可夫链 (Markov Chain)
马尔可夫链是一种随机过程,它满足“马尔可夫性质”,即未来状态仅依赖于当前状态,而与过去的状态无关。这种性质使得马尔可夫链在各种领域中应用广泛,如经济学、物理学、计算机科学等。
定义
马尔可夫链由一组状态 S = { s 1 , s 2 , … , s n } S = \{s_1, s_2, \ldots, s_n\} S={s1,s2,…,sn} 和状态转移概率矩阵 P P P 组成,矩阵 P P P 描述了从一个状态转移到另一个状态的概率。
状态转移概率矩阵 P P P 的元素 p i j p_{ij} pij 表示从状态 s i s_i si 转移到状态 s j s_j sj 的概率:
P = [ p 11 p 12 ⋯ p 1 n p 21 p 22 ⋯ p 2 n ⋮ ⋮ ⋱ ⋮ p n 1 p n 2 ⋯ p n n ] P = \begin{bmatrix} p_{11} & p_{12} & \cdots & p_{1n} \\ p_{21} & p_{22} & \cdots & p_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ p_{n1} & p_{n2} & \cdots & p_{nn} \\ \end{bmatrix} P= p11p21⋮pn1p12p22⋮pn2⋯⋯⋱⋯p1np2n⋮pnn
满足条件:
∑ j = 1 n p i j = 1 , ∀ i \sum_{j=1}^{n} p_{ij} = 1, \quad \forall i j=1∑npij=1,∀i
公式
给定当前状态 X t = s i X_t = s_i Xt=si,下一个状态 X t + 1 X_{t+1} Xt+1 的概率分布由状态转移概率矩阵决定:
P ( X t + 1 = s j ∣ X t = s i ) = p i j \mathbb{P}(X_{t+1} = s_j \mid X_t = s_i) = p_{ij} P(Xt+1=sj∣Xt=si)=pij
示例
我们以一个简单的天气模型为例,假设有三个状态:晴天(Sunny)、阴天(Cloudy)和雨天(Rainy)。状态转移概率矩阵如下:
P = [ 0.8 0.15 0.05 0.2 0.6 0.2 0.25 0.25 0.5 ] P = \begin{bmatrix} 0.8 & 0.15 & 0.05 \\ 0.2 & 0.6 & 0.2 \\ 0.25 & 0.25 & 0.5 \\ \end{bmatrix} P= 0.80.20.250.150.60.250.050.20.5
这意味着:
- 晴天转移到晴天的概率是 0.8,转移到阴天的概率是 0.15,转移到雨天的概率是 0.05。
- 阴天转移到晴天的概率是 0.2,转移到阴天的概率是 0.6,转移到雨天的概率是 0.2。
- 雨天转移到晴天的概率是 0.25,转移到阴天的概率是 0.25,转移到雨天的概率是 0.5。
代码示例
下面是一个用 Python 实现简单天气马尔可夫链的示例:
import numpy as np
# 定义状态
states = ["Sunny", "Cloudy", "Rainy"]
# 定义状态转移概率矩阵
P = np.array([[0.8, 0.15, 0.05],
[0.2, 0.6, 0.2],
[0.25, 0.25, 0.5]])
# 初始状态分布
initial_state = np.array([1.0, 0.0, 0.0]) # 从晴天开始
# 模拟马尔可夫链
n_steps = 10
current_state = initial_state
state_sequence = []
for _ in range(n_steps):
state_sequence.append(np.argmax(current_state))
current_state = np.dot(current_state, P)
# 打印状态序列
state_sequence = [states[i] for i in state_sequence]
print("State sequence: ", state_sequence)
# 可视化状态序列
import matplotlib.pyplot as plt
plt.figure(figsize=(10, 6))
plt.plot(range(n_steps), state_sequence, 'o-')
plt.yticks([0, 1, 2], states)
plt.xlabel("Time step")
plt.ylabel("State")
plt.title("Markov Chain State Sequence")
plt.grid(True)
plt.show()
在这段代码中,我们定义了状态和状态转移概率矩阵,然后通过循环迭代计算每一步的状态。在每一步中,我们将当前状态与状态转移矩阵相乘,以获得下一个状态的分布。最后,我们可视化了状态序列。
通过这个示例,我们可以看到马尔可夫链的工作原理,并理解其在模拟和预测中的应用。马尔可夫链在实际应用中可以处理更多状态和更复杂的转移矩阵,如用户行为预测、股票市场分析等。
7. 学习心得
在随机过程的学习中,深入了解了指数分布与泊松分布的关系和区别。
泊松过程中的事件时间间隔服从指数分布,而在固定时间间隔内事件发生次数服从泊松分布。指数分布是连续分布,用于描述事件发生的时间间隔。泊松分布是离散分布,用于描述在固定时间间隔内的事件发生次数。
使用simpy进行随机过程仿真,通过案例1随机模拟车流量掌握了simpy的基本使用,了解simpy库函数的基本功能。通过案例2计算营业额了解到符合泊松分布的处理逻辑。案例3则直接用马尔可夫链通过构建状态转移矩阵计算出N阶段后病毒状态转移的概率。
掌握了panda处理数据、使用Matplotlib、Seaborn、Plotnine分别对数据进行可视化,其中Matplotlib面向对象编程、Seaborn则是封装了Matplotlib,高度集成api让用户使用更便捷,Plotnine则是按图层出图。
对线性插值、三次样条插值和拉格朗日插值进行了模拟仿真,通过可视化对比发现:三次样条插值和拉格朗日插值在平滑度和准确性上优于线性插值。