文章目录
- 一、前言
- 二、问题
- 问题:1372. 活动选择
- 问题:1456. 淘淘捡西瓜
- 问题:1485. 接水问题
- 三、感谢
一、前言
本章节主要对贪心问题进行讲解,包括《1372. 活动选择》《1456. 淘淘捡西瓜》《1485. 接水问题》题目。
二、问题
问题:1372. 活动选择
类型:贪心
题目描述:
学校在最近几天有 n(n≤100)个活动,这些活动都需要使用学校的大礼堂,在同一时间,礼堂只能被一个活动使。由于有些活动时间上有冲突,学校办公室人员只好让一些活动放弃使用礼堂而使用其他教室。
现在给出 n 个活动使用礼堂的起始时间begini 和结束时间 endi (begini < endi),请你帮助办公室人员安排一些活动来使用礼堂,要求安排的活动尽量多。请问最多可以安排多少活动?
请注意,开始时间和结束时间均指的是某个小时的 0 分 0 秒,如:3 5,指的是 3:00~5:00 ,因此3 5和5 9这两个时间段不算冲突的时间段。
输入:
第一行一个整数 n (n≤100);
接下来的 n 行,每行两个整数,第一个 begini ,第二个是 endi (begini < endi ≤ 32767);
输出:
输出最多能安排的活动数;
样例:
输入:
11
3 5
1 4
12 14
8 12
0 6
8 11
6 10
5 7
3 8
5 9
2 13
输出:
4

1.分析问题
- 已知:有 n(n≤100)个活动, n 个活动使用礼堂的起始时间begini 和结束时间 endi (begini < endi)。
- 未知:请问最多可以安排多少活动?
- 关系:采用贪心策略,关键在于按活动的结束时间进行排序。
2.定义变量
//二、数据定义
int n,a[1010],b[1010],endi=0,c=0;
3.输入数据
//三、数据输入
cin>>n;
for(int i=0;i<n;i++){
cin>>a[i]>>b[i];
}
4.数据计算
- 使用冒泡排序算法对活动的结束时间进行升序排序。在交换结束时间的同时,同步交换对应的开始时间,以保持活动信息的完整性。
for(int i=0;i<n-1;i++){
for(int j=0;j<n-1-i;j++){
if(b[j]>=b[j+1]){
swap(b[j],b[j+1]);
//同步开始时间
swap(a[j],a[j+1]);
}
}
}
- 选择不冲突活动:遍历排序后的活动列表,如果当前活动的开始时间大于等于endi(即前一个活动的结束时间),说明当前活动可以安排,此时更新endi为当前活动的结束时间,并增加已安排活动计数器c。
for(int i=0;i<n;i++){
if(a[i]>=endi){
endi=b[i];
++c;
}
}
5.输出结果
- 输出最多能安排的活动数量。
cout << c << endl;
完整代码如下:
#include<bits/stdc++.h>
using namespace std;
int main(){
// 一、问题分析
// 给定多个活动,每个活动由起始时间和结束时间定义,要求计算并输出最多能安排多少个活动,
// 条件是活动不能同时进行,即一个活动开始时,前一个活动必须已经结束。
// 解决方案采用贪心策略,关键在于按活动的结束时间进行排序。
// 二、数据定义
int n; // 活动数量
int a[1010], b[1010]; // a[] 存储活动的开始时间,b[] 存储活动的结束时间
int begini, endi = 0; // begini 临时存储活动的开始时间,endi 记录当前已安排活动的最晚结束时间
int c = 0; // c 记录最多可以安排的活动数量
// 三、数据输入
cin >> n; // 输入活动数量
for(int i = 0; i < n; i++) {
cin >> a[i] >> b[i]; // 输入每个活动的开始时间和结束时间
}
// 四、数据处理 - 按结束时间排序活动
// 冒泡排序算法,保证b[](结束时间数组)升序排列,同时同步调整a[](开始时间数组)
for(int i = 0; i < n - 1; i++) {
for(int j = 0; j < n - 1 - i; j++) {
if(b[j] >= b[j+1]) { // 发现逆序则交换
swap(b[j], b[j+1]); // 交换结束时间
swap(a[j], a[j+1]); // 同步交换开始时间,保持活动信息对应
}
}
}
// 五、根据排序后的活动选择不冲突的活动
for(int i = 0; i < n; i++) {
if(a[i] >= endi) { // 当前活动的开始时间大于等于上一个活动的结束时间,说明不冲突
endi = b[i]; // 更新最晚结束时间为当前活动的结束时间
++c; // 可以安排此活动,活动数量加一
}
}
// 六、输出结果
cout << c << endl; // 输出最多能安排的活动数量
return 0; // 程序正常结束
}
思路二:
#include<bits/stdc++.h>
using namespace std;
// 全局变量定义
int n; // 活动数量
int a[110], b[110]; // a[i] 表示活动i的开始时间,b[i] 表示活动i的结束时间
bool c[110]; // 标记活动是否已被选择,默认全为false
int myleft = INT_MIN, myright = INT_MAX; // 初始化活动的最左(最早开始)和最右(最晚结束)时间
// 函数:寻找最早结束且未被选择的活动的结束时间
int myFindLeft(){
int min_index, m_min = INT_MAX;
for(int i = 0; i < n; i++){
if(m_min > b[i] && !c[i] && a[i] >= myleft){ // 寻找符合条件的活动
m_min = b[i];
min_index = i;
}
}
if(b[min_index] <= myright){ // 确保找到的活动在时间窗口内
c[min_index] = true; // 标记活动为已选择
return b[min_index];
}else{
return 0; // 未找到符合条件的活动
}
}
// 函数:寻找最晚开始且未被选择的活动的开始时间
int myFindRight(){
int max_index, m_max = INT_MIN;
for(int i = 0; i < n; i++){
if(m_max < a[i] && !c[i] && b[i] <= myright){ // 寻找符合条件的活动
m_max = a[i];
max_index = i;
}
}
if(a[max_index] >= myleft){ // 确保找到的活动在时间窗口内
c[max_index] = true; // 标记活动为已选择
return a[max_index];
}else{
return 0; // 未找到符合条件的活动
}
}
int main(){
// 问题分析与数据定义同上...
// 数据输入
cin >> n;
for(int i = 0; i < n; i++){
cin >> a[i] >> b[i];
}
// 数据计算
int count = 0, newLeft, newRight;
// 主循环,尝试交替选择左右边界内的活动
while(true){
newLeft = myFindLeft(); // 寻找左侧(最早结束)活动
newRight = myFindRight(); // 寻找右侧(最晚开始)活动
// 如果两边都没有找到新的活动,则退出循环
if(newLeft == 0 && newRight == 0) break;
// 根据找到的活动更新边界并计数
if(newLeft > myleft){
myleft = newLeft;
++count;
}
if(newRight < myright && newRight != 0){
myright = newRight;
++count;
}
}
// 输出结果
cout << count;
return 0;
}
问题:1456. 淘淘捡西瓜
类型:贪心
题目描述:
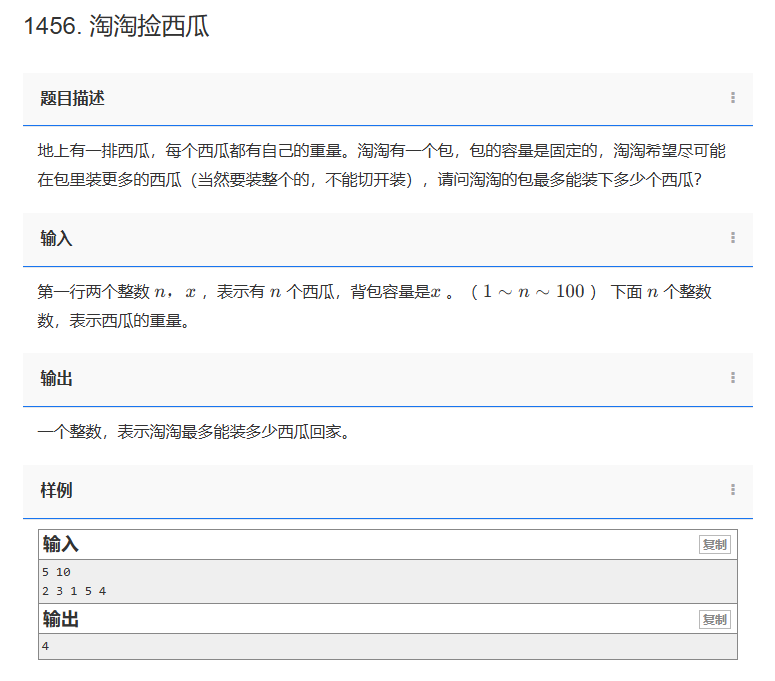
地上有一排西瓜,每个西瓜都有自己的重量。淘淘有一个包,包的容量是固定的,淘淘希望尽可能在包里装更多的西瓜(当然要装整个的,不能切开装),请问淘淘的包最多能装下多少个西瓜?
输入:
第一行两个整数n,x ,表示有 n 个西瓜,背包容量是x 。( 1∼n∼100 ) 下面 n 个整数,表示西瓜的重量。
输出:
一个整数,表示淘淘最多能装多少西瓜回家。
样例:
输入:
5 10
2 3 1 5 4
输出:
4
1.分析问题
- 已知:n 个西瓜,背包容量是x。
- 未知:表示淘淘最多能装多少西瓜回家。
- 关系:贪心。
2.定义变量
- 定义了整型变量n(西瓜总数)、x(背包容量)、整型数组a[110](存放每个西瓜的重量)和整型变量c(计数器,表示能装入的西瓜数量)。
//二、数据定义
int n,x,a[110],c=0;
3.输入数据
- 读取西瓜总数n和背包容量x,随后读取每个西瓜的重量。
//三、数据输入
cin>>n>>x;
for(int i=0;i<n;i++){
cin>>a[i];
}
4.数据计算
- 首先使用sort(a, a+n)对西瓜重量进行升序排序。
- 接着,遍历排序后的西瓜数组,对于每个西瓜,如果其重量加上当前背包已有的物品重量不超过总容量x,就将该西瓜装入背包(减去西瓜重量x -= a[i]),并累加西瓜计数c++。
- 如果某西瓜无法装入(即x-a[i]<0),则直接跳出循环,因为后面的西瓜更重,也不可能装入。
//四、数据计算
sort(a,a+n);
for(int i = 0; i < n; i++) {
// 如果当前西瓜重量加上已装西瓜总重量不超过背包容量
if(x - a[i] >= 0) {
x -= a[i]; // 减去当前西瓜的重量,模拟装入背包
++c; // 成功装入一个西瓜,计数加一
} else {
// 若当前西瓜不能装入,直接终止循环,因为后面的西瓜更重,也无法装入
break;
}
}
5.输出结果
- 输出能装入背包的最大西瓜数量c。
//五、输出结果
cout<<c;
return 0;
完整代码如下:
#include<bits/stdc++.h>
using namespace std;
int main(){
// 一、问题分析
// 面临问题:有n个西瓜,每个西瓜有不同的重量,需要将这些西瓜放入一个容量为x的背包中。
// 目标:确定在不超过背包容量的前提下,淘淘最多能携带多少个西瓜回家。
// 方法:采用贪心策略,优先选择重量轻的西瓜装入背包。
// 二、数据定义
int n, x; // n: 西瓜总数, x: 背包容量
int a[110]; // a[]: 存储每个西瓜的重量
int c = 0; // c: 记录能装入背包的西瓜数量
// 三、数据输入
cin >> n >> x; // 输入西瓜总数和背包容量
for(int i = 0; i < n; i++) {
cin >> a[i]; // 输入每个西瓜的重量
}
// 四、数据处理 - 贪心策略选择西瓜
// 首先对西瓜重量进行升序排序,确保先考虑轻的西瓜
sort(a, a + n);
// 遍历排序后的西瓜数组
for(int i = 0; i < n; i++) {
// 如果当前西瓜重量加上已装西瓜总重量不超过背包容量
if(x - a[i] >= 0) {
x -= a[i]; // 减去当前西瓜的重量,模拟装入背包
++c; // 成功装入一个西瓜,计数加一
} else {
// 若当前西瓜不能装入,直接终止循环,因为后面的西瓜更重,也无法装入
break;
}
}
// 五、输出结果
cout << c; // 输出能装入背包的西瓜数量
return 0; // 程序正常结束
}
问题:1485. 接水问题
类型:贪心
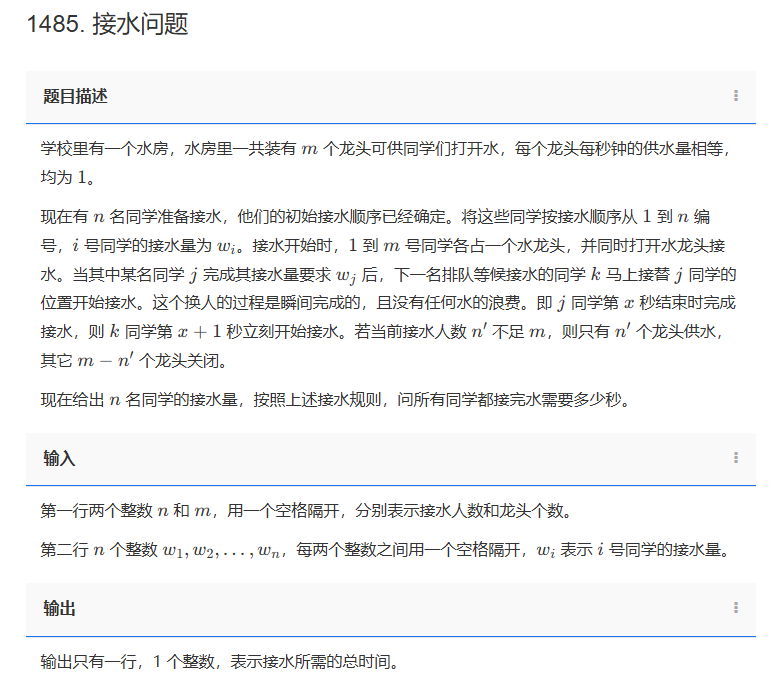
题目描述:
学校里有一个水房,水房里一共装有 m 个龙头可供同学们打开水,每个龙头每秒钟的供水量相等,均为 1。
现在有 n 名同学准备接水,他们的初始接水顺序已经确定。将这些同学按接水顺序从 1 到 n 编号,i 号同学的接水量为 wi。接水开始时,1 到 m 号同学各占一个水龙头,并同时打开水龙头接水。当其中某名同学 j 完成其接水量要求 wj 后,下一名排队等候接水的同学 k 马上接替 j 同学的位置开始接水。这个换人的过程是瞬间完成的,且没有任何水的浪费。即 j 同学第 x 秒结束时完成接水,则 k 同学第 x+1 秒立刻开始接水。若当前接水人数 n 不足 m,则只有 n个龙头供水,其它 m−n 个龙头关闭。
现在给出 n 名同学的接水量,按照上述接水规则,问所有同学都接完水需要多少秒。
输入:
第一行两个整数 n 和 m,用一个空格隔开,分别表示接水人数和龙头个数。
第二行 n 个整数 w1,w2,…,wn,每两个整数之间用一个空格隔开,wi 表示 i 号同学的接水量。
输出:
输出只有一行,1 个整数,表示接水所需的总时间。
样例1:
输入:
5 3
4 4 1 2 1
输出:
4
样例2:
输入:
8 4
23 71 87 32 70 93 80 76
输出:
163
1.分析问题
- 已知:接水人数n和龙头个数m,同学的接水量x;
- 未知:所有同学都接完水需要多少秒ma。
- 关系:贪心。
2.定义变量
- a: 每个水龙头打水的时间 n: 学生人数, m: 水龙头数量, mi: 最小累积量的水龙头索引, ma: 最大累积时间, x: 当前学生的接水量。
//二、数据定义
int n,m,a[110]={},mi,ma,x;
3.输入数据
- 输入学生人数和水龙头数量。
- 输入每个学生的接水时间 。
- 将接水时间累加到当前最小的水龙头上,越小的水龙排队时间越小 。
//三、数据输入
cin>>n>>m;
for(int i=0;i<n;i++){
cin>>x;
mi=1;
for(int j=2;j<=m;j++){
if(a[j]<a[mi]){
mi=j;
}
}
a[mi]+=x;
}
4.数据计算
- 找出所有水龙头中的最大的接水时间,如果该水龙头接水完毕,其他也完毕 。
//四、数据计算
ma=a[1];
for(int i=2;i<=m;i++){
if(a[i]>ma) ma=a[i];
}
5.输出结果
- 输出接水的最短时间。
//五、输出结果
cout<<ma;
完整代码如下:
#include<bits/stdc++.h>
using namespace std;
int main(){
//一、分析问题
//已知:接水人数n和龙头个数m,同学的接水量x;
//未知:所有同学都接完水需要多少秒。
//关系:贪心。
//二、数据定义
int n,m,a[110]={},mi,ma,x; // a: 每个水龙头打水的时间 n: 学生人数, m: 水龙头数量, mi: 最小累积量的水龙头索引, ma: 最大累积时间, x: 当前学生的接水量
//三、数据输入
cin>>n>>m; // 输入学生人数和水龙头数量
for(int i=0;i<n;i++){
cin>>x;// 输入每个学生的接水时间
mi=1;
for(int j=2;j<=m;j++){
if(a[j]<a[mi]){
mi=j;
}
}
a[mi]+=x;// 将接水时间累加到当前最小的水龙头上,越小的水龙排队时间越小
}
//四、数据计算
ma=a[1];
for(int i=2;i<=m;i++){
if(a[i]>ma) ma=a[i];// 找出所有水龙头中的最大的接水时间,如果该水龙头接水完毕,其他也完毕
}
//五、输出结果
cout<<ma; // 输出接水的最短时间
return 0;
}
三、感谢
如若本文对您的学习或工作有所启发和帮助,恳请您给予宝贵的支持——轻轻一点,为文章点赞;若觉得内容值得分享给更多朋友,欢迎转发扩散;若认为此篇内容具有长期参考价值,敬请收藏以便随时查阅。
每一次您的点赞、分享与收藏,都是对我持续创作和分享的热情鼓励,也是推动我不断提供更多高质量内容的动力源泉。期待我们在下一篇文章中再次相遇,共同攀登知识的高峰!