概述

从课程地图上可以看出来，这是本门课程中第一次正式的介绍强化学习的算法，并且是一个 model-based 的算法，而在下一节课将会介绍第一个 model-free 的算法（在 chapter 5）。而这两节和之前所学的 BOE 是密切相关的：value iteration 在 BOE 中已经介绍过，但是不够正式，而 policy iteration 则是下一节 Monte Carlo Learning 的一个基础。

本节课大纲如下：

这三者联系同样非常紧密，实际上值迭代和策略迭代是 truncated policy iteration 的两种极端情况。

Value iteration algorithm

从上图可以看到，实际上之前通过迭代的方式求解贝尔曼最优公式的过程就是这里要学习的 value iteration 算法。

其算法过程包括两部分，第一部分就是首先会给定 Vk，要求解这个嵌套在这个 BOE 式子当中的一个优化问题也就是求解 Π，当这个 Π 被求解出来以后，然后再求解出来这个 Vk+1 即可。

也就是下图所对应的两个步骤：

注意上图中最后留下的问题：Vk 是一个 state value 吗？

乍一看好像 Vk 就是一个 state value，然而并不是。右边是 Vk，左边是V(k+1)，如果左边是 Vk 那么该式子确实是一个贝尔曼公式，求得的解就是 state value，但是左边并不是 Vk，因此并非 state value。
那它是什么呢？其实就是一个向量，一个值，Vk 只是某次迭代过程中还没有收敛的一个值。为什么叫值迭代算法？就是因为它可以是任意的值，然后慢慢迭代到 state value 罢了。

接下来我们使用 elementwise form 来实现 值迭代 算法（矩阵向量形式适合理论研究）：

首先是第一步，策略更新：

然后是第二步，值更新：

合起来的过程如下：

算法实例：

Policy iteration algorithm

这样一个过程可以被下图表示出来：

接下来回答上面 PPT 中的问题：

对于求解 state value 有两种方法，我们这里会介绍常用的迭代的方式。

接下来是实现 policy iteration 的做法：

伪代码如下：

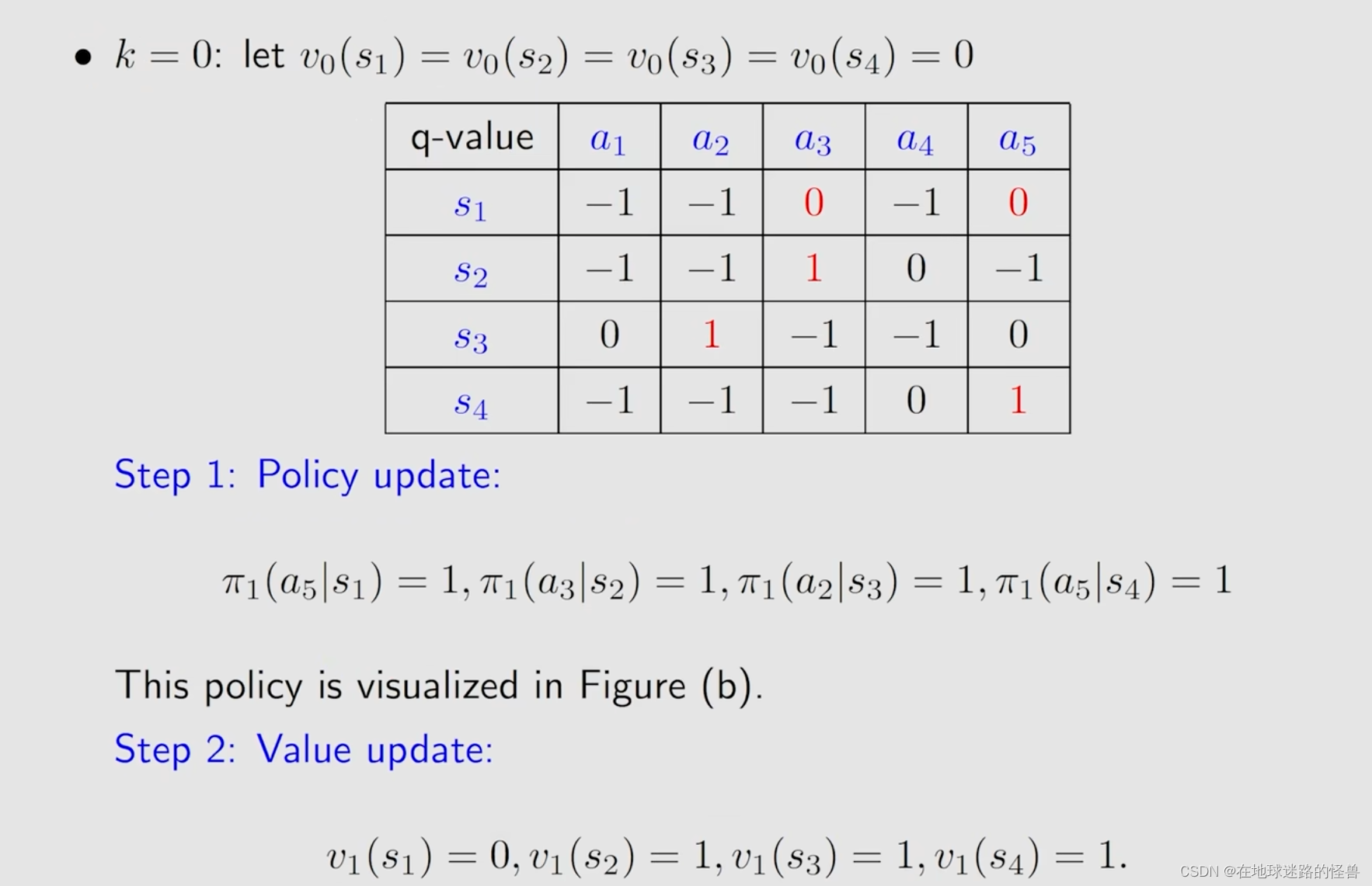
一个简单的例子用来加深印象：

这是一个比较简单的例子，因此迭代次数较少。

Truncated policy iteration algorithm

首先比较一下上文说的 value iteration 和 policy iteration：

从上图可以看出，二者其实是非常类似的：

但还是会有区别的：

上图是一个典型的求解贝尔曼公式id一个迭代算法，但是马上就有新的东西要出现了：

为什么叫 truncated 呢？从上图容易知道，就是因为从 j 出发到后边无穷的这些步全都没有了，全部都截断了，因此 truncated policy iteration 显然是 value iteration 和 policy iteration 更一般化的形式。

还有一个需要强调的点是，policy iteration 这个算法其只在理论上存在，在实际当中是不可能存在的，因为它需要计算无穷多步，在实际当中是不可能计算无穷多步的。

我们经常做的实际上就是判断比如说 VΠ1(j) 和 VΠ1(j-1) 这两个直接的误差是不是已经足够小了，如果足够小那么就可以停止迭代了，而这显然是有限步的操作。

因此实际上我们平常所做的 policy iteration 其实就是 truncated policy iteration。

其伪代码思路如下：

然而上图有一个明显的问题就是其没有计算无穷多步，因此计算出来的 Vk 实际上并不是 VΠk，那么这种截断会不会带来一些问题呢？

不会的：

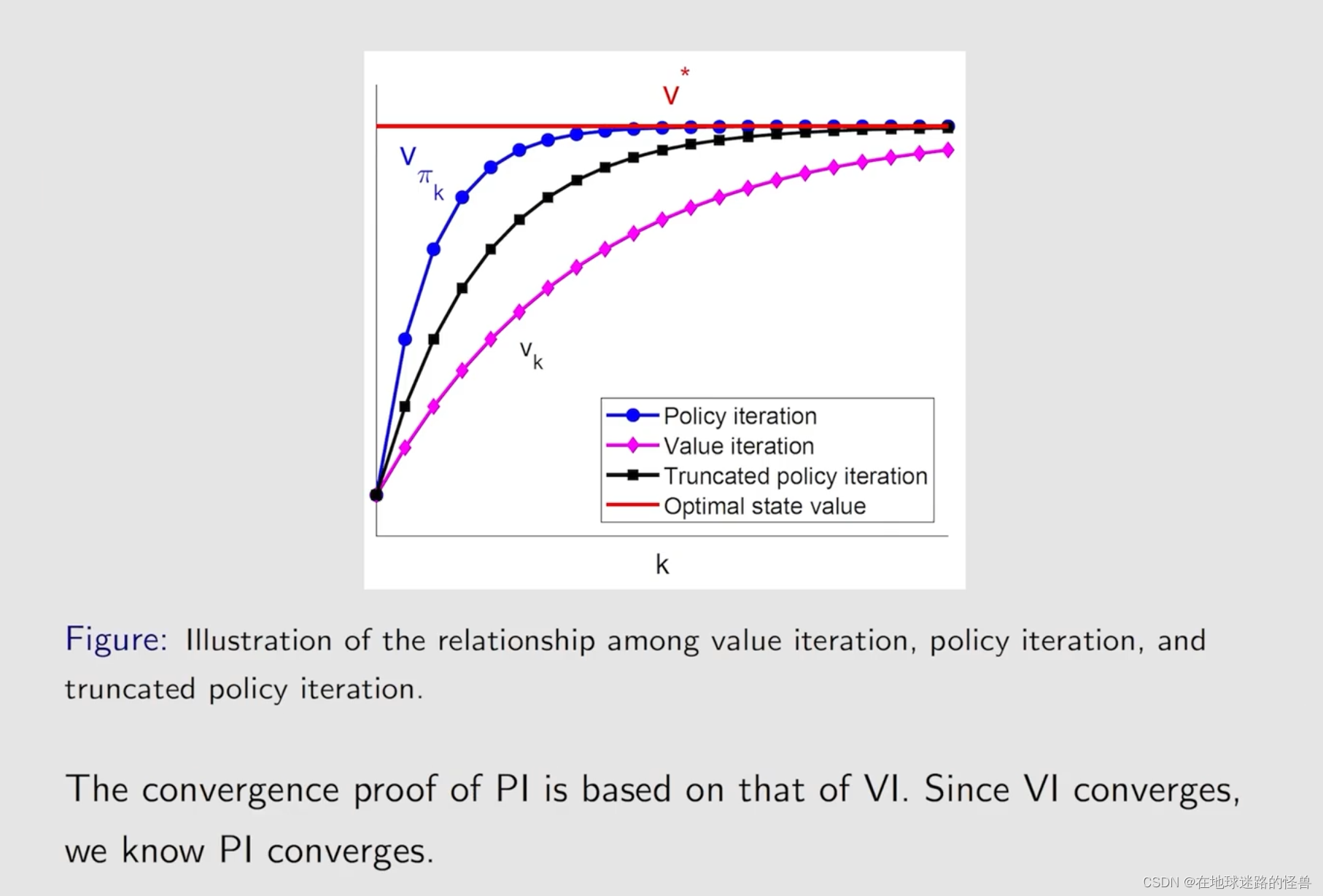
上面的结果可以通过下面的图示更好的展示：

Summary