并联机器人轨迹规划原理

轨迹规划：并联机器人的轨迹规划相比于串联机器人更加严苛，因为在大多数工作场合都有高速、高精度、轻载的特征。其一般运动轨迹为 Point-To-Point，对这始末两点的轨迹规划在 Delta 机器人乃至所有机器人领域具有重要的意义，这直接影响机器人的工作节拍、动态性能、运动控制。

对于每一段轨迹，末端执行器抓起和放下经历：静止启动—高速运行—减速停止这一过程。为了避免对机器太大的冲击，保证运动的平稳性，末端的初始和终止时刻的速度、加速度应都为零，这样轨迹函数关于时间的一阶和二阶导数必然是连续的，能够避免机器人启动和停止时的冲击，对设备造成损坏。因此，对于轨迹函数中的时间、 (角)位移、速度、加速度有如下要求：

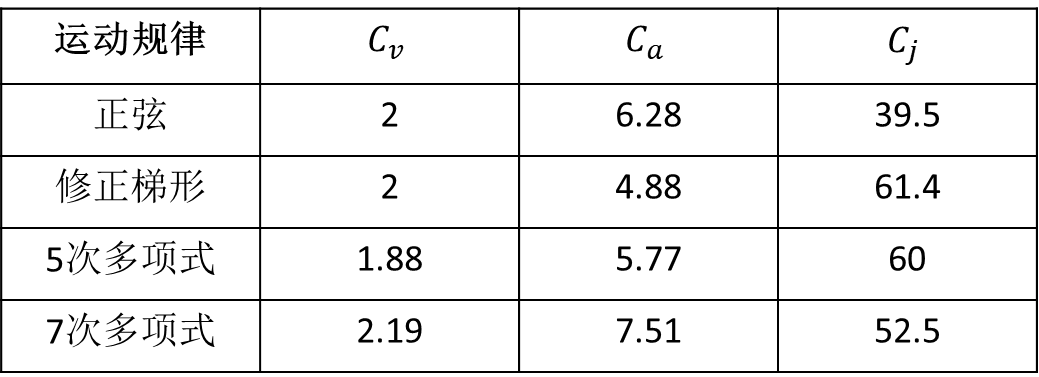
其中T为完成单周期任务的时间，S为完成单周期(角)位移，满足此函数要求的运动规律有很多。 速度的最大值𝑉_𝑚𝑎𝑥 、加速度的最大值𝑎_𝑚𝑎𝑥以及跃度最大值𝑗_𝑚𝑎𝑥，其表达式为：

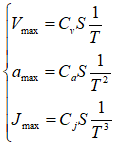
clear all
clc

ti=0:0.01:5;

T=5;

th=sA(0.100,0.02,0.730)


amax1=5.77*th(1,1)*pi/(180*T^2);
amax2=5.77*th(1,2)*pi/(180*T^2);
amax3=5.77*th(1,3)*pi/(180*T^2);


skd1j=[];
skdd1j=[];

skd2j=[];
skdd2j=[];

skd3j=[];
skdd3j=[];
for i=1:size(ti,2)
    
    t=ti(1,i)
    
    sk1=(amax1*(T^2)/5.77)*(6*(t/T)^5-15*(t/T)^4+10*(t/T)^3); 
    skd1=(2*amax1*T/5.77)*(30*(t/T)^4-60*(t/T)^3+30*(t/T)^2); 
    skdd1=(amax1/5.77)*(120*(t/T)^3-180*(t/T)^2+60*(t/T)); 
    
    sk2=(amax2*(T^2)/5.77)*(6*(t/T)^5-15*(t/T)^4+10*(t/T)^3); 
    skd2=(2*amax2*T/5.77)*(30*(t/T)^4-60*(t/T)^3+30*(t/T)^2); 
    skdd2=(amax2/5.77)*(120*(t/T)^3-180*(t/T)^2+60*(t/T)); 
    
    sk3=(amax3*(T^2)/5.77)*(6*(t/T)^5-15*(t/T)^4+10*(t/T)^3); 
    skd3=(2*amax3*T/5.77)*(30*(t/T)^4-60*(t/T)^3+30*(t/T)^2); 
    skdd3=(amax3/5.77)*(120*(t/T)^3-180*(t/T)^2+60*(t/T)); 
    
    skd1j=[skd1j skd1];
    skdd1j=[skdd1j abs(skdd1)];
    
    skd2j=[skd2j skd2];
    skdd2j=[skdd2j abs(skdd2)];
    
    skd3j=[skd3j skd3];
    skdd3j=[skdd3j abs(skdd3)];
    
end

figure(1);
plot(ti,-skd1j);
hold on 
plot(ti,-skd2j);
hold on 
plot(ti,-skd3j);
title('速度曲线');
legend('theta1d','theta2d','theta3d');

figure(2);
plot(ti,skdd1j);
hold on 
plot(ti,skdd2j);
hold on 
plot(ti,skdd3j);
title('加速度曲线');
legend('theta1dd','theta2dd','theta3dd');



% sA(0,0,0.5453210063806)
% sk=6*(t/5)^5-15*(t/5)^4+10*(t/5)^3;

往期推荐