LeetCode 算法：路径总和 III c++

news2024/11/19 13:23:20

原题链接🔗：路径总和 III
难度：中等⭐️⭐️

题目

给定一个二叉树的根节点 root ，和一个整数 targetSum ，求该二叉树里节点值之和等于 targetSum 的路径的数目。

路径不需要从根节点开始，也不需要在叶子节点结束，但是路径方向必须是向下的（只能从父节点到子节点）。

示例 1：
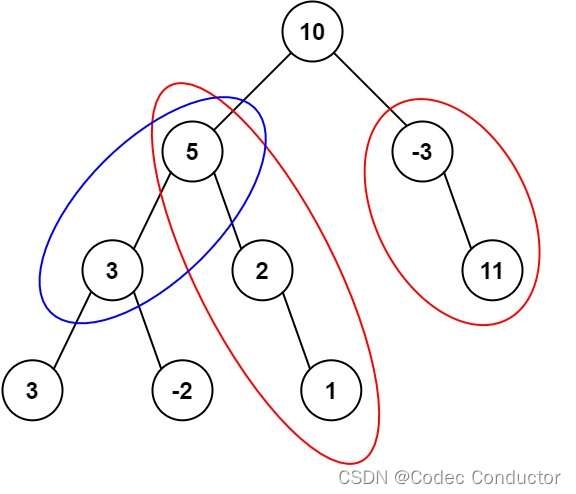
在这里插入图片描述

输入：root = [10,5,-3,3,2,null,11,3,-2,null,1], targetSum = 8
输出：3
解释：和等于 8 的路径有 3 条，如图所示。

示例 2：

输入：root = [5,4,8,11,null,13,4,7,2,null,null,5,1], targetSum = 22
输出：3

提示:

二叉树的节点个数的范围是 [0,1000]
-10⁹ <= Node.val <= 10⁹
-1000 <= targetSum <= 1000

题解

什么是深度优先搜索

深度优先搜索（Depth-First Search，简称 DFS）是一种用于遍历或搜索树或图的算法。这种算法会尽可能深地搜索树的分支，当节点 v 的所有可达的邻接节点都已被探索过，搜索回溯到发现节点 v 的那条边的起始节点，继续进行搜索。

深度优先搜索的基本思想是：

从起始节点开始：选择一个起始节点，将其标记为已访问。

访问邻接节点：从当前节点开始，选择一个未被访问的邻接节点，移动到该节点，并将该节点标记为已访问。

递归搜索：对新到达的节点，重复步骤2，直到找到一个没有未访问邻接节点的节点。

回溯：当当前节点的所有邻接节点都被访问过，或者没有更多的邻接节点时，回溯到前一个节点，继续搜索。

终止条件：当所有节点都被访问过，或者搜索完所有可能的路径时，搜索结束。

深度优先搜索可以用于多种场景，包括但不限于：

连通性问题：确定图中的节点是否全部连通。
拓扑排序：对有向无环图（DAG）的顶点进行排序。
路径查找：在图中查找从一个节点到另一个节点的路径。
解决数独：通过尝试不同的数字来解决数独问题。

深度优先搜索通常使用递归或显式的栈来实现。在树结构中，深度优先搜索可以确保每个节点只被访问一次，而在图中，为了避免重复访问节点，通常需要使用一个集合或数组来跟踪已访问的节点。

深度优先搜索的效率取决于图或树的结构，以及搜索的具体目标。在最坏的情况下，它可能需要检查所有可能的节点和边。

深度优先搜索法

解题思路：

LeetCode 上的 “路径总和 III” 可以通过深度优先搜索（DFS）来解决。以下是使用 DFS 解决这个问题的步骤：

定义递归函数：创建一个递归函数，该函数接收当前节点、当前路径和以及目标和。

初始化路径和：在递归函数中，更新当前路径和，即从根节点到当前节点的和。

检查当前节点：如果当前节点是叶子节点（即没有左右子节点），检查当前路径和是否等于目标和。如果是，增加路径计数。

递归遍历子树：对当前节点的左右子节点进行递归调用，更新路径和并传递给子树。

回溯：在递归调用结束后，需要回溯以撤销当前节点的选择，这通常通过减少当前路径和来实现。

路径计数：在递归过程中，除了检查当前路径和是否等于目标和外，还需要将当前路径和与目标和做差，然后检查差值是否存在于一个哈希表中，这个哈希表用于存储从根到当前节点的路径和。

使用哈希表优化：在递归过程中，如果当前节点的路径和减去目标和的结果存在于哈希表中，那么从当前节点到叶子节点的路径中，存在一条路径的和等于目标和。

返回结果：在递归的底部，返回路径计数。

复杂度：时间复杂度O(N²)，空间复杂度O(N)。
c++ demo：

#include <iostream>
#include <unordered_map>

using namespace std;

// 定义二叉树的节点结构
struct TreeNode {
    int val;
    TreeNode* left;
    TreeNode* right;
    TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
};

class Solution {
public:
    int rootSum(TreeNode* root, int targetSum) {
        if (!root) {
            return 0;
        }

        int ret = 0;

        if (root->val == targetSum) {
            ret++;
        }

        ret += rootSum(root->left, targetSum - root->val);
        ret += rootSum(root->right, targetSum - root->val);

        return ret;
    }

    int pathSum(TreeNode* root, int targetSum) {
        if (!root) {
            return 0;
        }

        int ret = rootSum(root, targetSum);
        ret += pathSum(root->left, targetSum);
        ret += pathSum(root->right, targetSum);
        return ret;
    }
};


int main() {
    // 构建一个简单的二叉树
    TreeNode* root = new TreeNode(10);
    root->left = new TreeNode(5);
    root->right = new TreeNode(-3);
    root->left->left = new TreeNode(3);
    root->left->right = new TreeNode(2);
    root->right->right = new TreeNode(11);
    root->left->right->right = new TreeNode(1);
    root->left->left->left= new TreeNode(3);
    root->left->left->right = new TreeNode(-2);

    // 创建 Solution 对象
    Solution solution;
    int result = solution.pathSum(root, 8); // 寻找路径和为8的路径数量

    cout << "Number of paths with sum 8: " << result << endl;

    // 释放二叉树占用的内存
    delete root->left->left->right;
    delete root->left->left->left;
    delete root->left->right->right;
    delete root->left->left;
    delete root->left->right;
    delete root->right->right;
    delete root->left;
    delete root->right;
    delete root;

    return 0;
}