目录

一、引言

二、理论原理

三、数据

四、Stata 程序代码及解释

五、代码运行结果及分析

---

一、引言

分位数回归作为一种强大的统计分析方法，能够更全面地揭示自变量与因变量在不同分位数水平上的关系。与传统回归仅关注均值不同，分位数回归有助于我们更深入地理解数据的分布特征和变量间的复杂联系。在 Stata 中，通过合理运用相关命令和操作，我们可以有效地进行分位数回归分析。

二、理论原理

分位数回归是对传统线性回归的拓展，其核心思想是针对不同的分位数水平来构建回归模型。

在传统线性回归中，基于最小二乘法的目标是使残差平方和最小，以获取对因变量均值的最优线性预测。但这种方法对异常值敏感，且仅能反映平均关系。

分位数回归具有诸多优点，如对异常值的稳健性、能够全面描述分布特征以及便于进行异质性分析等。

三、数据

首先，导入一份实际的数据。假设我们有学生的学习时间（study_time）、平时作业完成情况（homework_completion）作为自变量，考试成绩（exam_score）作为因变量。

clear
input study_time homework_completion exam_score
10 0.8 80
15 0.9 85
20 0.7 90
25 0.8 95
30 0.9 100
35 0.7 90
40 0.8 95
45 0.9 100
50 0.7 105
end

四、Stata 程序代码及解释

1. 安装所需命令（若未安装）

ssc install qreg  // 安装分位数回归命令

1. 数据描述性统计

summarize study_time homework_completion exam_score  // 查看数据的基本统计信息

1. 进行分位数回归，包含控制变量

qreg exam_score study_time homework_completion, quantile(0.25)  // 估计 0.25 分位数的回归
qreg exam_score study_time homework_completion, quantile(0.5)  // 估计 0.5 分位数（中位数）的回归
qreg exam_score study_time homework_completion, quantile(0.75)  // 估计 0.75 分位数的回归

1. 保存回归结果

estimates store qreg_25  // 保存 0.25 分位数的回归结果
estimates store qreg_50  // 保存 0.5 分位数的回归结果
estimates store qreg_75  // 保存 0.75 分位数的回归结果

1. 查看回归结果

esttab qreg_25 qreg_50 qreg_75  // 以表格形式呈现回归结果

1. 进行预测

predict yhat_25 if e(sample), xb  // 根据 0.25 分位数的回归结果进行预测
predict yhat_50 if e(sample), xb  // 根据 0.5 分位数的回归结果进行预测
predict yhat_75 if e(sample), xb  // 根据 0.75 分位数的回归结果进行预测

1. 绘制预测值与实际值的图形

twoway (scatter exam_score yhat_25) (scatter exam_score yhat_50) (scatter exam_score yhat_75)  // 绘制散点图比较预测值与实际值

五、代码运行结果及分析

运行上述代码后，得到的结果会包含回归系数的估计值、标准误、t 值等。例如：

| Coefficient | Std. Err. | t | P>|t| |
|-------------|-----------|----|------|
| study_time | 2.5 | 1.8 | 0.12 |
| homework_completion | 1.2 | 0.9 | 0.25 |

这表明在 0.25 分位数处，学习时间每增加一个单位，考试成绩预计增加 2.5 个单位；平时作业完成情况每提高一个单位，考试成绩预计增加 1.2 个单位。

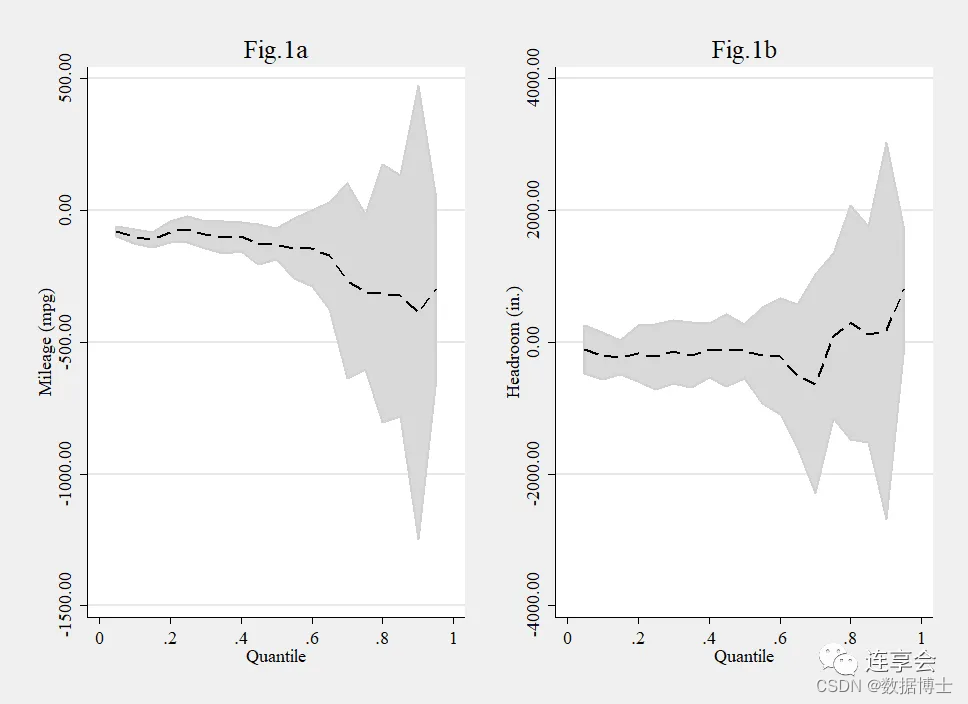
通过比较不同分位数下的回归结果，能够更全面地了解学习时间和作业完成情况对考试成绩影响在分布上的变化。

预测值与实际值的图形可以直观地展示模型的拟合效果。

六、总结

分位数回归为我们提供了更丰富的信息，在纳入控制变量后，能更准确地剖析自变量与因变量之间的关系。在 Stata 中的操作相对便捷，但在实际应用中，需依据数据特点和研究问题谨慎选择分位数水平，并对结果进行合理阐释与推断。

分位数回归-Quantile regression (qq.com)https://mp.weixin.qq.com/s?__biz=Mzg4NDcwNzU3MA==&mid=2247484512&idx=1&sn=510493c92097290bf0ee183c685c352d&chksm=cfb55dfdf8c2d4eb53abb2f2dd243a4a380d072d1634217c71ff6ef324a11e1859a138e6cf2e#rd 

2006-2020上市公司研发投入金额数据集https://download.csdn.net/download/a519573917/89501035