💓 博客主页:倔强的石头的CSDN主页
📝Gitee主页:倔强的石头的gitee主页
⏩ 文章专栏:《数据结构与算法》
期待您的关注
目录
一、引言
二、堆的基本概念
三、使用堆解决TopK问题
四、算法实现(C语言)
五、性能分析
一、引言
- TopK问题:在给定的一组数据或数据流中,找出最大的K个元素或最小的K个元素。
- 堆结构简介:堆是一种特殊的树形数据结构,每个父节点的值都大于(或小于)其子节点。这种性质使得堆在解决某些问题时非常高效。
- 堆结构在解决TopK问题中的优势:堆能够保持数据的有序性,同时插入和删除操作的时间复杂度较低,同时如果要查找的数据量较大时,将数据载入到内存中进行排序是不可能的,此时就离不开堆了,因此堆是解决TopK问题的理想选择。
二、堆的基本概念
关于堆的详细概念请参考前置文章
【数据结构与算法】探索数组在堆数据结构中的妙用:从原理到实现-CSDN博客
而本篇文章直接在堆的实现文件基础上解决TOPK问题
三、使用堆解决TopK问题
算法思想概述
如果数据较少,可以模仿堆排序(不需要进行完整的堆排序):
对数组建堆,然后堆顶数据与堆尾数据交换,重新调整,循环k次,数组的最后k个数就是要求得前k个最大(最小)的数
如果数据较大,没有办法将全部数据写入数组,就只能采用我们今天要介绍的算法了:
下面是重点,敲黑板!
分三步走
- 构建初始堆:从数据集中选择前K个元素并构建初始堆,求最大的k个元素建小堆,求最小的k个元素建大堆
- 处理数据流并维护堆:对于后续的数据,如果其大于(或小于)堆顶元素,则替换堆顶元素并重新调整堆;否则忽略该数据。 ——堆顶的数据相当于是一个准入门槛,是堆中的最小值。以求最大的k个元素为例,后续遍历的元素只有大于堆顶,才有机会入堆,并且因为堆顶是堆的最小值,不存在较大的数据挡在堆顶的情况
- 提取TopK元素:堆中的元素即为TopK元素,可以直接输出或进行后续处理。


四、算法实现(C语言)
这里以实现求前k各最大元素为例
之前已经写好的向下调整建小堆算法和交换函数:
void Swap(HPDataType* a, HPDataType* b)//交换函数
{
HPDataType tmp = *a;
*a = *b;
*b = tmp;
}
void Adjustdown(HPDataType* a, int parent, int n)//向下调整算法
{
assert(a);
int child = parent * 2 + 1;//先假设左孩子小
while (child < n)
{
if (child + 1 < n && a[child + 1] < a[child])//这里以小堆调整为例
child++;//如果右孩子存在,且右孩子小,父节点与右孩子进行比较
if (a[child] < a[parent])
{
Swap(&a[child], &a[parent]);
parent = child;
child = parent * 2 + 1;
}
else
break;
}
}造数据的过程以及TOPK问题的解决函数:
#if 1
//TOPK问题
void CreateNDate()// 造数据
{
int n = 1000;
srand(time(NULL));
const char* file = "data.txt";
FILE* fin = fopen(file, "w");//打开文件写数据
if (fin == NULL)
{
perror("fopen error");
return;
}
for (int i = 0; i < n; ++i)
{
int x = rand() % 1000000;//写入百万以内的随机数
fprintf(fin, "%d\n", x);
}
fclose(fin);
fin = NULL;
}
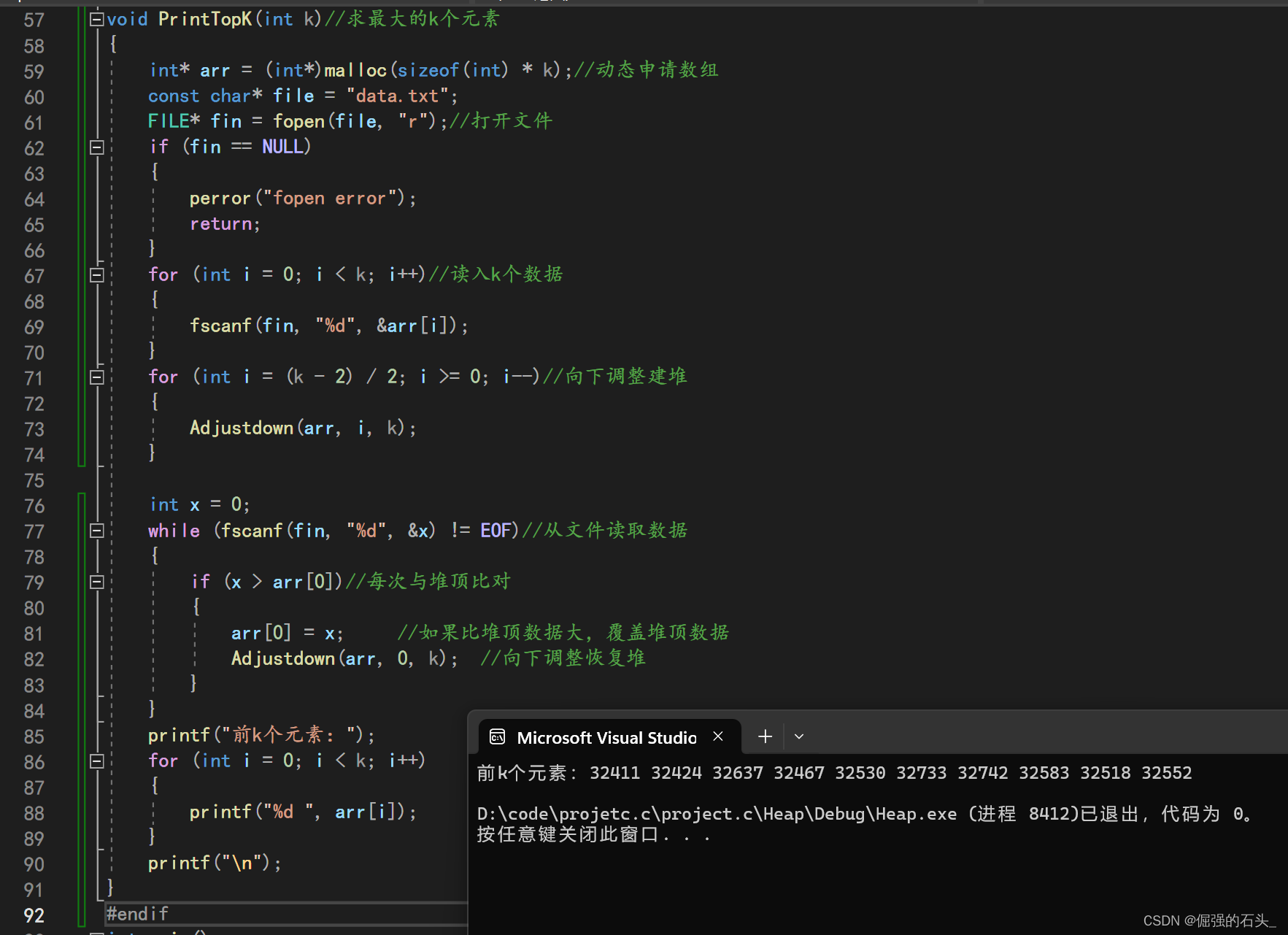
void PrintTopK(int k)//求最大的k个元素
{
int* arr = (int*)malloc(sizeof(int) * k);//动态申请数组
const char* file = "data.txt";
FILE* fin = fopen(file, "r");//打开文件
if (fin == NULL)
{
perror("fopen error");
return;
}
for (int i = 0; i < k; i++)//读入k个数据
{
fscanf(fin, "%d", &arr[i]);
}
for (int i = (k - 2) / 2; i >= 0; i--)//向下调整建堆
{
Adjustdown(arr, i, k);
}
int x = 0;
while (fscanf(fin, "%d", &x) != EOF)//从文件读取数据
{
if (x > arr[0])//每次与堆顶比对
{
arr[0] = x; //如果比堆顶数据大,覆盖堆顶数据
Adjustdown(arr, 0, k); //向下调整恢复堆
}
}
printf("前k个元素:");
for (int i = 0; i < k; i++)
{
printf("%d ", arr[i]);
}
printf("\n");
}
#endif
int main()
{
//test1();
//CreateNDate();
PrintTopK(10);
return 0;
} 
五、性能分析
- 时间复杂度:
- 当处理大数据集时,使用堆来解决TOPK问题可以显著提高性能。具体而言,如果我们使用最小堆来找出前K个最大的元素,或者最大堆来找出前K个最小的元素,时间复杂度可以大致控制在O(NlogK)内,其中N是数据集的大小。这是因为我们需要遍历整个数据集(O(N)),并且在每次插入或删除堆顶元素时,堆都需要进行调整(O(logK))。
- 相比之下,如果直接使用排序算法(如快速排序或归并排序),其时间复杂度通常为O(NlogN),这在N远大于K时,性能会显著下降。
- 空间复杂度:
- 使用堆解决TOPK问题只需要维护一个大小为K的堆,因此空间复杂度为O(K)。这意味着无论数据集的大小如何,我们只需要存储K个元素,这在处理大规模数据集时非常有效。
- 算法效率:
- 堆排序是一种原地排序算法(in-place sorting),即只需要使用O(1)的额外空间来进行排序。但是,在使用堆解决TOPK问题时,我们并不直接进行排序,而是利用堆的特性(最大堆或最小堆)来快速找出前K个最大或最小的元素。这种策略在处理TOPK问题时更加高效,因为我们只需要关心前K个元素,而不需要对整个数据集进行排序。
- 稳定性:
- 堆排序是一种不稳定的排序算法,因为在调整堆的过程中可能会改变相等元素的相对顺序。但是,在解决TOPK问题时,我们并不关心元素的相对顺序,只关心它们的大小关系。因此,堆的这种不稳定性对于解决TOPK问题并没有太大影响。
- 应用场景:
- 使用堆解决TOPK问题在多个领域都有广泛的应用,如搜索引擎、推荐系统、数据分析和数据挖掘等。在这些场景中,我们经常需要从大量数据中快速找出前K个最重要或最高排名的元素,堆排序的优势得以充分体现。