已知圆心坐标 (x0,y0),横轴 A(长半轴),竖轴 B(短半轴),角度 a,则圆边上点(x',y')的坐标为:
方法一 :

椭圆半径:
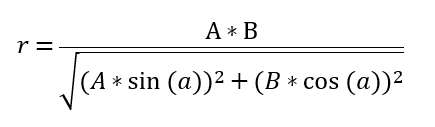
代码如下:
double A = 150; //横轴
double B = 100;//竖轴
double dCA = 30 * Math.PI / 180.0f; // 30度角,角度需要转换为弧度
double R = A * B / Math.Sqrt(Math.Pow(A * Math.Sin(dCA), 2) + Math.Pow(B * Math.Cos(dCA), 2)); //计算对应角度的半径
double x = x0 + R * Math.Cos(dCA);
double y = y0 + R * Math.Sin(dCA);方法二:
椭圆方程是:
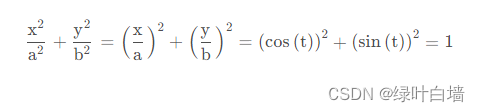
求离心角
如下图,已知椭圆的角p,要求主离心角t 。如下图,小圆为椭圆内切,大圆为椭圆外切。虚线除OE外,全为垂线
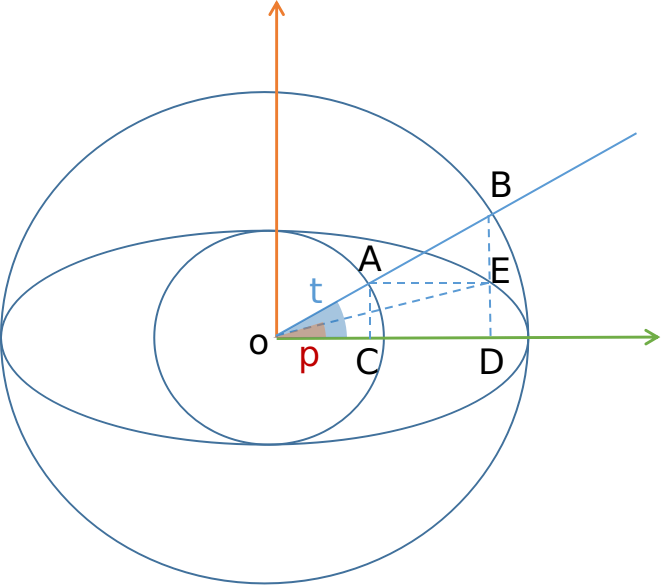
通过椭圆方程最终可以得到:
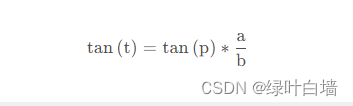
根据离心角求椭圆上给定角度的坐标
根据椭圆公式,可得
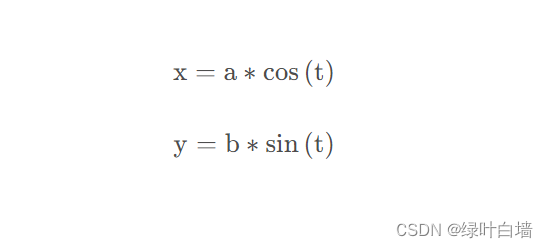
代码如下:
double A = 150; //横轴
double B = 100;//竖轴
double dCA = 30 * Math.PI / 180.0f; // 30度角, 角度需要转换为弧度
var ecc_angle = Math.Atan2(A * Math.Sin(dCA), B * Math.Cos(dCA));
var x = x0 + A * Math.Cos(ecc_angle);
var y = y0 + B * Math.Sin(ecc_angle);参考:
根据角度,求椭圆边上点的坐标_椭圆根据角度计算-CSDN博客
Qt绘图:求圆和椭圆上任意角度点的坐标_qdegreestoradians-CSDN博客