（内容源自详解MATLAB／SIMULINK 通信系统建模与仿真 刘学勇编著第三章内容，有兴趣的读者请阅读原书）
一、离散傅里叶变换
clear all
n=0:30;%信号的时间范围
x=sin(0.2*n).*exp(-0.1*n);
k=0:30;%频率范围
N=31;
Wnk=exp(-j*2*pi/N).^(n'*k);%DFT公式
X=x*Wnk;
subplot(2,1,1);stem(n,x);title('序列x');
subplot(2,1,2);stem(-15:15,[abs(X(17:end)) abs(X(1:16))]);%将DFT下标重新排列（DFT的默认下标为[0,N-1]）
title('X幅度');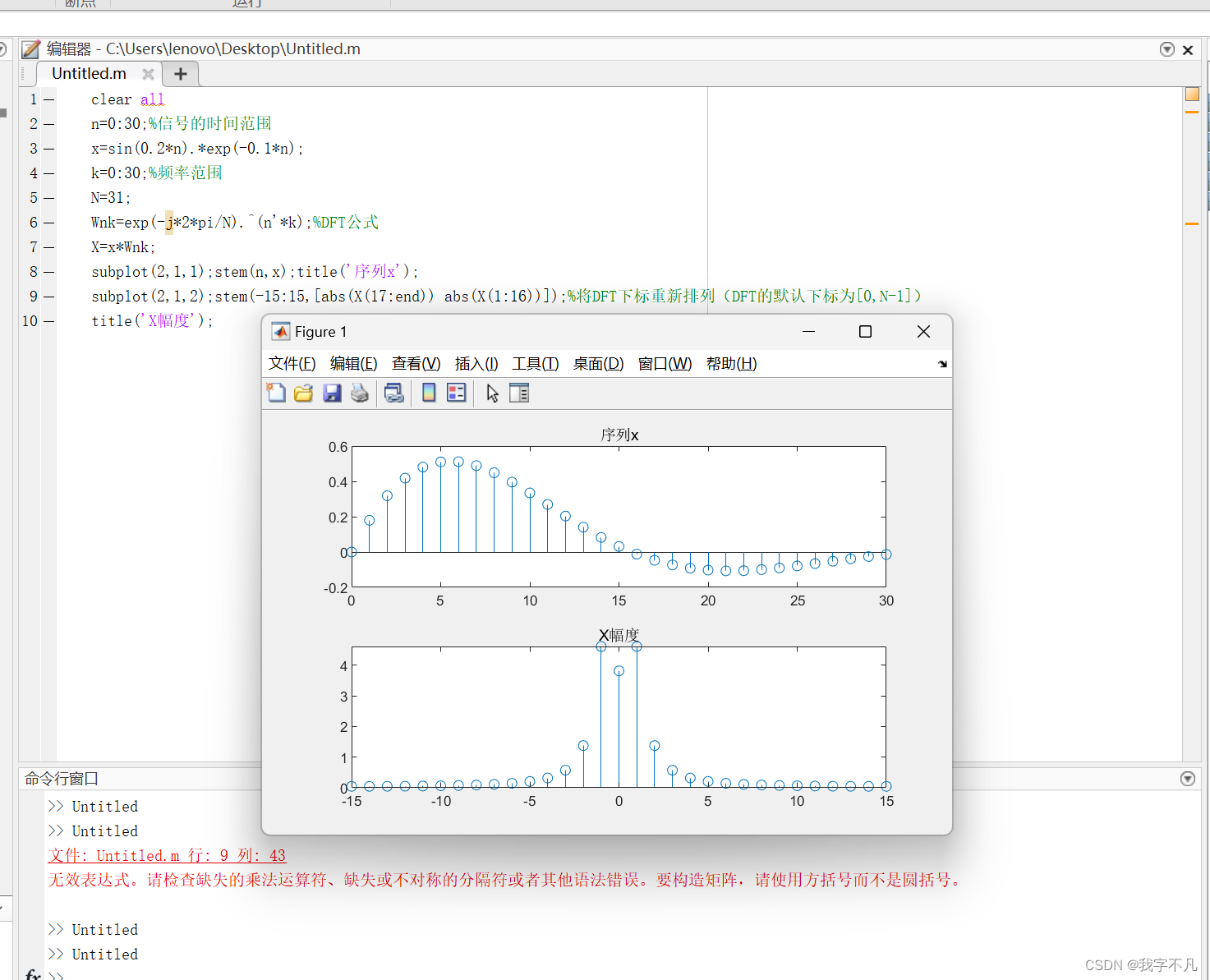
二、循环卷积
clear all
h=[6 3 4 2 1 -2];
x=[3 2 6 7 -1 -3];
h1=fliplr(h)%反转序列h
H=toeplitz(h,[h(1) h1(1:5)]);%生成循环矩阵
%T = toeplitz(c,r) 返回非对称托普利茨矩阵，
%其中 c 作为第一列，r 作为第一行。如果 c 和 r 的首个元素不同，toeplitz 将发出警告并使用列元素作为对角线
y=H*x';%计算循环卷积序列
H=fft(h);
X=fft(x);%两个序列的DFT
Y=H.*X;%循环卷积序列的DFT
y1=ifft(Y);%求循环卷积
subplot(2,1,1);stem(y);title('直接计算');
subplot(2,1,2);stem(y1);title('DFT计算'); 
这里用两种方得到的结果相同证明DFT运算内部是采用循环卷积而不是线性卷积
三、利用DFT求线性卷积
clear all
n1=0:20;
n2=0:10;
h=sinc(0.2*n1);
x=exp(-0.2*n2);
y=conv(x,h);%1.直接时域卷积
h1=[h zeros(1,length(x)-1)];
x1=[x zeros(1,length(h)-1)];%对x(n),h(n)进行扩展
H1=fft(h1);
X1=fft(x1);%计算DFT
Y1=H1.*X1;
y1=ifft(Y1);%2.利用IDFT算出时域卷积结果
subplot(2,1,1);stem(y);title('直接计算');
subplot(2,1,2);stem(y1);title('DFT计算'); 
虽然DFT内部采用的是循环卷积，但是我们可以利用DFT实现线性卷积结果的求解
四、Hilbert变换
clear all
ts=0.01;%这里是连续信号，所以需要对其进行采样才能处理，因为载波频率为20HZ，由采样定理至少需要40HZ，这里采用0.01s作为时间间隔
fs=1/ts;
t=0:ts:10;
df=fs/length(t);%DFT的频谱分辨率
f=-50:df:50-df;%生成频率矢量（用于画图）
x=exp(-10*abs(t-5)).*cos(2*pi*20*t);
X=fft(x)/fs;%求信号的频谱，因为原始信号是模拟信号，由抽样定理，必须求出FFT后再除以fs才是原模拟信号的频谱
xa=hilbert(x);%求解析信号
Xa=fft(xa)/fs;%求解析信号的频谱
subplot(2,1,1);plot(t,x);%利用时间分辨率画图
title('信号x');xlabel('时间t');
subplot(2,1,2);plot(f,fftshift(abs(X)));title('信号x幅度谱');xlabel('频率f');
%fftshift将0频分量移到中心，重新排列abs(X),由于X是复数，所以利用abs求包络
figure
subplot(2,1,1);plot(t,abs(xa));title('信号xa包络');xlabel('时间t');
subplot(2,1,2);plot(f,fftshift(abs(Xa)));title('信号xa幅度谱');xlabel('频率f');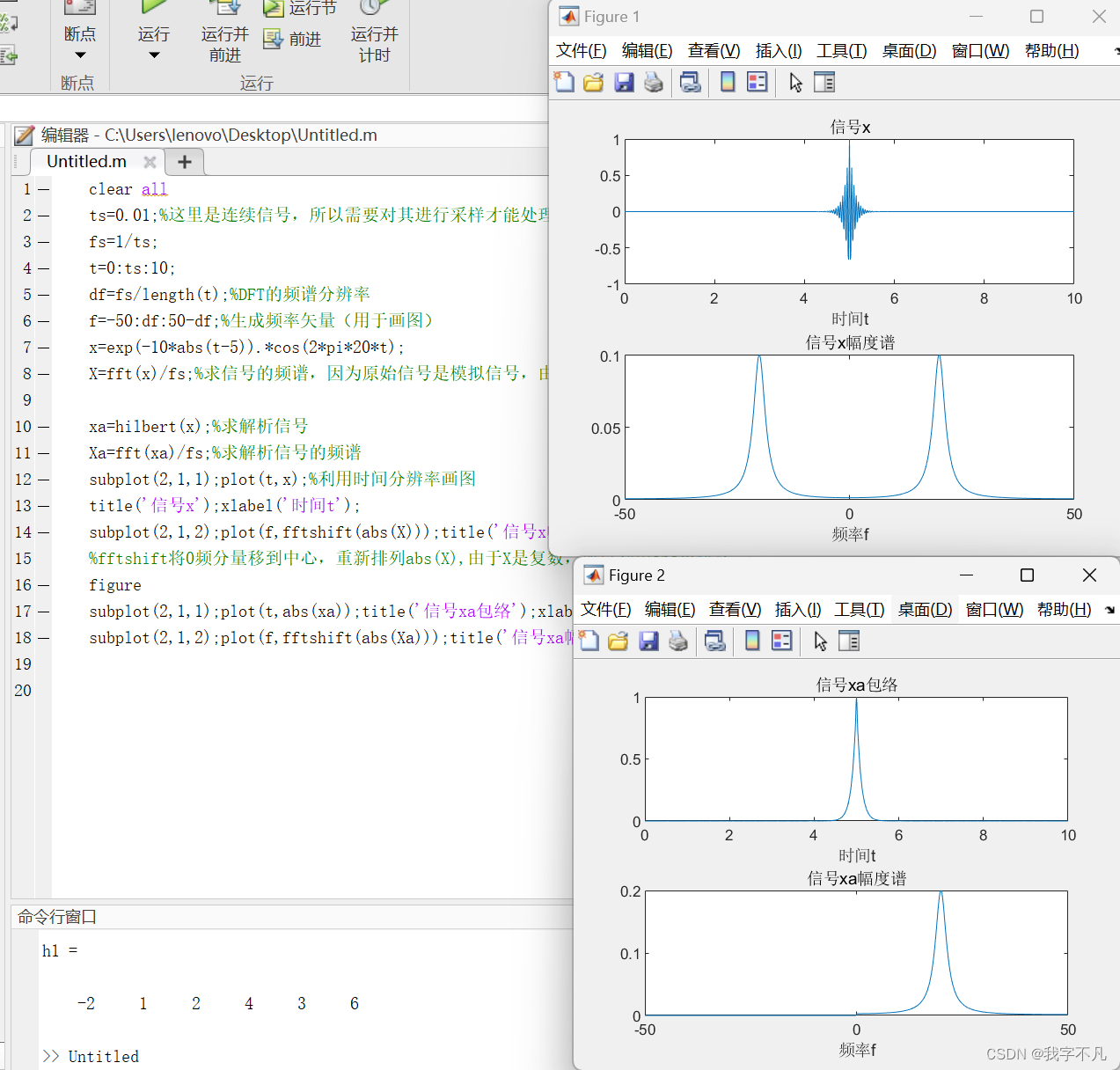
可以看到解析信号只包含正频率部分，且幅度值是原始信号频谱幅度值的两倍
五、带通信号的低通表示
clear all
ts=0.01;%这里是连续信号，所以需要对其进行采样才能处理，因为载波频率为20HZ，由采样定理至少需要40HZ，这里采用0.01s作为时间间隔
fs=1/ts;
t=0:ts:10;
df=fs/length(t);%DFT的频谱分辨率
f=-50:df:50-df;%生成频率矢量（用于画图）
x=exp(-10*abs(t-5)).*cos(2*pi*20*t);
X=fft(x)/fs;%求信号的频谱，因为原始信号是模拟信号，由抽样定理，必须求出FFT后再除以fs才是原模拟信号的频谱
xa=hilbert(x);%求解析信号
fc1=20;
x11=xa.*exp(-j*2*pi*fc1*t);%3-41公式，求20hz的低通信号
X11=fft(x11)/fs;%模拟信号，fft之后要除以fs
subplot(2,1,1);plot(t,real(x11));title('fc=20HZ时的低通信号同相分量');xlabel('时间t');
%同相分量就是解析信号中的实部
subplot(2,1,2);plot(f,fftshift(abs(X11)));title('fc=20HZ时的低通信号幅度谱');xlabel('频率f');
fc2=10;
x12=xa.*exp(-j*2*pi*fc2*t);
X12=fft(x12)/fs;
figure
subplot(2,1,1);plot(t,real(x12));title('fc=10HZ时的低通信号同相分量');xlabel('时间t');
subplot(2,1,2);plot(f,fftshift(abs(X12)));title('fc=10HZ时的低通信号幅度谱');xlabel('频率f');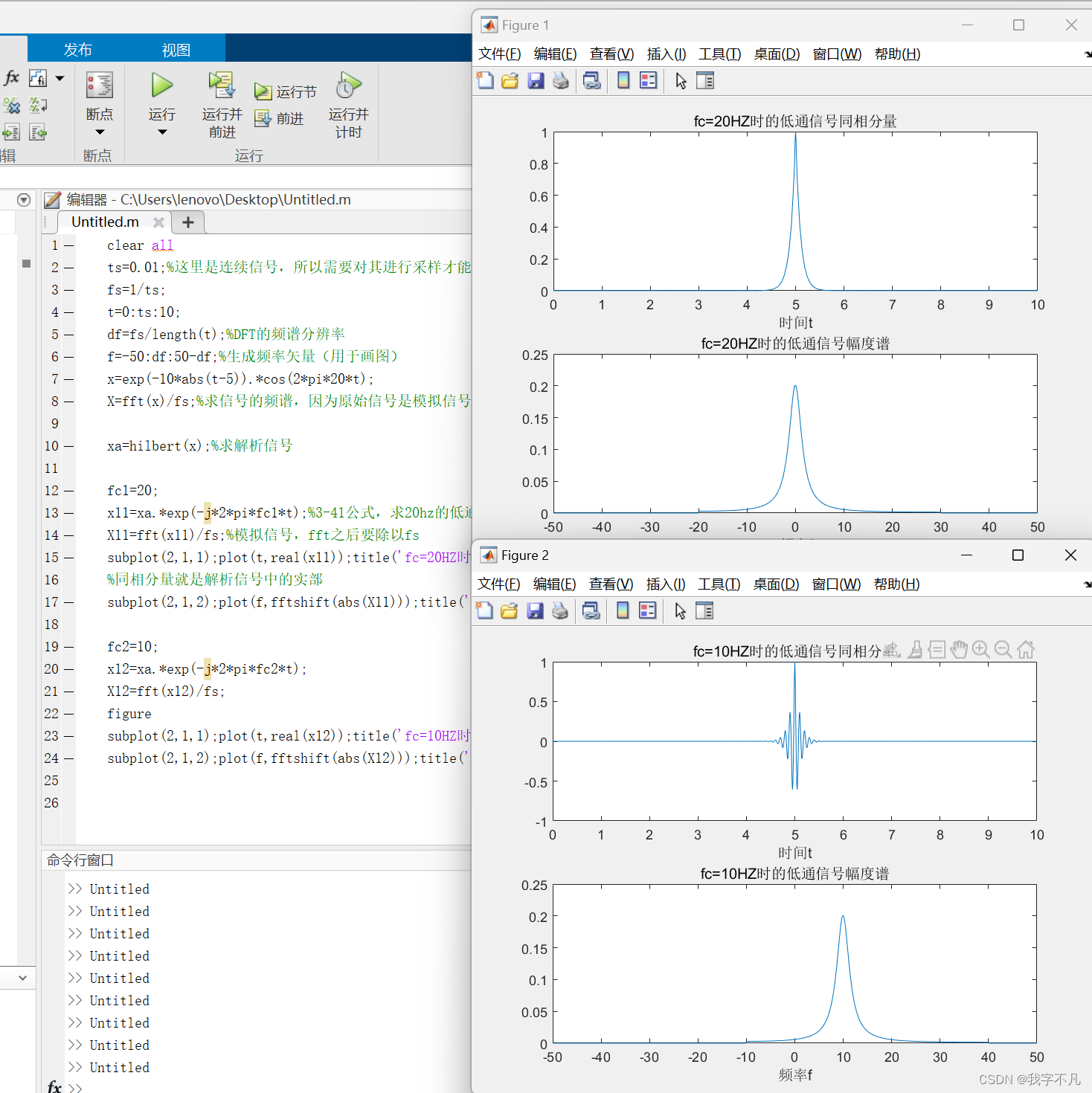
总结来说，就是利用解析信号和频移公式实现了带通信号的低通表示。
六、平稳随机过程
clear all
N1=2000;
N2=100;
x=randn(N2,N1);%产生一个100行，2000列的高斯分布随机数
for ii=1:N2%对每行进行循环
[Rx(ii,:),lags]=xcorr(x(ii,:),50,'coeff');%xcorr是用来计算自相关函数，第一个参数是自相关函数序列，
%第二个参数50是自相关值的最大时间偏移，lags就是[-50:50],可以理解为x中的每一行有2000个数，经过xcorr后每一行转化为101个数的
%自相关函数
Sf(ii,:)=fftshift(abs(fft(Rx(ii,:))));%功率谱密度是自相关函数的傅里叶变换
end
Rx_av=sum(Rx)/N2;%求100行的平均值
Sf_av=sum(Sf)/N2;
subplot(2,1,1);plot(lags,Rx_av);title('自相关函数')%画出在最大时间偏移上的自相关函数的变化情况
subplot(2,1,2);plot(lags,Sf_av);title('功率谱密度')
axis([-50 50 0 2]);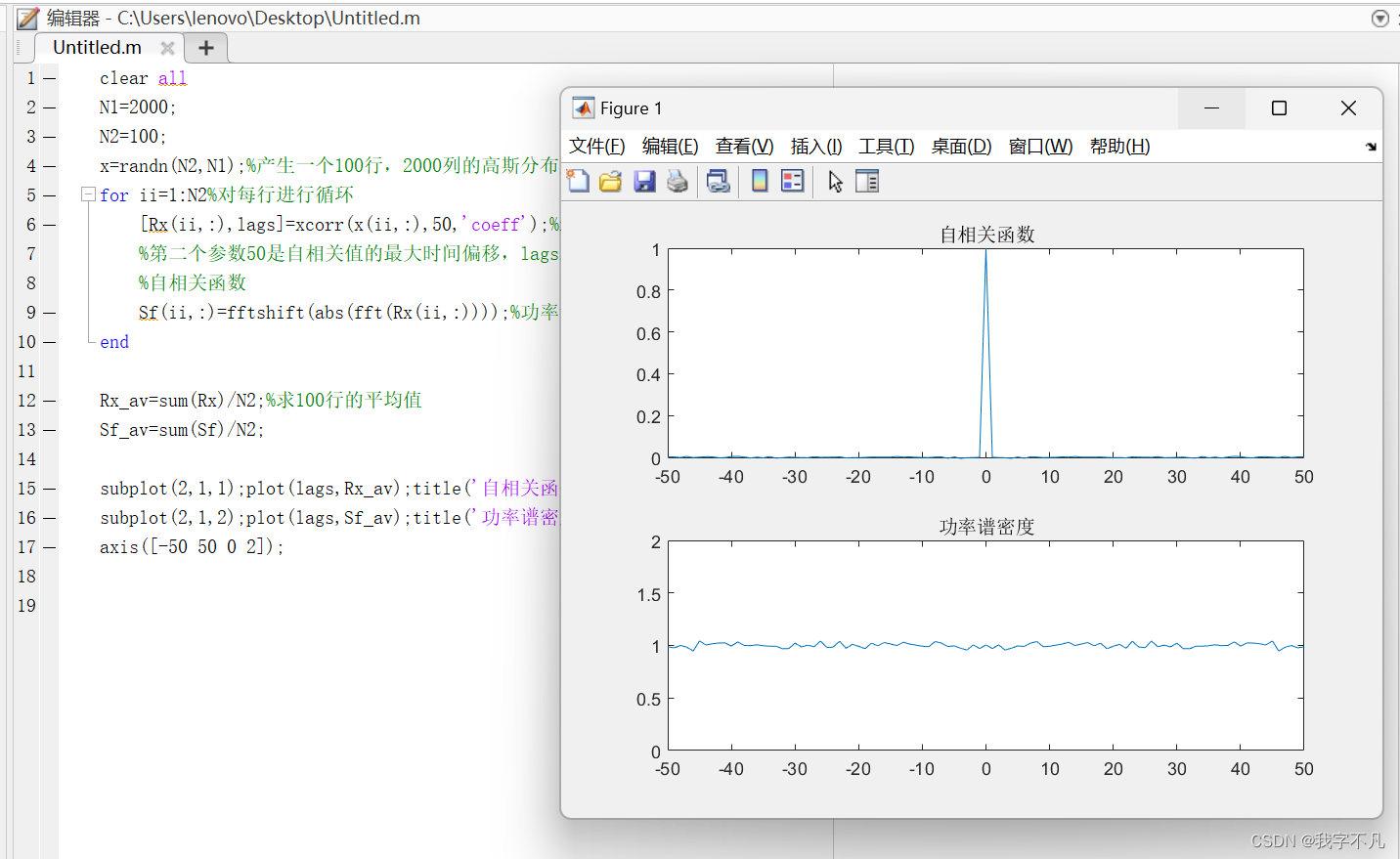 
七、带通随机过程
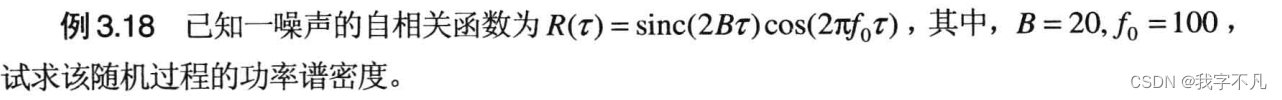
clear all
ts=0.002;
tao=-1:ts:1;%时间序列，因为自相关函数是连续函数，所以计算时需要抽样，因为函数是sinc形式，所以在【-1，1】之外值会很小
%可以忽略不计
B=20;
f0=100;
R=sinc(2*B*tao).*cos(2*pi*f0*tao);
fs=1/ts;
df=fs/length(tao);%频域分辨率，用采样频率/时间序列的长度
f=-fs/2:df:fs/2-df;
S=fft(R)/fs;%因为这里自相关函数是连续函数，所以求功率谱密度时还要在除以fs
%类似于之前的例子中模拟信号求fft之后还要再除以fs才是正确地结果
subplot(2,1,1);plot(tao,R);title('自相关函数');xlabel('tao');ylabel('R');
subplot(2,1,2);plot(f,fftshift(abs(S)));title('功率谱密度');xlabel('f');ylabel('S');
八、随机过程通过线性系统
clear all
N1=2000;
N2=100;
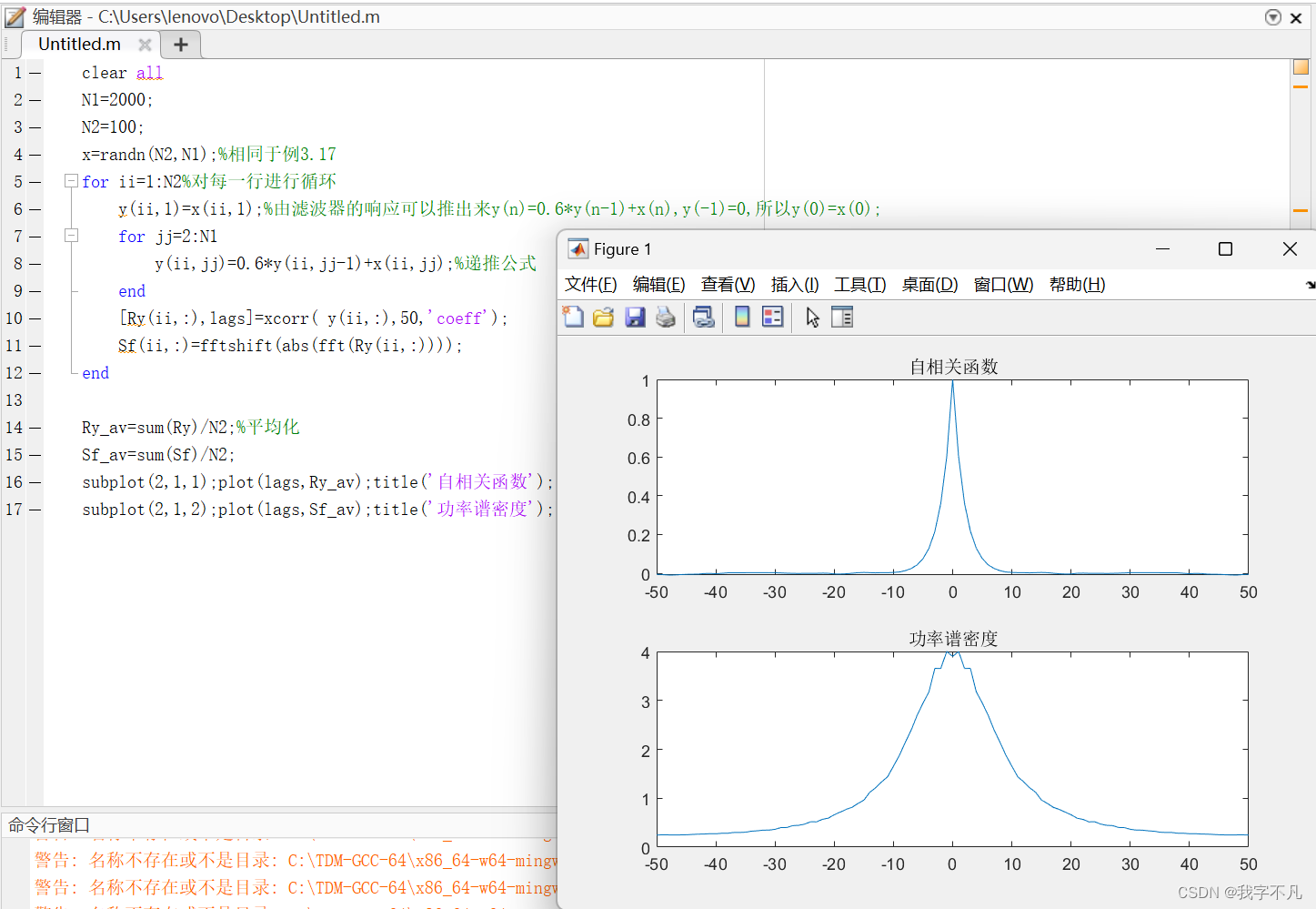
x=randn(N2,N1);%相同于例3.17
for ii=1:N2%对每一行进行循环
y(ii,1)=x(ii,1);%由滤波器的响应可以推出来y(n)=0.6*y(n-1)+x(n),y(-1)=0,所以y(0)=x(0);
for jj=2:N1
y(ii,jj)=0.6*y(ii,jj-1)+x(ii,jj);%递推公式
end
[Ry(ii,:),lags]=xcorr( y(ii,:),50,'coeff');
Sf(ii,:)=fftshift(abs(fft(Ry(ii,:))));
end
Ry_av=sum(Ry)/N2;%平均化
Sf_av=sum(Sf)/N2;
subplot(2,1,1);plot(lags,Ry_av);title('自相关函数');
subplot(2,1,2);plot(lags,Sf_av);title('功率谱密度');
