WGAN
E
x
∼
P
g
[
log
(
1
−
D
(
x
)
)
]
E
x
∼
P
g
[
−
log
D
(
x
)
]
\begin{aligned} & \mathbb{E}_{x \sim P_g}[\log (1-D(x))] \\ & \mathbb{E}_{x \sim P_g}[-\log D(x)] \end{aligned}
Ex∼Pg[log(1−D(x))]Ex∼Pg[−logD(x)]
原始 GAN 中判别器; 在 WGAN 两篇论文中称为 “the - log D alternative” 或 “the - log D trick”。WGAN 前作分别分析了这两种形式的原始 GAN 各自的问题所在 .
第一种原始 GAN 形式的问题
原始 GAN 中判别器要最小化如下损失函数,尽可能把真实样本分为正例,生成样本分为负例:
−
E
x
∼
P
r
[
log
D
(
x
)
]
−
E
x
∼
P
g
[
log
(
1
−
D
(
x
)
)
]
-\mathbb{E}_{x \sim P_r}[\log D(x)]-\mathbb{E}_{x \sim P_g}[\log (1-D(x))]
−Ex∼Pr[logD(x)]−Ex∼Pg[log(1−D(x))]
一句话概括:判别器越好,生成器梯度消失越严重。
在生成器 G 固定参数时最优的判别器 D 应该是什么,对于一个具体样本
x
x
x 它对公式 1 损失函数的贡献是
−
P
r
(
x
)
log
D
(
x
)
−
P
g
(
x
)
log
[
1
−
D
(
x
)
]
-P_r(x) \log D(x)-P_g(x) \log [1-D(x)]
−Pr(x)logD(x)−Pg(x)log[1−D(x)]
− P r ( x ) D ( x ) + P g ( x ) 1 − D ( x ) = 0 -\frac{P_r(x)}{D(x)}+\frac{P_g(x)}{1-D(x)}=0 −D(x)Pr(x)+1−D(x)Pg(x)=0
D ∗ ( x ) = P r ( x ) P r ( x ) + P g ( x ) D^*(x)=\frac{P_r(x)}{P_r(x)+P_g(x)} D∗(x)=Pr(x)+Pg(x)Pr(x)
如果 P r ( x ) = 0 P_r(x)=0 Pr(x)=0且 P g ( x ) ≠ 0 P_g(x)\neq0 Pg(x)=0 最优判别器就应该非常自信地给出概率 0;如果 P r ( x ) = P g ( x ) P_r(x)=P_g(x) Pr(x)=Pg(x)
说明该样本是真是假的可能性刚好一半一半,此时最优判别器也应该给出概率 0.5。
GAN 训练有一个 trick,就是别把判别器训练得太好,否则在实验中生成器会完全学不动(loss 降不下去),为了探究背后的原因,我们就可以看看在极端情况 —— 判别器最优时,生成器的损失函数变成什么。给公式 2 加上一个不依赖于生成器的项,使之变成
D
∗
(
x
)
D^*(x)
D∗(x) 带入 公式1 得到
E
x
∼
P
r
log
P
r
(
x
)
1
2
[
P
r
(
x
)
+
P
g
(
x
)
]
+
E
x
∼
P
g
log
P
g
(
x
)
1
2
[
P
r
(
x
)
+
P
g
(
x
)
]
−
2
log
2
\mathbb{E}_{x \sim P_r} \log \frac{P_r(x)}{\frac{1}{2}\left[P_r(x)+P_g(x)\right]}+\mathbb{E}_{x \sim P_g} \log \frac{P_g(x)}{\frac{1}{2}\left[P_r(x)+P_g(x)\right]}-2 \log 2
Ex∼Prlog21[Pr(x)+Pg(x)]Pr(x)+Ex∼Pglog21[Pr(x)+Pg(x)]Pg(x)−2log2
K L ( P 1 ∥ P 2 ) = E x ∼ P 1 log P 1 P 2 J S ( P 1 ∥ P 2 ) = 1 2 K L ( P 1 ∥ P 1 + P 2 2 ) + 1 2 K L ( P 2 ∥ P 1 + P 2 2 ) \begin{aligned} & K L\left(P_1 \| P_2\right)=\mathbb{E}_{x \sim P_1} \log \frac{P_1}{P_2} \\ & J S\left(P_1 \| P_2\right)=\frac{1}{2} K L\left(P_1 \| \frac{P_1+P_2}{2}\right)+\frac{1}{2} K L\left(P_2 \| \frac{P_1+P_2}{2}\right) \end{aligned} KL(P1∥P2)=Ex∼P1logP2P1JS(P1∥P2)=21KL(P1∥2P1+P2)+21KL(P2∥2P1+P2)
2 J S ( P r ∥ P g ) − 2 log 2 2 J S\left(P_r \| P_g\right)-2 \log 2 2JS(Pr∥Pg)−2log2
key point
在最优判别器下,我们可以把原始GAN定义的生成器loss等价变换为最小化真实分布 P r P_r Pr 与生成分布 P g P_g Pg 之间的JS散度。我们越训练判别器,它就越接近最优。 最小化生成器的 loss 也就会越近似于最小化$ P_r$ 和 P g P_g Pg 之间的JS 散度。
问题就出在这个 JS 散度上。我们会希望如果两个分布之间越接近它们的 JS 散度越小,我们通过优化 JS 散度就能将
P
g
P_g
Pg "拉向"
P
r
P_r
Pr, ,最终以假乱真。这个希望在两个分布有所重叠的时候是成立的,但是如果两个分布完全没有重叠的部分,或者它们重叠的部分可忽略(下面解释什么叫可忽略),它们的 JS 散度是多少呢? 答案是log2,因为对于任意一个 x 只有四种可能:
P
1
(
x
)
=
0
且
P
2
(
x
)
=
0
P
1
(
x
)
≠
0
且
P
2
(
x
)
≠
0
P
1
(
x
)
=
0
且
P
2
(
x
)
≠
0
P
1
(
x
)
≠
0
且
P
2
(
x
)
=
0
\begin{aligned} & P_1(x)=0 \text { 且 } P_2(x)=0 \\ & P_1(x) \neq 0 \text { 且 } P_2(x) \neq 0 \\ & P_1(x)=0 \text { 且 } P_2(x) \neq 0 \\ & P_1(x) \neq 0 \text { 且 } P_2(x)=0 \end{aligned}
P1(x)=0 且 P2(x)=0P1(x)=0 且 P2(x)=0P1(x)=0 且 P2(x)=0P1(x)=0 且 P2(x)=0
- 第一种对计算 JS 散度无贡献
- 第二种情况由于重叠部分可忽略所以贡献也为 0
- 第三种情况对公式 7 右边第一个项的贡献 log P 2 1 2 ( P 2 + 0 ) = log 2 \log \frac{P_2}{\frac{1}{2}\left(P_2+0\right)}=\log 2 log21(P2+0)P2=log2
- 第四种情况 J S ( P 1 ∥ P 2 ) = log 2 J S\left(P_1 \| P_2\right)=\log 2 JS(P1∥P2)=log2
即无论 P r P_r Pr 跟 P g P_g Pg 是远在天边,还是近在眼前,只要它们俩没有一点重叠或者重叠部分可忽略,JS 散度就固定是常数log2, 而这对于梯度下降方法意味着 —— 梯度为 0.此时对于最优判别器来说,生成器肯定是得不到一丁点梯度信息的;即使对于接近最优的判别器来说,生成器也有很大机会面临梯度消失的问题。
Manifold A topological space that locally resembles Euclidean space near each point when this Euclidean space is of dimension n n n ,the manifold is referred as manifold.
- 支撑集(support)其实就是函数的非零部分子集,比如 ReLU 函数的支撑集就是(0,+∞),一个概率分布的支撑集就是所有概率密度非零部分的集合。
- 流形(manifold)是高维空间中曲线、曲面概念的拓广,我们可以在低维上直观理解这个概念,比如我们说三维空间中的一个曲面是一个二维流形,因为它的本质维度(intrinsic dimension)只有 2,一个点在这个二维流形上移动只有两个方向的自由度。同理,三维空间或者二维空间中的一条曲线都是一个一维流形。
P r Pr Pr 已发现它们集中在较低维流形中。这实际上是流形学习的基本假设。想想现实世界的图像,一旦主题或所包含的对象固定,图像就有很多限制可以遵循,例如狗应该有两只耳朵和一条尾巴,摩天大楼应该有笔直而高大的身体,等等。这些限制使图像无法具有高维自由形式。
P g P_g Pg 也存在于低维流形中。每当生成器被要求提供更大的图像(例如 64x64),给定小尺寸(例如 100),噪声变量输入 z z z 这4096个像素的颜色分布是由100维的小随机数向量定义的,很难填满整个高维空间。
P r P_r Pr 和 P g P_g Pg 不重叠或重叠部分可忽略的可能性有多大?不严谨的答案是:非常大。
both P r P_r Pr and p g p_g pg 处于低维流形中,他们几乎不会相交。(wgan 前面一篇理论证明)
GAN 中的生成器一般是从某个低维(比如 100 维)的随机分布中采样出一个编码向量 z z z,再经过一个神经网络生成出一个高维样本(比如 64x64 的图片就有 4096 维)。当生成器的参数固定时,生成样本的概率分布虽然是定义在 4096 维的空间上,但它本身所有可能产生的变化已经被那个 100 维的随机分布限定了,其本质维度就是 100,再考虑到神经网络带来的映射降维,最终可能比 100 还小,所以生成样本分布的支撑集就在 4096 维空间中构成一个最多 100 维的低维流形,“撑不满” 整个高维空间。
在这里插入图片描述
我们就得到了 WGAN 前作中关于生成器梯度消失的第一个论证:在(近似)最优判别器下,最小化生成器的 loss 等价于最小化 P r P_r Pr 与 P g P_g Pg 之间的JS散度,而由于 P r P_r Pr 与 P g P_g Pg 几乎不可能有不可忽略的重叠,所以无论它们相距多远 JS 散度都是常数log2,最终导致生成器的梯度(近似)为 0,梯度消失。
原始 GAN 不稳定的原因就彻底清楚了:判别器训练得太好,生成器梯度消失,生成器 loss 降不下去;判别器训练得不好,生成器梯度不准,四处乱跑。只有判别器训练得不好不坏才行,但是这个火候又很难把握,甚至在同一轮训练的前后不同阶段这个火候都可能不一样,所以 GAN 才那么难训练。
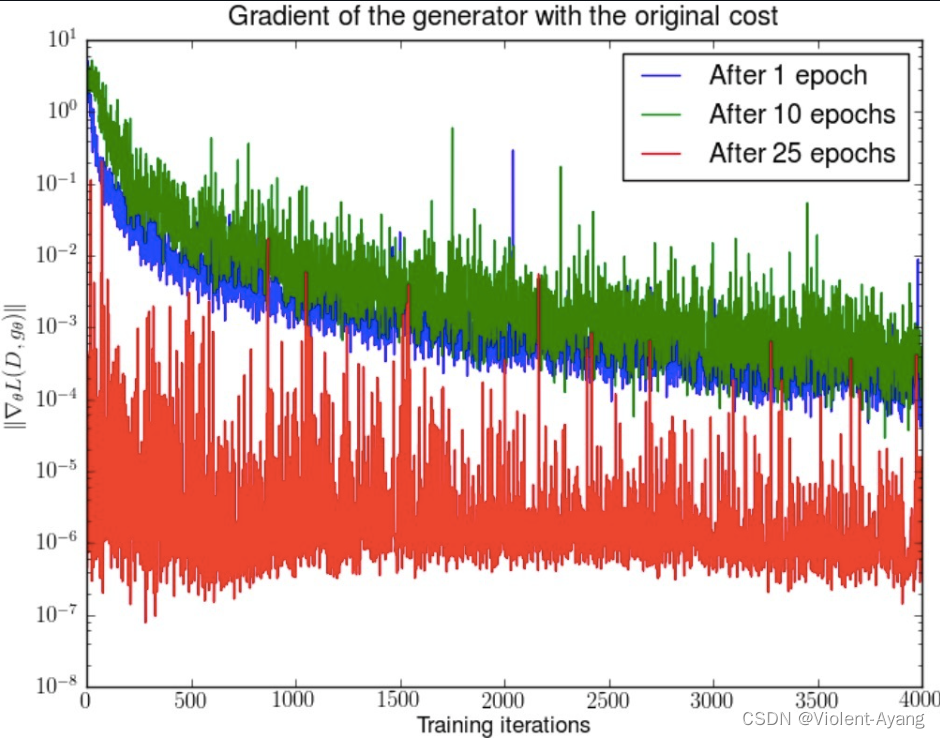
第二种原始 GAN 形式的问题 “the - log D trick”
一句话概括:最小化第二种生成器 loss 函数,会等价于最小化一个不合理的距离衡量,导致两个问题,一是梯度不稳定,二是 **Mode collapse 即多样性不足。**WGAN 前作又是从两个角度进行了论证
上文推导已经得到在最优判别器
D
∗
D^*
D∗ 下
E
x
∼
P
r
[
log
D
∗
(
x
)
]
+
E
x
∼
P
g
[
log
(
1
−
D
∗
(
x
)
)
]
=
2
J
S
(
P
r
∥
P
g
)
−
2
log
2
\mathbb{E}_{x \sim P_r}\left[\log D^*(x)\right]+\mathbb{E}_{x \sim P_g}\left[\log \left(1-D^*(x)\right)\right]=2 J S\left(P_r \| P_g\right)-2 \log 2
Ex∼Pr[logD∗(x)]+Ex∼Pg[log(1−D∗(x))]=2JS(Pr∥Pg)−2log2
K L ( P g ∥ P r ) = E x ∼ P g [ log P g ( x ) P r ( x ) ] = E x ∼ P g [ log P g ( x ) / ( P r ( x ) + P g ( x ) ) P r ( x ) / ( P r ( x ) + P g ( x ) ) ] = E x ∼ P g [ log 1 − D ∗ ( x ) D ∗ ( x ) ] = E x ∼ P g log [ 1 − D ∗ ( x ) ] − E x ∼ P g log D ∗ ( x ) \begin{aligned} K L\left(P_g \| P_r\right) & =\mathbb{E}_{x \sim P_g}\left[\log \frac{P_g(x)}{P_r(x)}\right] \\ & =\mathbb{E}_{x \sim P_g}\left[\log \frac{P_g(x) /\left(P_r(x)+P_g(x)\right)}{P_r(x) /\left(P_r(x)+P_g(x)\right)}\right] \\ & =\mathbb{E}_{x \sim P_g}\left[\log \frac{1-D^*(x)}{D^*(x)}\right] \\ & =\mathbb{E}_{x \sim P_g} \log \left[1-D^*(x)\right]-\mathbb{E}_{x \sim P_g} \log D^*(x) \end{aligned} KL(Pg∥Pr)=Ex∼Pg[logPr(x)Pg(x)]=Ex∼Pg[logPr(x)/(Pr(x)+Pg(x))Pg(x)/(Pr(x)+Pg(x))]=Ex∼Pg[logD∗(x)1−D∗(x)]=Ex∼Pglog[1−D∗(x)]−Ex∼PglogD∗(x)
E x ∼ P g [ − log D ∗ ( x ) ] = K L ( P g ∥ P r ) − E x ∼ P g log [ 1 − D ∗ ( x ) ] = K L ( P g ∥ P r ) − 2 J S ( P r ∥ P g ) + 2 log 2 + E x ∼ P r [ log D ∗ ( x ) ] \begin{aligned} \mathbb{E}_{x \sim P_g}\left[-\log D^*(x)\right] & =K L\left(P_g \| P_r\right)-\mathbb{E}_{x \sim P_g} \log \left[1-D^*(x)\right] \\ & =K L\left(P_g \| P_r\right)-2 J S\left(P_r \| P_g\right)+2 \log 2+\mathbb{E}_{x \sim P_r}\left[\log D^*(x)\right] \end{aligned} Ex∼Pg[−logD∗(x)]=KL(Pg∥Pr)−Ex∼Pglog[1−D∗(x)]=KL(Pg∥Pr)−2JS(Pr∥Pg)+2log2+Ex∼Pr[logD∗(x)]
注意上式最后两项不依赖于生成器 G G G ,最终得到最小化公式 3 等价于最小化 K L ( P g ∥ P r ) − 2 J S ( P r ∥ P g ) K L\left(P_g \| P_r\right)-2 J S\left(P_r \| P_g\right) KL(Pg∥Pr)−2JS(Pr∥Pg)
这个等价最小化目标存在两个严重的问题。第一是它同时要最小化生成分布与真实分布的 KL 散度,却又要最大化两者的 JS 散度,一个要拉近,一个却要推远!这在直观上非常荒谬,在数值上则会导致梯度不稳定,这是后面那个 JS 散度项的毛病。
第二,即便是前面那个正常的 KL 散度项也有毛病。因为 KL 散度不是一个对称的衡量 K L ( P g ∥ P r ) K L\left(P_g \| P_r\right) KL(Pg∥Pr) 与 K L ( P r ∥ P g ) K L\left(P_r \| P_g\right) KL(Pr∥Pg) 是有差别的。
Wasserstein 距离的优越性质
W ( P r , P g ) = inf γ ∼ Π ( P r , P g ) E ( x , y ) ∼ γ [ ∥ x − y ∥ ] W\left(P_r, P_g\right)=\inf _{\gamma \sim \Pi\left(P_r, P_g\right)} \mathbb{E}_{(x, y) \sim \gamma}[\|x-y\|] W(Pr,Pg)=γ∼Π(Pr,Pg)infE(x,y)∼γ[∥x−y∥]
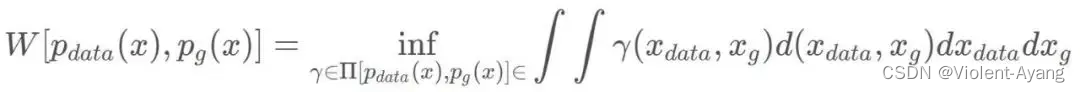
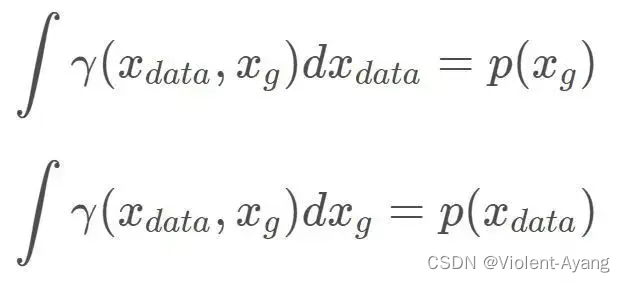

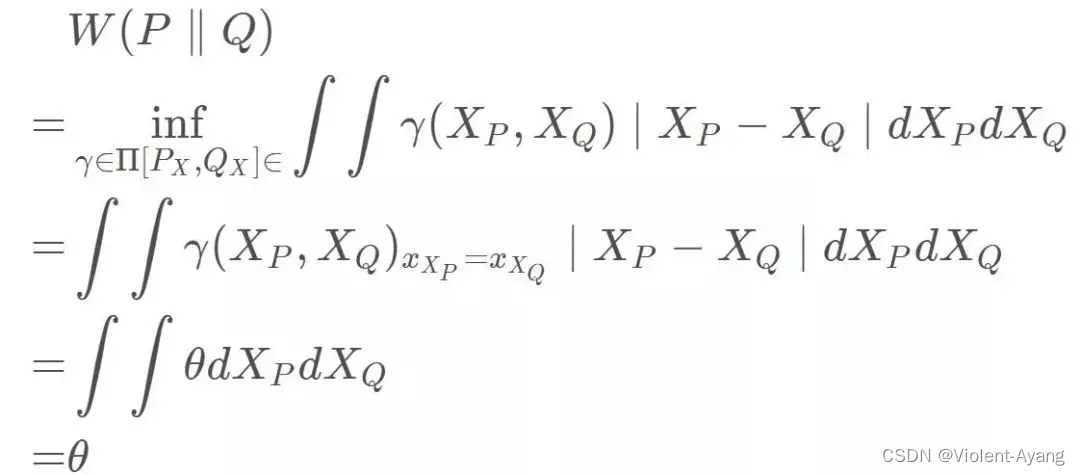
可以看出 Wasserstein 距离处处连续,而且几乎处处可导,数学性质非常好,能够在两个分布没有重叠部分的时候,依旧给出合理的距离度量。对于离散概率分布,Wasserstein 距离也被描述性地称为推土机距离 (EMD)。 如果我们将分布想象为一定量地球的不同堆,那么 EMD 就是将一个堆转换为另一堆所需的最小总工作量。
解释如下: Π ( P r , P g ) \Pi\left(P_r, P_g\right) Π(Pr,Pg) 是 P r P_r Pr 和 P g P_g Pg 组合起来的所有可能的联合分布的集合,反过来说, Π ( P r , P g ) \Pi\left(P_r, P_g\right) Π(Pr,Pg) 中每一个分布的边缘分布都是 P r P_r Pr 和 P g P_g Pg 。对于每一个可能的联合分布 γ \gamma γ 而言,可以从 中采样 ( x , y ) ∼ γ (x, y) \sim \gamma (x,y)∼γ 得到一个真实样本 x x x 和一个生成样本 y y y ,并算出这对样本的距离 ∥ x − y ∥ \|x-y\| ∥x−y∥ ,所 以可以计算该联合分布 γ \gamma γ 下样本对距离的期望值 E ( x , y ) ∼ γ [ ∥ x − y ∥ ] \mathbb{E}_{(x, y) \sim \gamma}[\|x-y\|] E(x,y)∼γ[∥x−y∥] 。在所有可能的联合分布中 够对这个期望值取到的下界inf in γ ∼ ( P r , P g ) E ( x , y ) ∼ γ [ ∥ x − y ∥ ] \operatorname{in}_{\gamma \sim\left(P_r, P_g\right)} \mathbb{E}_{(x, y) \sim \gamma}[\|x-y\|] inγ∼(Pr,Pg)E(x,y)∼γ[∥x−y∥] ,就定义为 Wasserstein 距离。
直观上可以把 E ( x , y ) ∼ γ [ ∥ x − y ∥ ] \mathbb{E}_{(x, y) \sim \gamma}[\|x-y\|] E(x,y)∼γ[∥x−y∥] 理解为在 γ \gamma γ 这个 “路径规划" 下把 P r P_r Pr 这堆 “沙土" 挪到 P g P_g Pg “位置” 所需的 “消耗”, 而 W ( P r , P g ) W\left(P_r, P_g\right) W(Pr,Pg) 就是 “最优路径规划" 下的 “最小消耗”,所以才 叫 Earth-Mover (推土机 ) 距离。
Wasserstein 距离相比 KL 散度、JS 散度的优越性在于,即便两个分布没有重叠,Wasserstein 距离仍然能够反映它们的远近。WGAN 本作通过简单的例子展示了这一点。考虑如下二维空间中 的两个分布 P 1 P_1 P1 和 P 2 , P 1 P_2 , P_1 P2,P1 在线段 A B \mathrm{AB} AB 上均匀分布, P 2 P_2 P2 在线段 C D \mathrm{CD} CD 上均匀分布,通过控制参数 θ \theta θ 可以控制着两个分布的距离远近。
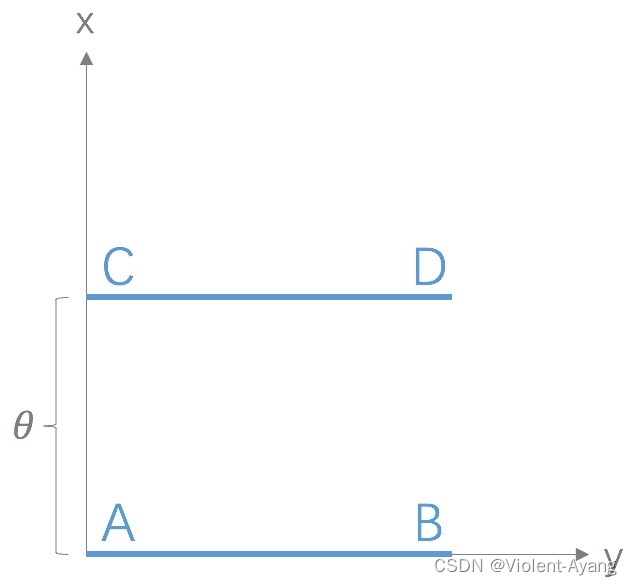
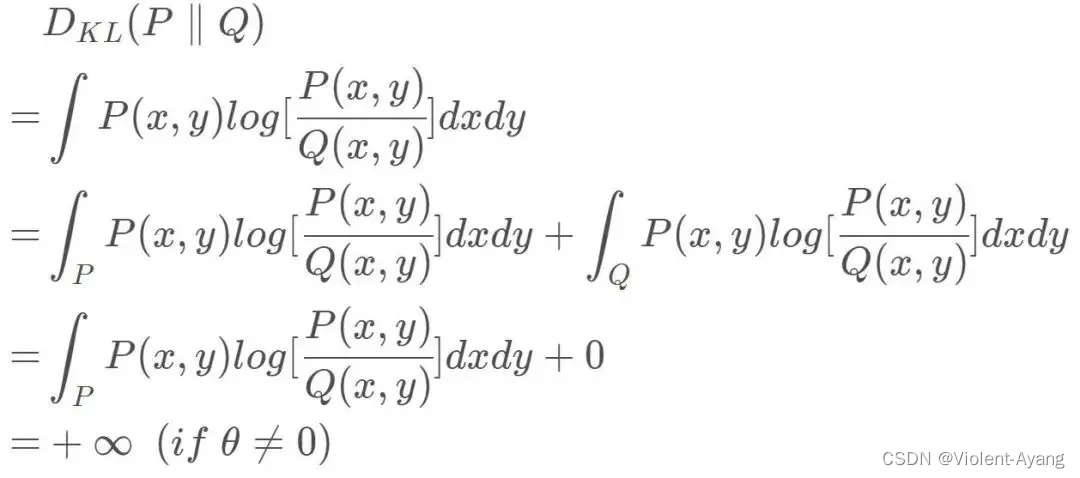
K L ( P 1 ∥ P 2 ) = K L ( P 1 ∣ ∣ P 2 ) = { + ∞ if θ ≠ 0 0 if θ = 0 (突变) J S ( P 1 ∥ P 2 ) = { log 2 if θ ≠ 0 0 if θ − 0 (突变 ) W ( P 0 , P 1 ) = ∣ θ ∣ (平滑 ) \begin{aligned} & K L\left(P_1 \| P_2\right)=K L\left(P_1|| P_2\right)=\left\{\begin{array}{ll} +\infty & \text { if } \theta \neq 0 \\ 0 & \text { if } \theta=0 \end{array}\right. \text { (突变) } \\ & J S\left(P_1 \| P_2\right)=\left\{\begin{array}{ll} \log 2 & \text { if } \theta \neq 0 \\ 0 & \text { if } \theta-0 \end{array}\right. \text { (突变 ) } \\ & W\left(P_0, P_1\right)=|\theta| \text { (平滑 ) } \end{aligned} KL(P1∥P2)=KL(P1∣∣P2)={+∞0 if θ=0 if θ=0 (突变) JS(P1∥P2)={log20 if θ=0 if θ−0 (突变 ) W(P0,P1)=∣θ∣ (平滑 )
第四部分:从 Wasserstein 距离到 WGAN
EMD ( P r , P θ ) = inf γ ∈ Π ∑ x , y ∥ x − y ∥ γ ( x , y ) = inf γ ∈ Π E ( x , y ) ∼ γ ∥ x − y ∥ \operatorname{EMD}\left(P_r, P_\theta\right)=\inf _{\gamma \in \Pi} \sum_{x, y}\|x-y\| \gamma(x, y)=\inf _{\gamma \in \Pi} \mathbb{E}_{(x, y) \sim \gamma}\|x-y\| EMD(Pr,Pθ)=γ∈Πinfx,y∑∥x−y∥γ(x,y)=γ∈ΠinfE(x,y)∼γ∥x−y∥
It is intractable to exhaust all the possible joint distributions in
Π
(
p
r
,
p
g
)
\Pi\left(p_r, p_g\right)
Π(pr,pg) to compute
inf
γ
∼
Π
(
p
r
,
p
g
)
\inf _{\gamma \sim \Pi\left(p_r, p_g\right)}
infγ∼Π(pr,pg) Thus the authors proposed a smart transformation of the formula based on the KantorovichRubinstein duality to: 作者提出了基于 Kantorovich-Rubinstein 对偶性的公式的巧妙转换:
W
(
p
r
,
p
g
)
=
1
K
sup
∥
f
∥
L
≤
K
E
x
∼
p
r
[
f
(
x
)
]
−
E
x
∼
p
g
[
f
(
x
)
]
W\left(p_r, p_g\right)=\frac{1}{K} \sup _{\|f\| L \leq K} \mathbb{E}_{x \sim p_r}[f(x)]-\mathbb{E}_{x \sim p_g}[f(x)]
W(pr,pg)=K1∥f∥L≤KsupEx∼pr[f(x)]−Ex∼pg[f(x)]
首先需要介绍一个概念——Lipschitz 连续。它其实就是在一个连续函数
f
f
f 上面额外施加了一个限 制,要求存在一个常数
K
≥
0
K \geq 0
K≥0 使得定义域内的任意两个元素
x
1
x_1
x1 和
x
2
x_2
x2 都满足
∣
f
(
x
1
)
−
f
(
x
2
)
∣
≤
K
∣
x
1
−
x
2
∣
\left|f\left(x_1\right)-f\left(x_2\right)\right| \leq K\left|x_1-x_2\right|
∣f(x1)−f(x2)∣≤K∣x1−x2∣
此时称函数
f
f
f 的 Lipschitz 常数为
K
K
K 。
上述公式 的意思就是在要求函数
f
f
f 的 Lipschitz 常数
∣
f
∥
L
\mid f \|_L
∣f∥L 不超过
K
K
K 的条件下,对所有可能满足 件的
f
f
f 取到趻 数
w
w
w 来定义一系列可能的函数
f
w
f_w
fw ,此时求解公式 可以近似变成求解如下形式
K
⋅
W
(
P
r
,
P
g
)
≈
max
w
:
∣
f
w
∣
L
≤
K
E
x
∼
P
r
[
f
w
(
x
)
]
−
E
x
∼
P
g
[
f
w
(
x
)
]
K \cdot W\left(P_r, P_g\right) \approx \max _{w:\left|f_w\right|_L \leq K} \mathbb{E}_{x \sim P_r}\left[f_w(x)\right]-\mathbb{E}_{x \sim P_g}\left[f_w(x)\right]
K⋅W(Pr,Pg)≈w:∣fw∣L≤KmaxEx∼Pr[fw(x)]−Ex∼Pg[fw(x)]
W ( p r , p θ ) = inf γ ∈ π ∬ ∥ x − y ∥ γ ( x , y ) d x d y = inf γ ∈ π E x , y ∼ γ [ ∥ x − y ∥ ] . W\left(p_r, p_\theta\right)=\inf _{\gamma \in \pi} \iint\|x-y\| \gamma(x, y) \mathrm{d} x \mathrm{~d} y=\inf _{\gamma \in \pi} \mathbb{E}_{x, y \sim \gamma}[\|x-y\|] . W(pr,pθ)=γ∈πinf∬∥x−y∥γ(x,y)dx dy=γ∈πinfEx,y∼γ[∥x−y∥].
W ( p r , p θ ) = inf γ ∈ π E x , y ∼ γ [ ∥ x − y ∥ ] = inf γ E x , y ∼ γ [ ∥ x − y ∥ + sup f E s ∼ p r [ f ( s ) ] − E t ∼ p θ [ f ( t ) ] − ( f ( x ) − f ( y ) ) ] ⏟ = { 0 , if γ ∈ π + ∞ else = inf γ sup f E x , y ∼ γ [ ∥ x − y ∥ + E s ∼ p r [ f ( s ) ] − E t ∼ p θ [ f ( t ) ] − ( f ( x ) − f ( y ) ) ] \begin{aligned} W\left(p_r, p_\theta\right) & =\inf _{\gamma \in \pi} \mathbb{E}_{x, y \sim \gamma}[\|x-y\|] \\ & =\inf _\gamma \mathbb{E}_{x, y \sim \gamma}[\|x-y\|+\underbrace{\left.\sup _f \mathbb{E}_{s \sim p_r}[f(s)]-\mathbb{E}_{t \sim p_\theta}[f(t)]-(f(x)-f(y))\right]} \\ & =\left\{\begin{array}{c} 0, \text { if } \gamma \in \pi \\ +\infty \text { else } \end{array}\right. \\ & =\inf _\gamma \sup _f \mathbb{E}_{x, y \sim \gamma}\left[\|x-y\|+\mathbb{E}_{s \sim p_r}[f(s)]-\mathbb{E}_{t \sim p_\theta}[f(t)]-(f(x)-f(y))\right] \end{aligned} W(pr,pθ)=γ∈πinfEx,y∼γ[∥x−y∥]=γinfEx,y∼γ[∥x−y∥+ fsupEs∼pr[f(s)]−Et∼pθ[f(t)]−(f(x)−f(y))]={0, if γ∈π+∞ else =γinffsupEx,y∼γ[∥x−y∥+Es∼pr[f(s)]−Et∼pθ[f(t)]−(f(x)−f(y))]
sup f inf γ E x , y ∼ γ [ ∥ x − y ∥ + E s ∼ p r [ f ( s ) ] − E t ∼ p θ [ f ( t ) ] − ( f ( x ) − f ( y ) ) ] = sup f E s ∼ p r [ f ( s ) ] − E t ∼ p θ [ f ( t ) ] + inf γ E x , y ∼ γ [ ∥ x − y ∥ − ( f ( x ) − f ( y ) ) ] ⏟ γ = { 0 , if ∥ f ∥ L ≤ 1 − ∞ else \begin{array}{r} \sup _f \inf _\gamma \mathbb{E}_{x, y \sim \gamma}\left[\|x-y\|+\mathbb{E}_{s \sim p_r}[f(s)]-\mathbb{E}_{t \sim p_\theta}[f(t)]-(f(x)-f(y))\right] \\ =\sup _f \mathbb{E}_{s \sim p_r}[f(s)]-\mathbb{E}_{t \sim p_\theta}[f(t)]+\underbrace{\inf _\gamma \mathbb{E}_{x, y \sim \gamma}[\|x-y\|-(f(x)-f(y))]}_\gamma \\ =\left\{\begin{array}{cc} 0, & \text { if }\|f\|_L \leq 1 \\ -\infty & \text { else } \end{array}\right. \end{array} supfinfγEx,y∼γ[∥x−y∥+Es∼pr[f(s)]−Et∼pθ[f(t)]−(f(x)−f(y))]=supfEs∼pr[f(s)]−Et∼pθ[f(t)]+γ γinfEx,y∼γ[∥x−y∥−(f(x)−f(y))]={0,−∞ if ∥f∥L≤1 else
W ( p r , p θ ) = sup f E s ∼ p r [ f ( s ) ] − E t ∼ p θ [ f ( t ) ] + inf γ E x , y ∼ γ [ ∥ x − y ∥ − ( f ( x ) − f ( y ) ) ] = sup ∥ f ∥ L ≤ 1 E s ∼ p r [ f ( s ) ] − E t ∼ p θ [ f ( t ) ] \begin{aligned} W\left(p_r, p_\theta\right) & =\sup _f \mathbb{E}_{s \sim p_r}[f(s)]-\mathbb{E}_{t \sim p_\theta}[f(t)]+\inf _\gamma \mathbb{E}_{x, y \sim \gamma}[\|x-y\|-(f(x)-f(y))] \\ & =\sup _{\|f\|_{L \leq 1}} \mathbb{E}_{s \sim p_r}[f(s)]-\mathbb{E}_{t \sim p_\theta}[f(t)] \end{aligned} W(pr,pθ)=fsupEs∼pr[f(s)]−Et∼pθ[f(t)]+γinfEx,y∼γ[∥x−y∥−(f(x)−f(y))]=∥f∥L≤1supEs∼pr[f(s)]−Et∼pθ[f(t)]