在卷积神经网络（CNN）中为什么可以使用多个较小的卷积核替代一个较大的卷积核，以达到相同的感受野

flyfish

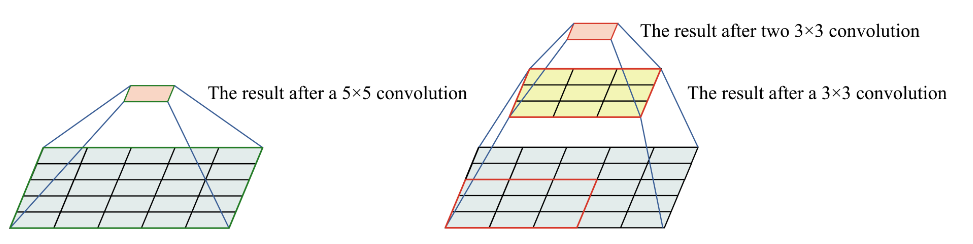
在卷积神经网络（CNN）中，可以使用多个较小的卷积核替代一个较大的卷积核，以达到相同的感受野。具体来说：

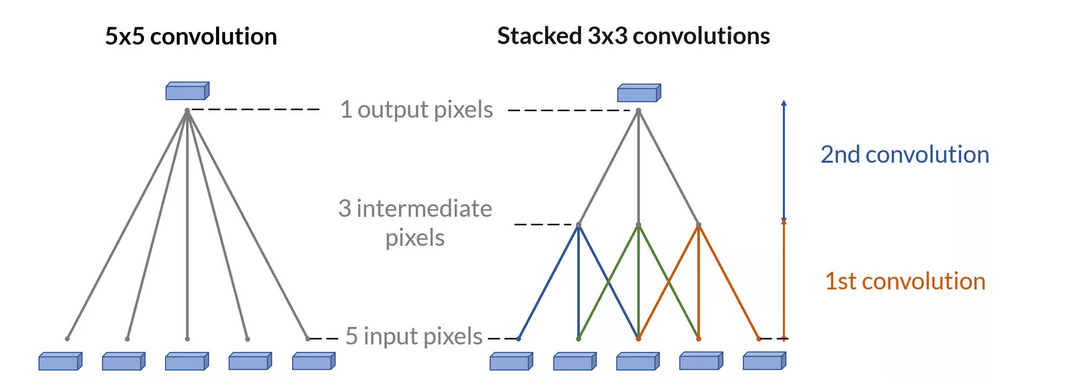
• 两个3x3的卷积核堆叠可以替代一个5x5的卷积核。这样，每个输出单元都能够感受到一个5x5区域的输入信息。

• 三个3x3的卷积核堆叠可以替代一个7x7的卷积核。这意味着，通过三层3x3卷积，最终的输出单元可以感受到一个7x7区域的输入信息。

• 四个3x3的卷积核堆叠可以替代一个9x9的卷积核。通过四层3x3卷积，输出单元能够覆盖一个9x9区域的输入信息。

import numpy as np

# 输入特征图
input_feature_map = np.array([
    [1, 2, 3, 0, 1],
    [4, 5, 6, 1, 2],
    [7, 8, 9, 2, 3],
    [1, 2, 3, 0, 1],
    [4, 5, 6, 1, 2]
])

# 卷积核
kernel = np.array([
    [1, 0, -1],
    [1, 0, -1],
    [1, 0, -1]
])

# 输出特征图的大小
output_height = input_feature_map.shape[0] - kernel.shape[0] + 1
output_width = input_feature_map.shape[1] - kernel.shape[1] + 1
output_feature_map = np.zeros((output_height, output_width))

# 计算总计算量
total_computations = 0

# 进行卷积操作
for i in range(output_height):
    for j in range(output_width):
        # 提取当前窗口的子矩阵
        current_window = input_feature_map[i:i+kernel.shape[0], j:j+kernel.shape[1]]
        # 进行逐元素乘法并求和
        output_feature_map[i, j] = np.sum(current_window * kernel)
        # 计算当前窗口的计算量
        total_computations += np.prod(kernel.shape)  # 3x3 次乘法

print("输出特征图:")
print(output_feature_map)
print("总计算量 (乘法次数):", total_computations)

在进行卷积操作时，对于输入特征图大小 $5\times 5$ 和卷积核大小 $3\times 3$，输出特征图的大小是 $(5-3+1)\times (5-3+1)=3\times 3$。在每个输出位置，我们需要进行 $3\times 3=9$ 次乘法计算，总的计算量是 $3\times 3\times 9=81$ 次乘法。

1 2 3 0 1       1 2 3      2 3 0      3 0 1
4 5 6 1 2       4 5 6      5 6 1      6 1 2
7 8 9 2 3       7 8 9      8 9 2      9 2 3

4 5 6 1 2       4 5 6      5 6 1      6 1 2
7 8 9 2 3       7 8 9      8 9 2      9 2 3
1 2 3 0 1       1 2 3      2 3 0      3 0 1

7 8 9 2 3       7 8 9      8 9 2      9 2 3
1 2 3 0 1       1 2 3      2 3 0      3 0 1
4 5 6 1 2       4 5 6      5 6 1      6 1 2

计算卷积操作的计算量

在计算卷积操作的总计算量时，可以使用以下公式：
$\text{总计算量 (乘法次数)}=(H-K+1)\times (W-K+1)\times K\times K\times C_{in}\times C_{out}$
其中：

• $H$ 和 $W$ 是输入特征图的高度和宽度。

• $K$ 是卷积核的大小（假设为方形，即 $K\times K$）。

• $C_{in}$ 是输入通道数。

• $C_{out}$ 是输出通道数。

应用公式计算示例

对于一个 5x5 的输入特征图和 3x3 的卷积核，假设输入通道数和输出通道数都为 1：

1. 输入特征图大小： $H=5$, $W=5$

2. 卷积核大小： $K=3$

3. 输入通道数： $C_{in}=1$

4. 输出通道数： $C_{out}=1$

将这些值代入公式中：
$$\text{总计算量 (乘法次数)}=(5-3+1)\times (5-3+1)\times 3\times 3\times 1\times 1$$

计算：
$$\text{总计算量 (乘法次数)}=3\times 3\times 3\times 3=81$$

$(H-K+1)\times (W-K+1)$ 计算的是输出特征图的大小，这里是 $3\times 3$。
每个输出特征图的位置上，进行 $K\times K\times C_{in}$ 次乘法计算，这里是 $3\times 3\times 1=9$ 次乘法。
计算量是输出特征图的元素数量乘以每个元素的计算量，即 $9\times 9=81$ 次乘法。

例子

如果输入特征图是 $28\times 28$，计算两个 3x3 卷积核堆叠和一个 5x5 卷积核的计算量，并比较它们。

情况 1：两个 3x3 卷积核堆叠

1. 第一个 3x3 卷积核 ：

• 输入特征图大小： $28\times 28$

• 输出特征图大小： $(28-3+1)\times (28-3+1)=26\times 26$

• 计算量： $26\times 26\times 3\times 3\times C_{in}\times C_{mid}$

2. 第二个 3x3 卷积核 ：

• 输入特征图大小： $26\times 26$

• 输出特征图大小： $(26-3+1)\times (26-3+1)=24\times 24$

• 计算量： $24\times 24\times 3\times 3\times C_{mid}\times C_{out}$
  ${\text{计算量}}_{3\times 3}=26\times 26\times 9\times C_{in}\times C_{mid}+24\times 24\times 9\times C_{mid}\times C_{out}$

情况 2：一个 5x5 卷积核

• 输入特征图大小： $28\times 28$

• 输出特征图大小： $(28-5+1)\times (28-5+1)=24\times 24$

• 计算量： $24\times 24\times 5\times 5\times C_{in}\times C_{out}$

示例计算

假设输入和输出通道数都为 1：

1. 第一个 3x3 卷积核 ：

• 输出特征图大小： $26\times 26$

• 计算量： $26\times 26\times 9\times 1\times 1=6084$

2. 第二个 3x3 卷积核 ：

• 输出特征图大小： $24\times 24$

• 计算量： $24\times 24\times 9\times 1\times 1=5184$
  总计算量：
  ${\text{计算量}}_{3x3}=6084+5184=11268$

1. 一个 5x5 卷积核 ：

• 输出特征图大小： $24\times 24$

• 计算量： $24\times 24\times 25\times 1\times 1=14400$

def compute_3x3_stack_computation(H, W, C_in, C_out):
    # 第一个 3x3 卷积核
    output_height1 = H - 3 + 1
    output_width1 = W - 3 + 1
    computation_3x3_1 = output_height1 * output_width1 * 3 * 3 * C_in * C_out
    
    # 第二个 3x3 卷积核
    output_height2 = output_height1 - 3 + 1
    output_width2 = output_width1 - 3 + 1
    computation_3x3_2 = output_height2 * output_width2 * 3 * 3 * C_out * C_out
    
    total_computation_3x3 = computation_3x3_1 + computation_3x3_2
    return total_computation_3x3

def compute_5x5_computation(H, W, C_in, C_out):
    # 一个 5x5 卷积核
    output_height = H - 5 + 1
    output_width = W - 5 + 1
    computation_5x5 = output_height * output_width * 5 * 5 * C_in * C_out
    return computation_5x5

# 示例参数
H, W, C_in, C_out = 28, 28, 1, 1

# 计算
computation_3x3 = compute_3x3_stack_computation(H, W, C_in, C_out)
computation_5x5 = compute_5x5_computation(H, W, C_in, C_out)

# 减少的计算量百分比
reduction_percentage = (1 - computation_3x3 / computation_5x5) * 100

print("两个 3x3 卷积核堆叠的计算量:", computation_3x3)
print("一个 5x5 卷积核的计算量:", computation_5x5)
print("减少的计算量百分比:", reduction_percentage)

两个 3x3 卷积核堆叠的计算量: 11268
一个 5x5 卷积核的计算量: 14400
减少的计算量百分比: 21.750000000000004
参考论文《Rethinking the Inception Architecture for Computer Vision》