1. 二叉树的中序遍历
- 题目描述
给定一个二叉树,返回它的中序遍历。 - 解题思路
使用递归的方法对左子树进行中序遍历,然后访问根节点,最后对右子树进行中序遍历。也可以使用栈来模拟递归的过程,迭代地进行中序遍历。 - 代码
class Solution: def inorderTraversal(self, root: Optional[TreeNode]) -> List[int]: path = [] def dfs(node): nonlocal path if not node: return dfs(node.left) path.append(node.val) dfs(node.right) dfs(root) return path
2. 二叉树的最大深度
- 题目描述
给定一个二叉树,找出其最大深度。最大深度是从根节点到最远叶子节点的最长路径上的节点数。 - 解题思路
使用递归方法计算左右子树的最大深度,然后取最大值加一。也可以使用广度优先搜索(BFS)遍历树的每一层,记录层数。 - 代码
class Solution: def maxDepth(self, root: Optional[TreeNode]) -> int: if not root: return 0 left = self.maxDepth(root.left) right = self.maxDepth(root.right) return max(left, right) + 1
3. 翻转二叉树
-
题目描述
镜像翻转一棵二叉树。
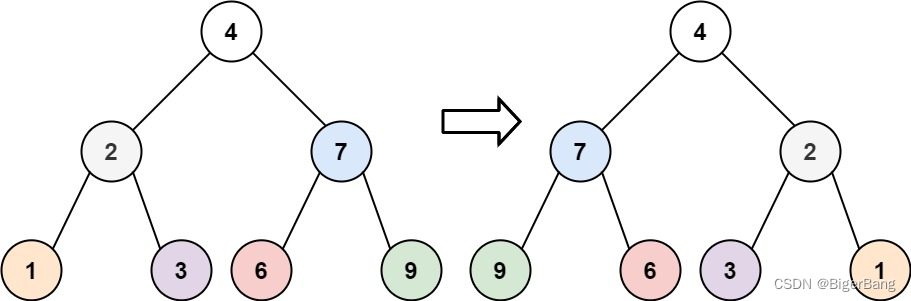
-
解题思路
可以看到翻转二叉树就是对所有节点的左右节点进行翻转,因此使用递归方法交换每个节点的左右子节点。 -
代码
class Solution: def invertTree(self, root: Optional[TreeNode]) -> Optional[TreeNode]: if not root: return None invert_left = self.invertTree(root.left) invert_right = self.invertTree(root.right) root.left, root.right = invert_right, invert_left return root
4. 对称二叉树
-
题目描述
给定一个二叉树,检查它是否是镜像对称的。
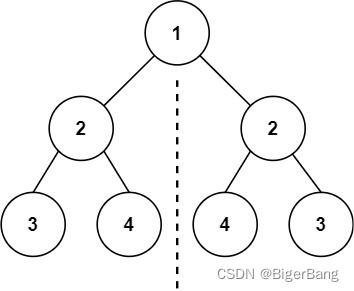
-
解题思路
观察发现二叉树对称就是,比较左节点的左节点和右节点的右节点是否相同,左节点的右节点和右节点的左节点是否相同。此题特殊在需要写一个辅助函数,输入是两个节点,并从root.left和root.right开始递归 -
代码
class Solution: def isSymmetric(self, root: Optional[TreeNode]) -> bool: def symmetric(left, right): if not left and not right: return True if not left or not right: return False if left.val != right.val: return False return symmetric(left.left, right.right) and symmetric(left.right, right.left) return symmetric(root.left, root.right)
5. 二叉树的直径
- 题目描述
给定一棵二叉树,计算它的直径。二叉树的直径是树中任意两个节点路径长度中的最大值。 - 解题思路
使用递归方法计算每个节点的左右子树深度,然后更新最大直径。每个节点的直径是左右子树深度之和,注意直径的定义是边的数量而不是节点数。 - 代码
class Solution: def diameterOfBinaryTree(self, root: Optional[TreeNode]) -> int: res = 0 def max_height(root): nonlocal res if not root: return 0 left = max_height(root.left) right = max_height(root.right) res = max(res, left + right) return max(left, right) + 1 max_height(root) return res
6. 二叉树的层序遍历
- 题目描述
给定一个二叉树,返回其按层次遍历的节点值。即逐层地,从左到右访问所有节点。 - 解题思路
使用队列进行广度优先搜索(BFS),逐层访问每个节点,并将节点值存入结果列表。注意在将读取的每个节点的左右节点压入队列的时候,要记得判断左右节点是不是None; - 代码
class Solution: def levelOrder(self, root: Optional[TreeNode]) -> List[List[int]]: if not root: return [] que = deque() que.append(root) res = [] while len(que) != 0: cur_level = [] n = len(que) for i in range(n): node = que.popleft() cur_level.append(node.val) # 注意要判断节点是不是None,避免将None加入到que if node.left: que.append(node.left) if node.right: que.append(node.right) res.append(cur_level) return res
7. 将有序数组转换为二叉搜索树
- 题目描述
将一个按照升序排序的有序数组转换为一棵高度平衡的二叉搜索树。 - 解题思路
使用递归方法,每次选择中间元素作为根节点,左右子数组分别作为左右子树,递归构造二叉搜索树。 - 代码
class Solution: def sortedArrayToBST(self, nums: List[int]) -> Optional[TreeNode]: n = len(nums) if n == 0: return None if n == 1: return TreeNode(val = nums[0]) mid = n // 2 node = TreeNode(val = nums[mid]) node.left = self.sortedArrayToBST(nums[: mid]) node.right = self.sortedArrayToBST(nums[mid+1: ]) return node
8. 验证二叉搜索树
- 题目描述
给定一个二叉树,判断其是否是一个有效的二叉搜索树(BST)。 - 解题思路
==二叉搜索树的性质:中序遍历是有序的。==因此对二叉搜索树进行中序遍历,利用一个全局变量来记录上一节点的值,这样遍历所有节点并检查节点值是否严格递增。 - 代码
class Solution: def isValidBST(self, root: Optional[TreeNode]) -> bool: # 设置全局变量,用于记录上一个节点的值 last_val = float("-inf") # 中序遍历 def inorder(root): nonlocal last_val if not root: return True # 查验左子树是不是二叉搜索树 left = inorder(root.left) # 查验当前节点 if root.val <= last_val: return False last_val = root.val # 查验右子树 right = inorder(root.right) return left and right return inorder(root)
9. 二叉搜索树中第K小的元素
- 题目描述
给定一个二叉搜索树,编写一个函数 kthSmallest 来查找其中第 k 个最小的元素。 - 解题思路
依然是利用二叉搜索树的性质,使用中序遍历二叉搜索树,计数遍历到第 k 个节点时,即为第 k 小的元素。 - 代码
class Solution:
def kthSmallest(self, root: Optional[TreeNode], k: int) -> int:
def dfs(root):
if not root: return
dfs(root.left)
if self.k == 0: return
self.k -= 1
if self.k == 0: self.res = root.val
dfs(root.right)
self.k = k
dfs(root)
return self.res
10. 二叉树的右视图
- 题目描述
给定一棵二叉树,想象自己站在它的右侧,按从顶部到底部的顺序,返回看到的节点值。 - 解题思路
使用广度优先搜索(BFS),逐层记录最后一个节点的值。 - 代码
class Solution: def rightSideView(self, root: Optional[TreeNode]) -> List[int]: if not root: return [] que = deque() que.append(root) res = [] while len(que) != 0: n = len(que) for i in range(n): node = que.popleft() if i == n - 1: res.append(node.val) if node.left: que.append(node.left) if node.right: que.append(node.right) return res
11. 二叉树展开为链表
-
题目描述
给定一个二叉树,原地将它展开为一个单链表,链表的顺序和先序遍历相同。
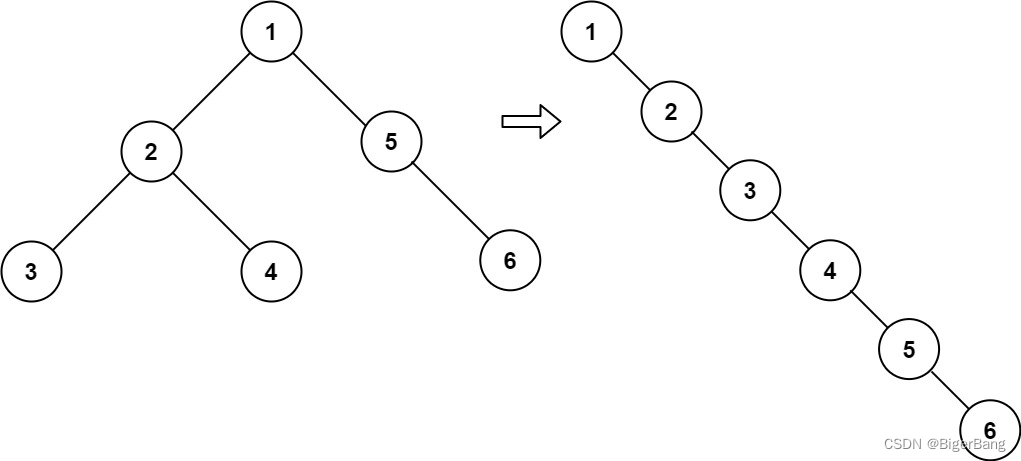
-
解题思路
对二叉树进行先序遍历,然后把遍历到的节点依次连接起来,使用一个全局变量记录上一个节点; -
代码
class Solution: def flatten(self, root: Optional[TreeNode]) -> None: """ Do not return anything, modify root in-place instead. """ if not root: return dummy_root = TreeNode() prev = dummy_root def dfs(node): nonlocal prev if not node: return # 这里要先吧left和right保存下来 left = node.left right = node.right prev.right = node prev.left = None prev = node dfs(left) dfs(right) dfs(root)
12. 从前序与中序遍历序列构造二叉树
- 题目描述
根据一棵树的前序遍历与中序遍历构造二叉树。 - 解题思路
使用递归方法,前序遍历的第一个元素为根节点,根据根节点的值找到中序遍历中根节点的位置,然后就能根据中序遍历分割左右子树的节点,将两个遍历分成左右两部分,递归构造二叉树。 - 代码
class Solution:
def buildTree(self, preorder: List[int], inorder: List[int]) -> Optional[TreeNode]:
if len(preorder) == 0:
return None
if len(preorder) == 1:
return TreeNode(val=preorder[0])
root_val = preorder[0]
# 在中序遍历中从下标为0开始寻找
i = 0
while inorder[i] != root_val:
i += 1
root = TreeNode(root_val)
root.left = self.buildTree(preorder[1:i+1], inorder[:i])
root.right = self.buildTree(preorder[i+1:], inorder[i+1:])
return root
13. 路径总和 III
-
题目描述
给定一个二叉树,它的每个节点都存放一个整数值。找出路径和等于给定数值的路径总数。路径不需要从根节点开始,也不需要在叶子节点结束,但是路径方向必须是向下的(只能从父节点到子节点)。
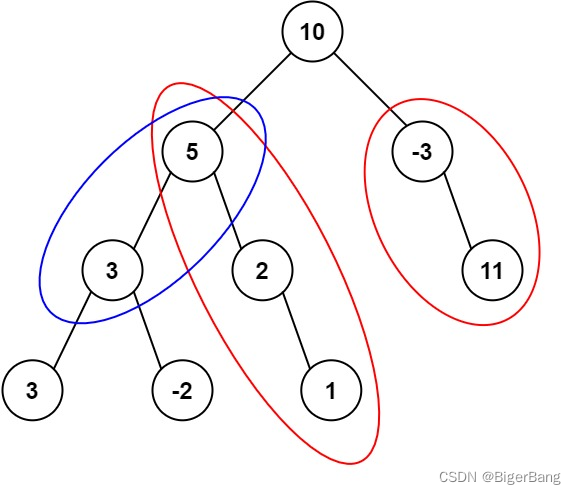
-
解题思路
使用双重递归,外层递归遍历每个节点,内层递归计算以当前节点为起点的路径数。 -
代码
class Solution: def pathSum(self, root: Optional[TreeNode], targetSum: int) -> int: res = 0 # 计算以当前节点为起点的路径数 def backtrace(node, s, targetSum): nonlocal res if not node: return s += node.val if s == targetSum: res += 1 backtrace(node.left, s, targetSum) backtrace(node.right, s, targetSum) s -= node.val # 递归遍历每个节点 def dfs(root, targetSum): if not root: return backtrace(root, 0, targetSum) dfs(root.left, targetSum) dfs(root.right, targetSum) dfs(root, targetSum) return res
14. 二叉树的最近公共祖先
- 题目描述
给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。 - 解题思路
使用递归方法,如果当前节点为目标节点之一或为空,则返回当前节点;否则,递归查找左右子树的最近公共祖先。如果左右子树都找到目标节点,则当前节点为最近公共祖先。 - 代码
class Solution: def lowestCommonAncestor(self, root: 'TreeNode', p: 'TreeNode', q: 'TreeNode') -> 'TreeNode': if not root: return root if root == p or root == q: return root left = self.lowestCommonAncestor(root.left, p, q) right = self.lowestCommonAncestor(root.right, p, q) if left and right: return root if left: return left if right: return right return None
15. 二叉树中的最大路径和
-
题目描述
给定一个非空二叉树,返回其最大路径和。路径被定义为一条从树中任意节点出发,沿父节点-子节点连接,达到任意节点的序列。该路径至少包含一个节点,且不一定经过根节点。 -
解题思路
经过某个节点cur的最大路径和 = cur.val + max(cur.left起始的路径最大和, 0) + max(cur.right起始的路径最大和,0)。使用双层递归,内层递归求以当前节点为起始节点的路径最大和,外层递归遍历所有节点,根据上面的公式求取最终结果; -
代码
class Solution: def maxPathSum(self, root: Optional[TreeNode]) -> int: # 求以当前节点为起始节点的路径最大和 def backtrace(root): if not root: return 0 left = backtrace(root.left) right = backtrace(root.right) if left <= 0 and right <= 0: return root.val return root.val + max(left, right) # 外层递归遍历所有节点,根据上面的公式求取最终结果 def dfs(root): nonlocal res if not root: return left = backtrace(root.left) right = backtrace(root.right) cur = root.val if left > 0: cur += left if right > 0: cur += right res = max(cur, res) dfs(root.left) dfs(root.right) res = float("-inf") dfs(root) return res
16. 总结
- 递归分解成子问题
这一类问题可以递归将一个二叉树分解成左右子树,分别进行相同的问题求解,依次类推;这类问题包括二叉树的最大深度、翻转二叉树、对称二叉树 - 二叉搜索树
重要性是中序遍历是升序的 - 层序遍历
队列