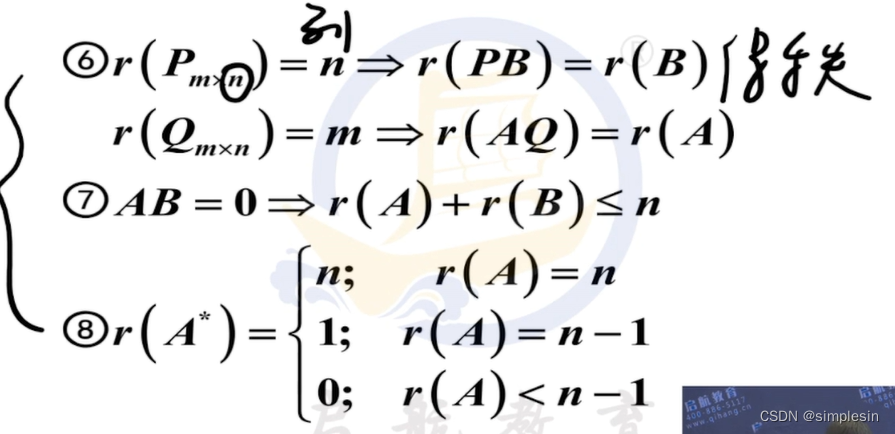what（是什么）

反向传播算法（Backpropagation）是一种用于训练人工神经网络的常见方法。它通过计算网络预测与实际结果之间的误差，然后反向传播这个误差来调整网络中每个权重的值，从而逐步优化网络的学习过程

where（用在哪）

绝大多数的神经网络都会使用反向传播算法进行网络权重以及阈值的更新，简单列举部分典型的使用场景如下

How（原理&&怎么用）

原理以及推导过程

下面重点介绍反向传播算法的推导流程

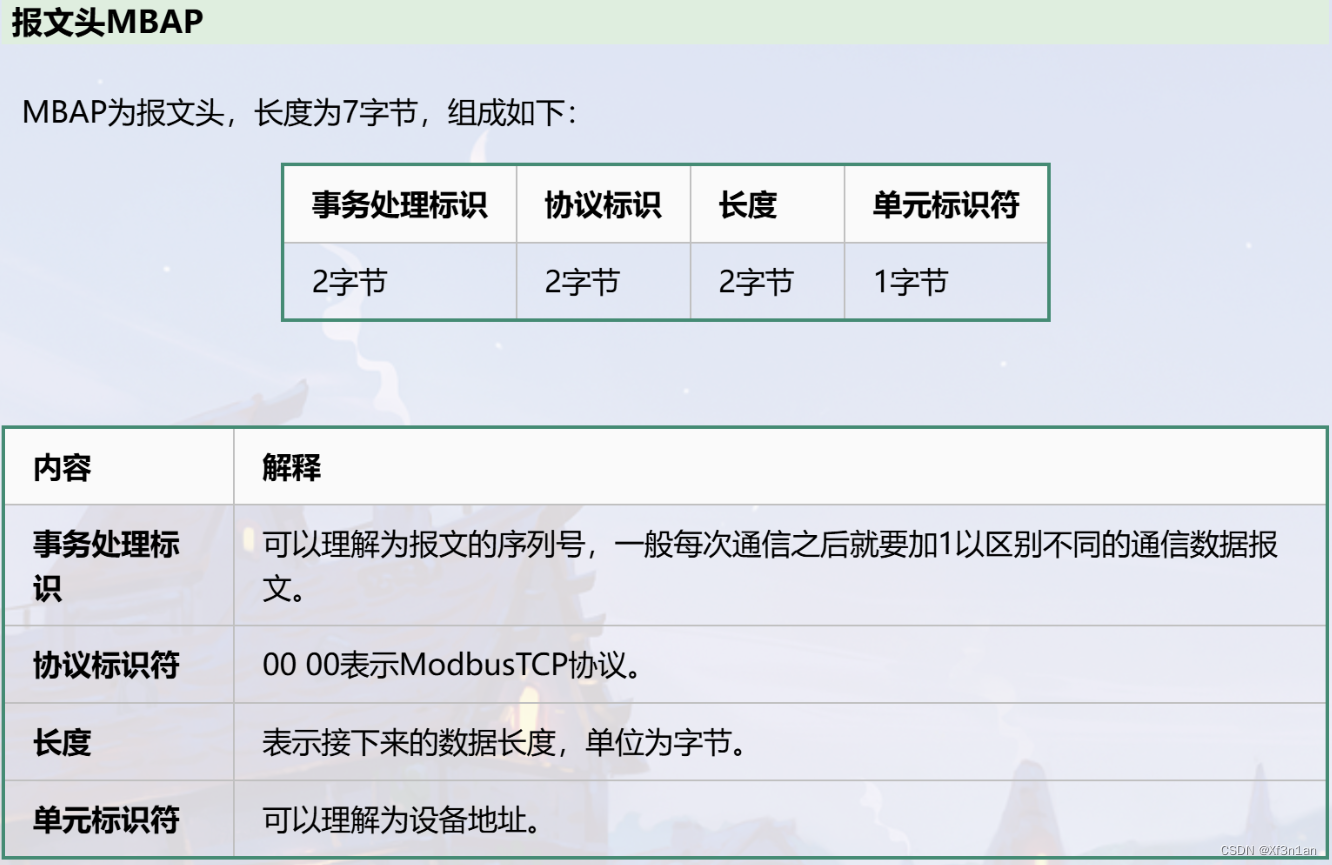
假设有以上简单的神经网路模型，分为输入层、隐藏层、输出层。其中隐藏层包括4个神经元、输出层包括2个神经元。
假设输出层的两个神经元为$y_1$，$y_2$，其激活阈值分别为$\beta$，$\gamma$，两个神经元的输入分别为$y_{1in}$，$y_{2in}$，输出分别为$\widehat{y_1}$和$\widehat{y_2}$。
假设隐藏层四个神经元为$h_1$，$h_2$，$h_3$，$h_4$，其中$h_1$的激活阈值为$\delta$，神经元$h_1$的输入值为$h_{in}$，输出值为$h_{out}$。
假设输入层两个神经元为$x_1$，$x_2$，其中神经元$x_1$的输出为$x_{out}$。
假设神经元$x_1$到神经元$h_1$的连接权重为$W_{11}$，神经元$h_1$到神经元$y_1$、$y_2$的连接权重分别为$W_{21}$、$W_{22}$。
假设神经元的激活函数为sigmoid函数，sigmoid激活函数的表达式：
$$f(x)=\frac{1}{1-e^{-x}}$$
该激活函数有一个非常好的性质：
$$f^{\prime }(x)=f(x)(1-f(x))$$
下面，详细介绍连接权重$W$以及激活阈值的更新过程。
首先，给出$W_{21}$以及$\beta$的更新公式，其中，$W_{21}$更新公式为：
$$W_{21}=W_{21}+\eta \ast \Delta W_{21}$$
同理，$\beta$更新公式为：
$$\beta =\beta +\eta \ast \Delta \beta$$

在以上公式中，只有$\Delta W_{21}$以及$\Delta \beta$未知，需要计算。而已知的是样本，也就是$(x,y)$，那么我们将通过样本数据来表达出上述$\Delta W_{21}$以及$\Delta \beta$。
根据反向传播算法，$\Delta W_{21}$以及$\Delta \beta$分别为最终的误差对$W_{21}$以及$\beta$的偏导数。假设采用的损失函数为：
$$Loss=\frac{1}{2}(y_1-\widehat{y_1}{)}^2+\frac{1}{2}(y_2-\widehat{y_2}{)}^2$$
扩展到输出层有k个神经元的情况：
$$Loss=\frac{1}{2}{\Sigma }_1^k(y_i-\widehat{y_i}{)}^2$$
而从输出端看，能得到以下表达式：
$$\widehat{y_1}=f(y_{1in}-\beta )=f(W_{21}{h}_{out}-\beta )$$
将$\widehat{y_1}$带入到损失函数中，也就是：
$$Loss=\frac{1}{2}(y_1-f(W_{21}{h}_{out}-\beta ){)}^2+\frac{1}{2}(y_2-f(W_{22}{h}_{out}-\gamma ){)}^2$$
如此，便得出损失和$W_{21}$之间的代数关系式，接下来只需要对该表达式求导即可得到$\Delta W_{21}$以及$\Delta \beta$。

首先，$\frac{\partial Loss}{\partial W_{21}}$的计算公式为:
$$\begin{array}{rl}\frac{\partial Loss}{\partial W_{21}}& =[y_1-f(W_{21}{h}_{out}-\beta )]\ast [-f^{\prime }(W_{21}{h}_{out}-\beta )]\ast h_{out}\\ & =-[y_1-f(W_{21}{h}_{out}-\beta )]\ast f(W_{21}{h}_{out}-\beta )[1-(f(W_{21}{h}_{out}-\beta ))]\ast h_{out}\\ & =-(y_1-\widehat{y_1})\ast \widehat{y_1}\ast (1-\widehat{y_1})\ast h_{out}\end{array}$$
同样地，$\frac{\partial Loss}{\partial \beta }$的计算公式为：
$$\begin{array}{rl}\frac{\partial Loss}{\partial \beta }& =[y_1-f(W_{21}{h}_{out}-\beta )]\ast [-f^{\prime }(W_{21}{h}_{out}-\beta )]\ast (-1)\\ & =[y_1-f(W_{21}{h}_{out}-\beta )]\ast f(W_{21}{h}_{out}-\beta )[1-(f(W_{21}{h}_{out}-\beta ))]\\ & =(y_1-\widehat{y_1})\ast \widehat{y_1}\ast (1-\widehat{y_1})\end{array}$$
由于梯度下降法，需要沿着负梯度方向，所以，$\Delta W_{21}=-\frac{\partial Loss}{\partial W_{21}}$，$\Delta \beta =-\frac{\partial Loss}{\partial \beta }$，从而得出$W_{21},\beta$的更新公式为：
$$\begin{array}{rl}{W}_{21}& =W_{21}+\eta \ast \Delta W_{21}\\ & =W_{21}-\eta \ast \frac{\partial Loss}{\partial W_{21}}\\ & =W_{21}+\eta \ast (y_1-\widehat{y_1})\ast \widehat{y_1}\ast (1-\widehat{y_1})\ast h_{out}\end{array}$$

$$\begin{array}{rl}\beta & =\beta +\eta \ast \Delta \beta \\ & =\beta -\eta \ast \frac{\partial Loss}{\partial \beta }\\ & =\beta -\eta \ast (y_1-\widehat{y_1})\ast \widehat{y_1}\ast (1-\widehat{y_1})\end{array}$$

使用同样的方式，可以对$W_{11},\delta$的梯度公式进行计算和更新。

pytorch中的反向传播

下面举例说明在pytorch中，如何使用反向传播算法来更新权重以及阈值。

import torch
import torch.nn as nn
import torch.optim as optim
import torch.nn.functional as F

# 定义一个复杂的神经网络
class ComplexNet(nn.Module):
    def __init__(self):
        super(ComplexNet, self).__init__()
        self.fc1 = nn.Linear(10, 50)  # 输入大小为10，输出大小为50
        self.fc2 = nn.Linear(50, 20)  # 输入大小为50，输出大小为20
        self.fc3 = nn.Linear(20, 1)   # 输入大小为20，输出大小为1

    def forward(self, x):
        x = F.relu(self.fc1(x))  # 使用ReLU作为激活函数
        x = F.relu(self.fc2(x))
        x = self.fc3(x)
        return x

# 创建网络实例
model = ComplexNet()

# 定义损失函数
criterion = nn.MSELoss()

# 随机生成一些输入和目标输出数据
input_data = torch.randn((32, 10))  # 32个样本，每个样本特征数为10
target_output = torch.randn((32, 1))  # 对应的32个目标输出

# 定义优化器
optimizer = optim.Adam(model.parameters(), lr=0.01)

# 训练模型
model.train()	# 设置模型为训练模式
epochs = 1000
for epoch in range(epochs):
    # 梯度清零
    optimizer.zero_grad()

    # 前向传播
    output = model(input_data)

    # 计算损失
    loss = criterion(output, target_output)

    # 反向传播
    loss.backward()

    # 更新模型参数
    optimizer.step()

    # 每隔一段时间输出一下损失值
    if (epoch+1) % 100 == 0:
        print(f'Epoch [{epoch+1}/{epochs}], Loss: {loss.item():.4f}')

# 打印模型结构
print(model)

在pythrch中，输入在流经每一个神经元时，会构建一个动态计算图（与tensorflow不同，tensorflow为静态计算图），记录了每个神经元的输入输出信息。在反向传播时， loss.backward()会根据已知的样本数据以及神经元的输入输出信息，计算连接权重以及阈值的梯度，然后optimizer.step()来实现对权重和阈值的更新。需要注意的是，在每一个mini-batch开始前，需要使用optimizer.zero_grad()对梯度置零。