看Boyd的凸优化看到这样一个证明：

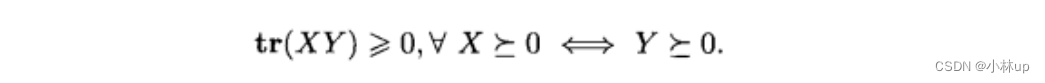
从左到右的证明是

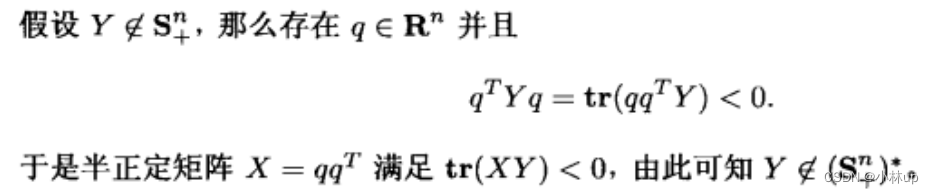
使用了一个逆否命题的方法进行证明，有点忘记了原命题和逆否命题之间的相互转换，记录一下。

简单形式命题

简单形式命题没有全称量词$\forall$和存在两次$\exists$，也没有或与非$\vee$$\wedge$：若p, 则q形式

先从简单的例子出发，比如原命题【$若p,则q$】：

如果一只鸡会下蛋，那么它是母鸡。

逆否命题【$若\neg q,则\neg p$】：

如果一只鸡不是母鸡，那么它不会下蛋。

简单形式命题
$$p\to q\iff \neg q\to \neg p$$
$$p\to \neg q\iff q\to \neg p$$
$$\neg p\to q\iff \neg q\to p$$
$$\neg p\to \neg q\iff q\to p$$

|
前后都进行否定，然后颠倒顺序。

全称量词&存在量词

$\forall x\in M,p(x)$的否定：$$\exists x_0\in M,\neg p(x_0)$$

$\forall x\in M,\neg p(x)$的否定：$$\exists x_0\in M,p(x_0)$$

$\exists x_0\in M,p(x_0)$的否定：$$\forall x\in M,\neg p(x)$$

$\exists x_0\in M,\neg p(x_0)$的否定：$$\forall x\in M,p(x)$$

否定时全称量词和存在量词互改，其后的命题改为命题的否定。

我们再举母鸡的例子，比如原命题【$若\forall x\in M,p(x),则q$】：

对于任意鸡，如果这只鸡会下蛋，那么它是母鸡。

这里可以把$\forall x\in M,p(x)$看作一个命题。我们只需要进行命题的否定。逆否命题就是【$若\neg q,则\exists x_0\in M,\neg p(x_0)$】

如果一只鸡不是母鸡，那么存在一只这样的鸡，它不会下蛋。

逻辑词 与&或

$p\wedge q$的否定：$$\neg (p\wedge q)\iff \neg p\vee \neg q$$

$p\wedge \neg q$的否定：$$\neg (p\wedge \neg q)\iff \neg p\vee q$$

$\neg p\wedge q$的否定：$$\neg (\neg p\wedge q)\iff p\vee \neg q$$

$\neg p\wedge \neg q$的否定：$$\neg (\neg p\wedge \neg q)\iff p\vee q$$

否定时把与和或逻辑词互换，将括号内的每一项都换成否定即可。

我们还是举母鸡的例子，比如原命题【$若\forall x\in M,p(x),则q\wedge r$】：

对于任意鸡，如果这只鸡会下蛋，那么它是母鸡而且已经成年。

逆否命题就是找一个反例【$若\neg q\vee \neg r,则\exists x_0\in M,\neg p(x_0)$】

如果一只鸡不是母鸡或一只鸡没有成年，那么存在一只这样的鸡，它不会下蛋。