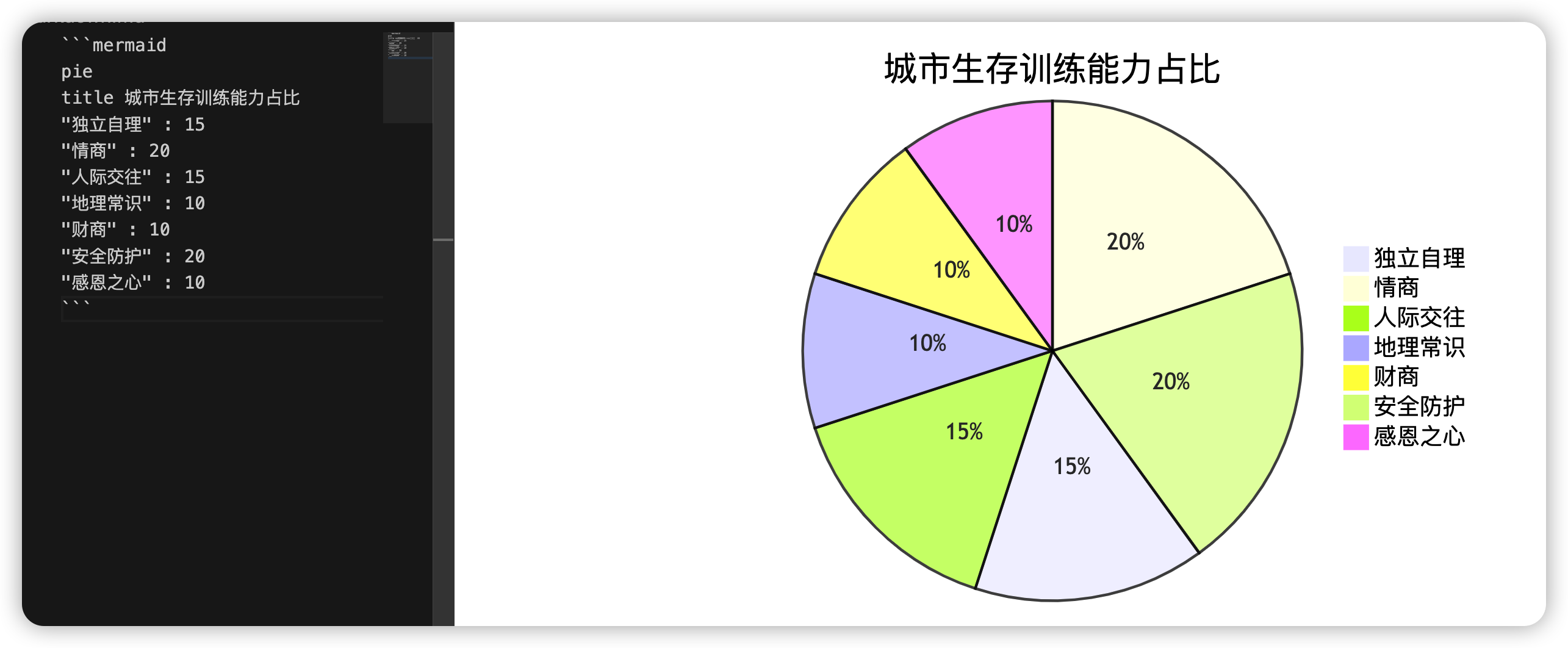
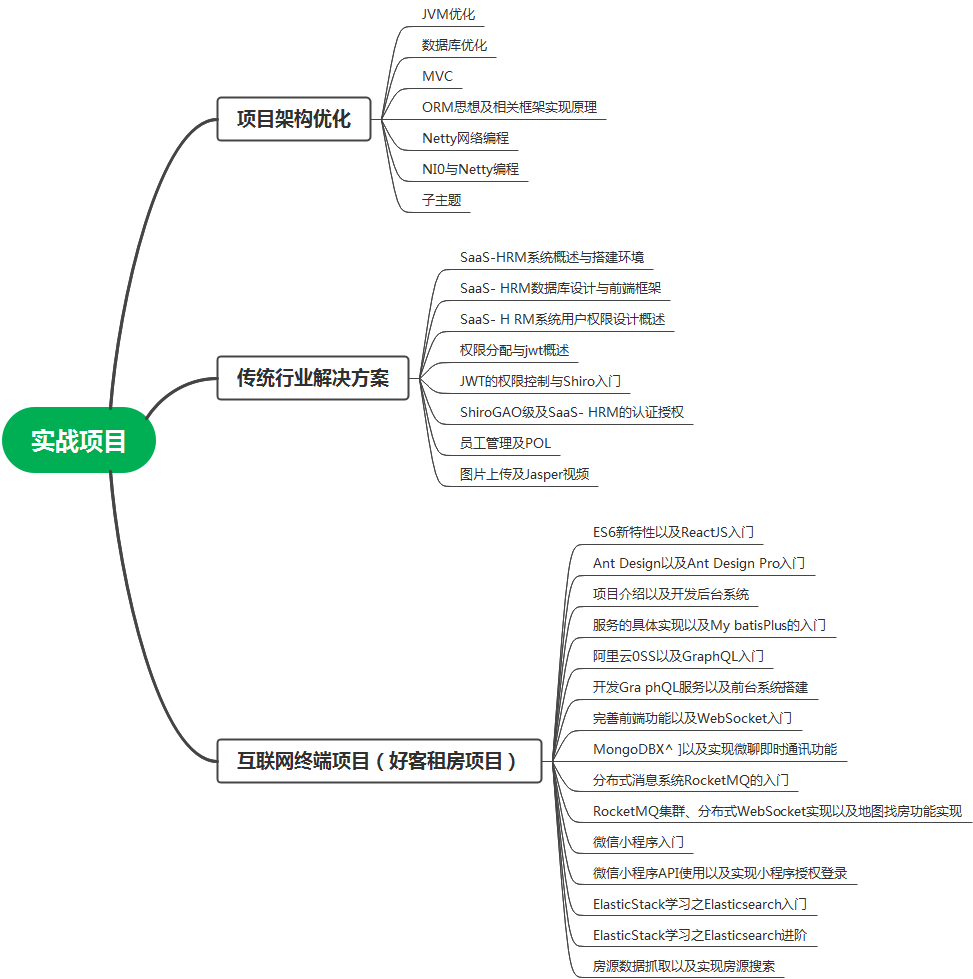
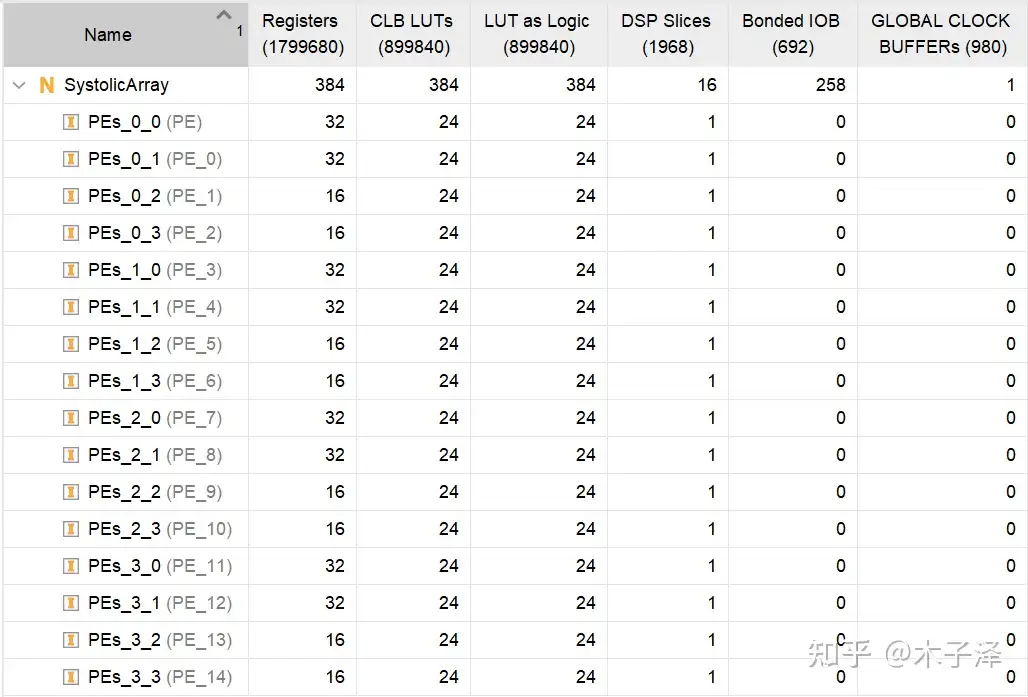
思路：

先转转转，把答案变成求每种数的出现次数都小于i的方案书除以$C_{n+m-1}^m$
对于每个1到m中的数，设每个数的出现次数为xi，则所有x加起来要等于m，且都小于i。
容斥，设其中k个不小于i，则$(-1{)}^k$为容斥系数
k的范围容易得到为0到m/i/k，先把其中ik分给这k个数，方案数为$C_n^k$，然后剩下m-ik继续分，用组合数学技巧得出方案数为$C_{n+m-i\ast k-1}^{m-i\ast k}$
那么答案就是
$$ans=\sum _{i=1}^m(1-\frac{{\sum }_{k=0}^{\lfloor \frac{m}{i}\rfloor }[(-1{)}^k{C}_n^k{C}_{n+m-i\ast k-1}^{m-i\ast k}]}{C_{n+m-1}^m})$$
然后递推预处理组合数，就能在$O(mlogm)$的时间通过此题

$code$

#include<iostream>
#include<cstdio>
#include<cstring>
#define ll long long

using namespace std;

const ll MAXN = 5e5 + 10;

ll p, ans;
ll c[MAXN], c2[MAXN], inv[MAXN];

ll qpow(ll x, ll k) {
	ll ans = 1;
	for(; k; k >>= 1, x = x * x % p) if(k & 1) ans = ans * x % p;
	return ans;
}

void solve() {
	ll n, m;
	scanf("%lld%lld", &m, &n);
	c[0] = 1ll, c2[0] = 1ll;
	for(ll i = 1; i <= m; i ++) {
		c[i] = c[i - 1] * (n - i + 1) % p * inv[i] % p;
		c2[i] = c2[i - 1] * (n + i - 1) % p * inv[i] % p;
	}
	ll ans = 0ll, g = c2[m];
	for(ll i = 1; i <= m; i ++) {
		ll o = 1ll;
		for(ll k = 0; k <= m / i; k ++) { 
			ans += o * c[k] * c2[m - i * k] % p;
			ans %= p;
			o = -o;
		}
	}
	printf("%lld\n", (m - ans * qpow(g, p - 2) % p + p) % p);
}

int main() {
	freopen("mode.in", "r", stdin);
	freopen("mode.out", "w", stdout);
	ll t;
	scanf("%lld%lld", &t, &p);
	inv[1] = 1;
	for(ll i = 2; i <= 200000; i ++) inv[i] = qpow(i, p - 2);
	while(t --) {
		solve();
	}
	return 0;
}