大家好,我是微学AI,今天给大家介绍一下机器学习实战20-利用AnoSVGD算法探索多指标的异常检测的应用。SVGD(Stein Variational Gradient Descent)是一种通用的变分推断算法,它是优化中梯度下降的自然对应物。SVGD通过应用一种功能性梯度下降来迭代地传输一组粒子,以最小化KL散度,从而与目标分布相匹配。
文章目录
- 一、AnoSVGD算法介绍
- AnoSVGD算法的数学原理
- AnoSVGD算法在处理高维数据时的计算复杂度降低策略
- 二、AnoSVGD算法的优势与不足
- AnoSVGD算法的优势
- AnoSVGD算法的不足
- 与其他异常检测方法的比较
- 二、AnoSVGD算法的应用
- AnoSVGD应用步骤
- AnoSVGD算法在异常检测中阈值的确定
- AnoSVGD算法与其他异常检测方法相比
- AnoSVGD算法模型搭建
一、AnoSVGD算法介绍
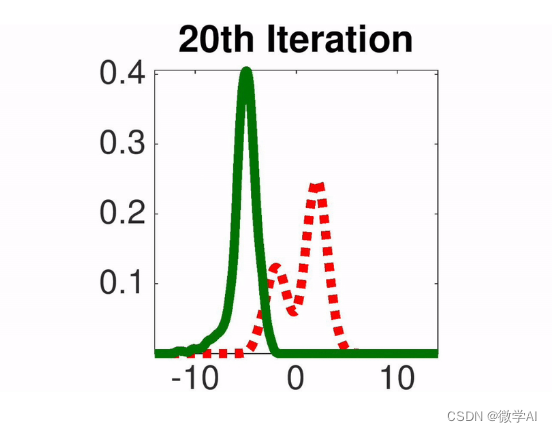
AnoSVGD是一种用于异常检测的非参数贝叶斯方法。它通过映射变换,使用已知数据的概率密度函数(PDF),多次迭代估计未知数据的概率密度函数(PDF)。在每次迭代中,基于前一次的结果,加上一个小的步长和下降方向,通过梯度下降找到最快的下降方向,从而进行迭代。这样,模型能够快速地找到未知数据的分布,并在达到目标后停止迭代。
AnoSVGD算法的数学原理
AnoSVGD(Anomaly Detection using Stein Variational Gradient Descent)是一种基于Stein变分梯度下降的非参数贝叶斯方法,用于异常检测。这种方法通过Stein变分梯度下降来近似数据生成分布,进而识别出那些与正常数据分布不一致的异常点。
AnoSVGD的基本数学原理和公式过程如下:
- Stein变分梯度下降(SVGD):
SVGD是一种用于生成似然分布样本的优化方法。它通过迭代更新一组粒子,使得这些粒子逐渐逼近目标分布。对于给定的目标分布 p ( x ) p(x) p(x),SVGD更新粒子的方式是:
x t + 1 ← x t + ϵ ϕ ( x t ) x_{t+1} \leftarrow x_t + \epsilon \phi(x_t) xt+1←xt+ϵϕ(xt)
其中, ϕ ( x t ) \phi(x_t) ϕ(xt)是Stein算子, ϵ \epsilon ϵ是学习率。 - Stein算子:
Stein算子用于度量两个分布之间的差异。对于两个分布 p ( x ) p(x) p(x)和 q ( x ) q(x) q(x),Stein算子定义为:
f ( x ) = δ q ( x ) δ x + q ( x ) ∇ x log p ( x ) f(x) = \frac{\delta q(x)}{\delta x} + q(x) \nabla_x \log p(x) f(x)=δxδq(x)+q(x)∇xlogp(x)
在AnoSVGD中, q ( x ) q(x) q(x)通常是一个简单的先验分布,如高斯分布,而 p ( x ) p(x) p(x)是数据生成分布。 - 异常检测:
在异常检测的上下文中,AnoSVGD首先使用SVGD来近似数据生成分布 p ( x ) p(x) p(x)。然后,它计算每个数据点的Stein差异,将那些具有高Stein差异的点标记为异常。 - Stein差异:
对于一个数据点 x x x,其Stein差异可以通过计算Stein算子 f ( x ) f(x) f(x)的范数来估计:
S ( x ) = ∥ f ( x ) ∥ 2 S(x) = \lVert f(x) \rVert^2 S(x)=∥f(x)∥2
大的Stein差异意味着数据点 x x x与近似的数据生成分布差异较大,因此可能是异常点。
AnoSVGD通过Stein变分梯度下降来近似数据生成分布,并使用Stein差异来识别异常点。这种方法特别适用于高维数据和复杂的数据分布。
AnoSVGD算法在处理高维数据时的计算复杂度降低策略
AnoSVGD它通过适应性地调整步长和方向来优化目标函数。在处理高维数据时,AnoSVGD面临的主要挑战是计算成本的显著增加,因为高维数据的梯度计算和Hessian矩阵的逆计算都非常耗时。为了解决这一问题,AnoSVGD采用了以下几种策略来减少计算复杂度:
-
子采样策略:AnoSVGD通过从整个数据集中随机选择一小部分样本(迷你批次)来估计梯度,这样可以大大减少每次迭代所需的计算量。
-
自适应学习率:AnoSVGD采用自适应学习率策略,根据当前的优化状态动态调整步长,避免在高维空间中过度搜索,从而减少不必要的计算。
-
近似方法:在计算梯度和Hessian矩阵时,AnoSVGD可能会采用近似方法,如随机近似高斯积分,以进一步减少计算负担。
-
稀疏化技术:对于具有大量零元素或接近零元素的高维数据,AnoSVGD可以利用稀疏矩阵的特性来减少计算和存储开销。
-
分布式计算:在处理大规模高维数据集时,AnoSVGD可以利用分布式计算资源,将数据和计算任务分配到多个处理器或服务器上进行,从而加速优化过程。
AnoSVGD能够有效地处理高维数据,同时保持较高的计算效率,这对于现代机器学习和深度学习中的大规模数据分析尤为重要。
二、AnoSVGD算法的优势与不足
AnoSVGD算法的优势
AnoSVGD算法是一种基于变分推断的异常检测方法,它通过映射变换,用已知数据的概率密度函数(PDF),多次迭代估计未知数据的概率密度函数(PDF)。这种方法的优势在于能够快速地找到未知数据的分布,并在达到目标后停止迭代,从而实现高效的异常检测。
AnoSVGD算法的不足
尽管AnoSVGD算法在某些方面表现出色,但它也可能存在一些不足。例如,它可能对数据的分布假设较为严格,对于高维数据或噪声数据可能不够鲁棒。此外,AnoSVGD算法的性能可能受到数据集特性的影响,例如数据的多样性和复杂性。
与其他异常检测方法的比较
与其他异常检测方法相比,AnoSVGD算法在处理复杂数据集时可能具有一定的优势,因为它能够通过迭代估计来捕捉数据的概率密度函数。然而,对于简单数据集或噪声较少的数据集,其他方法如基于统计的方法或基于距离的方法可能更为适用。在实际应用中,选择哪种异常检测方法取决于具体的数据特性和应用场景。
二、AnoSVGD算法的应用
AnoSVGD应用步骤
-
数据准备:首先,收集正常数据集,并对其进行预处理,包括数据清洗、规范化和特征提取。
-
模型初始化:选择一个合适的概率模型作为异常检测模型的起点,例如高斯混合模型(Gaussian Mixture Model, GMM)。
-
变分推断:使用变分推断来近似后验概率分布,这通常涉及到最大化一个下界(ELBO)。
-
梯度下降:利用梯度下降来优化模型参数,使ELBO最大化。在这个过程中,可以使用蒙特卡洛方法来近似梯度。
-
异常检测:使用优化后的模型来计算新数据的异常得分,得分高于某个阈值的数据被标记为异常。
-
模型更新:根据新数据的反馈,更新模型参数,以更好地适应正常数据的分布。
-
迭代优化:重复步骤3至6,直到模型收敛或达到预设的迭代次数。
-
结果评估:使用测试集评估模型的异常检测性能,包括准确率、召回率和F1分数等指标。
AnoSVGD算法在异常检测中阈值的确定
在异常检测中,确定阈值是一个关键步骤,因为它决定了什么水平的数据被认为是异常的。对于AnoSVGD(Anomaly Detection via Stochastic Variational Gradient Descent)算法,阈值的确定通常涉及到以下几个方面:
-
模型训练和验证:在训练阶段,AnoSVGD算法会学习数据的概率密度函数。在验证阶段,模型会对验证集进行预测,并根据预测结果来确定阈值。
-
异常分数的计算:AnoSVGD算法会计算每个数据点的异常分数,这个分数反映了数据点相对于正常数据分布的异常程度。
-
阈值的选择:阈值的确定可以基于多种策略,例如:
- 固定阈值:选择一个固定的阈值,所有高于这个阈值的数据点都被认为是异常的。
- 动态阈值:根据数据的历史行为或当前行为动态调整的阈值,这种方法相较于固定阈值更为灵活,能够更好地适应数据的动态变化。
- 统计方法:例如,可以计算数据的平均值和标准差,然后设定一个阈值范围,将超出这个范围的点视为异常。或者,可以使用中位数和IQR(四分位距)来设定阈值范围。
-
实验和调优:在实际应用中,可能需要通过实验来调整阈值,以达到最佳的检测效果。这可能涉及到尝试不同的阈值设置,并评估其对检测性能的影响。
AnoSVGD算法在异常检测中确定阈值的方法可能包括模型训练和验证、异常分数的计算、阈值的选择以及实验和调优等步骤。具体的阈值确定方法可能会根据数据的特性和业务需求有所不同。
AnoSVGD算法与其他异常检测方法相比
与其他异常检测方法相比,AnoSVGD算法在处理复杂数据分布和实时检测方面具有优势。例如,与基于统计的方法相比,AnoSVGD不受数据分布假设的限制,能够更好地捕捉数据的内在结构。与基于机器学习的方法相比,AnoSVGD作为一种非参数方法,不需要大量标注数据,适用于数据标签稀缺的场景。然而,与基于深度学习的方法相比,AnoSVGD可能在处理高度非线性数据时略显不足,因为深度学习模型能够学习数据的高级特征。
AnoSVGD算法在异常检测领域具有独特的优势,但也面临一些挑战。在选择使用AnoSVGD算法时,需要根据具体的应用场景和数据特性进行权衡。
AnoSVGD算法模型搭建
import numpy as np
from scipy.spatial.distance import pdist, squareform
class SVGD():
def __init__(self):
pass
def svgd_kernel(self, theta, h = -1):
sq_dist = pdist(theta)
pairwise_dists = squareform(sq_dist)**2
if h < 0: # if h < 0, using median trick
h = np.median(pairwise_dists)
h = np.sqrt(0.5 * h / np.log(theta.shape[0]+1))
# compute the rbf kernel
Kxy = np.exp( -pairwise_dists / h**2 / 2)
dxkxy = -np.matmul(Kxy, theta)
sumkxy = np.sum(Kxy, axis=1)
for i in range(theta.shape[1]):
dxkxy[:, i] = dxkxy[:,i] + np.multiply(theta[:,i],sumkxy)
dxkxy = dxkxy / (h**2)
return (Kxy, dxkxy)
def update(self, x0, lnprob, n_iter = 1000, stepsize = 1e-3, bandwidth = -1, alpha = 0.9, debug = False):
# Check input
if x0 is None or lnprob is None:
raise ValueError('x0 or lnprob cannot be None!')
theta = np.copy(x0)
# adagrad with momentum
fudge_factor = 1e-6
historical_grad = 0
for iter in range(n_iter):
if debug and (iter+1) % 1000 == 0:
print('iter ' + str(iter+1) )
lnpgrad = lnprob(theta)
# calculating the kernel matrix
kxy, dxkxy = self.svgd_kernel(theta, h = -1)
grad_theta = (np.matmul(kxy, lnpgrad) + dxkxy) / x0.shape[0]
# adagrad
if iter == 0:
historical_grad = historical_grad + grad_theta ** 2
else:
historical_grad = alpha * historical_grad + (1 - alpha) * (grad_theta ** 2)
adj_grad = np.divide(grad_theta, fudge_factor+np.sqrt(historical_grad))
theta = theta + stepsize * adj_grad
return theta
AnoSVGD算法在工业领域的应用案例中,一个值得关注的例子是蚂蚁集团在异常检测和归因诊断方面的实践。在蚂蚁集团,AnoSVGD算法被用于构建一个能够实时处理大量指标数据的系统,该系统支持全生命周期的监控,并能够毫秒级地处理,满足业务性能要求。AnoSVGD算法通过映射变换,使用已知数据的概率密度函数(PDF),多次迭代估计未知数据的概率密度函数(PDF),从而有效地表征未知数据的分布,并在达到目标后停止迭代。