多益网络
近日,多益网络官方微博发帖,公然表示对法院仲裁结果不服,认为劳动法有极多问题。

大家不要看微博内容似乎振振有词,极有可能只是多益网络单方面的选择性表达,毕竟多益网络的臭名早就家喻户晓。
况且对前员工直接实名指出,这操作也是第一次见。
不知道大家对多益网络认识有多少,对多益网络的创始人徐波,认识又有多少。
帮大家回忆一下那些奇葩新闻,大家可能就有印象了。
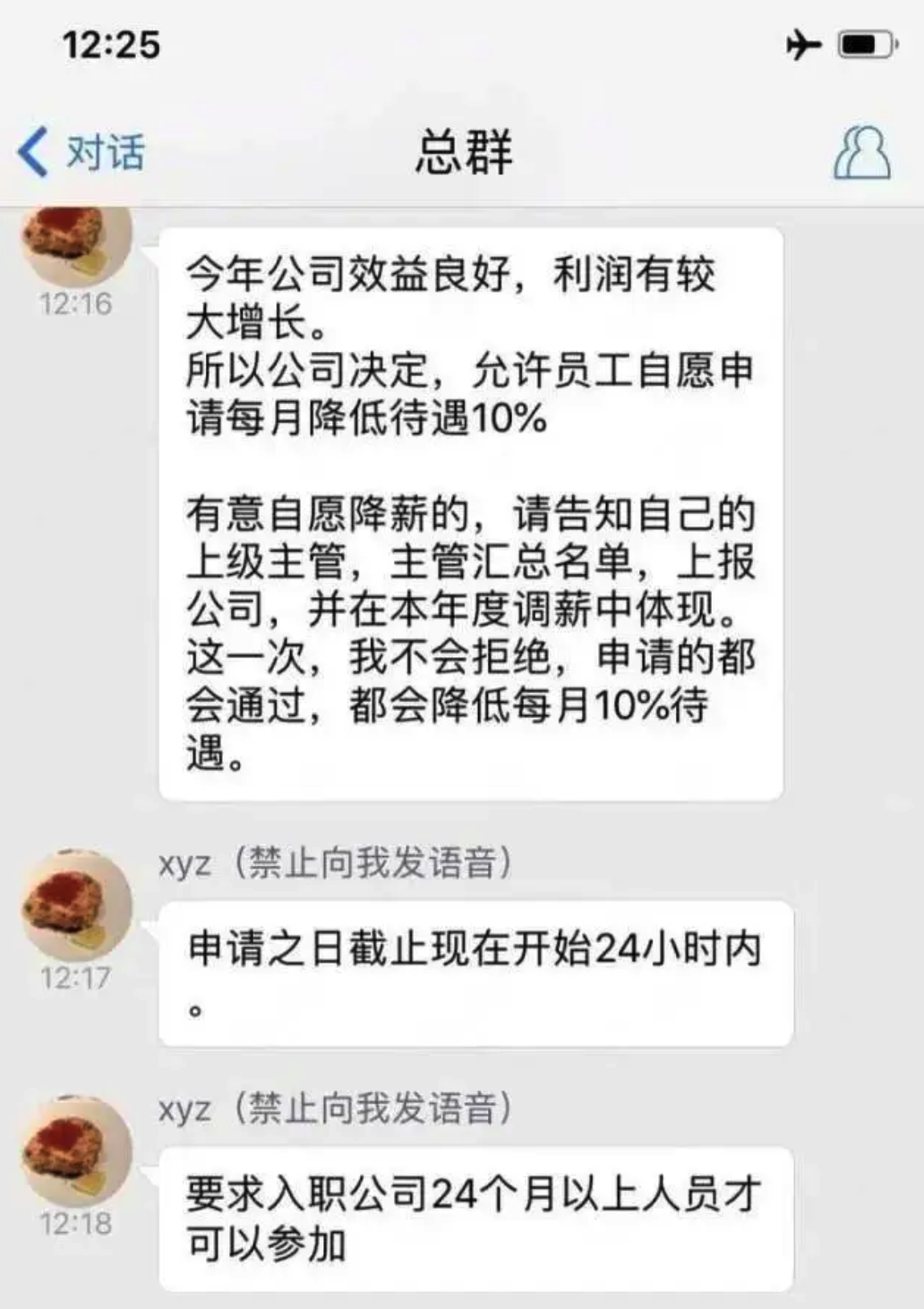
著名的"自愿降薪"事件:今年公司效益良好,利润有较大增长。公司决定,允许员工自愿申请每月降低待遇的 10%。
和"自愿降薪"类似的事情还有"要红包"事件:入职满一年及以上的员工可向徐波发感谢红包。
虽然这些"降薪"和"要红包"操作,后来都变成了"涨薪"和"发红包"。
但奖赏员工的公司多了去了,这么搞"钓鱼"操作,每年都玩「服从性/忠诚度测试」的公司,多益网络是独一家。
很难想象,一家公司的奖励机制,不是依靠于员工贡献,而是依靠于员工是否了解老板脾性,是否愿意"配合"老板玩服从性测试小游戏。
除此以外,多益网络还有规定员工娶妻彩礼不能超过 10 万元,否则就通报批评。
除了在公司里的这些奇葩操作,多益网络创始人徐波的私下生活也一度成为网友口中的 🍉。
徐波在多年前就表示:不会结婚,并且要生许多孩子。于是长期让其女友给自己介绍其他女生 🤮,并表示自己和女友之间绝对信任,最终被该女友骗走 3 个亿。
现在再看文章开头的微博原文,你还会觉得多益网络和员工之间的纠纷,会是这么简单吗?
...
回归主题。
来一道「多益网络」无关,但做多确实有益的算法题。
题目描述
平台:LeetCode
题号:1217
有 n 个筹码。第
个筹码的位置是 position[i]。
我们需要把所有筹码移到同一个位置。在一步中,我们可以将第 个筹码的位置从 改变为:
-
position[i] + 2 或 position[i] - 2,此时cost = 0 -
position[i] + 1 或 position[i] - 1,此时cost = 1
返回将所有筹码移动到同一位置上所需要的 最小代价 。
示例 1: 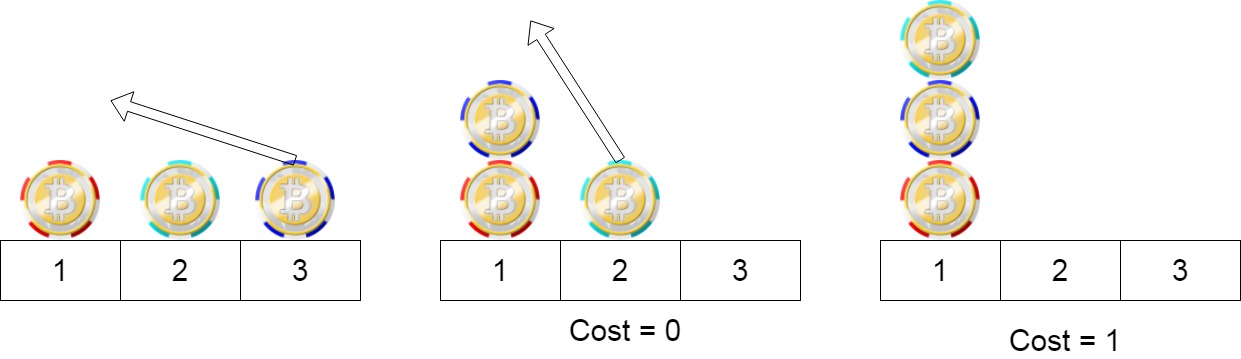
输入:position = [1,2,3]
输出:1
解释:第一步:将位置3的筹码移动到位置1,成本为0。
第二步:将位置2的筹码移动到位置1,成本= 1。
总成本是1。
示例 2: 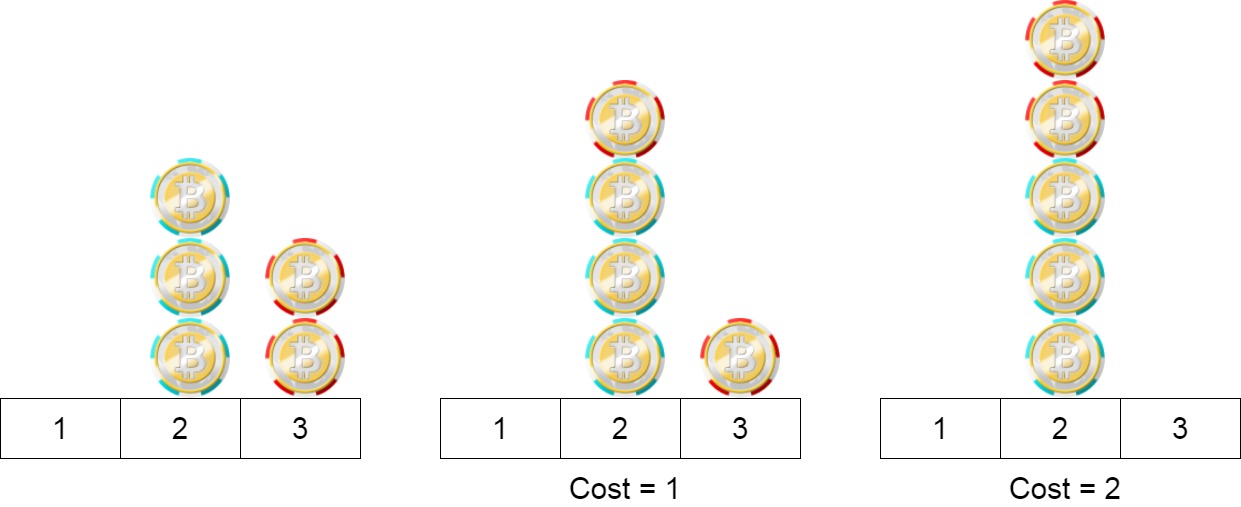
输入:position = [2,2,2,3,3]
输出:2
解释:我们可以把位置3的两个筹码移到位置2。每一步的成本为1。总成本= 2。
示例 3:
输入:position = [1,1000000000]
输出:1
提示:
贪心 + 枚举目标位置
假设移动的目标位置是 a,当前所在位置是 b,将小球从 b 移动到 a 的成本取决于两位置距离的「奇偶性」,距离为偶数时成本固定为 0,距离为奇数时成本固定为 1。
同时我们可以通过「分情况讨论」来证明,所有小球移动到一个全新位置(起始没有小球的位置),结果不会变好,假设所选择的最终(全新)位置为 t:
-
假设选择的位置 导致所有数到位置 距离均为偶数,此时总成本为 ,同时可知所有数的位置奇偶性相同,此时选择所有数中的任意一个的位置,同样可得总成本为 的结果,因此选全新的位置不会让结果变好; -
假设选择的位置 导致所有数到位置 距离均为奇数,此时总成本为 ,同时可知所有数的位置奇偶性相同,此时选择所有数中的任意一个的位置,可得总成本为 的结果,因此选全新的位置会让结果变差; -
假设选择的位置 导致所有数到位置 距离奇数结果为 ,偶数结果为 ,可知 ,同时我们通过调整 的奇偶性来确保 。此时总的成本为 ,同时可知所有与 距离为奇数的数所在位置奇偶性相同,所有与 距离为偶数的数所在位置奇偶性也相同,此时将 调整为与 奇偶性相同的原有数的位置,同样能够得到总成本为 的结果,因此选全新的位置不会让结果变好。
综上,我们可以枚举所有已有的位置为目标位置,并通过奇偶性统计其余位置到目标位置的成本,在所有已有位置中取最小的总成本即是答案。
Java 代码:
class Solution {
public int minCostToMoveChips(int[] ps) {
int n = ps.length, ans = Integer.MAX_VALUE;
for (int i = 0; i < n; i++) {
int a = ps[i], cur = 0;
for (int j = 0; j < n; j++) {
int b = ps[j];
cur += Math.abs(a - b) % 2;
}
ans = Math.min(ans, cur);
}
return ans;
}
}
C++ 代码:
class Solution {
public:
int minCostToMoveChips(vector<int>& ps) {
int n = ps.size(), ans = numeric_limits<int>::max();
for (int i = 0; i < n; i++) {
int a = ps[i], cur = 0;
for (int j = 0; j < n; j++) {
int b = ps[j];
cur += abs(a - b) % 2;
}
ans = min(ans, cur);
}
return ans;
}
};
Python 代码:
class Solution:
def minCostToMoveChips(self, ps: List[int]) -> int:
n, ans = len(ps), float('inf')
for i in range(n):
a, cur = ps[i], 0
for j in range(n):
b = ps[j]
cur += abs(a - b) % 2
ans = min(ans, cur)
return ans
TypeScript 代码:
function minCostToMoveChips(ps: number[]): number {
let n = ps.length, ans = 0x3f3f3f3f;
for (let i = 0; i < n; i++) {
let a = ps[i], cur = 0;
for (let j = 0; j < n; j++) {
const b = ps[j];
cur += Math.abs(a - b) % 2;
}
ans = Math.min(ans, cur);
}
return ans;
};
-
时间复杂度: -
空间复杂度:
贪心 + 统计奇偶性
更进一步,我们可以发现要使得「总的移动成本最优」的目标位置有无数个,只要目标位置的奇偶性不变,即可确保总成本不变。
因此我们可以省去枚举具体位置的操作,转而统计原有数的奇偶位置个数,假设偶数位置有 a 个,奇数位置有 b 个,最终目标位置选为偶数的成本为 b,最终目标位置选为奇数的成本为 a,即两者中的最小值即是答案。
Java 代码:
class Solution {
public int minCostToMoveChips(int[] ps) {
int n = ps.length, a = 0;
for (int i : ps) a += i % 2;
return Math.min(a, n - a);
}
}
C++ 代码:
class Solution {
public:
int minCostToMoveChips(vector<int>& ps) {
int n = ps.size(), a = 0;
for (int i : ps) a += i % 2;
return min(a, n - a);
}
};
Python 代码:
class Solution:
def minCostToMoveChips(self, ps: List[int]) -> int:
n, a = len(ps), sum(x % 2 for x in ps)
return min(a, n - a)
TypeScript 代码:
function minCostToMoveChips(ps: number[]): number {
const n = ps.length;
let a = ps.filter(x => x % 2 === 1).length;
return Math.min(a, n - a);
};
-
时间复杂度: -
空间复杂度:
最后
巨划算的 LeetCode 会员优惠通道目前仍可用 ~
使用福利优惠通道 leetcode.cn/premium/?promoChannel=acoier,年度会员 有效期额外增加两个月,季度会员 有效期额外增加两周,更有超大额专属 🧧 和实物 🎁 福利每月发放。
我是宫水三叶,每天都会分享算法知识,并和大家聊聊近期的所见所闻。
欢迎关注,明天见。