文章目录
- 一、前言
- 二、问题
- 问题:1326. 需要安排几位师傅加工零件
- 问题:1228. 排队打水问题
- 问题:1229. 拦截导弹的系统数量求解
- 三、感谢
一、前言
本章节主要对贪心问题进行讲解,包括《1326. 需要安排几位师傅加工零件》《1228. 排队打水问题》《1229. 拦截导弹的系统数量求解》题目。
二、问题
问题:1326. 需要安排几位师傅加工零件
类型:贪心
题目描述:
某工厂有 n 个零件加工的师傅,每位师傅每天能够加工出不同数量的零件。
现有 m 个零件要求一天加工完,请问该工厂最少需要派几个师傅来完成这次零件加工任务,如果安排所有的师傅都参与加工也不能在一天内完成任务,请输出NO。
输入:
第一行有两个整数,用空格隔开;
第一个整数代表要加工的总零件个数 m (m≤10^6),第二个整数代表工厂的零件加工师傅的数量 n(n≤100)。
第二行有 n 个整数,分别代表每个师傅每天能够加工出来的零件数量(每个师傅每天加工的零件数量≤10^4)。
输出:
输出工厂在 1 天时间内加工所有零件需要的师傅数量,或者输出NO。
样例:
输入:
10 5
1 3 2 4 2
输出:
4

1.分析问题
- 已知:总零件个数m,加工师傅的数量n,每个师傅每天能够加工出来的零件数量;
- 未知:该工厂最少需要派几个师傅来完成这次零件加工任务,如果安排所有的师傅都参与加工也不能在一天内完成任务,请输出NO。
- 关系:贪心。
2.定义变量
//二、数据定义
int m,n,a[110],s=0;
3.输入数据
//三、数据输入
cin>>m>>n;
for(int i=0;i<n;i++){
cin>>a[i];
}
4.数据计算
- 自定义比较函数,用于降序排序。
bool cmp(int a1,int a2){
if(a1>a2){
return true;
}else{
return false;
}
}
- 使用sort函数配合自定义的比较函数cmp对师傅的能力进行降序排序。
- 接下来,遍历排序后的师傅列表,累加他们的日加工能力直到达到或超过总需求量m。
- 一旦满足条件,立即输出师傅数量并跳出循环。
//四、数据计算
sort(a,a+n,cmp);
for(int i=0;i<n;i++){
s+=a[i];
if(s>=m){
cout<<i+1;
break;
}
}
5.输出结果
- 如果循环结束后累加的能力值s仍小于m,说明即使所有师傅都参与也不能一天完成任务,于是输出"NO"。
//五、输出结果
if(s<m){
cout<<"NO";
}
return 0;
完整代码如下:
#include<bits/stdc++.h> // 包含常用的C++库函数和数据结构
using namespace std; // 使用标准命名空间std,避免std::的前缀
// 自定义比较函数,用于降序排序
bool cmp(int a1, int a2) {
if (a1 > a2) { // 如果a1大于a2
return true; // 返回true,表示a1应排在a2前面
} else {
return false; // 否则返回false
}
}
int main() {
// 一、问题分析
// 给定总零件数m,师傅数量n,及每个师傅的日加工能力,确定最少需要几位师傅完成任务,若不能一天完成则输出NO。
// 二、数据定义
int m, n, a[110], s = 0; // m: 总零件数, n: 师傅数量, a[]: 存储每个师傅的日加工能力, s: 当前累加的加工能力
// 三、数据输入
cin >> m >> n; // 输入总零件数m和师傅数量n
for (int i = 0; i < n; i++) {
cin >> a[i]; // 输入每个师傅的日加工能力
}
// 四、数据处理与计算
sort(a, a + n, cmp); // 将师傅按日加工能力降序排序
for (int i = 0; i < n; i++) {
s += a[i]; // 累加当前师傅的加工能力到s
if (s >= m) { // 如果累加的加工能力达到或超过了总需求
cout << i + 1; // 输出当前已考虑的师傅数量(由于i从0开始,实际人数为i+1)
break; // 达到条件,退出循环
}
}
// 五、输出结果
if (s < m) { // 如果累加的加工能力仍然小于总需求
cout << "NO"; // 输出NO,表示无法在一天内完成任务
}
return 0; // 程序执行完毕,正常退出
}
问题:1228. 排队打水问题
类型:贪心
题目描述:
有 n 个人排队到r 个水龙头去打水,他们装满水桶的时间 t1,t2,…,tn 为整数且各不相等,应如何安排他们的打水顺序才能使他们花费的总时间最少?
每个人打水的时间 = 排队的时间 + 实际打水的时间,本题假设一个人打好水,排在他后面的人接着打水的这个切换过程不消耗时间。
比如,有 2 个人 A 和 B ,他们打水的时间分别是 3 和 2 ,只有 1 个水龙头,这时,如果 A 先打水,B 后打水,那么 A 和 B 打水的时间分别为 3 、3+2( B 排队 3 分钟)。
因此,所有人打水的总时间就是每个人的打水时间及每个人的排队时间的总和。
输入:
第 1 行,两个整数n (1≤n≤500) 和 r (1≤r≤100)。
第 2 行,n 个正整数 t1,t2,…,tn ,(1≤ti≤1000)表示每个人装满水桶的时间。
输出:
1 行,一个正整数,表示他们花费的最少总时间。
样例:
输入:
4 2
2 6 4 5
输出:
23

1.分析问题
- 已知: n个人,r个水龙头,每个人装满水桶的时间;
- 未知:花费的最少总时间;
- 关系:贪心。
2.定义变量
- n: 人数。
- r: 水龙头数量。
- t[110]: 存储每个人装满水桶所需时间的数组。
- s_time: 初始化最少总时间为0。
- x: 临时变量,用于循环计算过程中的索引调整。
//二、数据定义
int n,r,t[110],s_time=0,x;
3.输入数据
- 读取人数 n 和水龙头数量 r。
- 遍历输入每个人装水所需时间 t[i]。
//三、数据输入
cin>>n>>r;
for(int i=0;i<n;i++){
cin>>t[i];
}
4.数据计算
- 使用 sort() 函数对时间数组 t[] 进行升序排序,确保先处理耗时短的人。
- 遍历排序后的时间数组,前 r 个人直接累加他们的时间到 s_time,因为此时每个水龙头都能立即被使用。
- 当超过 r 个人后,通过变量 x 回溯,每次回退 r 个位置并累加时间,模拟新一组人开始使用水龙头的过程。这样可以保证总是最短时间的人在有机会时优先使用水龙头
//四、数据计算
sort(t,t+n);
for(int i=0;i<n;i++){
if (i<r){
s_time+=t[i];
}else{
x=i;
while(x>=0){
s_time+=t[x];
x-=r;
}
}
}
5.输出结果
- 输出最少总时间 s_time。
//五、输出结果
cout<<s_time;
return 0;
完整代码如下:
#include<bits/stdc++.h> // 引入标准库,包含常用的数据结构和算法
using namespace std; // 使用std命名空间,简化代码中的std::调用
int main(){ // 主函数开始
// 一、问题分析
// 已知:n个人需要用水龙头装满自己的水桶,总共有r个水龙头可用,
// 每个人装满水桶所需时间不同(t[i])。目标是找到一种分配方案,
// 使得所有人装满水桶的总时间最短。
// 二、数据定义
int n, r; // n: 人数, r: 水龙头数量
int t[110]; // t[i]: 第i个人装满水桶所需的时间
int s_time = 0; // s_time: 计算总的最短时间
int x; // 辅助变量,用于计算累计时间时的索引调整
// 三、数据输入
cin >> n >> r; // 输入人数n和水龙头数量r
for(int i = 0; i < n; i++){
cin >> t[i]; // 输入每个人装满水桶所需的时间
}
// 四、数据计算
// 首先对时间进行升序排序,使得时间短的人优先使用水龙头
sort(t, t + n);
// 遍历排序后的时间数组
for(int i = 0; i < n; i++){
// 前r个人直接累加他们的时间到总时间,因为此时每个水龙头都有人使用
if (i < r){
s_time += t[i];
}else{
// 当超过r个人后,每隔r个人的时间累加一次到总时间
// 这样做是为了模拟新一波人开始使用水龙头的情况
x = i; // 从当前索引开始
while(x >= 0){
s_time += t[x]; // 累加时间
x -= r; // 跳回到可以再次累加的时间点(模拟新的一轮)
}
}
}
// 五、输出结果
cout << s_time; // 输出最少的总时间
return 0; // 程序成功执行结束
} // 主函数结束
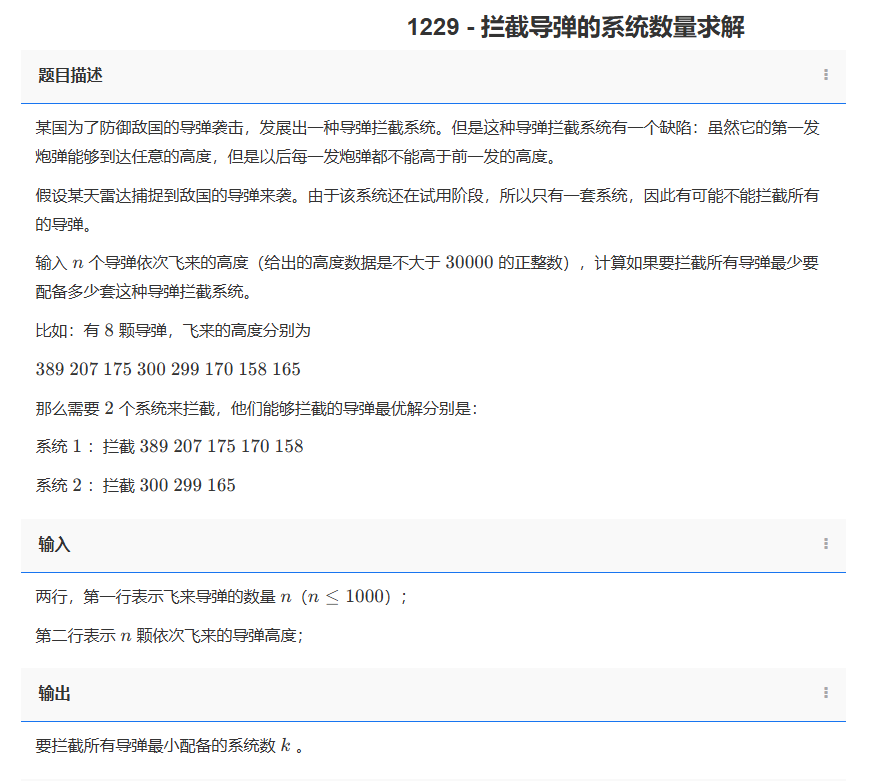
问题:1229. 拦截导弹的系统数量求解
类型:贪心
题目描述:
某国为了防御敌国的导弹袭击,发展出一种导弹拦截系统。但是这种导弹拦截系统有一个缺陷:虽然它的第一发炮弹能够到达任意的高度,但是以后每一发炮弹都不能高于前一发的高度。
假设某天雷达捕捉到敌国的导弹来袭。由于该系统还在试用阶段,所以只有一套系统,因此有可能不能拦截所有的导弹。
输入 n 个导弹依次飞来的高度(给出的高度数据是不大于 30000 的正整数),计算如果要拦截所有导弹最少要配备多少套这种导弹拦截系统。
比如:有 8 颗导弹,飞来的高度分别为
389 207 175 300 299 170 158 165
那么需要 2 个系统来拦截,他们能够拦截的导弹最优解分别是:
系统 1 :拦截 389 207 175 170 158
系统 2 :拦截 300 299 165
输入:
两行,第一行表示飞来导弹的数量 n(n≤1000);
第二行表示 n 颗依次飞来的导弹高度;
输出:
要拦截所有导弹最小配备的系统数 k 。
样例:
输入:
8
389 207 175 300 299 170 158 165
输出:
2
1.分析问题
- 已知:n 枚导弹依序列飞行并报告其高度;
- 未知:确定拦截所有导弹最少需要配置的导弹拦截系统数量;
- 关系:每个拦截系统的首枚导弹能到达任意高度,但后续导弹不得高于前一枚。
2.定义变量
- n: 导弹数量, a[]: 存储导弹高度, c: 系统计数器, s: 当前系统处理导弹的累加高度, temp: 记录局部最小高度。
- isFind: 标志是否已找到所有导弹的处理方案
// 数据定义
int n, a[1010] = {}, c = 0, s = 0, temp = INT_MAX;
bool isFind = false;
3.输入数据
- 读取每个导弹的飞行高度
// 数据输入
cin >> n;
for(int i = 0; i < n; i++) {
cin >> a[i];
}
4.数据计算
- 累加所有非零高度的值s,创建了一种机制来判断是否所有导弹都已被至少一个系统“覆盖”;
- 通过比较,将符合条件的导弹高度设为0;
- 当s不为0时,表明仍有导弹没有处理,需要增加系统;
- 当s变为0时,表明所有导弹被标记为已处理(高度设为0)。
while(!isFind) {
temp = INT_MAX; // 初始化局部最小高度为极大值,象征“任意高度”
// 遍历导弹高度,模拟每个系统处理导弹的过程
for(int i = 0; i < n; i++) {
if(a[i] == 0) continue; // 跳过已处理(高度设为0)的导弹
s += a[i]; // 累加当前系统处理的导弹高度总和
// 更新局部最小高度,并标记该导弹为已处理
if(temp > a[i]) {
temp = a[i]; // 找到新的局部最小高度
a[i] = 0; // 标记当前局部最小高度对应的导弹已由当前系统处理
}
}
// 判断是否所有导弹都被考虑(通过累加和s)
if(s == 0) {
isFind = true; // 所有导弹均被至少一个系统覆盖
} else {
++c; // 需要新的系统来处理剩余未被标记的导弹
s = 0; // 重置累加和,准备下一轮迭代
}
}
5.输出结果
- 最少需要的导弹拦截系统数量。
// 输出结果
cout << c;
完整代码如下:
#include<bits/stdc++.h>
using namespace std;
int main(){
// 问题分析
// 已知:n 枚导弹依序列飞行并报告其高度;
// 目标:确定拦截所有导弹最少需要配置的导弹拦截系统数量;
// 特殊规则:每个拦截系统的首枚导弹能到达任意高度,但后续导弹不得高于前一枚。
// 数据定义
int n, a[1010] = {}, c = 0, s = 0, temp = INT_MAX; // n: 导弹数量, a[]: 存储导弹高度, c: 系统计数器, s: 当前系统处理导弹的累加高度, temp: 记录局部最小高度
bool isFind = false; // 标志是否已找到所有导弹的处理方案
// 数据输入
cin >> n;
for(int i = 0; i < n; i++) {
cin >> a[i]; // 读取每个导弹的飞行高度
}
// 数据计算与系统分配
while(!isFind) {
temp = INT_MAX; // 初始化局部最小高度为极大值,象征“任意高度”
// 遍历导弹高度,模拟每个系统处理导弹的过程
for(int i = 0; i < n; i++) {
if(a[i] == 0) continue; // 跳过已处理(高度设为0)的导弹
s += a[i]; // 累加当前系统处理的导弹高度总和
// 更新局部最小高度,并标记该导弹为已处理
if(temp > a[i]) {
temp = a[i]; // 找到新的局部最小高度
a[i] = 0; // 标记当前局部最小高度对应的导弹已由当前系统处理
}
}
// 判断是否所有导弹都被考虑(通过累加和s)
if(s == 0) {
isFind = true; // 所有导弹均被至少一个系统覆盖
} else {
++c; // 需要新的系统来处理剩余未被标记的导弹
s = 0; // 重置累加和,准备下一轮迭代
}
}
// 输出结果
cout << c; // 最少需要的导弹拦截系统数量
return 0; // 程序正常结束
}
思路二:
#include <bits/stdc++.h>
using namespace std;
// 变量声明
int a[1010]; // a 数组用来存储每个拦截系统能够拦截的导弹最大高度
int n, x, p, k=0;
int main(){
// 输入导弹总数
cin >> n;
// 循环读取每个导弹的高度
for(int i = 1; i <= n; i++){
cin >> x;
// 初始化 p 为 -1,表示尚未找到合适的拦截系统
p = -1;
// 遍历已有系统(从1到k),尝试找到能够拦截当前导弹的系统
for(int j = 1; j <= k; j++){
// 如果当前系统 a[j] 的拦截高度大于等于导弹高度 x,则找到了合适的系统
if(a[j] >= x){
p = j; // 记录找到的系统索引
break; // 跳出循环
}
}
// 如果没有找到能够拦截当前导弹的系统(p 仍为 -1)
if(p == -1){
// 增加一个新的系统,即 k 自增,并将新系统的拦截高度设为当前导弹的高度
k++;
a[k] = x;
}else{ // 如果找到了能够拦截的系统
// 更新该系统能够拦截的最高高度为当前导弹的高度(可能降低,但题目允许)
a[p] = x;
}
}
// 输出最少需要的拦截系统数量
cout << k;
return 0;
}
三、感谢
如若本文对您的学习或工作有所启发和帮助,恳请您给予宝贵的支持——轻轻一点,为文章点赞;若觉得内容值得分享给更多朋友,欢迎转发扩散;若认为此篇内容具有长期参考价值,敬请收藏以便随时查阅。
每一次您的点赞、分享与收藏,都是对我持续创作和分享的热情鼓励,也是推动我不断提供更多高质量内容的动力源泉。期待我们在下一篇文章中再次相遇,共同攀登知识的高峰!


![mst[讲课留档]](https://img-blog.csdnimg.cn/direct/05a3a6e1395943c2af4c142d4d259695.png)