518. 零钱兑换 II

题目链接:518. 零钱兑换 II
文档讲解:代码随想录
状态:不会
思路:
和494.目标和类似,这题属于组合问题,当我们有一个硬币coin时,对于每个金额j,通过添加这个硬币,我们可以把凑成金额j-coin的所有方法数加到凑成金额j的方法数中。这是因为每一种凑成 j-coin 的方法,加上硬币coin,都变成了一种凑成j的方法。
注意:
- dp[j] 就是所有的dp[j - coins[i]](考虑coins[i]的情况)相加。
- 要考虑dp[0]=1
- j>=coins[i]
题解:
public int change(int amount, int[] coins) {
int[] dp = new int[amount + 1]; // 创建一个长度为 amount + 1 的数组 dp,用于存储每个金额的组合数
dp[0] = 1; // 初始化 dp[0] 为 1,因为组成金额为 0 的唯一方法是使用 0 个硬币
for (int coin : coins) { // 遍历每个硬币
// for (int j = 1; j <= amount; j++) {
// if (j >= coin) {
// dp[j] += dp[j - coin];
// }
// }
for (int j = coin; j <= amount; j++) { // 从当前硬币的面值开始遍历到目标金额
dp[j] += dp[j - coin]; // 更新 dp[j],将当前硬币加入组合中
}
}
return dp[amount]; // 返回组成目标金额的组合数
}
377. 组合总和 Ⅳ

题目链接:377. 组合总和 Ⅳ
文档讲解:代码随想录
状态:还行
思路:这题属于排列问题,需要先遍历target再遍历nums。
题解:
public int combinationSum4(int[] nums, int target) {
int[] dp = new int[target + 1];
dp[0] = 1;
for (int j = 1; j <= target; j++) {
for (int i = 0; i < nums.length; i++) {
if (j >= nums[i]) {
dp[j] += dp[j - nums[i]];
}
}
System.out.println(Arrays.toString(dp));
}
return dp[target];
}
70. 爬楼梯 (进阶)
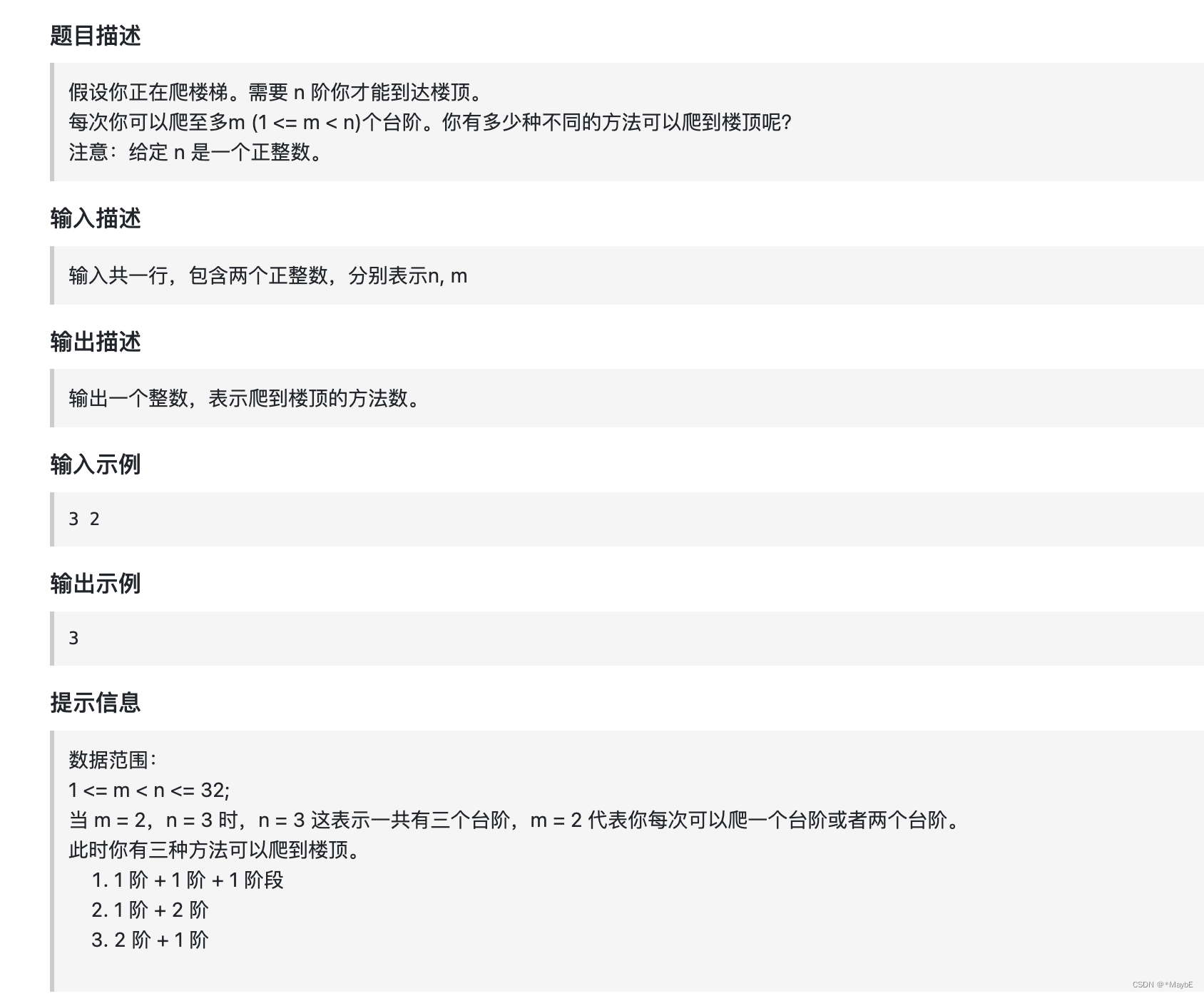
题目链接: 70. 爬楼梯 (进阶)
文档讲解:代码随想录
状态:还不熟练
思路:其实就是排列问题,但是要注意步数不能超过要爬的台阶数
题解:
public void climb() {
Scanner scanner = new Scanner(System.in);
int n = scanner.nextInt();
int m = scanner.nextInt();
int[] dp = new int[n + 1];
dp[0] = 1;
for (int i = 1; i <= n; i++) {
for (int j = 0; j <= m; j++) {
if (j <= i) {//表示步数不能超过要爬的台阶数
dp[i] += dp[i - j];
}
}
// System.out.println(Arrays.toString(dp));
}
System.out.println(dp[n]);
}