前言
标题里的EKF、UKF、CKF、PF分别为:扩展卡尔曼滤波、无迹卡尔曼滤波、容积卡尔曼滤波、粒子滤波。
EKF是扩展卡尔曼滤波,计算快,最常用于非线性状态方程或观测方程下的卡尔曼滤波。
但是EKF应对强非线性的系统时,估计效果不如UKF。
UKF是无迹卡尔曼滤波/无味卡尔曼滤波,使用UT变换产生多个sigma点,对点的预测和加权求和来模拟非线性的转移,精度较高、计算量也比较大。
但是UKF的UT变换理论依据不明确,且实际运行时容易出现矩阵奇异的情况,因此提出来CKF
CKF是容积卡尔曼滤波,容积变换理论意义更明确、运行更稳定。
PF通常使用大量的粒子来进行计算,要想达到UKF或CKF的精度,计算量往往很大,不过通过增加粒子数量也能获得更高的定位效果。
以上方法没有谁好谁不好的说法,必须结合使用场景、精度要求、滤波量的类型等因素来确定,所以这里给出以上四个方法估计同一种状态的MATLAB代码,用于对比。
程序结构
程序背景是组合导航下的卡尔曼滤波,三维状态量可以理解成三维的位置,也可以理解成三维的速度。相应的,三维的输入量可以理解成三维的速度,也可以理解成三维的加速度,比较灵活。
程序结构如下:
初始化→运动模型建立→滤波参数设置→EKF→UKF→CKF→PF→误差计算→结果绘制

程序运行结果
状态量的真值、各方法估计值对比:
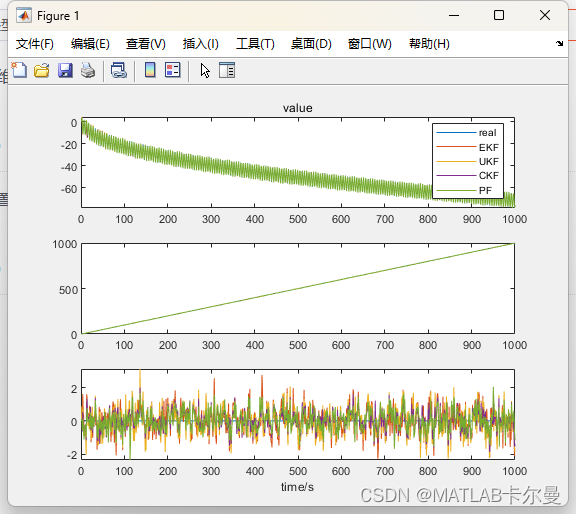
放大后得到如下图像:
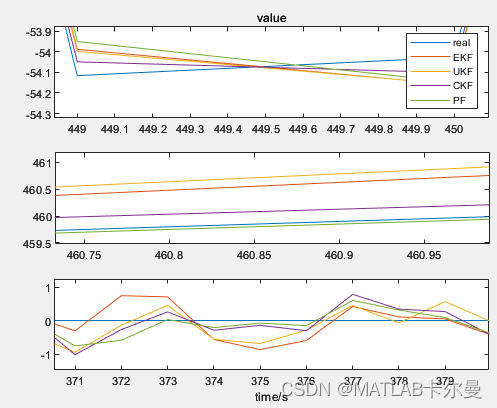
误差图像如下:
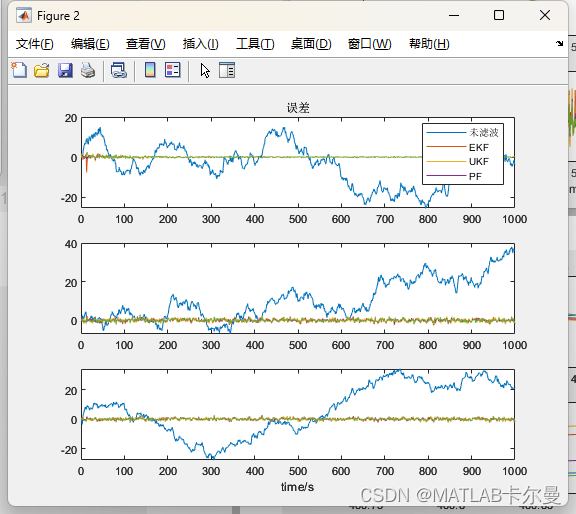
其中,“未滤波”表示纯INS计算的结果。
会自动计算当前各方法计算的误差统计特性(误差最大值、平均值),如下:

只有一个m文件,方便调试和学习。
部分代码
% EKF+UKF+CKF+PF,四个滤波效果对比
% author:Evand©2024
% date: 2024-06-29/Ver1
clear;clc;close all;
rng(0);
%% 滤波模型初始化
t = 1:1:1000;% 定义时间序列
Q = 1*diag([1,1,1]);% 过程噪声协方差矩阵和过程噪声
w = sqrt(Q)*randn(size(Q,1),length(t));
% 观测噪声协方差矩阵和观测噪声
R = 1*diag([1,1,1]);
v = sqrt(R)*randn(size(R,1),length(t));
P0 = 1*eye(3);% 初始状态估计协方差矩阵
X = zeros(3,length(t));% 初始化状态向量
% 初始化扩展卡尔曼滤波状态向量
X_ekf = zeros(3,length(t));
X_ekf(1,1) = X(1,1);
% 初始化观测值格式
Z = zeros(3,length(t));
% 定义初始观测值
Z(:,1) = [X(1,1)^2/20;X(2,1);X(3,1)] + v(:,1);
%% 运动模型
% 初始化未滤波的状态向量
X_ = zeros(3,length(t));
X_(:,1) = X(:,1);
% 运动模型迭代
for i1 = 2:length(t)
% 计算真实状态值
X(:,i1) = [X(1,i1-1) + (2.5 * X(1,i1-1) / (1 + X(1,i1-1).^2)) + 8 * cos(1.2*(i1-1));
X(2,i1-1) + 1;
X(3,i1-1)];
% 计算未滤波的状态值
X_(:,i1) = [X_(1,i1-1) + (2.5 * X_(1,i1-1) / (1 + X_(1,i1-1).^2)) + 8 * cos(1.2*(i1-1));
X_(2,i1-1) + 1;
X_(3,i1-1)] + w(:,i1-1);
% 计算观测值
Z(:,i1) = [X(1,i1).^2 / 20;X(2,i1);X(3,i1)] + v(i1);
end
%% EKF
% 初始化EKF协方差矩阵
P = P0;
fprintf('完整内容下载链接:https://gf.bilibili.com/item/detail/1105727012')
% 生成EKF过程噪声
w_ekf = sqrt(Q)*randn(size(Q,1),length(t));
% EKF迭代