前言
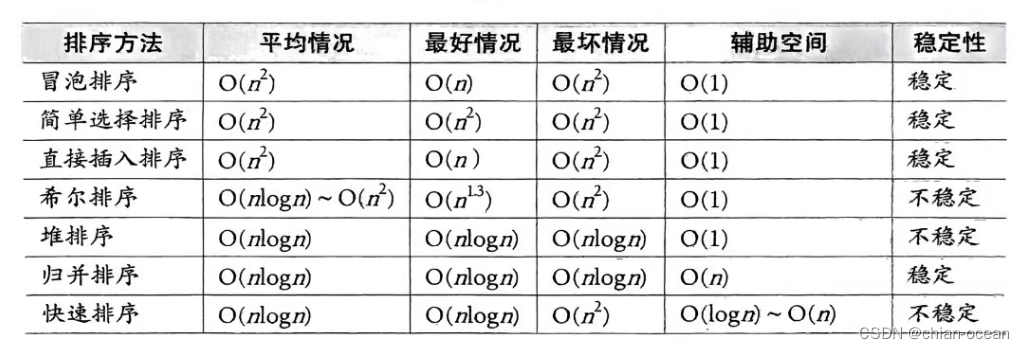
前面介绍了冒泡排序、选择排序、插入排序、希尔排序,作为排序中经常用到了算法,还有堆排序、快速排序、归并排序
堆排序(HeaSort)
堆排序的概念
堆排序是一种有效的排序算法,它利用了完全二叉树的特性。在C语言中,堆排序通常通过构建一个最大堆(或最小堆),然后逐步调整堆结构,最终实现排序。
代码实现
堆排序是一种基于二叉堆的排序算法,它通过将待排序的元素构建成一个二叉堆,然后逐步移除堆顶元素并将其放置在数组的尾部,同时维护堆的性质,直至所有元素都被排序。
注意:第一个for循环中的(n-1-1)/ 2 的含义
- 第一个减1是由n-1个元素
- 第二个减1是除以2是父亲节点。以为我们调整的是每一个根节点。(非叶子节点)
//堆排序
void HeapSort(int* a, int n)
{
//建堆
for(int i = (n - 1 - 1) / 2; i >= 0; i--)
{
AdjustDown(a,n,i);
}
//排序
int end = n - 1;
while(end > 0)
{
Swap(&a[end], &a[0]);
AdjustDown(a, end, 0);
--end;
}
}
其中AdjustDown是建立堆的函数,我们要建立一个大堆,将替换到上上面的小值,向下调整,保持大堆的结构。
代码如下:
//向下调整
void AdjustDown(int* a, int n, int parent)
{
int child = parent * 2 + 1;
while (child < n)
{
if (child + 1 < n && a[child + 1] > a[child])
{
child++;
}
if (a[parent] < a[child])
{
Swap(&a[parent], &a[child]);
parent = child;
child = parent * 2 + 1;
}
else
{
break;
}
}
}
堆排序的复杂度分析
堆排序是一种常用的排序算法,其时间复杂度通常为O(nlogn)。在C语言中实现堆排序时,时间复杂度的分析主要涉及到两个阶段:构建初始堆和进行堆排序。
- 构建初始堆:从最后一个非叶子节点开始,逐步向上调整,直到根节点满足堆的性质。这个过程的时间复杂度为
O(n),因为需要对每个非叶子节点进行一次调整。 - 进行堆排序:堆排序的过程涉及到多次交换堆顶元素和最后一个元素,并对剩余的元素进行调整。每次交换后,堆的大小减一,并对新的堆顶元素进行调整。这个过程的时间复杂度为
O(nlogn),因为每次调整的时间复杂度为O(logn),总共需要进行n-1次调整。
快速排序(Quick Sort)
快速排序的概念
快速排序(Quick Sort)是一种高效的排序算法,它的基本思想是通过一趟排序将待排记录分隔成独立的两部分,其中一部分记录的关键字均比另一部分记录的关键字小,然后再分别对这两部分记录继续进行排序,以达到整个序列有序的目的。在C语言中,快速排序的实现通常涉及到递归函数的编写,以及对数组进行分区(partition)操作。
霍尔版本(hoare)

在这里我们是要,定义一个关键字(keyi)进行分区,然后分别向左右进行递归。
代码实现
int part1(int* a, int left, int right)
{
int mid = GetmidNum(a,left,right);
Swap(&a[left], &a[mid]);
int keyi = left;
while (left < right)
{
while (left < right && a[right] >= a[keyi])
right--;
while (left < right && a[left] <=a[keyi])
left++;
Swap(&a[left], &a[right]);
}
Swap(&a[keyi], &a[left]);
keyi = left;
return keyi;
}
挖坑法
挖坑法类似于霍尔方法,挖坑就是记住关键字,保证关键字就是一个坑位,比关键字值小(大)的时候就入坑位,此时,这个值位置作为新的坑位直至两个前后指针指向同一个坑位。

代码实现
int part2(int* a, int left, int right)
{
int mid = GetmidNum(a, left, right);
Swap(&a[left], &a[mid]);
int keyi = a[left];
int hole = left;
while (left < right)
{
while (left < right && a[right] >= keyi)
right--;
Swap(&a[hole], &a[right]);
hole = right;
while (left < right && a[left] <= keyi)
left++;
Swap(&a[hole], &a[left]);
hole = left;
}
Swap(&keyi, &a[hole]);
keyi = left;
return keyi;
}
前后指针法
-
prev指针初始化为数组的开始位置,cur指针初始化为prev的下一位置。 -
cur指针向前遍历数组,寻找小于或等于基准值的元素,而prev指针则跟随cur指针的移动,直到cur找到一个小于基准值的元素。 -
一旦找到这样的元素,
prev和cur指针之间的元素都会被交换,然后cur指针继续向前移动,直到找到下一个小于基准值的元素,或者到达数组的末尾。最后,基准值会被放置在prev指针当前的位置,完成一次排序

代码实现
int part3(int* a, int left, int right)
{
int mid = GetmidNum(a, left, right);
Swap(&a[left], &a[mid]);
int keyi = left;
int cur = left + 1;
int prev = left;
while (cur <= right)
{
while (a[cur] < a[keyi] && ++prev != cur)
Swap(&a[cur], &a[prev]);
++cur;
}
Swap(&a[prev], &a[keyi]);
keyi = prev;
return keyi;
}
递归实现
以上都是递归方法,通过调用分区进行排序。
void QuickSort(int* a, int left, int right)
{
if (left >= right)
return;
int key = part3(a, left, right);
QuickSort(a, left, key - 1);
QuickSort(a, key + 1, right);
}
快速排序迭代实现(利用栈)参考:栈和队列
基本步骤
- 初始化栈:创建一个空栈,用于存储待排序子数组的起始和结束索引。
- 压栈:将整个数组的起始和结束索引作为一对入栈。
- 循环处理,在栈非空时,重复以下步骤:
- 弹出一对索引(即栈顶元素)来指定当前要处理的子数组。
- 选择子数组的一个元素作为枢轴(pivot)进行分区。
- 进行分区操作,这会将子数组划分为比枢轴小的左侧部分和比枢轴大的
代码实现
void QuickSortNonR(int* a, int left, int right)
{
ST st;
STInit(&st);
STpush(&st, left);
STpush(&st, right);
while (!STEmpty(&st))
{
int end = STTop(&st);
STPop(&st);
int begin = STTop(&st);
STPop(&st);
int keyi = part3(a, begin, end);
if (keyi + 1 < end)
{
STpush(&st, keyi + 1);
STpush(&st, end);
}
if (begin < keyi - 1)
{
STpush(&st, begin);
STpush(&st, keyi - 1);
}
}
STDestroy(&st);
}
快速排序的优化
优化角度从两个方面切入
- 在选择关键字的(基准值)时候,如果我们碰到了,有序数组,那么就会,减低排序效率。
- 方法一:三数取中,即区三个关键字先进行排序,将中间数作为关键字,一般取左端右端和中间值。
- 方法二:随机值。利用随机数生成。
三数取中代码实现
int GetmidNum(int* a, int begin, int end)
{
int mid = (begin + end) / 2;
if (a[begin] < a[mid])
{
if (a[mid] < a[end])
{
return mid;
}
else if(a[end]<a[begin])
{
return begin;
}
else
{
return end;
}
}
else //a[begin]>a[mid]
{
if (a[begin] < a[end])
{
return begin;
}
else if (a[end] < a[mid])
{
return mid;
}
else
{
return end;
}
}
随机选 key(下标) 代码实现
srand(time(0));
int randi = left + (rand() % (right - left));
Swap(&a[left], &a[randi]);
快速排序复杂度分析
- 在平均情况下,快速排序的时间复杂度为O(n log n),这是因为每次划分都能够将数组分成大致相等的两部分,从而实现高效排序。在最坏情况下,快速排序的时间复杂度为O(n^2)
- 除了递归调用的栈空间之外,不需要额外的存储空间,因此空间复杂度是O(log n)。在最坏情况下,快速排序的时间复杂度可能是 O(n),这是因为在最坏情况下,递归堆栈空间可能会增长到线性级别。
根据上述描述,优化快速排序是必要的。
归并排序(Merge Sort)

归并排序的概念
归并排序(Merge Sort)是一种基于分治策略的排序算法,它将待排序的序列分为两个或以上的子序列,对这些子序列分别进行排序,然后再将它们合并为一个有序的序列。归并排序的基本思想是将待排序的序列看作是一系列长度为1的有序序列,然后将相邻的有序序列段两两归并,形成长度为2的有序序列,以此类推,最终得到一个长度为n的有序序列。
基本操作:
- 分解:将序列每次折半划分,递归实现,直到子序列的大小为1。
- 合并:将划分后的序列段两两合并后排序。在每次合并过程中,都是对两个有序的序列段进行合并,然后排序。这两个有序序列段分别为
R[low, mid]和R[mid+1, high]。先将他们合并到一个局部的暂存数组R2中,合并完成后再将R2复制回R中。
代码实现(递归)
void _MergeSort(int* a, int* tmp, int begin, int end)
{
if (begin >= end)
return;
int mid = (begin + end) / 2;
_MergeSort(a, tmp, begin, mid - 1);
_MergeSort(a, tmp, mid + 1, end);
int begin1 = begin, end1 = mid;
int begin2 = mid + 1, end2 = end;
int i = begin;
while (begin1 <= end1 && begin2 <= end2)
{
if (a[begin1] > a[begin2])
{
tmp[i++] = a[begin2++];
}
else
{
tmp[i++] = a[begin1++];
}
}
while (begin1 <= end1)
{
tmp[i++] = a[begin1++];
}
while (begin2 <= end2)
{
tmp[i++] = a[begin2++];
}
memcpy(a + begin, tmp + begin, sizeof(int) * (end - begin + 1));
}
void MergeSort(int* a, int n)
{
int* tmp = (int*)malloc(sizeof(int) * n);
if (tmp == NULL)
{
perror("malloc fail");
return;
}
_MergeSort(a, tmp, 0, n-1);
free(tmp);
}
代码实现(迭代)
void MergeSortNonR(int* a, int n)
{
int* tmp = (int*)malloc(sizeof(int) * n);
if (tmp == NULL)
{
perror("malloc fail");
return;
}
int gap = 1;
while (gap < n)
{
for (int i = 0; i < n; i =2* gap)
{
int begin1 = i, end1 = i + gap - 1;
int begin2 = i + gap, end2 = i + 2 * gap - 1;
int j = i;
if (end1 >= n || begin2 >= n)
{
break;
}
if (end2 >= n)
{
end2 = n-1;
}
while (begin1 <= end1 && begin2 <= end2)
{
if (a[begin1] < a[begin2])
{
tmp[j++] = a[begin1++];
}
else
{
tmp[j++] = a[begin2++];
}
}
while (begin1 <= end1)
{
tmp[j++] = a[begin1++];
}
while (begin2 <= end2)
{
tmp[j++] = a[begin2++];
}
memcpy(a + i, tmp + i, sizeof(int) * (end2 - i + 1));
}
gap *= 2;
}
free(tmp);
}
归并排序复杂度分析
- 时间复杂度是 O(n log n),其中 n 是待排序元素的数量。这个时间复杂度表明,归并排序的执行速度随着输入大小的增加而线性增加,但不会超过对数级的增长。
- 空间复杂度为 O(n),在数据拷贝的时候malloc一个等大的数组。
总结
p[j++] = a[begin2++];
}
}
while (begin1 <= end1)
{
tmp[j++] = a[begin1++];
}
while (begin2 <= end2)
{
tmp[j++] = a[begin2++];
}
memcpy(a + i, tmp + i, sizeof(int) * (end2 - i + 1));
}
gap *= 2;
}
free(tmp);
}
## 归并排序复杂度分析
* 时间复杂度是 O(n log n),其中 n 是待排序元素的数量。这个时间复杂度表明,归并排序的执行速度随着输入大小的增加而线性增加,但不会超过对数级的增长。
* 空间复杂度为 O(n),在数据拷贝的时候malloc一个等大的数组。
# 总结