接雨水
42. 接雨水 - 力扣(LeetCode)
暴力解法
对计算接到的雨水,有两种方式,一是按照行来计算。

另一种是按列计算
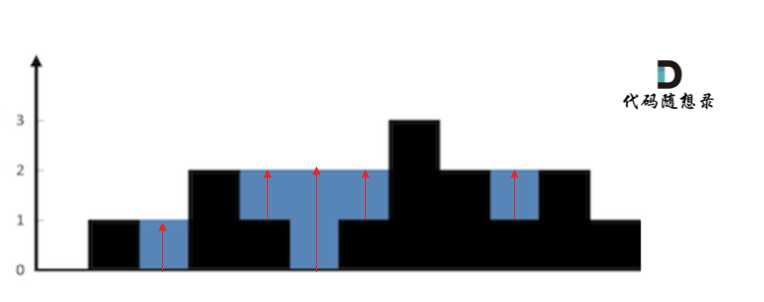
按列计算容易不乱。基本思路如下:
对每列i进行循环,在循环中,找到该列左侧的最大高度leftHeight和该列右侧的最大高度rightHeight,该列能接到的雨水为两者较小值减去该列的高度。
h = min(leftHeight,rightHeight) - height[i]
当h大于0时,将结果累加进最后的返回结果result中.
具体思路可以看代码随想录 (programmercarl.com)
代码如下
class Solution {
public:
//计算给定高度数组中能接的雨水量
int trap(vector<int>& height) {
int sum = 0; // sum 用于累计接到的雨水量
for(int i = 0; i < height.size(); i++){ // 遍历数组中的每个元素
if(i == 0 || i == height.size() - 1) // 数组的第一个和最后一个元素不能接雨水
continue; // 跳过这两个元素
int rightHeight = height[i]; // 右边最高的柱子高度,初始设为当前柱子高度
int leftHeight = height[i]; // 左边最高的柱子高度,初始设为当前柱子高度
for(int r = i + 1; r < height.size(); r++){ // 向右扫描,找到右边最高的柱子
if(height[r] > rightHeight)
rightHeight = height[r];
}
for(int l = i - 1; l >= 0; l--){ // 向左扫描,找到左边最高的柱子
if(height[l] > leftHeight)
leftHeight = height[l];
}
int h = min(leftHeight, rightHeight) - height[i]; // 计算当前位置可以接的雨水量
if(h > 0)
sum += h; // 如果可以接雨水,则加到总雨水量上
}
return sum; // 返回总的接雨水量
}
};
算法的时间复杂度为O(n^2),对于每个元素都要向左右遍历一次获取最大的leftheight和rightheight,最后2个案例会超时,ac不了,空间复杂度为O(1)。
双指针法
在上述的暴力解法中,如果我们进行调试的话,会发现每次的运行都会左右遍历一次以获取最大的leftheight和rightheight,而这有很多的计算浪费,所以我们可以在开始就从左到右,从右到左遍历一次数组,得到两个数组,分别表示每列i的leftheight和rightheight,然后用上述计算h的方法再计算一次,将算法的时间复杂度降为O(n)。
class Solution {
public:
int trap(vector<int>& height) {
int sum = 0;
vector<int> leftHeight(height.size(), 0); // 创建一个数组来存储每个位置的左边最高柱子高度
vector<int> rightHeight(height.size(), 0); // 创建一个数组来存储每个位置的右边最高柱子高度
int maxHeight_left_temp = height[0]; // 初始化左边最高柱子高度为第一个元素的高度
int maxHeight_right_temp = height[height.size() - 1]; // 初始化右边最高柱子高度为最后一个元素的高度
for (int i = 1; i < height.size(); i++) {
maxHeight_left_temp = max(maxHeight_left_temp, height[i]); // 更新左边最高柱子高度
leftHeight[i] = maxHeight_left_temp; // 存储左边最高柱子高度
}
for (int i = height.size() - 2; i >= 0; i--) {
maxHeight_right_temp = max(maxHeight_right_temp, height[i]); // 更新右边最高柱子高度
rightHeight[i] = maxHeight_right_temp; // 存储右边最高柱子高度
}
// 再次遍历数组,计算每个位置可以接的雨水量
for (int i = 0; i < height.size(); i++) {
int h = min(leftHeight[i], rightHeight[i]) - height[i]; // 计算当前位置可以接的雨水量
if (h > 0)
sum += h; // 如果可以接雨水,则加到总雨水量上
}
return sum;
}
};
算法的时间复杂度为O(n),空间复杂度为O(n)(2个长度为n的数组),以空间换时间。
单调栈法
这里想像这样一个问题,接雨水即需要找到当前柱子右侧的大于等于该柱子高度的柱子,然后计算接到的雨水,因此,可以使用单调栈法。

从左到右遍历时,需要找到比当前元素大的元素,考虑使用单调递增栈(什么问题使用什么栈参考之前day52的文章)
class Solution {
public:
int trap(vector<int>& height) {
stack<int> st; // 创建一个栈来存储柱子的索引
int sum = 0; // sum 用于累计接到的雨水量
st.push(0); // 先将第一个柱子的索引入栈
for (int i = 1; i < height.size(); i++) { // 从第二个柱子开始遍历数组
if (height[i] < height[st.top()]) { // 如果当前柱子高度小于栈顶柱子高度
st.push(i); // 将当前柱子的索引入栈
} else if (height[i] == height[st.top()]) { // 如果当前柱子高度等于栈顶柱子高度
st.pop(); // 弹出栈顶元素
st.push(i); // 将当前柱子的索引入栈
} else { // 如果当前柱子高度大于栈顶柱子高度
while (!st.empty() && height[i] > height[st.top()]) { // 当栈不为空且当前柱子高度大于栈顶柱子高度时
int mid = st.top(); // 获取栈顶柱子的索引
st.pop(); // 弹出栈顶元素
if (!st.empty()) { // 如果栈不为空
int h = min(height[st.top()], height[i]) - height[mid]; // 计算凹槽的高度
int w = i - st.top() - 1; // 计算凹槽的宽度
sum += h * w; // 计算凹槽可以接的雨水量,并加到总雨水量上
}
}
}
st.push(i); // 将当前柱子的索引入栈
}
return sum; // 返回总的接雨水量
}
};
算法的时间复杂度为O(n),空间复杂度为O(n)。
柱状图中最大的矩形
84. 柱状图中最大的矩形 - 力扣(LeetCode)
暴力解法
类似上题的想法,对每个列i找到左方第一个高度小于它的列left和右方第一个高度小于它的列right,面积为(right - left - 1) * heights[i]。同样,算法的时间复杂度为O(n^2),空间复杂度为O(1)。
class Solution {
public:
int largestRectangleArea(vector<int>& heights) {
int sum = 0; // sum 用于存储最大矩形面积
for (int i = 0; i < heights.size(); i++) { // 遍历数组中的每个元素
int left = i; // 初始化左边边界为当前柱子
int right = i; // 初始化右边边界为当前柱子
// 向左扫描,找到左边第一个高度小于当前柱子的位置
for (left = i; left >= 0; left--) {
if (heights[left] < heights[i]) break;
}
// 向右扫描,找到右边第一个高度小于当前柱子的位置
for (right = i; right < heights.size(); right++) {
if (heights[right] < heights[i]) break;
}
// 计算以当前柱子为高的矩形面积
int w = right - left - 1; // 矩形的宽度
int h = heights[i]; // 矩形的高,即当前柱子的高度
sum = max(sum, w * h); // 更新最大矩形面积
}
return sum; // 返回最大矩形面积
}
};
超时。
双指针法
有些难度,参考代码随想录代码随想录 (programmercarl.com)
class Solution {
public:
int largestRectangleArea(vector<int>& heights) {
vector<int> minLeftIndex(heights.size());
vector<int> minRightIndex(heights.size());
int size = heights.size();
// 记录每个柱子 左边第一个小于该柱子的下标
minLeftIndex[0] = -1; // 注意这里初始化,防止下面while死循环
for (int i = 1; i < size; i++) {
int t = i - 1;
// 这里不是用if,而是不断向左寻找的过程
while (t >= 0 && heights[t] >= heights[i]) t = minLeftIndex[t];
minLeftIndex[i] = t;
}
// 记录每个柱子 右边第一个小于该柱子的下标
minRightIndex[size - 1] = size; // 注意这里初始化,防止下面while死循环
for (int i = size - 2; i >= 0; i--) {
int t = i + 1;
// 这里不是用if,而是不断向右寻找的过程
while (t < size && heights[t] >= heights[i]) t = minRightIndex[t];
minRightIndex[i] = t;
}
// 求和
int result = 0;
for (int i = 0; i < size; i++) {
int sum = heights[i] * (minRightIndex[i] - minLeftIndex[i] - 1);
result = max(sum, result);
}
return result;
}
};算法的时间复杂度为O(n),空间复杂度也为O(n)。
单调栈法
代码随想录 (programmercarl.com)
明天补








![[SAP ABAP] 数据字典](https://img-blog.csdnimg.cn/direct/482fc68b72ae40b8ad511ed1d07fc264.png)