本文介绍使用Python工具seaborn详细实现分类关系图表，包含8类图141个代码模版。

分类关系图表用于展示数字变量和一个或多个分类变量之间的关系，可以进一步分为：箱形图（box plot）、增强箱形图（enhanced box plot）、小提琴图（violin plot）、抖动散点图（jitter plot）、蜂群图（beeswarm plot）、点图（point plot）、柱状图（bar plot）、分类柱状图（count plot ）。

所有模版👉：12.3万字+500多张图形+8000行代码......

---

 柱状图（bar plot）

柱状图（bar plot）表示了一个数值变量的聚合或统计估计（比如和，中值，均值，详细介绍见后章节9.3.2.6 柱状图-6类统计方式），每个矩形的高度表示该估计，同时使用误差条指示该估计的不确定性。

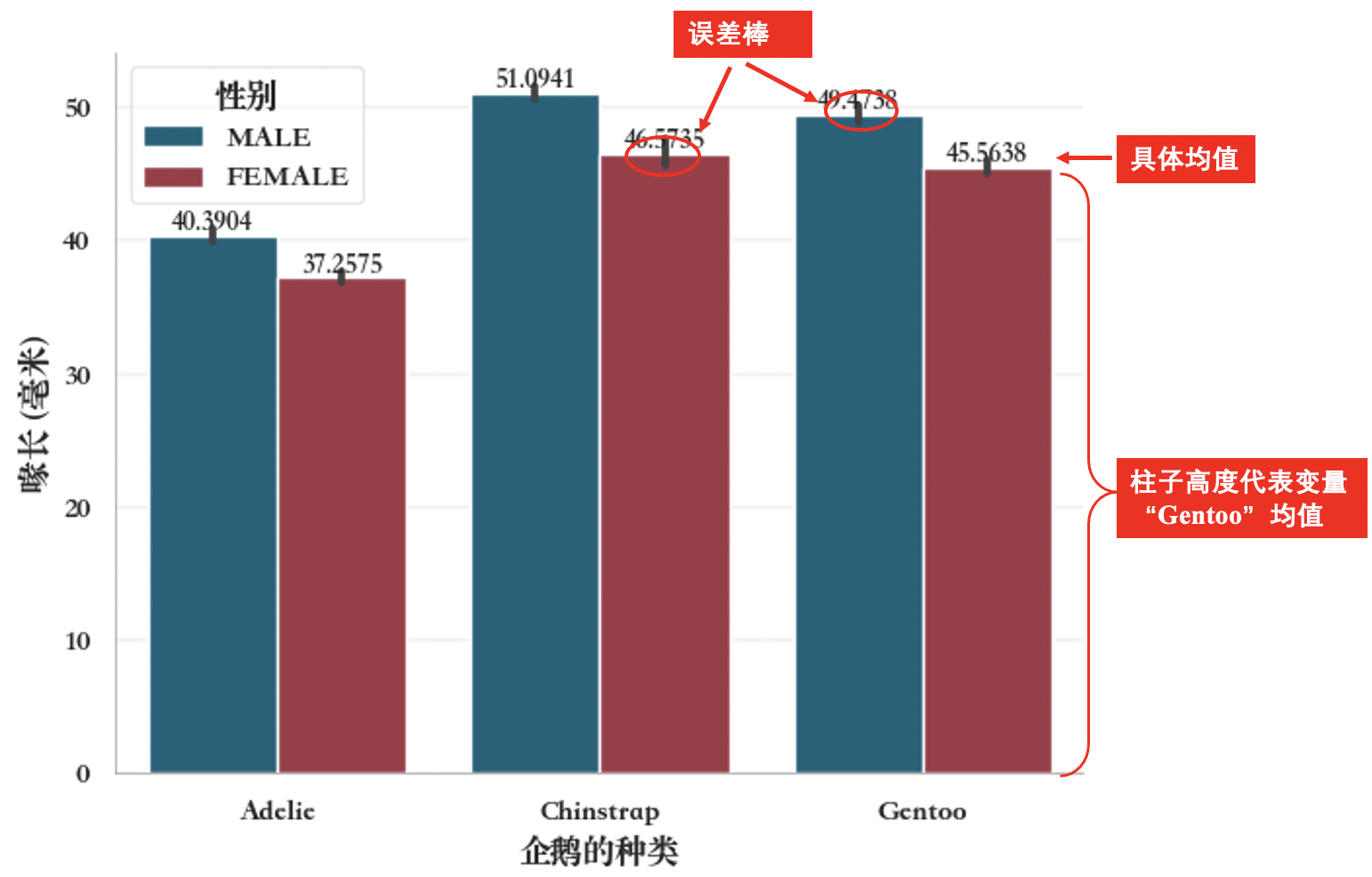
例如，柱状图-6类统计方式 ，

统计方式，即柱子高度代表变量的'mean'， 'median'，'sum'，'min'，'max'或者'std'之一，用图展示各中统计方式差异，

estimators = ['mean', 'median', 'sum', 'min', 'max', 'std']  #6种统计方式
fig, axs = plt.subplots(2, 3, figsize=(15, 10))
for i, estimator in enumerate(estimators):
    row = i // 3
    col = i % 3

    sns.barplot(
        x='企鹅的种类',
        y='喙长 (毫米)',
        data=penguins,
        estimator=estimator,  #设置不同的统计方式
        ax=axs[row, col],
        color="#a8a6a7")
    axs[row, col].set_title(f'统计方式: {estimator}')

plt.tight_layout()
plt.show()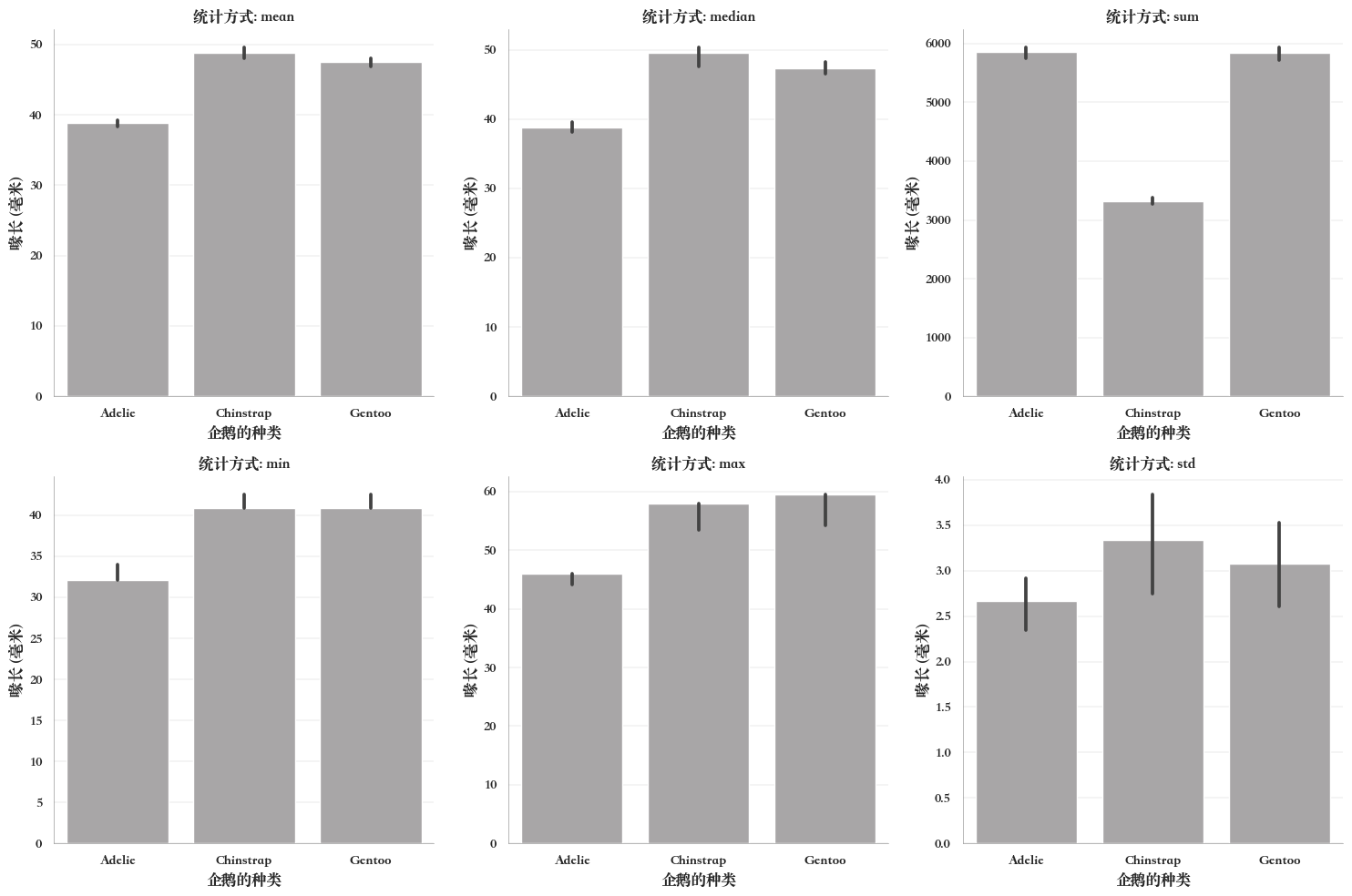

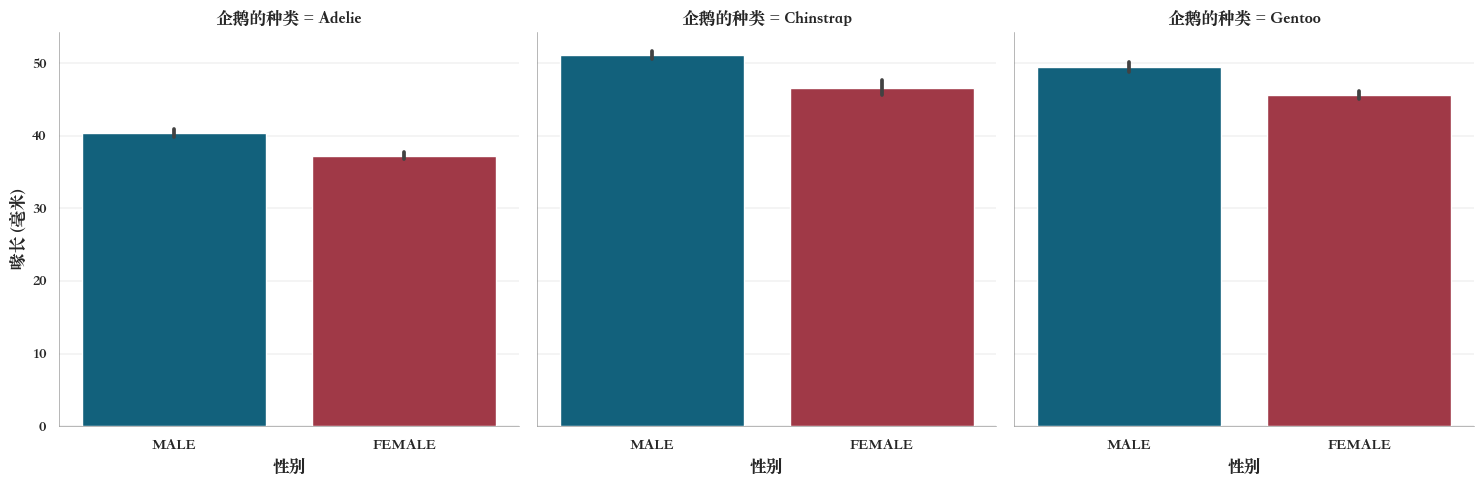
例如，柱状图-多子图，

sns.catplot(
    data=penguins,
    x="性别",
    y="喙长 (毫米)",
    col="企鹅的种类",  #列按照"岛屿"分面
    kind="bar",
    palette=["#006a8e", "#b1283a"],
)

---

分类柱状图（count plot ）

分类柱状图（count plot ）使用柱状图显示每个分类箱中的观测计数，这类图要区别于上文章节9.3.2 柱状图，用于直接显示每个类别中的观测数量，而不是间接统计计算一个新的统计量。

例如，分组分类柱状图，

g = sns.countplot(
    data=penguins,
    x="企鹅的种类",
    hue="性别",
    palette=["#006a8e", "#b1283a"],
)
#添加柱值文本标签
g.bar_label(g.containers[0], fontsize=10)
g.bar_label(g.containers[1], fontsize=10)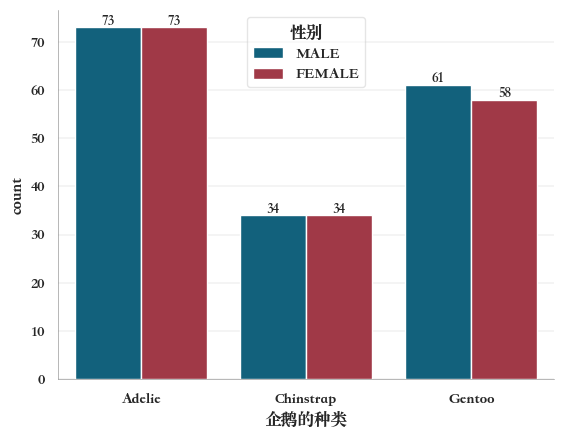

---

箱形图（box plot）

箱形图（box plot）直观地展示数据的关键指标（如下四分位数Q1、上四分位数Q3、中位数、平均值、异常值点），如下图，

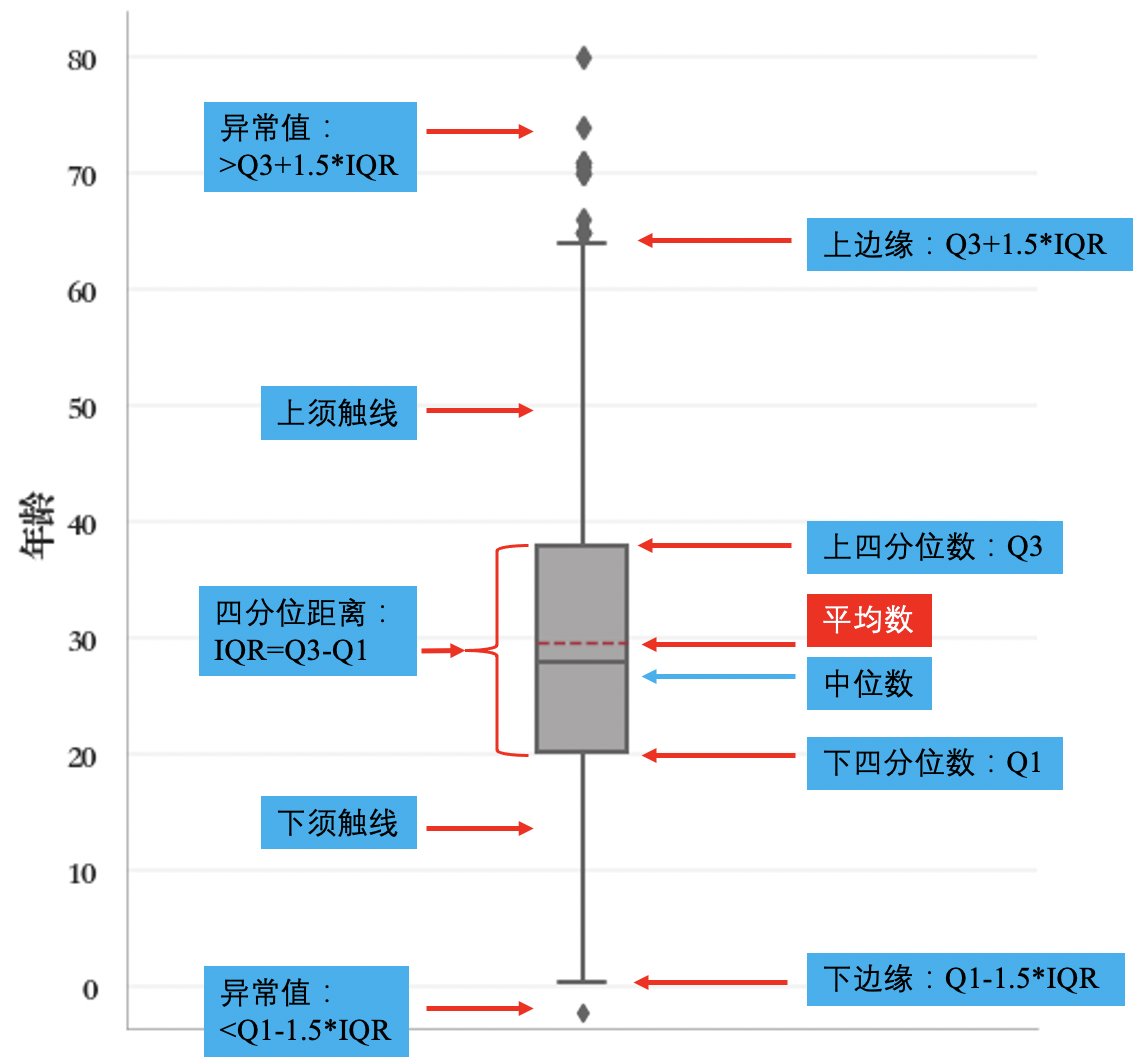
通过箱图可比较几组数据的分布情况，检查数据异常值，比较不同分布数据的偏态和尾重等。

例如，单组箱图，

sns.catplot(
    data=titanic,
    y="年龄",
    showmeans=True,  #显示平均数
    meanline=True, #显示平均数线
    meanprops={  #平均数线个性化
        'linestyle': '--', #线型
        'color': '#b1283a', #线颜色
        'linewidth': 1, #线宽
    },
    kind="box",
    width=0.1,
    color="#a8a6a7")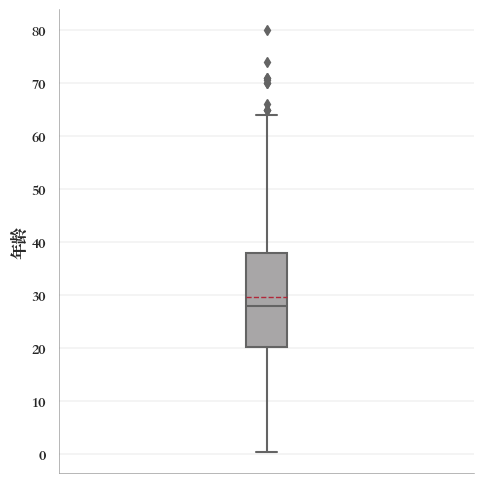

例如，多子图箱图，

sns.catplot(
    data=titanic,
    x="登船港口",
    y="年龄",
    hue="性别",
    col="船票等级",  #列按照"船票等级"分面
    row="获救情况",  #行按照"获救情况"分面
    width=0.7,
    linewidth=0.6,
    kind="box",
    palette=["#006a8e", "#b1283a"])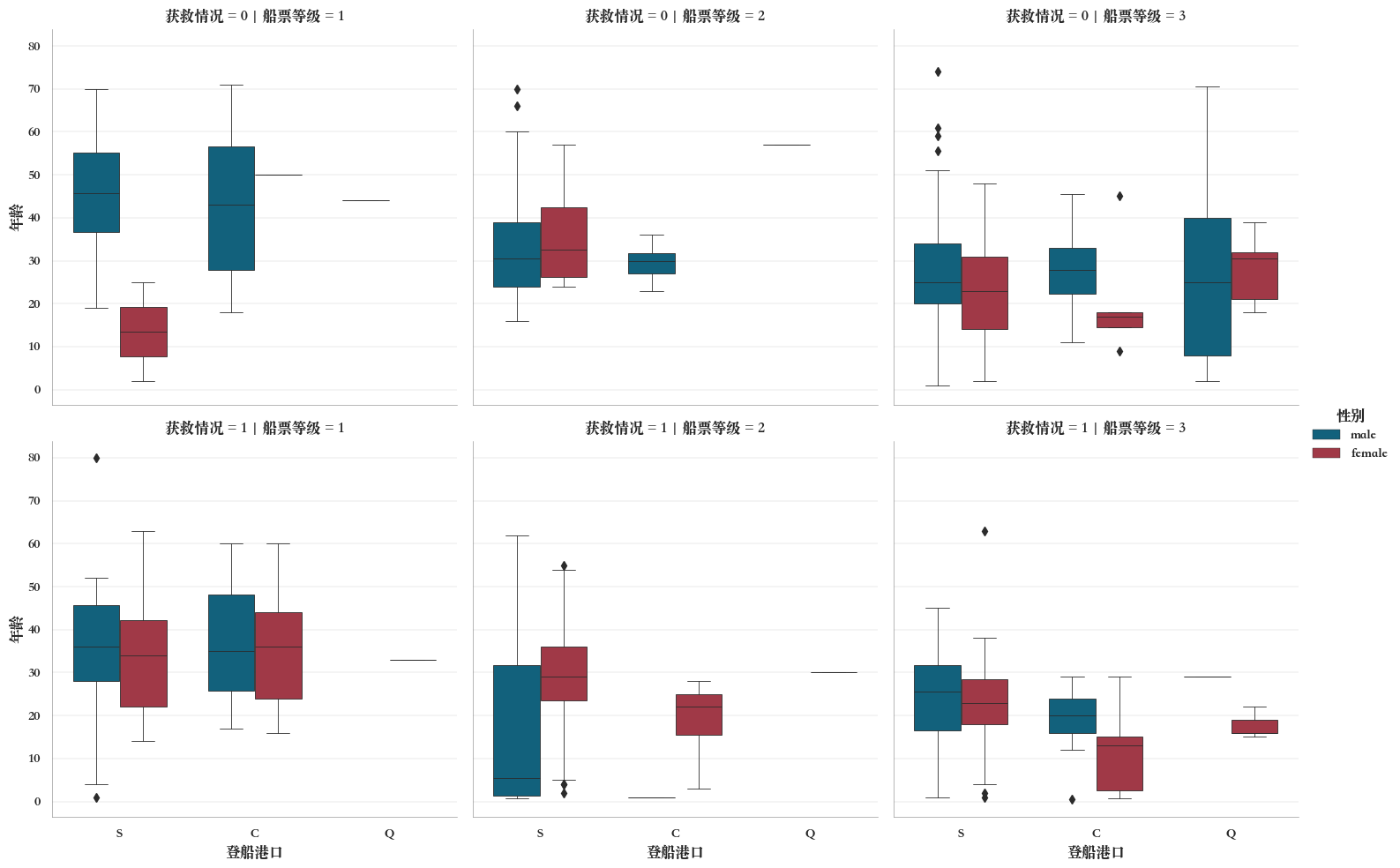

---

增强箱形图（enhanced box plot）

增强箱形图（enhanced box plot），又称作“Letter-value plots”，类似于箱形图，但是，能展示更多的分位数，提供更多关于数据分布形状的信息，特别是在尾部数据和异常值数据中，它更适用于较大的数据集（数据size：10,000-100,000），

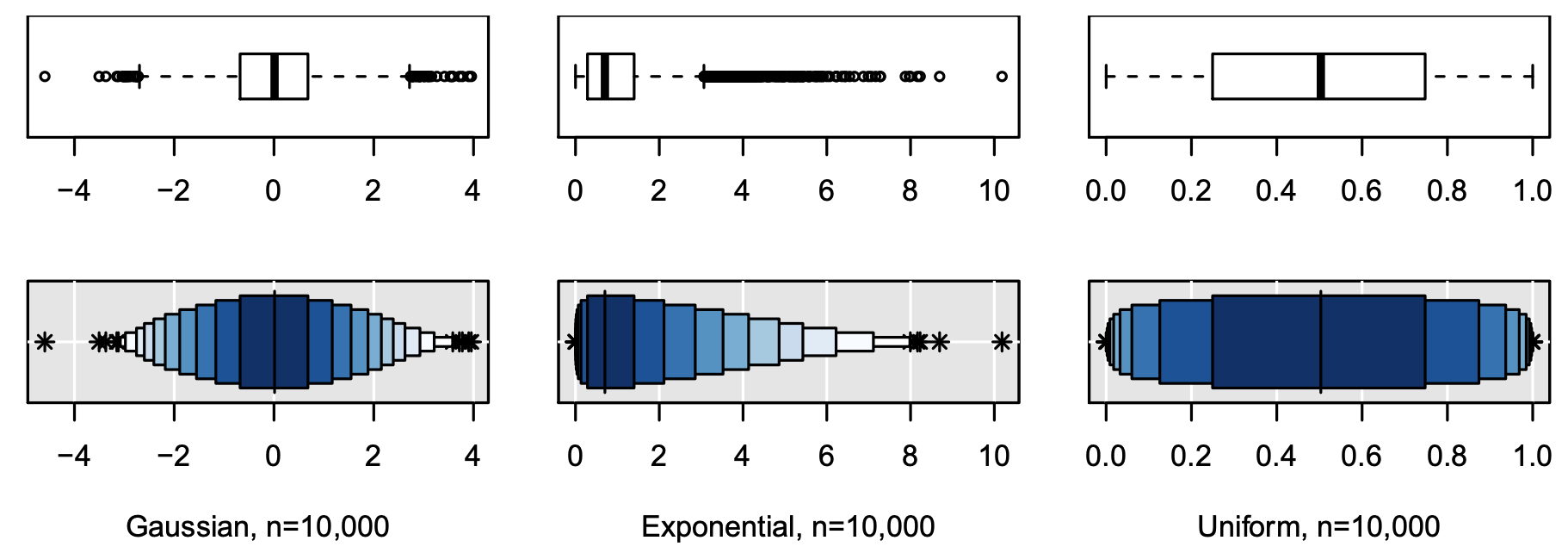
早期也是由Hadley Wickham等大佬提出，进一步学习：Letter-value plots: Boxplots for large data

例如，分组增强箱形图-垂直方向，

sns.catplot(
    data=diamonds,
    x="净度",  #垂直方向按照"净度"分组
    y="价格 ($)",
    width=0.5,
    kind="boxen",
    color="#a8a6a7")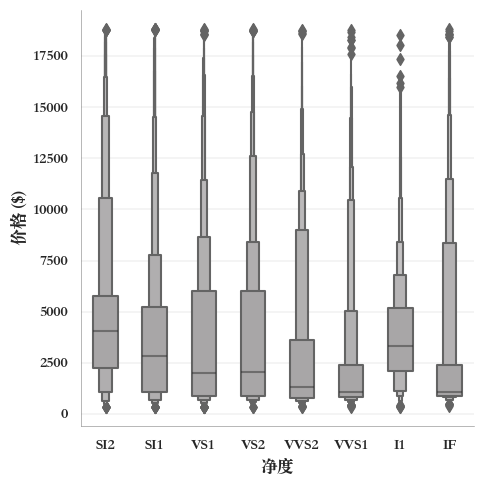

例如，分组增强箱形图-垂直方向，进一步分组，

sns.catplot(
    data=diamonds[diamonds['切工'].isin(['Fair', 'Very Good'])],
    x="净度",
    y="价格 ($)",
    hue="切工",
    width=0.8,
    kind="boxen",
    palette=["#006a8e", "#b1283a"],  #箱子颜色个性化设置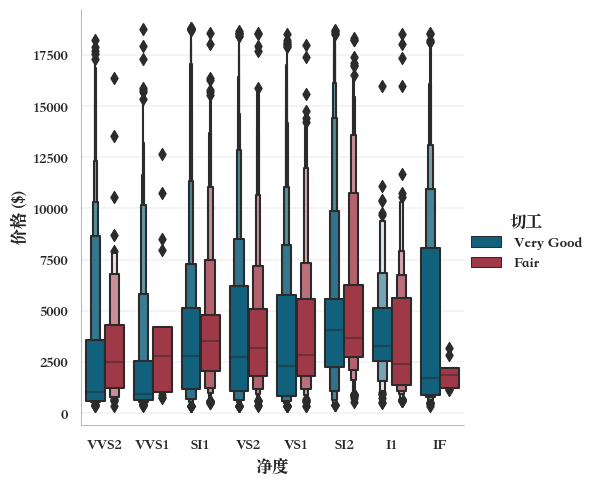

---

小提琴图（violin plot）

小提琴图（violin plot）本质上是由外部核密度图（上文章节“8.2 核密度图”）和内部箱形图（上文章节“9.1.1 箱形图”）两种基本图形结合而来的，核密度图展示数据概率密度（数据在某个值附近出现的频率，可展示数据在整个范围内的分布），箱形图展示数据分布状态（例如中位数，平均值，分位数，异常值等）！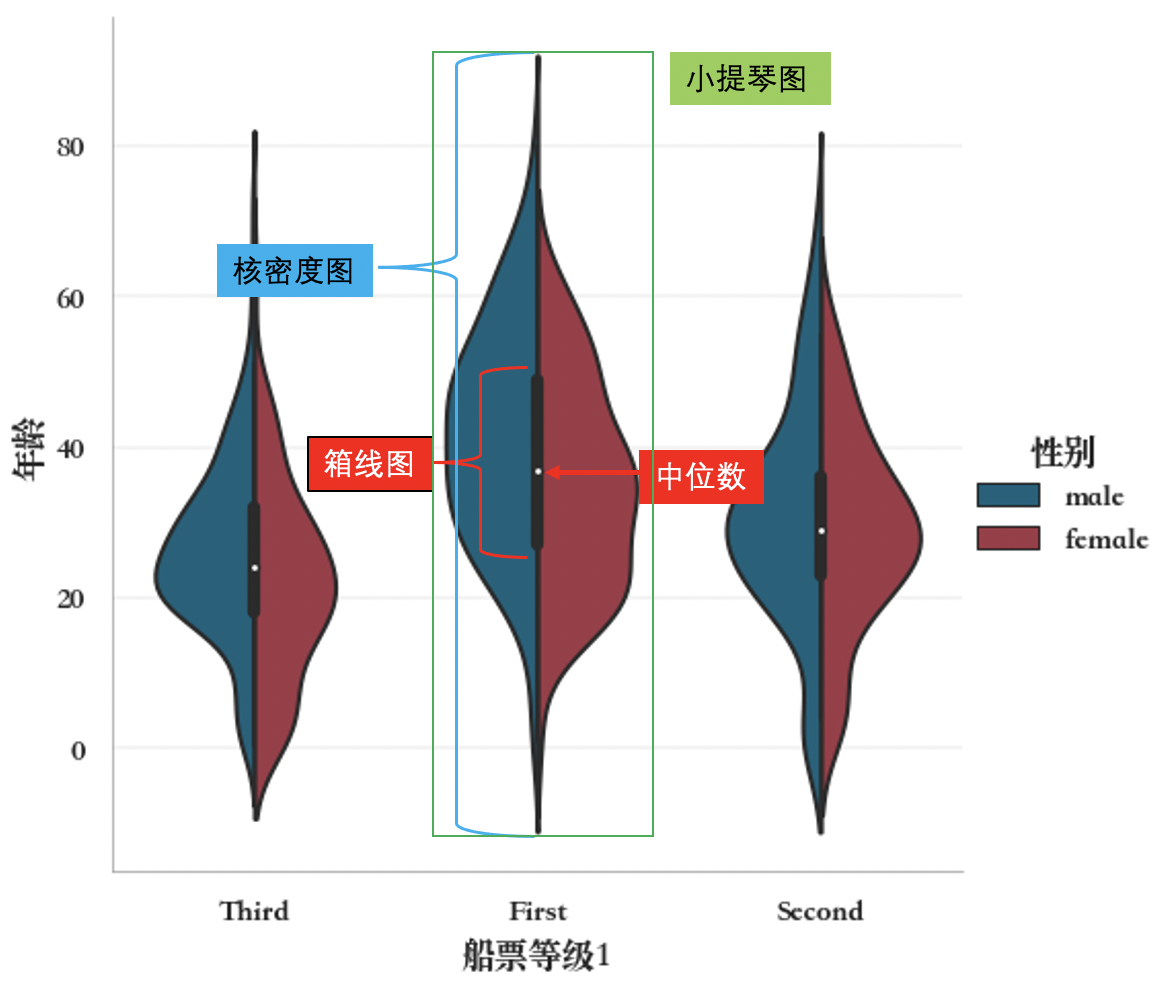

例如，分组小提琴图， 

sns.catplot(
    data=titanic,
    x="船票等级1",
    y="年龄",
    hue="性别",  #颜色随着"性别"变化
    width=0.7,
    kind="violin",
    color="#a8a6a7")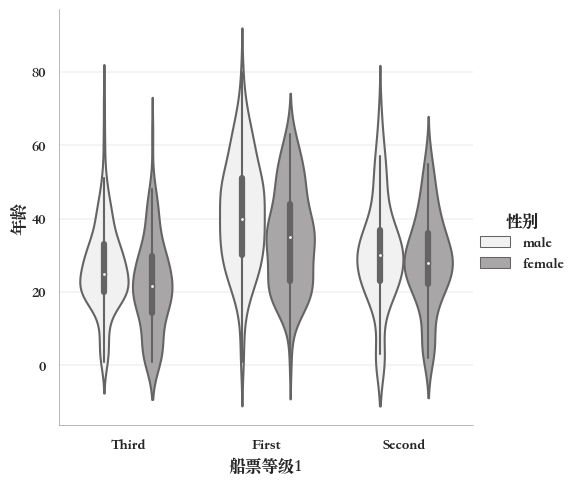

---

抖动散点图（jitter plot）

抖动散点图（jitter plot），是一类特殊的散点图，在一般散点图的基础上通过添加一些小幅度的随机抖动（jitter），调整分类轴上点的位置，在统计图表中，抖动可以使数据点在某个方向上稍微分散，以更清晰地展示分布。

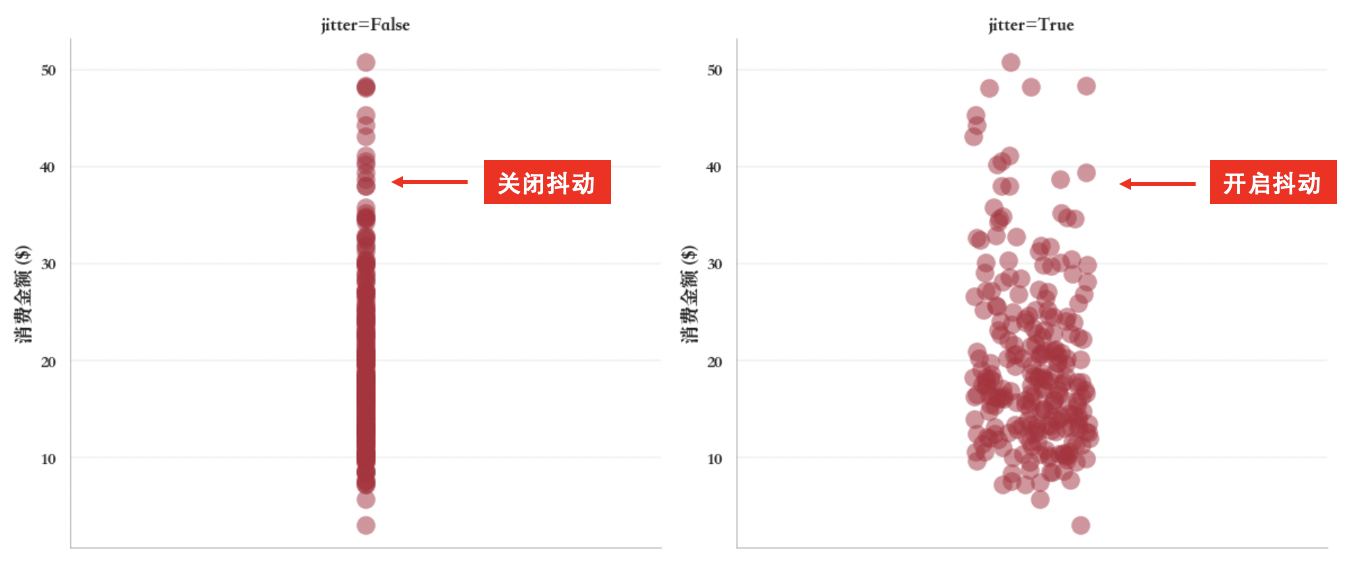
例如，分组抖动散点图，

sns.catplot(
    data=tips,
    y="消费金额 ($)",
    x="客人性别",
    hue="是否吸烟",
    dodge=True,  #和hue一起使用，对x指定的变量进一步分组
    size=12,
    alpha=0.5,
    kind="strip",
    palette=["#006a8e", "#b1283a"])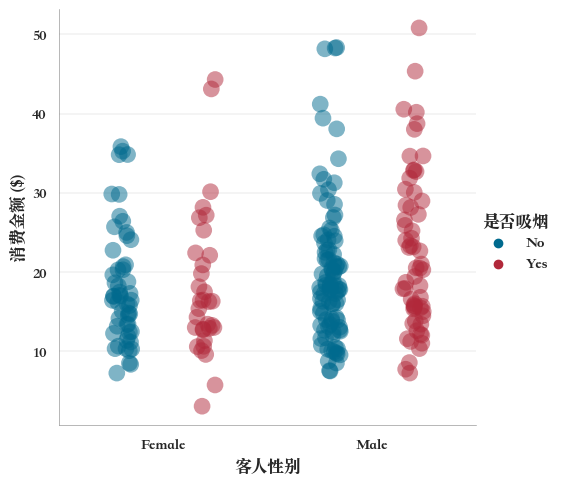

---

蜂群图（beeswarm plot）

蜂群图（beeswarm plot），似一群蜜蜂集聚在一起而得名，类似上文章节9.2.1抖动散点图，但是使用一种算法调整了点的位置（只沿着分类轴，注意区别于抖动散点图的随机抖动），以避免它们重叠。这样可以更好地展示数值的分布，但是对于大量的观测值来说不适用。

例如，分组蜂群图，

sns.catplot(
    data=tips,
    y="消费金额 ($)",
    x="客人性别",
    hue="是否吸烟",
    dodge=True,  #和hue一起使用，对x指定的变量进一步分组
    size=6,
    kind="swarm",
    palette=["#006a8e", "#b1283a"])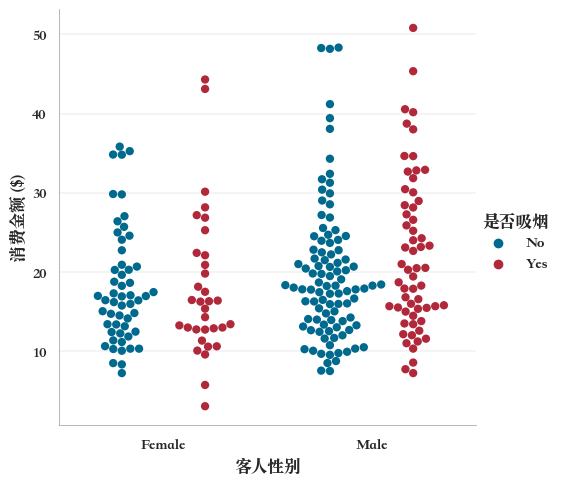

---

点图（point plot）

点图（point plot）通过点的位置表示数值变量的中心趋势估计，并使用误差条（error bar）来显示估计值的不确定性范围，可以集中地比较一个或多个分类变量的不同水平。

例如，点图-4类误差棒方案 ，

errorbars = ['ci', 'pi', 'se', 'sd']  #4类误差棒方案
fig, axs = plt.subplots(2, 2, figsize=(12, 10))

for i, errorbar in enumerate(errorbars):
    row = i // 2
    col = i % 2

    sns.pointplot(
        x='企鹅的种类',
        y='喙长 (毫米)',
        data=penguins,
        errorbar=errorbar,  #设置误差棒方案
        ax=axs[row, col],
        color="#a8a6a7")
    axs[row, col].set_title(f'误差棒方案: {errorbar}')
plt.tight_layout()
plt.show()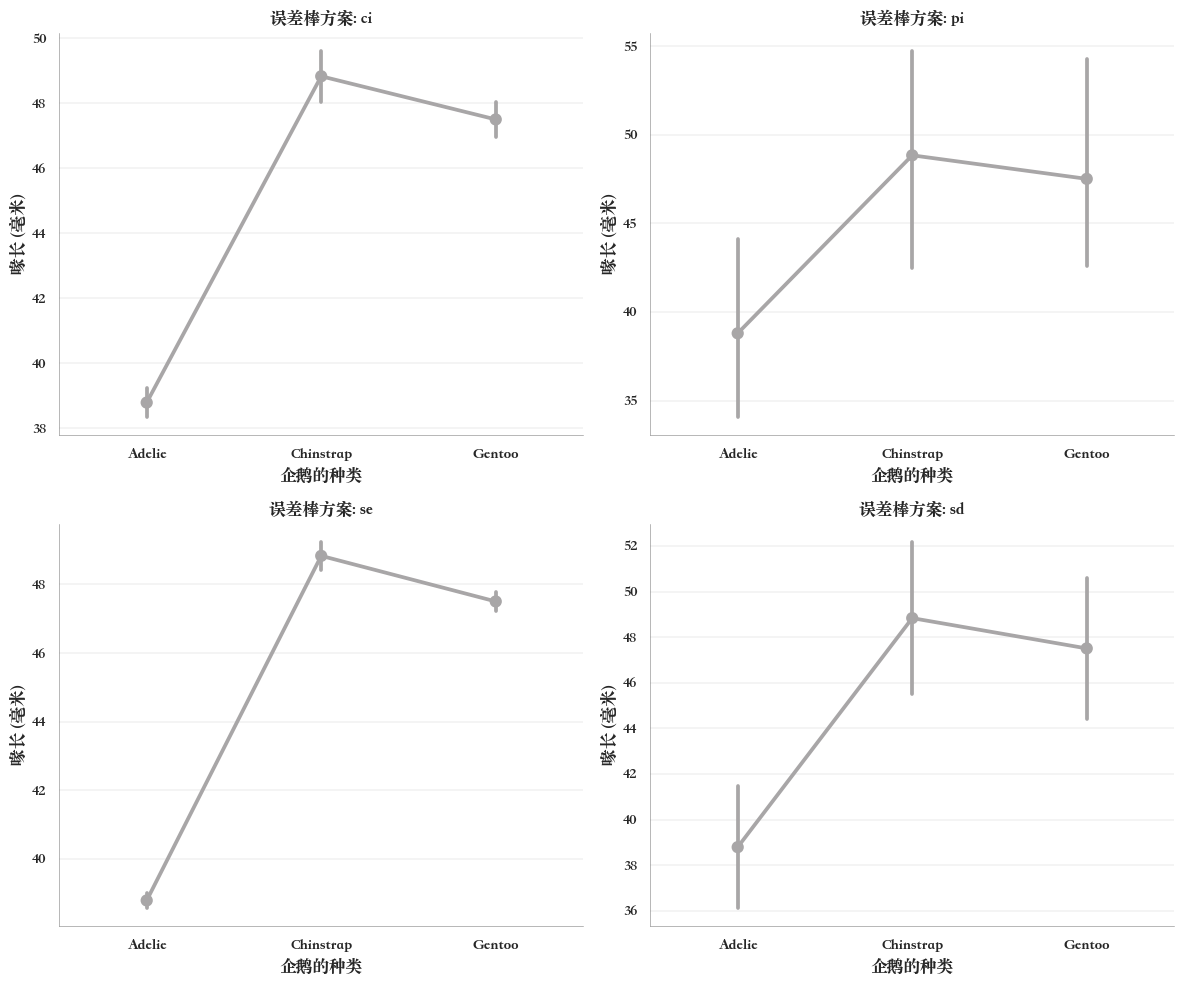

---

以上只展示部分模版，更多模版，

👉：12.3万字+500多张图形+8000行代码......