https://arxiv.org/abs/2108.01073

摘要

引导图像合成技术使普通用户能够以最小的努力创建和编辑逼真的图像。关键挑战在于平衡对用户输入（例如，手绘的彩色笔画）的忠实度和合成图像的真实感。现有的基于GAN的方法试图通过使用条件GAN或GAN反演来实现这种平衡，这些方法具有挑战性，通常需要为每个应用单独提供额外的训练数据或损失函数。为了解决这些问题，我们引入了一种基于扩散模型生成先验的新图像合成和编辑方法，即随机微分编辑（SDEdit），该方法通过迭代去噪和随机微分方程（SDE）生成逼真的图像。给定用户引导的输入图像（如操控RGB像素），SDEdit首先向输入图像添加噪声，然后通过SDE先验逐步去噪以增加其真实感。SDEdit不需要特定任务的训练或反演，并且可以自然地实现真实感和忠实度之间的平衡。根据一项人类感知研究，在多项任务（包括基于笔画的图像合成和编辑以及图像合成）中，SDEdit在真实感上优于最先进的基于GAN的方法，最高达到98.09%，在总体满意度得分上最高达到91.72%。

引言

现代生成模型可以从随机噪声中创建逼真的图像（Karras et al., 2019；Song et al., 2021），成为视觉内容创作的重要工具。特别感兴趣的是引导图像合成和编辑，用户指定一般的引导（如粗略的彩色笔画），生成模型学习填充细节（见图1）。引导图像合成有两个自然的需求：生成的图像应显得逼真，并且忠实于用户引导的输入，从而使有无艺术专长的人都能从不同细节层次创建逼真的图像。

现有方法通常通过两种途径实现这种平衡。第一类方法利用条件GAN（Isola et al., 2017；Zhu et al., 2017），直接从原始图像到编辑图像进行映射。不幸的是，对于每个新的编辑任务，这些方法需要数据收集和模型再训练，既昂贵又耗时。第二类方法利用GAN反演（Zhu et al., 2016；Brock et al., 2017；Abdal et al., 2019；Gu et al., 2020；Wu et al., 2021；Abdal et al., 2020），使用预训练的GAN将输入图像反演为潜在表示，随后修改以生成编辑后的图像。该过程涉及为不同图像编辑任务手动设计损失函数和优化过程。此外，有时可能无法找到忠实代表输入的潜在代码（Bau et al., 2019b）。

为了在避免上述挑战的同时平衡真实感和忠实度，我们引入了SDEdit，一种利用生成随机微分方程（SDEs；Song et al., 2021）的引导图像合成和编辑框架。类似于紧密相关的扩散模型（Sohl-Dickstein et al., 2015；Ho et al., 2020），基于SDE的生成模型通过迭代去噪将初始高斯噪声向量平滑地转换为逼真的图像样本，其无条件图像合成性能可与或优于GANs（Dhariwal & Nichol, 2021）。SDEdit的关键直觉是“劫持”基于SDE的生成模型的生成过程，如图2所示。给定用户引导输入的图像（如笔画绘画或带笔画编辑的图像），我们可以添加适量噪声以平滑不良的伪影和失真（例如，笔画像素处的不自然细节），同时保留输入用户引导的整体结构。然后我们使用这个噪声输入初始化SDE，并逐步去除噪声以获得既真实又忠实于用户引导输入的去噪结果（见图2）。

与条件GAN不同，SDEdit不需要为每个新任务收集训练图像或用户注释；与GAN反演不同，SDEdit不需要设计额外的训练或任务特定损失函数。SDEdit只使用一个在未标记数据上训练的单一预训练SDE生成模型：给定操控RGB像素形式的用户引导，SDEdit向引导添加高斯噪声，然后运行逆向SDE以合成图像。SDEdit自然地找到了真实感和忠实度之间的平衡：当我们添加更多高斯噪声并运行SDE更长时间时，生成的图像更真实但忠实度较低。我们可以利用这一观察找到真实感和忠实度之间的适当平衡。

我们在三个应用中展示了SDEdit：基于笔画的图像合成、基于笔画的图像编辑和图像合成。我们展示了SDEdit可以从不同忠实度水平的引导中生成真实且忠实的图像。在基于笔画的图像合成实验中，根据人类判断，SDEdit在真实感评分上优于最先进的基于GAN的方法，最高达到98.09%，在总体满意度评分（衡量真实感和忠实度）上最高达到91.72%。在图像合成实验中，SDEdit在忠实度评分上表现更好，在用户研究中总体满意度评分上优于基线方法，最高达到83.73%。我们的代码和模型将在发布时提供。

背景：使用随机微分方程（SDEs）进行图像合成

随机微分方程（SDEs）通过在动力学中引入随机噪声来推广常微分方程（ODEs）。SDE的解是一个随时间变化的随机变量（即随机过程），我们将其表示为$x(t)\in {\mathbb{R}}^d$，其中$t\in [0,1]$表示时间。在图像合成中（Song et al., 2021），我们假设$x(0)\sim p_0=p_{data}$表示数据分布中的一个样本，并且前向SDE通过高斯扩散生成$t\in (0,1]$的$x(t)$。给定$x(0)$，$x(t)$分布为高斯分布：

$$x(t)=\alpha (t)x(0)+\sigma (t)z,z\sim \mathcal{N}(0,I),$$

其中，$z$是均值为0、协方差为单位矩阵I的高斯噪声，$\alpha (t)$和$\sigma (t)$是时间$t$的函数。

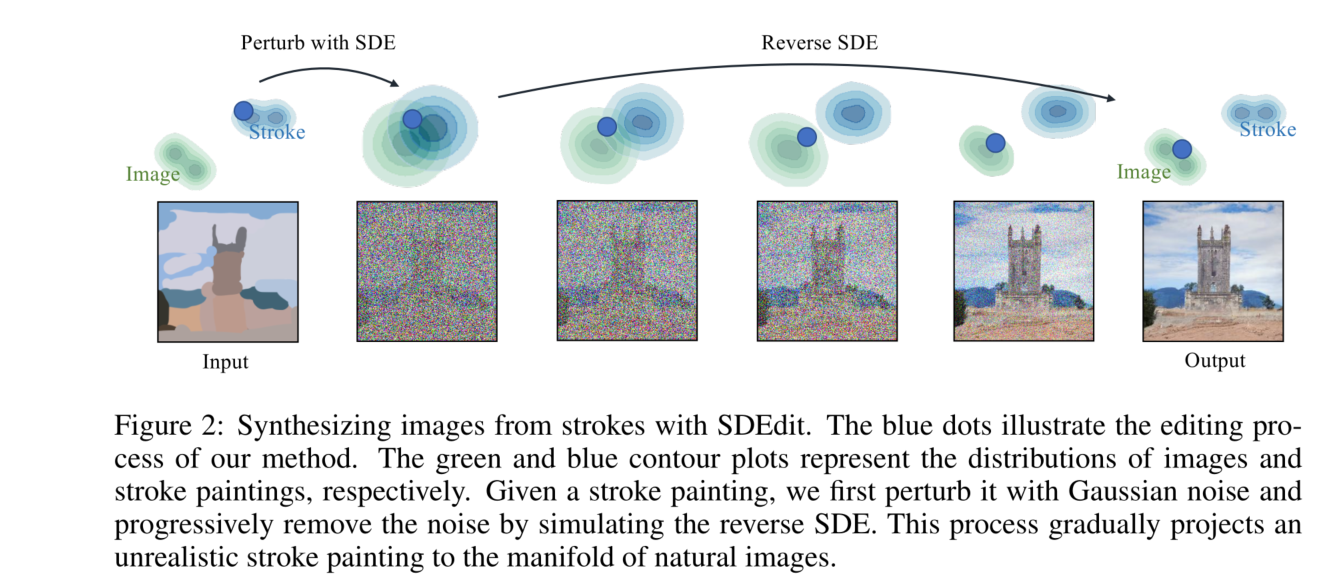
图2：使用SDEdit从笔画合成图像。蓝点表示我们方法的编辑过程。绿色和蓝色的等高线图分别代表图像和笔画绘画的分布。给定一个笔画绘画，我们首先用高斯噪声对其进行扰动，然后通过模拟逆向SDE逐步去除噪声。这个过程逐渐将不真实的笔画绘画投影到自然图像的流形上。

其中，$\sigma (t):[0,1]\to [0,\infty )$ 是描述噪声 $z$ 大小的标量函数，$\alpha (t):[0,1]\to [0,1]$ 是表示数据 $x(0)$ 大小的标量函数。$x(t)$ 的概率密度函数表示为 $p_t$。

通常考虑两种类型的SDE：方差爆发SDE（VE-SDE）在所有时间$t$上都有 $\alpha (t)=1$，且 $\sigma (1)$ 为一个较大的常数，因此 $p_1$ 接近于 $N(0,{\sigma }^2(1)I)$；而方差保持SDE（VP-SDE）满足 ${\alpha }^2(t)+{\sigma }^2(t)=1$，且随着$t$趋向1，$\alpha (t)\to 0$，因此 $p_1$ 等于 $N(0,I)$。无论是VE-SDE还是VP-SDE，都在时间从0到1的过程中将数据分布转换为随机高斯噪声。为了简便起见，本文其余部分将基于VE-SDE讨论细节，并在附录C中讨论VP-SDE的过程。尽管它们的形式略有不同，并且在不同图像域中的表现也有所不同，但它们具有相同的数学直觉。

使用VE-SDE进行图像合成

在这些定义下，我们可以将图像合成问题表述为从噪声观测$x(t)$中逐渐去除噪声以恢复$x(0)$。这可以通过逆向SDE来实现，该SDE从$t=1$到$t=0$进行，基于对噪声扰动得分函数${\nabla }_x\log p_t(x)$的了解。例如，VE-SDE的采样过程由以下（逆向）SDE定义：

$$dx(t)=\left(-\frac{d[{\sigma }^2(t)]}{dt}{\nabla }_x\log p_t(x)\right)dt+\sqrt{\frac{d[{\sigma }^2(t)]}{dt}}d\bar{w},$$

其中 $\bar{w}$ 是时间从$t=1$到$t=0$逆向流动的维纳过程。如果我们设初始条件$x(1)\sim p_1=N(0,{\sigma }^2(1)I)$，则$x(0)$的解将分布为$p_{data}$。实际上，可以通过去噪得分匹配（Vincent, 2011）学习噪声扰动得分函数。记学习到的得分模型为$s_{\theta }(x(t),t)$，时间$t$的学习目标为：

$$L_t={\mathbb{E}}_{x(0)\sim p_{data},z\sim \mathcal{N}(0,I)}\left[{\Vert {\sigma }_t{s}_{\theta }(x(t),t)-z\Vert }_2^2\right],$$

其中 $p_{data}$ 是数据分布，$x(t)$ 的定义如公式1。总体训练目标是各个时间$t$学习目标$L_t$的加权和，Ho et al. (2020) 和 Song et al. (2020; 2021) 讨论了各种加权方法。

通过参数化得分模型$s_{\theta }(x(t),t)$ 来逼近 ${\nabla }_x\log p_t(x)$，可以使用Euler-Maruyama方法近似SDE的解；从时间 $(t+\Delta t)$ 到 $t$ 的更新规则为：

$$x(t)=x(t+\Delta t)+({\sigma }^2(t)-{\sigma }^2(t+\Delta t))s_{\theta }(x(t),t)+\sqrt{{\sigma }^2(t)-{\sigma }^2(t+\Delta t)}z,$$

其中 $z\sim \mathcal{N}(0,I)$。我们可以选择从1到0的特定时间间隔离散化，初始化 $x(0)\sim N(0,{\sigma }^2(1)I)$ 并通过公式4迭代生成图像$x(0)$。

引导图像合成与编辑方法SDEdit

在本节中，我们介绍SDEdit，并描述如何通过预训练于未标记图像上的SDE模型进行引导图像合成和编辑。

设置

用户提供一个完整分辨率的图像$x^{(g)}$，以操控RGB像素的形式，这被称为“引导”。引导可能包含不同层次的细节：高层次引导仅包含粗略的彩色笔画，中层次引导在真实图像上包含彩色笔画，低层次引导在目标图像上包含图像补丁。我们在图1中展示了这些引导，普通用户可以轻松提供这些引导。我们的目标是生成满足以下两个需求的完整分辨率图像：

• 真实感：图像应显得逼真（例如，通过人类或神经网络评估）。
• 忠实度：图像应与引导$x^{(g)}$相似（例如，通过$L_2$距离衡量）。

需要注意的是，真实感和忠实度并不是正相关的，因为可以有不忠实的真实图像（例如，随机的真实图像）和不真实的忠实图像（例如，引导本身）。与常规逆问题不同，我们不假设关于测量函数（即，从真实图像到用户创建的RGB像素引导的映射）的知识，因此基于得分模型解决逆问题的技术（Dhariwal & Nichol, 2021；Kawar et al., 2021）和需要配对数据集的方法（Isola et al., 2017；Zhu et al., 2017）在此不适用。

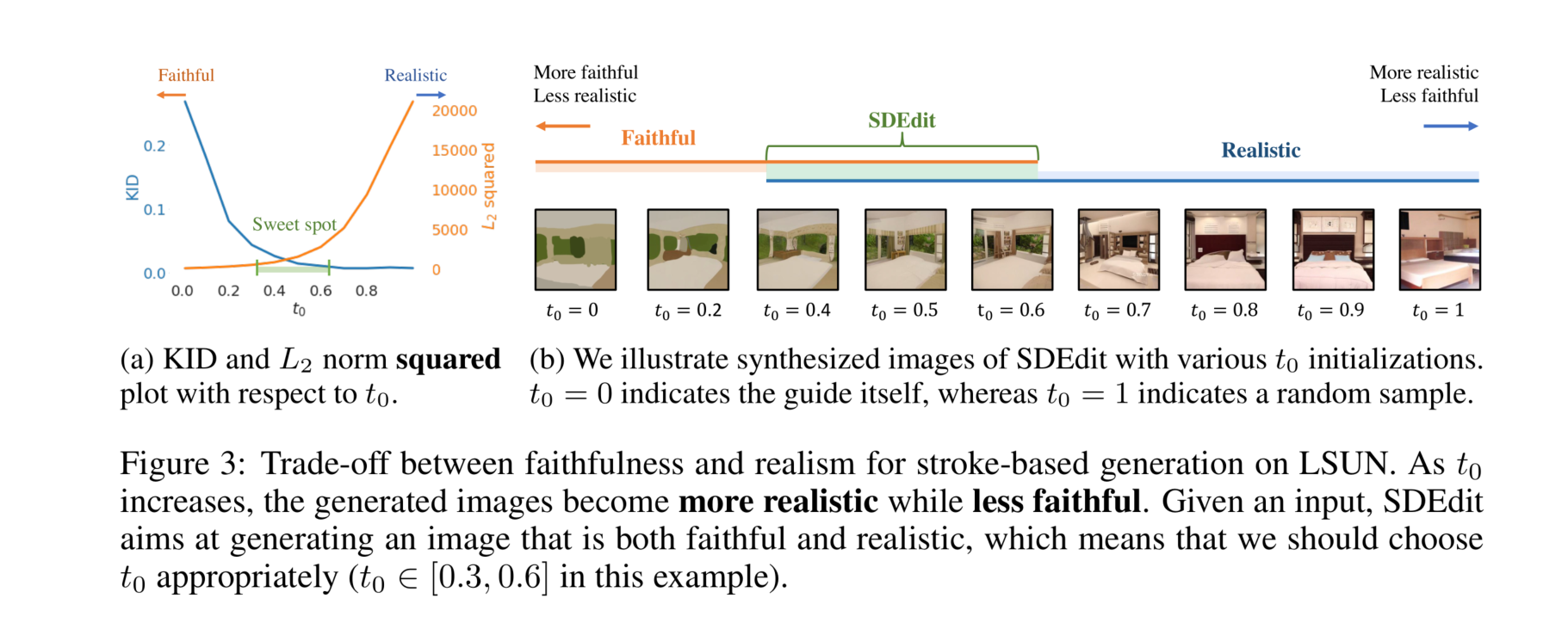
图3：在LSUN数据集上基于笔画生成的忠实度和真实感之间的权衡。随着$t_0$的增加，生成的图像变得更加真实但忠实度较低。给定一个输入，SDEdit的目标是生成既忠实又真实的图像，这意味着我们应适当地选择$t_0$（在本例中，$t_0\in [0.3,0.6]$）。

过程

我们的方法SDEdit利用了逆向SDE不仅可以从$t_0=1$解算，还可以从任意中间时间$t_0\in (0,1)$解算这一事实——这是以前基于SDE的生成模型没有研究过的途径。我们需要找到适当的初始化，从我们的引导中可以解算出逆向SDE，以获得理想的、真实的和忠实的图像。对于任何给定的引导$x^{(g)}$，我们将SDEdit过程定义如下：

1. 采样$x^{(g)}(t_0)\sim N(x^{(g)};{\sigma }^2(t_0)I)$，然后通过迭代公式4生成$x(0)$。

我们用SDEdit($x^{(g)};t_0,\theta$)表示上述过程。实际上，SDEdit选择一个特定的时间$t_0$，向引导$x^{(g)}$添加标准差为${\sigma }^2(t_0)$的高斯噪声，然后在$t=0$时解算相应的逆向SDE以生成合成的$x(0)$。

除了SDE解算器的离散化步骤外，SDEdit的关键超参数是$t_0$，即我们在逆向SDE中开始图像合成过程的时间。在下面，我们描述了一个真实感-忠实度权衡，允许我们选择合理的$t_0$值。

真实感-忠实度权衡

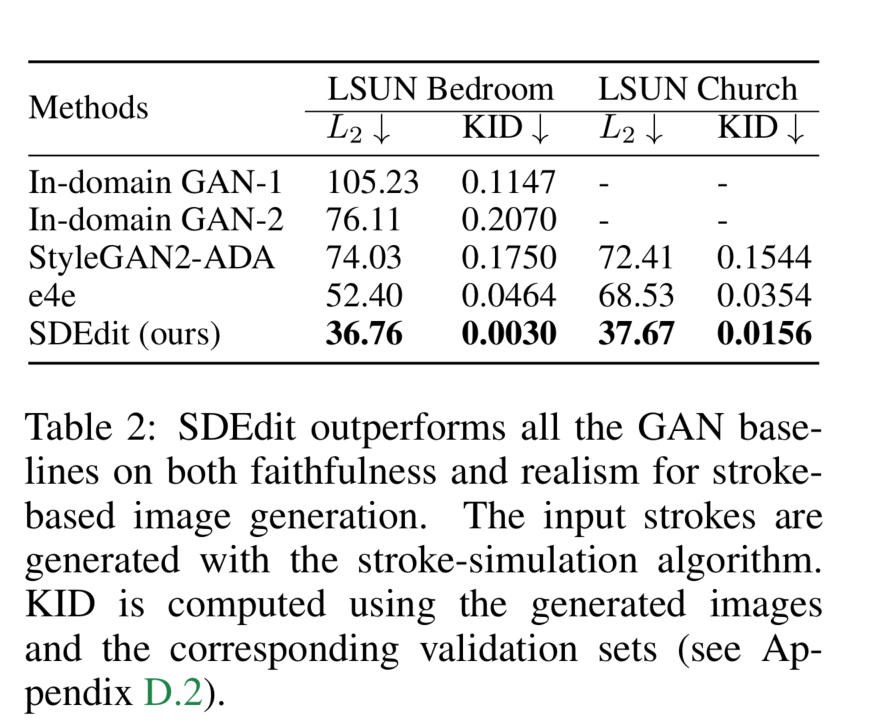
我们注意到，对于训练得当的SDE模型，选择不同的$t_0$值时存在真实感-忠实度权衡。为说明这一点，我们专注于LSUN数据集，并使用高层次笔画绘画作为引导进行基于笔画的图像生成。实验细节见附录D.2。我们考虑了同一输入下$t_0\in [0,1]$的不同选择。为了量化真实感，我们采用了用于比较图像分布的神经方法，如核插入评分（KID；Bińkowski et al., 2018）。如果合成图像与真实图像之间的KID较低，则合成图像是真实的。对于忠实度，我们测量合成图像与引导$x^{(g)}$之间的$L_2$距离。从图3中，我们观察到随着$t_0$增加，真实感增加但忠实度下降。

真实感-忠实度权衡可以从另一个角度解释。如果引导远离任何真实图像，那么为了生成真实的图像，我们必须容忍至少一定程度的偏离引导（不忠实），这一点在以下命题中有所说明。

命题1 假设$||s_{\theta }(x,t)|{|}_2^2\le C$对于所有$x\in X$和$t\in [0,1]$成立。那么，对于所有$\delta \in (0,1)$，以至少$(1-\delta )$的概率有：

$$||x^{(g)}-\text{SDEdit}(x^{(g)};t_0,\theta )|{|}_2^2\le {\sigma }^2(t_0)(C{\sigma }^2(t_0)+d+2\sqrt{-d\cdot \log \delta }-2\log \delta )$$

其中$d$是$x^{(g)}$的维度。我们在附录A中提供了证明。从高层次上讲，引导与合成图像的差异可以分解为得分的输出和随机高斯噪声；随着$t_0$增加，二者都会增加，因此差异变大。上述命题表明，要使图像以高概率逼真，$t_0$必须足够大。反之，如果$t_0$过大，则对引导的忠实度恶化，SDEdit将生成随机的真实图像（极端情况下为无条件图像合成）。

$t_0$的选择

我们注意到，引导的质量可能会影响合成图像的整体质量。对于合理的引导，我们发现$t_0\in [0.3,0.6]$效果较好。然而，如果引导是一幅只有白色像素的图像，那么即使是模型分布中最接近的“真实”样本也可能相当远，我们必须选择较大的$t_0$以牺牲忠实度来换取更好的真实感。在交互设置中（用户绘制基于草图的引导），我们可以初始化$t_0\in [0.3,0.6]$，用SDEdit合成一个候选样本，然后询问用户样本是否应该更忠实或更真实；根据响应，我们可以通过二分搜索获得合理的$t_0$。在大规模非交互设置中（我们获得一组已生成的引导），我们可以在随机选择的图像上进行类似的二分搜索以获得$t_0$，然后在同一任务中的所有引导上固定$t_0$。尽管不同的引导可能有不同的最佳$t_0$，但我们经验观察到共享的$t_0$对同一任务中的所有合理引导效果良好。

详细算法及扩展

我们在算法1中展示了VE-SDE的一般算法。由于篇幅限制，我们在附录C中描述了VP-SDE的详细算法。实质上，该算法是用于求解SDEdit($x^{(g)};t_0,\theta$)的Euler-Maruyama方法。对于希望保留合成图像某些部分与引导相同的情况，我们还可以引入一个额外的通道，以屏蔽不希望编辑的图像部分。这是对主文中提到的SDEdit过程的轻微修改，我们在附录C.2中讨论了详细内容。

图4：在基于笔画生成（LSUN卧室）中，SDEdit生成的图像比最先进的基于GAN的模型更真实且更忠实。前两行的引导是由人类创建的，后两行的引导是由算法模拟的。

相关工作

条件GANs

条件GANs用于图像编辑（Isola et al., 2017；Zhu et al., 2017；Jo & Park, 2019；Liu et al., 2021）通过用户输入直接生成图像，并在各种任务中展示了成功，包括图像合成和编辑（Portenier et al., 2018；Chen & Koltun, 2017；Dekel et al., 2018；Wang et al., 2018；Park et al., 2019；Zhu et al., 2020b；Jo & Park, 2019；Liu et al., 2021）、图像修复（Pathak et al., 2016；Iizuka et al., 2017；Yang et al., 2017；Liu et al., 2018）、照片着色（Zhang et al., 2016；Larsson et al., 2016；Zhang et al., 2017；He et al., 2018）、语义图像纹理和几何合成（Zhou et al., 2018；Guérin et al., 2017；Xian et al., 2018）。这些方法在使用用户草图或颜色进行图像编辑时也表现出色（Jo & Park, 2019；Liu et al., 2021；Sangkloy et al., 2017）。然而，条件模型必须在原始图像和编辑图像上进行训练，因此需要为新编辑任务收集数据和重新训练模型。因此，将这些方法应用于即时图像操作仍然具有挑战性，因为每个新应用都需要训练一个新模型。与条件GANs不同，SDEdit仅需要在原始图像上进行训练。因此，它可以在测试时直接应用于各种编辑任务，如图1所示。

GANs反演与编辑

另一种主流的图像编辑方法是GAN反演（Zhu et al., 2016；Brock et al., 2017），首先将输入投影到无条件GAN的潜在空间，然后从修改后的潜在代码合成新图像。在这方面提出了几种方法，包括为每个图像微调网络权重（Bau et al., 2019a；Pan et al., 2020；Roich et al., 2021），选择更好或多层次的投影和编辑（Abdal et al., 2019；2020；Gu et al., 2020；Wu et al., 2021），设计更好的编码器（Richardson et al., 2021；Tov et al., 2021），建模图像损坏和转换（Anirudh et al., 2020；Huh et al., 2020），以及发现有意义的潜在方向（Shen et al., 2020；Goetschalckx et al., 2019；Jahanian et al., 2020；Härkönen et al., 2020）。然而，这些方法需要为不同任务定义不同的损失函数，并且需要进行GAN反演，这对于各种数据集来说可能效率低下且不准确（Huh et al., 2020；Karras et al., 2020b；Bau et al., 2019b；Xu et al., 2021）。

其他生成模型

最近在训练非归一化概率模型方面取得了进展，如基于得分的生成模型（Song & Ermon, 2019；2020；Song et al., 2021；Ho et al., 2020；Song et al., 2020；Jolicoeur-Martineau et al., 2021）和能量基模型（Ackley et al., 1985；Gao et al., 2017；Du & Mordatch, 2019；Xie et al., 2018；2016；Song & Kingma, 2021），其图像样本质量与GANs相当。然而，以前大多数此方向的工作集中在无条件图像生成和密度估计，最先进的图像编辑和合成技术仍然以GANs为主。在这项工作中，我们专注于最近出现的基于随机微分方程（SDE）的生成建模，并研究其在可控图像编辑和合成任务中的应用。一项并行工作（Choi et al., 2021）使用扩散模型进行条件图像合成，其中条件可以表示为底层真实图像的已知函数。

实验

在本节中，我们展示了SDEdit在基于笔画的图像合成和编辑以及图像合成方面能够优于最先进的基于GAN的模型。SDEdit和基线方法都使用公开可用的预训练检查点。根据开源SDE检查点的可用性，我们在LSUN数据集上使用VP-SDE，在CelebA-HQ数据集上使用VE-SDE。

评价指标

我们基于真实感和忠实度评估编辑结果。为了量化真实感，我们使用生成图像与目标真实图像数据集之间的核插入评分（KID；详情见附录D.2），以及在Amazon Mechanical Turk（MTurk）上进行的不同方法之间的成对人类评估。为了量化忠实度，我们报告引导与编辑输出图像之间所有像素的$L_2$距离，并归一化到[0,1]。我们还在某些实验中考虑使用LPIPS（Zhang et al., 2018）和MTurk人类评估。为了量化总体人类满意度评分（真实感+忠实度），我们利用MTurk人类评估对基线方法和SDEdit进行成对比较（见附录F）。

基于笔画的图像合成

给定一个输入笔画绘画，我们的目标是在没有配对数据的情况下生成真实且忠实的图像。我们考虑由人类用户创建的笔画绘画引导（见图5）。同时，我们还提出了一种算法，基于源图像自动模拟用户笔画绘画，引导我们进行SDEdit的大规模定量评估。更多细节见附录D.2。

基线方法

为了比较，我们选择了三种最先进的基于GAN的图像编辑和合成方法作为我们的基线。我们的第一个基线是StyleGAN2-ADA（Karras et al., 2020a）中使用的图像投影方法，通过最小化感知损失在StyleGAN的W+空间中进行反演。我们的第二个基线是域内GAN（Zhu et al., 2020a），通过在编码器上运行优化步骤来实现反演。具体而言，我们考虑两种版本的域内GAN反演技术：第一种（记为域内GAN-1）仅使用编码器以最大化反演速度，第二种（记为域内GAN-2）运行额外的优化步骤以最大化反演准确性。我们的第三个基线是e4e（Tov et al., 2021），其编码器目标是通过鼓励将图像反演到预训练StyleGAN模型的W空间附近，在感知质量和可编辑性之间进行平衡。

结果

我们在图4中展示了定性比较结果。我们观察到所有基线方法都难以基于笔画绘画输入生成真实图像，而SDEdit成功生成了保留输入笔画绘画语义的真实图像。如图5所示，SDEdit还可以为同一输入合成多样化的图像。我们在表1中使用用户创建的笔画引导报告了定量比较结果，在表2中使用算法模拟的笔画引导报告了定量比较结果。我们报告$L_2$距离以进行忠实度比较，并利用MTurk（见附录F）或KID评分进行真实感比较。为了量化总体人类满意度评分（忠实度+真实感），我们要求不同的一组MTurk工作人员对基线方法和SDEdit进行另外3000次成对比较。我们观察到，SDEdit在所有评价指标上都优于基线方法，在真实感评分上超过基线方法80%以上，在总体满意度评分上超过基线方法75%以上。更多实验细节见附录C，更多结果见附录E。

灵活的图像编辑

在本节中，我们展示了SDEdit在图像编辑任务上能够优于现有的基于GAN的模型。我们专注于LSUN（卧室、教堂）和CelebA-HQ数据集，更多实验设置细节见附录D。

基于笔画的图像编辑

给定一个带有笔画编辑的图像，我们希望基于用户编辑生成一个真实且忠实的图像。我们考虑与之前实验相同的基于GAN的基线（Zhu et al., 2020a；Karras et al., 2020a；Tov et al., 2021）。如图6所示，基线生成的结果往往会引入不希望的修改，偶尔会使笔画外的

区域变得模糊。相比之下，SDEdit能够生成既真实又忠实于输入的图像编辑，同时避免了不希望的修改。附录E中提供了更多结果。

图像合成

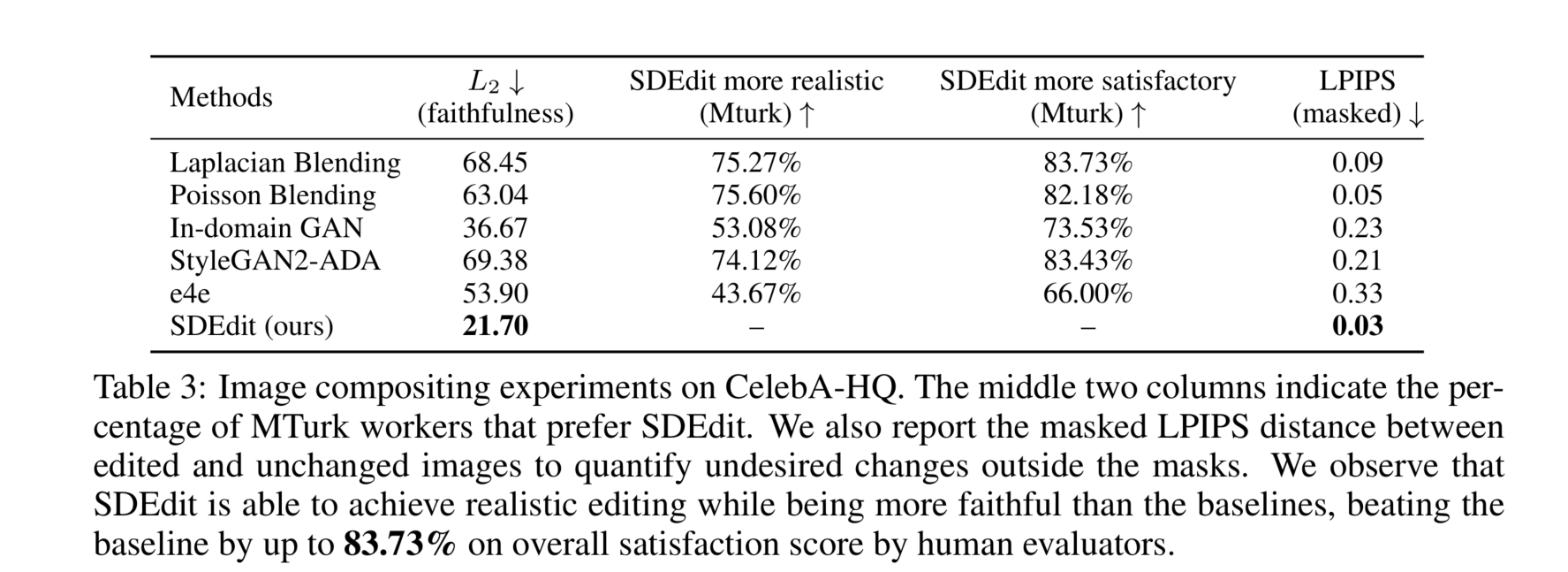
我们专注于在CelebA-HQ数据集（Karras et al., 2017）上的图像合成。给定一个从数据集中随机抽取的图像，我们要求用户指定他们希望编辑图像的样子，使用从其他参考图像复制的像素块以及他们希望进行修改的像素（见图7）。我们将我们的方法与传统的混合算法（Burt & Adelson, 1987；Pérez et al., 2003）和之前考虑的相同GAN基线进行比较。我们在图7中进行了定性比较。为了定量比较，我们报告了$L_2$距离以量化忠实度。为了量化真实感，我们要求MTurk工作人员对基线方法和SDEdit进行1500次成对比较。为了量化用户满意度评分（忠实度+真实感），我们要求不同的工作人员对SDEdit进行另外1500次成对比较。为了量化不希望的变化（例如身份变化），我们遵循Bau et al. (2020) 计算了掩码LPIPS（Zhang et al., 2018）。如表3所示，我们观察到SDEdit能够生成既忠实又真实的图像，其LPIPS评分远优于基线，在总体满意度评分上最多超过基线83.73%，在真实感上最多超过基线75.60%。尽管我们的真实感评分略低于e4e，但SDEdit生成的图像更加忠实且整体更令人满意。更多实验细节见附录D。

结论

我们提出了随机微分编辑（SDEdit），这是一种通过随机微分方程（SDEs）生成建模进行引导图像编辑和合成的方法，能够实现真实感和忠实度的平衡。与通过GAN反演的图像编辑技术不同，我们的方法不需要为重建输入设计特定任务的优化算法，特别适用于GAN反演损失难以设计或优化的数据集或任务。与条件GANs不同，我们的方法不需要为“引导”图像收集新数据集或重新训练模型，这两者都可能昂贵或耗时。我们证明了SDEdit在基于笔画的图像合成、基于笔画的图像编辑和图像合成方面优于现有的基于GAN的方法，而无需特定任务的训练。

这篇论文主要讲了通过随机微分方程（SDEs）进行图像合成和编辑的方法，即SDEdit。论文探讨了在没有特定任务训练的情况下，如何利用预训练的SDE模型生成既真实又忠实于用户输入的图像。以下是论文的主要内容概述：

1. 背景与挑战：

   • 传统的图像合成和编辑方法主要依赖于条件GAN和GAN反演，这些方法在平衡图像的真实感和对用户输入的忠实度方面存在挑战，并且通常需要大量的训练数据和复杂的损失函数设计。

2. SDEdit方法：

   • SDEdit利用扩散模型的生成先验，通过迭代去噪的方式生成逼真的图像。具体来说，给定用户输入（例如手绘笔画或图像编辑），SDEdit首先向输入添加噪声，然后通过逆向SDE逐步去除噪声，以生成既真实又忠实的图像。
   • 该方法不需要为每个新任务进行特定的训练或反演，能够自然地在真实感和忠实度之间找到平衡。

3. 实验与结果：

   • 论文通过一系列实验展示了SDEdit在基于笔画的图像合成和编辑以及图像合成任务中的优越表现。实验结果表明，SDEdit在真实感和忠实度方面均优于最先进的基于GAN的方法。
   • 例如，在LSUN数据集和CelebA-HQ数据集上的实验中，SDEdit在用户满意度评分上比基线方法高出80%以上。

4. 理论分析与算法：

   • 论文还提供了对SDEdit中关键参数（如$t_0$）的选择和调整的理论分析，说明了如何在真实感和忠实度之间进行权衡。
   • 提供了详细的算法步骤，并在附录中讨论了VP-SDE的详细算法和扩展。

5. 结论：

   • SDEdit方法在不需要特定任务训练的情况下，能够实现高效、灵活的图像编辑和合成，具有较广泛的应用前景。

总体来说，这篇论文提出了一种新颖且高效的图像合成与编辑方法，解决了现有方法中存在的一些主要问题，并在实验中展示了其优越性能。

添加噪声后，SD模型通过一种称为逆向随机微分方程（SDE）的过程逐步去除噪声，还原图像。这个过程可以分为以下几个步骤：

1. 添加高斯噪声：给定用户输入的引导图像$x^{(g)}$，在初始时间$t_0$向其添加高斯噪声，得到$x^{(g)}(t_0)$。这一步的公式如下：
   $$x^{(g)}(t_0)\sim N(x^{(g)};{\sigma }^2(t_0)I)$$
   其中，$\sigma (t_0)$表示噪声的标准差。

2. 初始化逆向SDE：使用添加噪声后的图像$x^{(g)}(t_0)$作为逆向SDE的初始状态。

3. 逆向SDE迭代去噪：通过逆向SDE从时间$t=t_0$迭代到$t=0$，逐步去除噪声，生成最终的图像$x(0)$。逆向SDE的具体公式为：
   $$dx(t)=\left(-\frac{d[{\sigma }^2(t)]}{dt}{\nabla }_x\log p_t(x)\right)dt+\sqrt{\frac{d[{\sigma }^2(t)]}{dt}}d\bar{w}$$
   其中，${\nabla }_x\log p_t(x)$是噪声扰动得分函数，$d\bar{w}$是维纳过程（Wiener process），即标准布朗运动。

4. 得分模型：得分函数${\nabla }_x\log p_t(x)$可以通过去噪得分匹配（denoising score matching）进行训练，记为$s_{\theta }(x(t),t)$。在训练阶段，学习目标为：
   $$L_t={\mathbb{E}}_{x(0)\sim p_{data},z\sim \mathcal{N}(0,I)}\left[{\Vert {\sigma }_t{s}_{\theta }(x(t),t)-z\Vert }_2^2\right]$$
   该目标用于训练一个参数化得分模型$s_{\theta }(x(t),t)$，以近似${\nabla }_x\log p_t(x)$。

5. Euler-Maruyama方法：在实际计算中，使用Euler-Maruyama方法来数值近似SDE的解。从时间$(t+\Delta t)$到$t$的更新规则为：
   $$x(t)=x(t+\Delta t)+({\sigma }^2(t)-{\sigma }^2(t+\Delta t))s_{\theta }(x(t),t)+\sqrt{{\sigma }^2(t)-{\sigma }^2(t+\Delta t)}z$$
   其中$z\sim \mathcal{N}(0,I)$。

通过上述步骤，SD模型能够有效地将添加噪声后的图像逐步去噪，恢复出既真实又忠实于原始引导图像的最终图像。这个过程依赖于逆向SDE和去噪得分匹配技术，使得模型在不需要特定任务训练的情况下，能够处理各种图像合成和编辑任务。