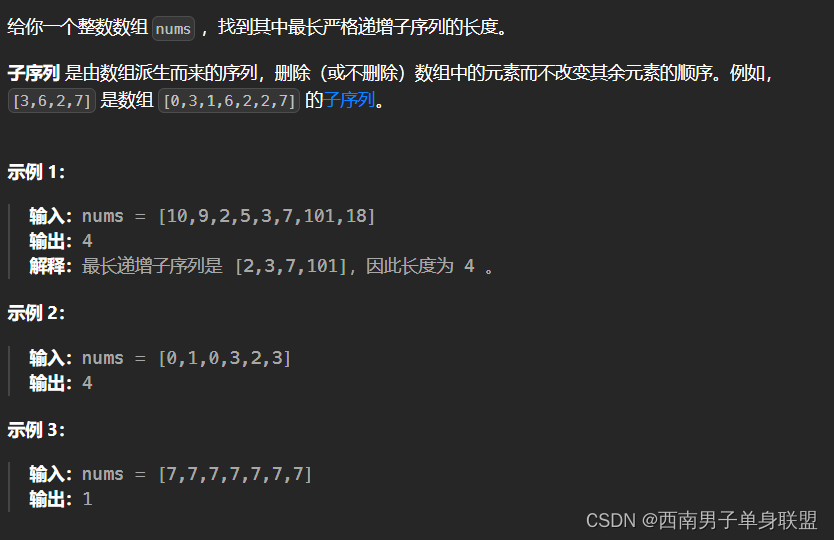
题干：

代码：

class Solution {
public:
    int lengthOfLIS(vector<int>& nums) {
        if(nums.size() <= 1)return nums.size();
        vector<int>dp(nums.size(), 1);
        int res = 0;
        for(int i = 1; i < nums.size(); i++){
            for(int j = 0; j < i; j++){
                if(nums[i] > nums[j]){
                    dp[i] = max(dp[j] + 1, dp[i]);
                }
            }
            if(dp[i] > res)res = dp[i];
        }
        return res;
    }
};

1.定义：dp[i]表示i之前包括i的以nums[i]结尾的最长递增子序列的长度

2.递推公式：

位置i的最长升序子序列等于j从0到i-1各个位置的最长升序子序列 + 1 的最大值。

所以：if (nums[i] > nums[j]) dp[i] = max(dp[i], dp[j] + 1);

注意这里不是要dp[i] 与 dp[j] + 1进行比较，而是我们要取dp[j] + 1的最大值，即：dp[i]为dp[j]+1的最大值，递推体现在由dp[j]+1推出dp[i]。

3.初始化：根据定义子序列一定不为空，所以都为1

4.遍历顺序：

dp[i] 是有0到i-1各个位置的最长递增子序列 推导而来，那么遍历i一定是从前向后遍历。

j其实就是遍历0到i-1，那么是从前到后。