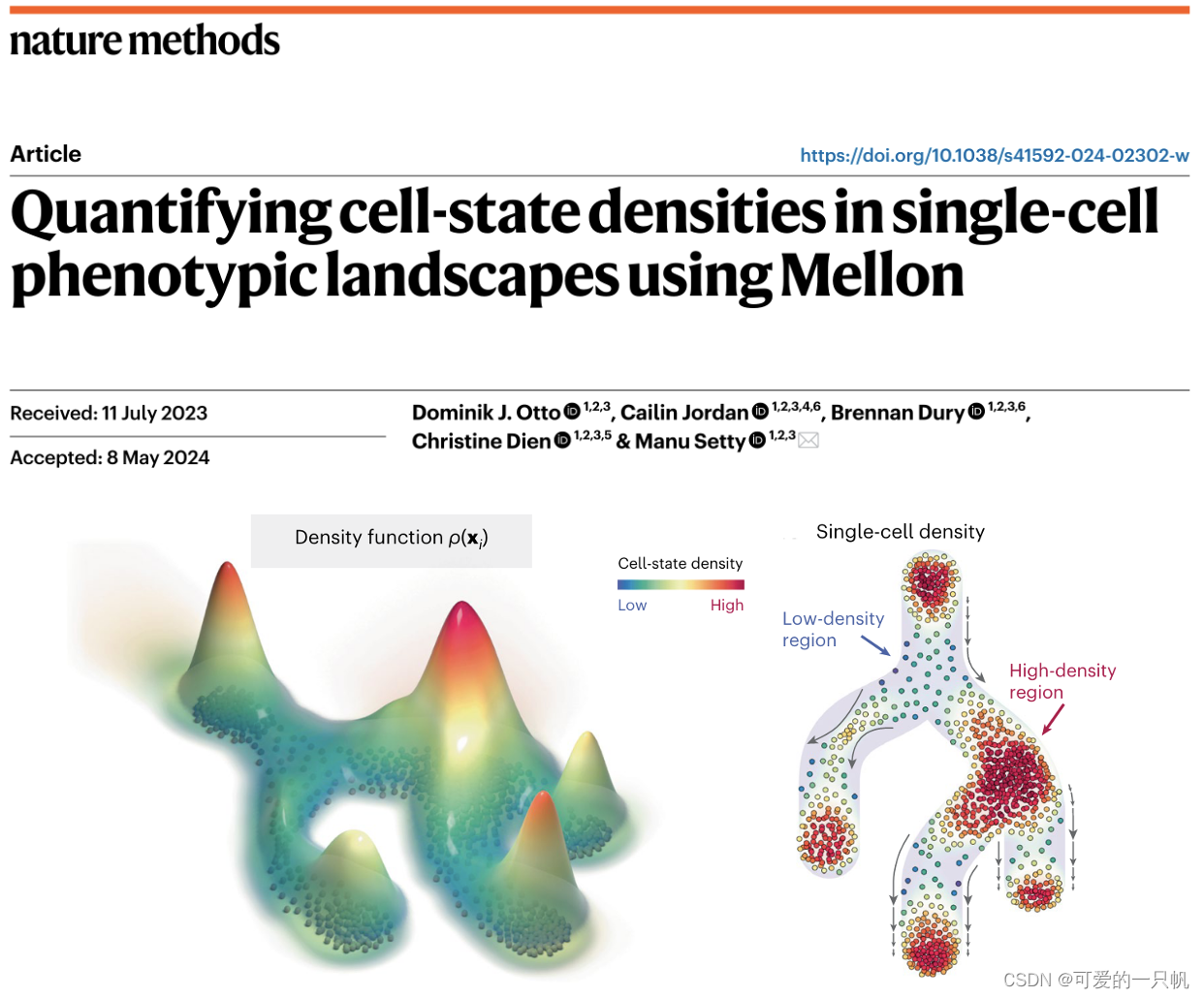
分化是支持所有多细胞生物发育和功能的动态过程。了解细胞如何沿着分化轨迹分布对解析驱动分化的机制、找出关键调控因素以及表征疾病中的失调至关重要。细胞状态密度是这种细胞分布的表现,受到基本生物过程的影响。增殖会增加某一状态下的细胞数目,从而提高细胞状态密度,而凋亡则降低细胞状态密度。细胞可能会聚集到检查点,导致高密度区域。相反,转录加速(如稀有的过渡性细胞)会导致低密度区域。因此,分化景观中的细胞状态密度可能并不均匀,而是表现出高低密度区域的丰富异质性。尽管细胞状态密度非常重要,但目前的单细胞数据高维密度估计算法通常产生噪声较大的结果,难以提供生物学上有意义的解释。
本文介绍了一种新算法Mellon,用于稳健地估计单细胞数据中的细胞状态密度。Mellon使用高维表示的细胞状态(如扩散图),依赖邻近距离和密度之间的内在关系,通过最近邻距离的分布与细胞状态密度相关联。然后,Mellon使用高斯过程连接高度相似的细胞状态之间的密度,计算出表征单细胞表型景观的细胞状态密度。与现有方法不同,Mellon推断出高维细胞状态空间中的连续密度函数,捕捉整个细胞群体的基本特征。该密度函数可用于确定单细胞分辨率的细胞状态密度。
Mellon旨在计算高维单细胞表型景观中的细胞状态密度,解决高维数据计算复杂性和低密度状态下的密度估计难题。
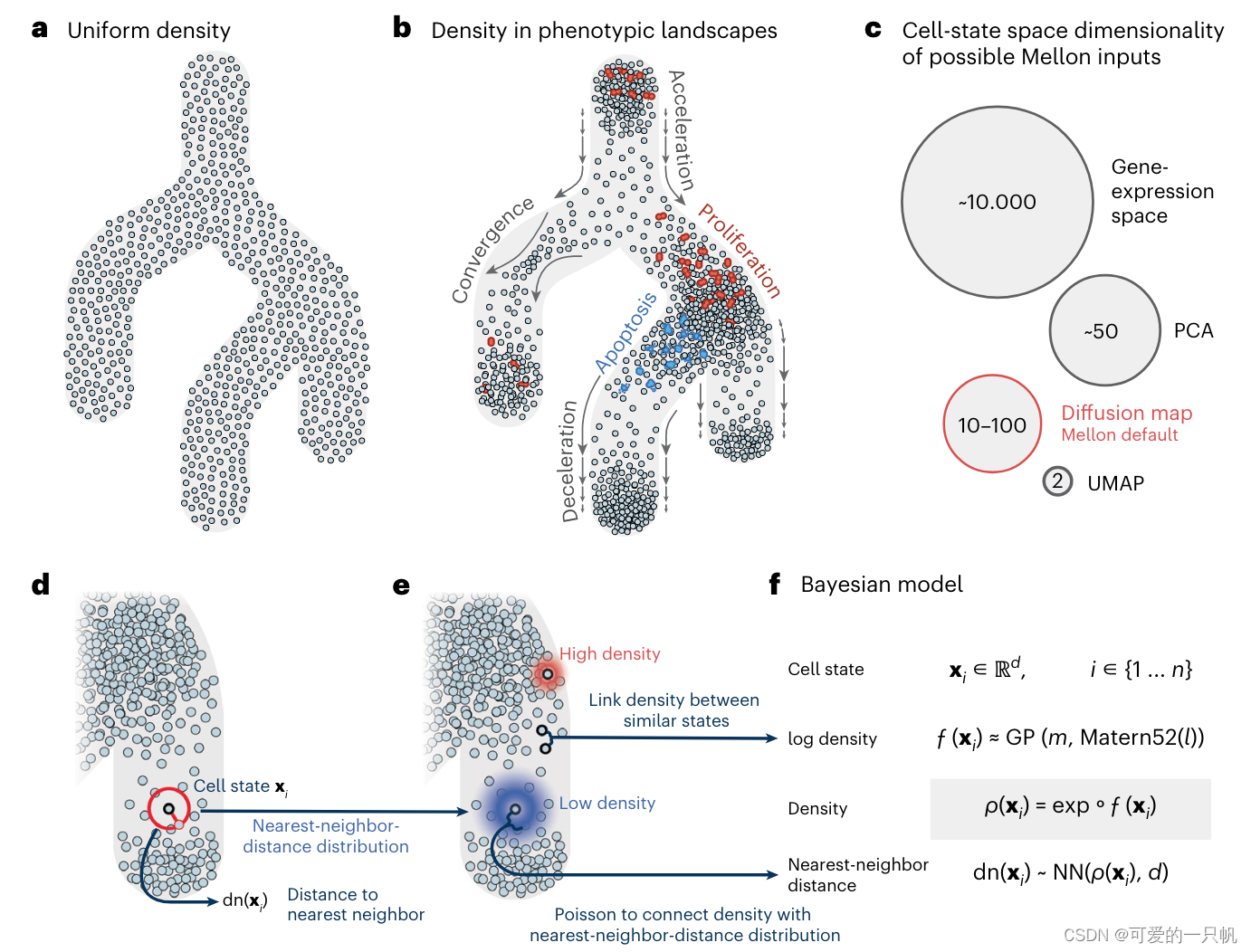
主要步骤:
1. 数据表示:使用扩散图(或其他降维技术如PCA)将细胞在高维表型空间中表示出来,每个点代表一个细胞状态。
2. 计算邻近距离:计算每个细胞在细胞状态空间中与其最近邻细胞之间的距离。
3. 密度估计:利用泊松点过程,通过邻近距离推断局部细胞密度。高密度区域对应较短的邻近距离,低密度区域对应较长的邻近距离。
4. 平滑密度函数:
• 高斯过程(GP):使用GP模型近似平滑的密度函数。GP通过协方差核函数编码细胞状态相似性,确保相关细胞之间的信息共享,从而生成连续的密度函数。
• 平滑过渡:假设细胞密度从一个状态到另一个状态是平滑且连续的,即相似细胞状态具有相似密度。
5. 贝叶斯推断:采用稀疏GP进行可扩展的贝叶斯推断,适用于大规模单细胞数据集。

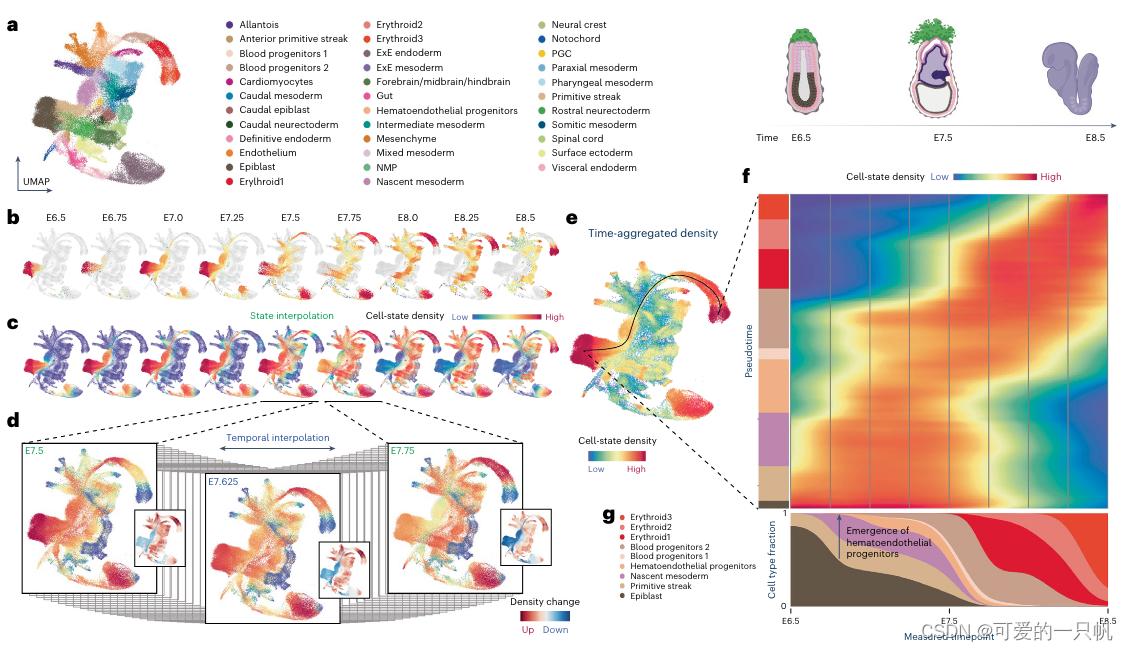 Mellon能够推断单细胞和染色质数据的密度,适用于不同的单细胞模式。
Mellon能够推断单细胞和染色质数据的密度,适用于不同的单细胞模式。
Mellon能够识别稀有且生物学上重要的细胞群体,揭示低密度区域中的快速转录变化由细胞自主和外部因素共同塑造。
在时间序列数据集中,Mellon通过构建时间连续的密度函数,提供了高分辨率的发育过程描绘,揭示了稀有过渡细胞状态和重要的发育转变。
这些发现展示了Mellon在揭示发育过程中的潜力,尤其是在识别和理解稀有转变细胞状态方面。
参考文献:Nature Methods, 2024, doi.org/10.1038/s41592-024-02302-w