一、ceres solver介绍

Ceres Solver 是一个开源的C++库，用于建模和解决大型、复杂的优化问题。它可以用来解决有边界约束的非线性最小二乘法问题和一般无约束的优化问题。

官网：http://www.ceres-solver.org/

案例网址：http://www.ceres-solver.org/tutorial.html

二、配置步骤

ceres需要eigen、ceres、gflags、glog、suitesparse三方库，编译过程比较复杂。下面介绍使用VS2019编译好的文件，来配置自己的工程。

2.1下载文件

文件下载链接：

原始工程与Include、Library、SharedDLL的位置为：

2.2配置环境

连接器：

debug下输入的静态文件：ceres-debug.lib glogd.lib

release下输入的静态文件：ceres.lib glog.lib

如果写相对路径，则为：

问题1：

ERROR macro is defined. Define GLOG_NO_ABBREVIATED_SEVERITIES before including logging.h. See the document for detail.

解决方案：

在预处理器中输入：GLOG_NO_ABBREVIATED_SEVERITIES

问题2：

The POSIX name for this item is deprecated. Instead, use the ISO C and C++ conformant name: _j1. See online help for details.

解决方案：

在预处理器中输入：_CRT_NONSTDC_NO_DEPRECATE

问题3：

“(”:“::”右边的非法标记

解决方案：

在预处理器中输入：NOMINMAX

问题4：

找不到ceres-debug.dll、glog.dll等动态链接

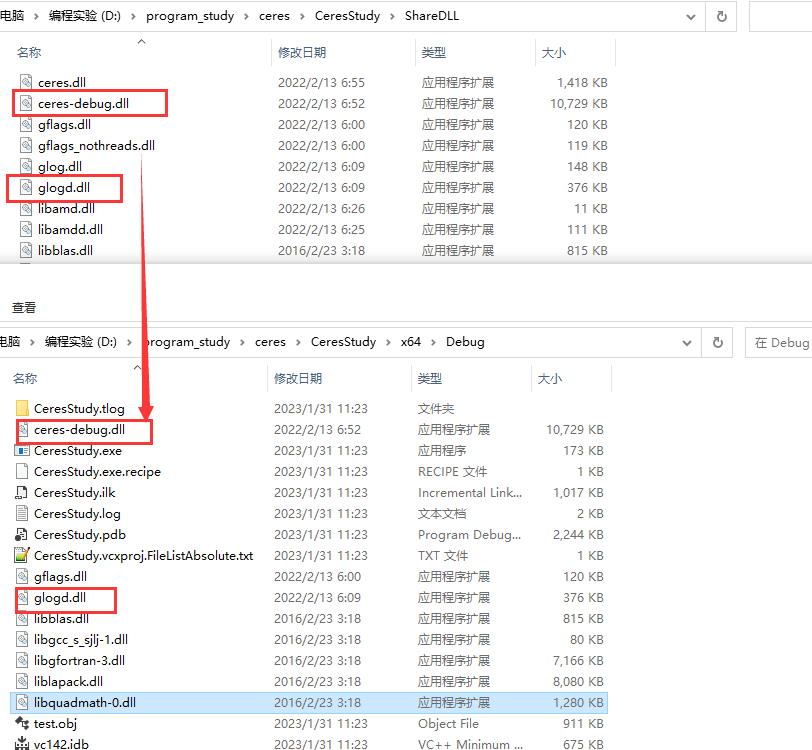
解决方案：

将ShareDLL中ceres-debug.dll、glogd.dll等动态链接文件复制到Debug文件夹下即可

三、测试

优化函数0.5(x-10)^2最小，其使用如下：

// Ceres Solver - A fast non-linear least squares minimizer
// Copyright 2015 Google Inc. All rights reserved.
// http://ceres-solver.org/
//
// Redistribution and use in source and binary forms, with or without
// modification, are permitted provided that the following conditions are met:
//
// * Redistributions of source code must retain the above copyright notice,
//   this list of conditions and the following disclaimer.
// * Redistributions in binary form must reproduce the above copyright notice,
//   this list of conditions and the following disclaimer in the documentation
//   and/or other materials provided with the distribution.
// * Neither the name of Google Inc. nor the names of its contributors may be
//   used to endorse or promote products derived from this software without
//   specific prior written permission.
//
// THIS SOFTWARE IS PROVIDED BY THE COPYRIGHT HOLDERS AND CONTRIBUTORS "AS IS"
// AND ANY EXPRESS OR IMPLIED WARRANTIES, INCLUDING, BUT NOT LIMITED TO, THE
// IMPLIED WARRANTIES OF MERCHANTABILITY AND FITNESS FOR A PARTICULAR PURPOSE
// ARE DISCLAIMED. IN NO EVENT SHALL THE COPYRIGHT OWNER OR CONTRIBUTORS BE
// LIABLE FOR ANY DIRECT, INDIRECT, INCIDENTAL, SPECIAL, EXEMPLARY, OR
// CONSEQUENTIAL DAMAGES (INCLUDING, BUT NOT LIMITED TO, PROCUREMENT OF
// SUBSTITUTE GOODS OR SERVICES; LOSS OF USE, DATA, OR PROFITS; OR BUSINESS
// INTERRUPTION) HOWEVER CAUSED AND ON ANY THEORY OF LIABILITY, WHETHER IN
// CONTRACT, STRICT LIABILITY, OR TORT (INCLUDING NEGLIGENCE OR OTHERWISE)
// ARISING IN ANY WAY OUT OF THE USE OF THIS SOFTWARE, EVEN IF ADVISED OF THE
// POSSIBILITY OF SUCH DAMAGE.
//
// Author: keir@google.com (Keir Mierle)
//
// A simple example of using the Ceres minimizer.
//
// Minimize 0.5 (10 - x)^2 using jacobian matrix computed using
// automatic differentiation.

#include "ceres/ceres.h"
#include "glog/logging.h"

using ceres::AutoDiffCostFunction;
using ceres::CostFunction;
using ceres::Problem;
using ceres::Solver;
using ceres::Solve;

// A templated cost functor that implements the residual r = 10 -
// x. The method operator() is templated so that we can then use an
// automatic differentiation wrapper around it to generate its
// derivatives.
struct CostFunctor {
    template <typename T> bool operator()(const T* const x, T* residual) const {
        residual[0] = T(10.0) - x[0];
        return true;
    }
};

int main(int argc, char** argv) {
    google::InitGoogleLogging(argv[0]);

    // The variable to solve for with its initial value. It will be
    // mutated in place by the solver.
    double x = 0.5;
    const double initial_x = x;

    // Build the problem.
    Problem problem;

    // Set up the only cost function (also known as residual). This uses
    // auto-differentiation to obtain the derivative (jacobian).
    CostFunction* cost_function =
        new AutoDiffCostFunction<CostFunctor, 1, 1>(new CostFunctor);
    problem.AddResidualBlock(cost_function, NULL, &x);

    // Run the solver!
    Solver::Options options;
    options.minimizer_progress_to_stdout = true;
    Solver::Summary summary;
    Solve(options, &problem, &summary);

    std::cout << summary.BriefReport() << "\n";
    std::cout << "x : " << initial_x
        << " -> " << x << "\n";
    system("pause");
    return 0;
}

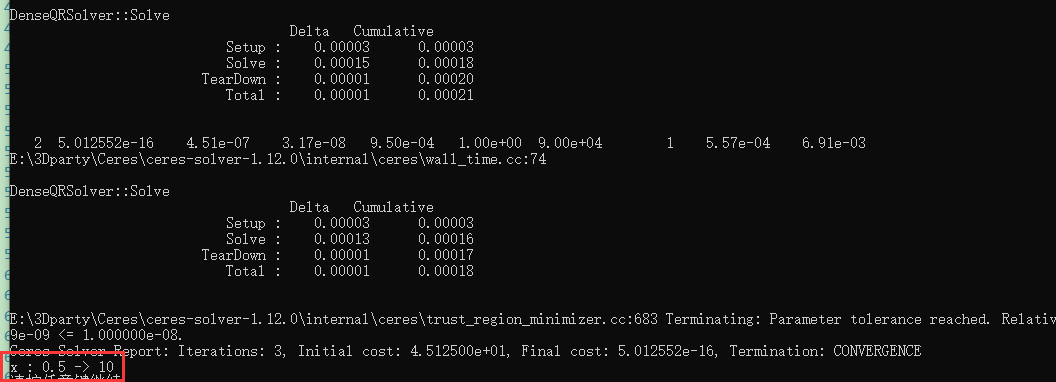
计算结果是：x=10时，最小为5.10*10^-10