目录
一.基本概念:
一.颜色分类:
二.排序数组:
三.数组中的第k个最大元素:
解法一:快速选择算法
解法二:简单粗暴优先级队列
四.库存管理Ⅲ:
解法一:快速选择
解法二:简单粗暴排序
解法三:简单粗暴优先级队列
一.基本概念:
🐻在计算机科学中,分治法是一种很重要的算法。字面上的解释就是“分而治之”,就是把一个复杂的问题分成两个或则更多个相同或相似的子问题,再把子问题分成更小的子问题……直到最后子问题可以简单的直接求解,原问题的解即子问题的解的合并。这个技巧是很多高效算法的基础,如排序算法(快速排序,归并排序),傅立叶变换(快速傅立叶变换)……
任何一个可以用计算机求解的问题所需的计算时间都与其规模有关。问题的规模越小,越容易直接求解,解题所需的计算时间也越少。例如,对于n个元素的排序问题,当n=1时,不需任何计算。n=2时,只要作一次比较即可排好序。n=3时只要作3次比较即可,…。而当n较大时,问题就不那么容易处理了。要想直接解决一个规模较大的问题,有时是相当困难的。🧐分治策略是:对于一个规模为n的问题,若该问题可以容易地解决(比如说规模n较小)则直接解决,否则将其分解为k个规模较小的子问题,这些子问题互相独立且与原问题形式相同,递归地解这些子问题,然后将各子问题的解合并得到原问题的解。这种算法设计策略叫做分治法。
当我们对分治算法有了以上的一定了解后,来练习几道题目加深理解~~
注(本文承接上文:分治精炼宝库----归并排序应用( ´◔︎ ‸◔︎`)_用分治法归并排序-CSDN博客)
一.颜色分类:
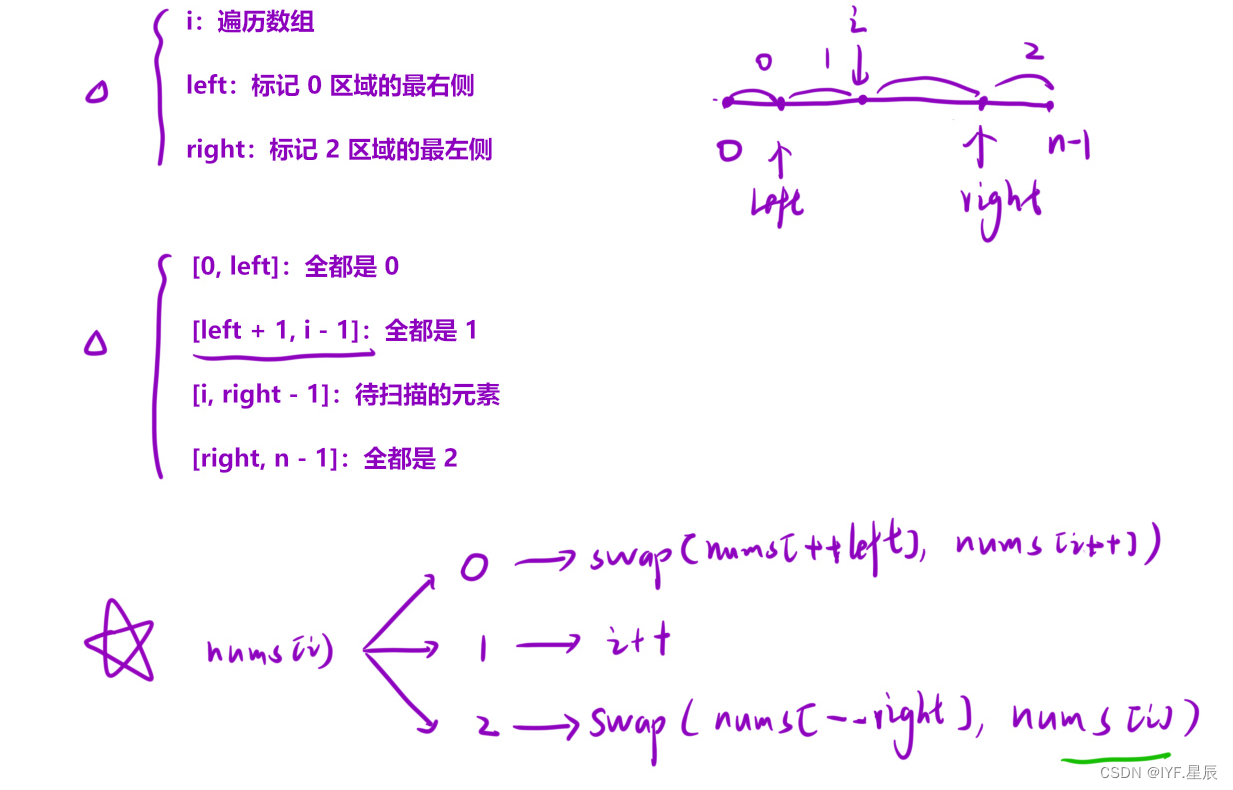
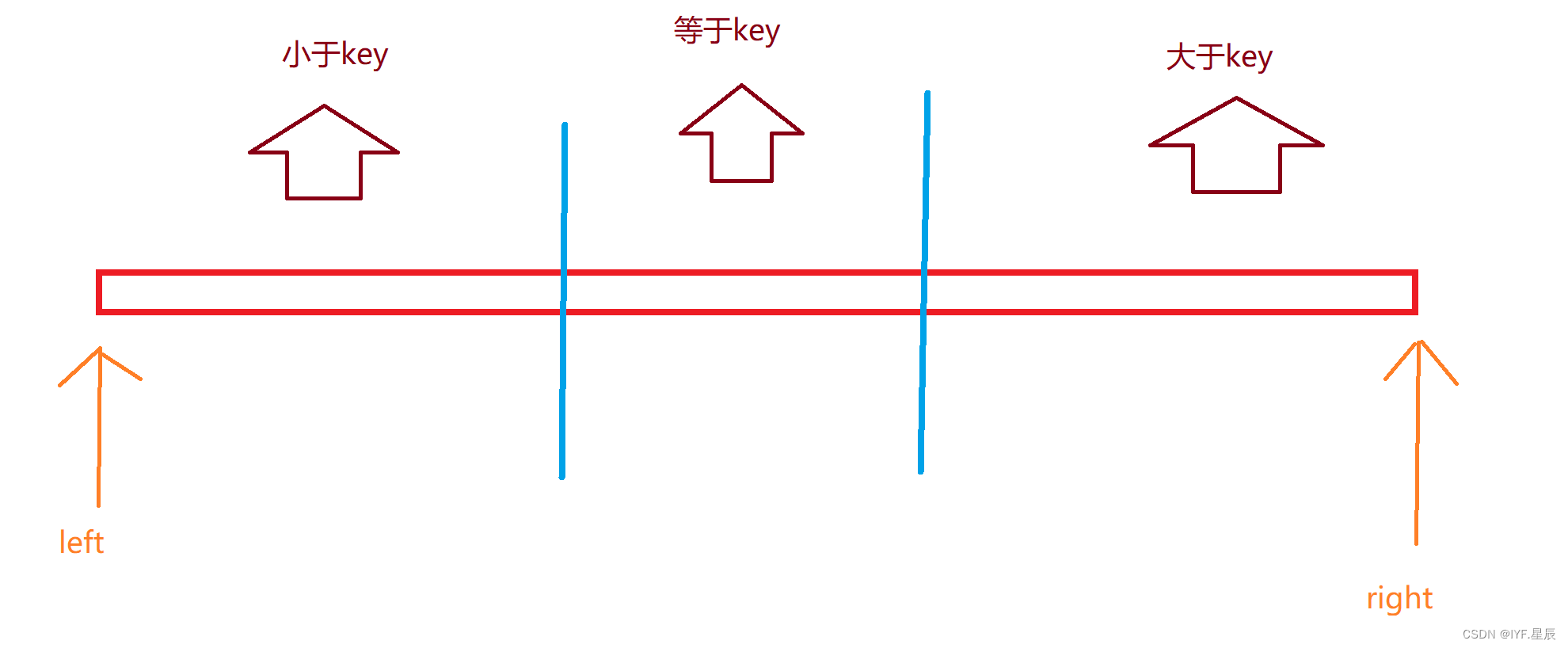
说明:这里我们用到的快速排序会使用数组分三块的思想(下文会详细说明),从数组中随机取一个元素key,将数组划分为三个区域,区域① < key ,区域 ② = key ,区域③ > key
题目链接:75. 颜色分类 - 力扣(LeetCode)

算法思路:
- 使用左指针left和右指针right来划分数组,初始时left为-1,right为数组长度n。
- 遍历数组nums,使用变量i作为当前遍历的索引。
- 如果nums[i]等于0,则将nums[i]与left+1位置的值交换,并将left和i都加1。
- 如果nums[i]等于1,则继续遍历下一个值。
- 如果nums[i]等于2,则将nums[i]与right-1位置的值交换,并将right和i都减1。
- 重复步骤4-6,直到遍历完成整个数组。
核心步骤:
代码详解:
class Solution {
public void sortColors(int[] nums) {
//将数组划分为三个区域[0,1,2]
int n = nums.length;
for(int i = 0,left = -1,right = n;i < right;){
if(nums[i] == 0){
swap(nums,++left,i++);
}else if(nums[i] == 1){
i++;
}else{
swap(nums,--right,i);
}
}
}
public void swap(int[] nums,int i,int j){
int tmp = nums[i];
nums[i] = nums[j];
nums[j] = tmp;
}
}运行结果:
二.排序数组:
题目链接:912. 排序数组 - 力扣(LeetCode)

这里我们使用快速排序来解决,首先,我们来一起看一下快速排序的核心框架:
void sort(int[] nums, int lo, int hi) {
if (lo >= hi) {
return;
}
// 对 nums[lo..hi] 进行切分
// 使得 nums[lo..p-1] <= nums[p] < nums[p+1..hi]
int p = partition(nums, lo, hi);
// 去左右子数组进行切分
sort(nums, lo, p - 1);
sort(nums, p + 1, hi);
}快速排序的核心即是先将一个元素排好序,再将剩下的元素排好序
快速排序的核心无疑是 partition 函数, partition 函数的作用是在 nums[lo..hi] 中寻找一个切分点 p,通过交换元素使得 nums[lo..p-1] 都小于等于 nums[p],且 nums[p+1..hi] 都大于 nums[p].
一个元素左边它小,右边都比它大,什么意思?不就是把它放到正确的排好序的位置上了吗?
所以 partition 函数干的事情,其实就是把 nums[p] 这个元素排好序了。
一个元素被排好序了,然后呢?你再把剩下的元素排好序不就行了嘛,排序图解:

其实我们不难发现,拍好序的数组就是一颗二叉搜索树!快速排序的过程其实也就是构造一棵二叉搜索树的过程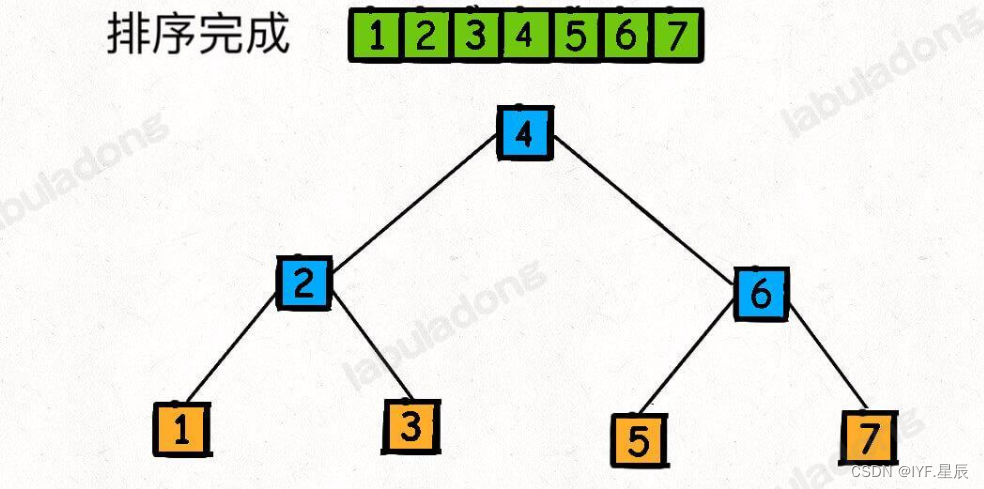
但谈到二叉搜索树的构造,那就不得不说二叉搜索树不平衡的极端情况,极端情况下二叉搜索树会退化成一个链表,导致操作效率大幅降低。这也和快速排序是一样的道理,特别是数组元素都相同的情况下,时间复杂度会大幅上升。
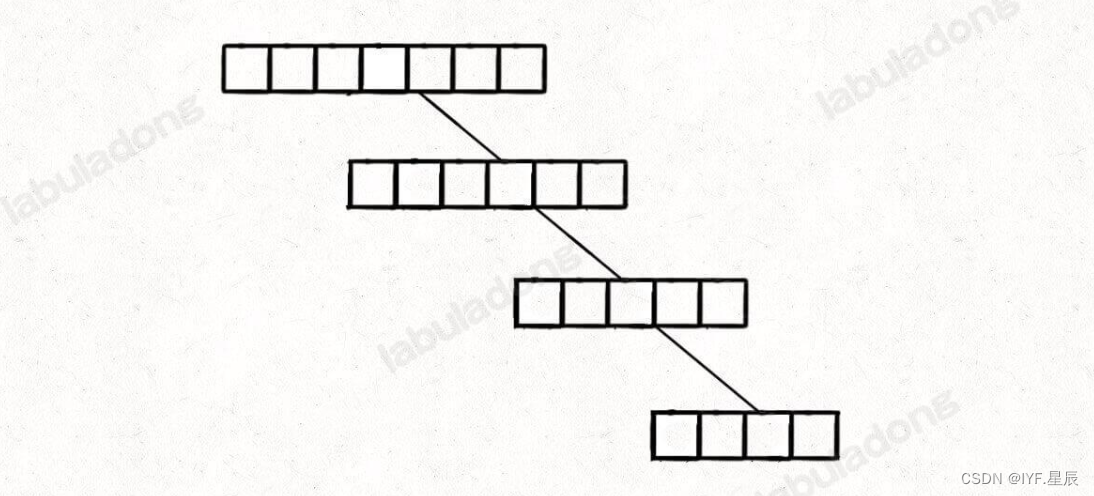
为了避免这种情况,我们要引入随机性:
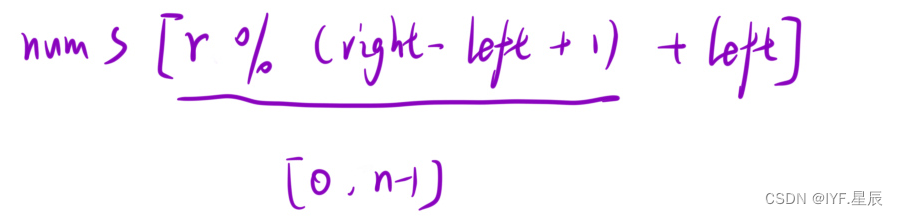
用代码表示就是(取left ~ right 区间的随机数,加上偏移量left):
int key = nums[new Random().nextInt(r - l + 1) + l];快排思路:
从数组中随机取一个元素key,将数组划分为三个区域,区域① < key ,区域 ② = key ,
区域③ > key,然后排序①区间和②区间即可
代码详解:
class Solution {
public int[] sortArray(int[] nums) {
quickSort(nums,0,nums.length - 1);
return nums;
}
public void quickSort(int[] nums,int l,int r){
if(l >= r) return ;
//设置一个随机数,然后将数组分为三块
int key = nums[new Random().nextInt(r - l + 1) + l];
int left = l - 1,cur = l,right = r + 1;
while(cur < right){
if(nums[cur] < key){
swap(nums,++left,cur++);
}else if(nums[cur] == key){
cur++;
}else{
swap(nums,--right,cur);
}
}
//在接着往后面找,此时数组区域[l,left] [left + 1,right - 1] [right,r]
quickSort(nums,l,left);
quickSort(nums,right,r);
}
public void swap(int[] nums,int i,int j){
int tmp = nums[i];
nums[i] = nums[j];
nums[j] = tmp;
}
}运行结果:
三.数组中的第k个最大元素:
题目链接:215. 数组中的第K个最大元素 - 力扣(LeetCode)

解法一:快速选择算法
思路:
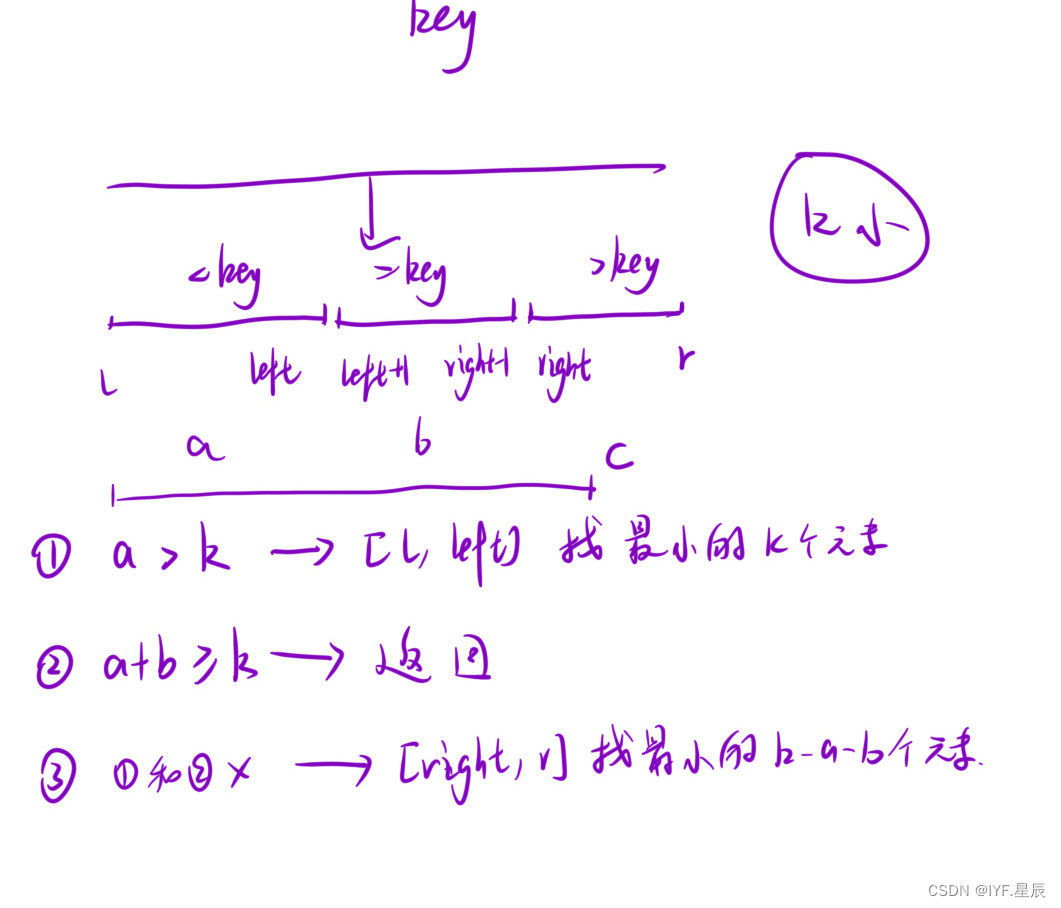
在快排中,当我们把数组「分成三块」之后: [l, left] [left + 1, right - 1] [right, r] ,我们可以通过计算每⼀个区间内元素的「个数」,进⽽推断出我们要找的元素是 在「哪⼀个区间」⾥⾯。那么我们可以直接去「相应的区间」去寻找最终结果就好了:
代码详解:
class Solution {
public int findKthLargest(int[] nums, int k) {
//快速选择算法,返回第k大的元素
int res = quickSort(nums,0,nums.length - 1,k);
return res;
}
public int quickSort(int[] nums,int l,int r,int k){
//当只有一个元素或则区间不存在时,直接返回
if(l >= r) return nums[l];
//数组分三块 [l,left][left + 1,right - 1][right,r]
int key = nums[new Random().nextInt(r - l + 1) + l];
int left = l - 1,cur = l,right = r + 1;
while(cur < right){
if(nums[cur] < key){
swap(nums,++left,cur++);
}else if(nums[cur] == key){
cur++;
}else{
swap(nums,--right,cur);
}
}
//分别对a b c 三个区间做判断,合适的区间
int b = right - left - 1,c = r - right + 1;
if(c >= k) return quickSort(nums,right,r,k);
else if(b + c >= k) return key;
//如果都不是,就去[l,left]区间找k - b - c大的元素
else return quickSort(nums,l,left,k - b - c);
}
public void swap(int[] nums,int i,int j){
int tmp = nums[i];
nums[i] = nums[j];
nums[j] = tmp;
}
}运行结果:
解法二:简单粗暴优先级队列
代码详解:
class Solution {
public int findKthLargest(int[] nums, int k) {
PriorityQueue<Integer> heap = new PriorityQueue<>((o1,o2)->{
return o2.compareTo(o1);
});
for(int i = 0;i < nums.length;i++){
heap.offer(nums[i]);
}
int res = 0;
for(int i = 0;i < k;i++){
res = heap.poll();
}
return res;
}
}运行结果:
四.库存管理Ⅲ:
题目链接:LCR 159. 库存管理 III - 力扣(LeetCode)

解法一:快速选择
思路:
在快排中,当我们把数组「分成三块」之后: [l, left] [left + 1, right - 1] [right, r] ,我们可以通过计算每⼀个区间内元素的「个数」,进⽽推断出最⼩的k个数在哪 些区间⾥⾯,那么我们可以直接去「相应的区间」继续划分数组即可:
代码详解:
class Solution {
public int[] inventoryManagement(int[] stock, int k) {
quickSort(stock,0,stock.length - 1,k);
int[] res = new int[k];
for(int i = 0;i < k;i++){
res[i] = stock[i];
}
return res;
}
public void quickSort(int[] nums,int l,int r,int k){
if(l >= r) return ;
//随机取数
int key = nums[new Random().nextInt(r - l + 1) + l];
int left = l - 1,cur = l,right = r + 1;
while(cur < right){
if(nums[cur] < key){
swap(nums,++left,cur++);
}else if(nums[cur] == key){
cur++;
}else{
swap(nums,--right,cur);
}
}
//寻找区间最小k个值[l,left] [left + 1,right - 1][right,r]
int a = left - l + 1,b = right - left - 1;
if(a > k) quickSort(nums,l,left,k);
else if(a + b >= k) return ;
else quickSort(nums,right,r,k - a - b);
}
public void swap(int[] nums,int i,int j){
int tmp = nums[i];
nums[i] = nums[j];
nums[j] = tmp;
}
}运行结果:

解法二:简单粗暴排序
代码详解:
class Solution {
public int[] inventoryManagement(int[] stock, int cnt) {
Arrays.sort(stock);
int[] res = new int[cnt];
for(int i = 0;i < cnt;i++){
res[i] = stock[i];
}
return res;
}
}运行结果:
解法三:简单粗暴优先级队列
代码详解:
class Solution {
public int[] inventoryManagement(int[] stock, int cnt) {
PriorityQueue<Integer> heap = new PriorityQueue<>();
for(int i = 0; i < stock.length; i++){
heap.offer(stock[i]);
}
int[] res = new int[cnt];
for(int i = 0;i < cnt;i++){
res[i] = heap.poll();
}
return res;
}
}参考资料:
五大常用算法之一:分治算法 - Will_Don - 博客园 (cnblogs.com)
《labuladong算法笔记》
封面来自:《hello 算法》
结语: 写博客不仅仅是为了分享学习经历,同时这也有利于我巩固知识点,总结该知识点,由于作者水平有限,对文章有任何问题的还请指出,接受大家的批评,让我改进。同时也希望读者们不吝啬你们的点赞+收藏+关注,你们的鼓励是我创作的最大动力!