九种查找算法-红黑树

news2024/11/15 4:33:26

红黑树

2-3查找树能保证在插入元素之后能保持树的平衡状态，最坏情况下即所有的子节点都是2-node，树的高度为lgn，从而保证了最坏情况下的时间复杂度。但是2-3树实现起来比较复杂，于是就有了一种简单实现2-3树的数据结构，即红黑树（Red-Black Tree）。

理解红黑树一句话就够了：红黑树就是用红链接表示3-结点的2-3树。

现在我们对2-3树进行改造，改造成一个二叉树。怎么改造呢？对于2节点，保持不变；对于3节点，我们首先将3节点中左侧的元素标记为红色，然后我们将其改造成图3的形式；

再将3节点的位于中间的子节点的父节点设置为父节点中那个红色的节点，如图4的所示；最后我们将图4的形式改为二叉树的样子，如图5所示。图5是不是很熟悉，没错，这就是我们常常提到的大名鼎鼎的红黑树了。如下图所示。

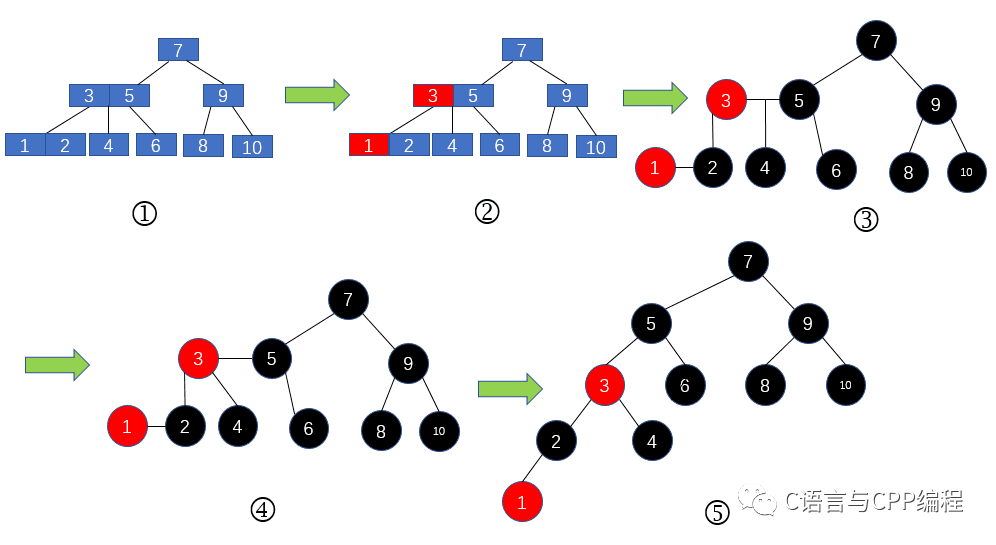
5b3fba6642e0e1235248bde563bf7bed.png

2-3树转红黑树

为什么使用红黑树：

  • 红黑树是一种平衡树，他复杂的定义和规则都是为了保证树的平衡性。如果树不保证他的平衡性就是下图：很显然这就变成一个链表了。

  • 保证平衡性的最大的目的就是降低树的高度，因为树的查找性能取决于树的高度。所以树的高度越低搜索的效率越高！

  • 这也是为什么存在二叉树、搜索二叉树等，各类树的目的。

红黑树性质：

  • 每个节点要么是黑色，要么是红色。

  • 根节点是黑色。

  • 每个叶子节点（NIL）是黑色。

  • 每个红色结点的两个子结点一定都是黑色。

  • 任意一结点到每个叶子结点的路径都包含数量相同的黑结点。

算法思路：

红黑树的思想就是对2-3查找树进行编码，尤其是对2-3查找树中的3-nodes节点添加额外的信息。红黑树中将节点之间的链接分为两种不同类型，红色链接，他用来链接两个2-nodes节点来表示一个3-nodes节点。黑色链接用来链接普通的2-3节点。特别的，使用红色链接的两个2-nodes来表示一个3-nodes节点，并且向左倾斜，即一个2-node是另一个2-node的左子节点。这种做法的好处是查找的时候不用做任何修改，和普通的二叉查找树相同。

代码：

#define BLACK 1
#define RED 0
#include <iostream>

using namespace std;

class bst
{
private:

	struct Node
	{
		int value;
		bool color;
		Node *leftTree, *rightTree, *parent;

		Node() : value(0), color(RED), leftTree(NULL), rightTree(NULL), parent(NULL) { }

		Node* grandparent()
		{
			if (parent == NULL)
			{
				return NULL;
			}
			return parent->parent;
		}

		Node* uncle()
		{
			if (grandparent() == NULL)
			{
				return NULL;
			}
			if (parent == grandparent()->rightTree)
				return grandparent()->leftTree;
			else
				return grandparent()->rightTree;
		}

		Node* sibling()
		{
			if (parent->leftTree == this)
				return parent->rightTree;
			else
				return parent->leftTree;
		}
	};

	void rotate_right(Node *p)
	{
		Node *gp = p->grandparent();
		Node *fa = p->parent;
		Node *y = p->rightTree;

		fa->leftTree = y;

		if (y != NIL)
			y->parent = fa;
		p->rightTree = fa;
		fa->parent = p;

		if (root == fa)
			root = p;
		p->parent = gp;

		if (gp != NULL)
		{
			if (gp->leftTree == fa)
				gp->leftTree = p;
			else
				gp->rightTree = p;
		}

	}

	void rotate_left(Node *p)
	{
		if (p->parent == NULL)
		{
			root = p;
			return;
		}
		Node *gp = p->grandparent();
		Node *fa = p->parent;
		Node *y = p->leftTree;

		fa->rightTree = y;

		if (y != NIL)
			y->parent = fa;
		p->leftTree = fa;
		fa->parent = p;

		if (root == fa)
			root = p;
		p->parent = gp;

		if (gp != NULL)
		{
			if (gp->leftTree == fa)
				gp->leftTree = p;
			else
				gp->rightTree = p;
		}
	}

	void inorder(Node *p)
	{
		if (p == NIL)
			return;

		if (p->leftTree)
			inorder(p->leftTree);

		cout << p->value << " ";

		if (p->rightTree)
			inorder(p->rightTree);
	}

	string outputColor(bool color)
	{
		return color ? "BLACK" : "RED";
	}

	Node* getSmallestChild(Node *p)
	{
		if (p->leftTree == NIL)
			return p;
		return getSmallestChild(p->leftTree);
	}

	bool delete_child(Node *p, int data)
	{
		if (p->value > data)
		{
			if (p->leftTree == NIL)
			{
				return false;
			}
			return delete_child(p->leftTree, data);
		}
		else if (p->value < data)
		{
			if (p->rightTree == NIL)
			{
				return false;
			}
			return delete_child(p->rightTree, data);
		}
		else if (p->value == data)
		{
			if (p->rightTree == NIL)
			{
				delete_one_child(p);
				return true;
			}
			Node *smallest = getSmallestChild(p->rightTree);
			swap(p->value, smallest->value);
			delete_one_child(smallest);

			return true;
		}
		else
		{
			return false;
		}
	}

	void delete_one_child(Node *p)
	{
		Node *child = p->leftTree == NIL ? p->rightTree : p->leftTree;
		if (p->parent == NULL && p->leftTree == NIL && p->rightTree == NIL)
		{
			p = NULL;
			root = p;
			return;
		}

		if (p->parent == NULL)
		{
			delete  p;
			child->parent = NULL;
			root = child;
			root->color = BLACK;
			return;
		}

		if (p->parent->leftTree == p)
		{
			p->parent->leftTree = child;
		}
		else
		{
			p->parent->rightTree = child;
		}
		child->parent = p->parent;

		if (p->color == BLACK)
		{
			if (child->color == RED)
			{
				child->color = BLACK;
			}
			else
				delete_case(child);
		}

		delete p;
	}

	void delete_case(Node *p)
	{
		if (p->parent == NULL)
		{
			p->color = BLACK;
			return;
		}
		if (p->sibling()->color == RED)
		{
			p->parent->color = RED;
			p->sibling()->color = BLACK;
			if (p == p->parent->leftTree)
				rotate_left(p->sibling());
			else
				rotate_right(p->sibling());
		}
		if (p->parent->color == BLACK && p->sibling()->color == BLACK
			&& p->sibling()->leftTree->color == BLACK && p->sibling()->rightTree->color == BLACK)
		{
			p->sibling()->color = RED;
			delete_case(p->parent);
		}
		else if (p->parent->color == RED && p->sibling()->color == BLACK
			&& p->sibling()->leftTree->color == BLACK && p->sibling()->rightTree->color == BLACK)
		{
			p->sibling()->color = RED;
			p->parent->color = BLACK;
		}
		else
		{
			if (p->sibling()->color == BLACK)
			{
				if (p == p->parent->leftTree && p->sibling()->leftTree->color == RED
					&& p->sibling()->rightTree->color == BLACK)
				{
					p->sibling()->color = RED;
					p->sibling()->leftTree->color = BLACK;
					rotate_right(p->sibling()->leftTree);
				}
				else if (p == p->parent->rightTree && p->sibling()->leftTree->color == BLACK
					&& p->sibling()->rightTree->color == RED)
				{
					p->sibling()->color = RED;
					p->sibling()->rightTree->color = BLACK;
					rotate_left(p->sibling()->rightTree);
				}
			}
			p->sibling()->color = p->parent->color;
			p->parent->color = BLACK;
			if (p == p->parent->leftTree)
			{
				p->sibling()->rightTree->color = BLACK;
				rotate_left(p->sibling());
			}
			else
			{
				p->sibling()->leftTree->color = BLACK;
				rotate_right(p->sibling());
			}
		}
	}

	void insert(Node *p, int data)
	{
		if (p->value >= data)
		{
			if (p->leftTree != NIL)
				insert(p->leftTree, data);
			else
			{
				Node *tmp = new Node();
				tmp->value = data;
				tmp->leftTree = tmp->rightTree = NIL;
				tmp->parent = p;
				p->leftTree = tmp;
				insert_case(tmp);
			}
		}
		else
		{
			if (p->rightTree != NIL)
				insert(p->rightTree, data);
			else
			{
				Node *tmp = new Node();
				tmp->value = data;
				tmp->leftTree = tmp->rightTree = NIL;
				tmp->parent = p;
				p->rightTree = tmp;
				insert_case(tmp);
			}
		}
	}

	void insert_case(Node *p)
	{
		if (p->parent == NULL)
		{
			root = p;
			p->color = BLACK;
			return;
		}
		if (p->parent->color == RED)
		{
			if (p->uncle()->color == RED)
			{
				p->parent->color = p->uncle()->color = BLACK;
				p->grandparent()->color = RED;
				insert_case(p->grandparent());
			}
			else
			{
				if (p->parent->rightTree == p && p->grandparent()->leftTree == p->parent)
				{
					rotate_left(p);
					rotate_right(p);
					p->color = BLACK;
					p->leftTree->color = p->rightTree->color = RED;
				}
				else if (p->parent->leftTree == p && p->grandparent()->rightTree == p->parent)
				{
					rotate_right(p);
					rotate_left(p);
					p->color = BLACK;
					p->leftTree->color = p->rightTree->color = RED;
				}
				else if (p->parent->leftTree == p && p->grandparent()->leftTree == p->parent)
				{
					p->parent->color = BLACK;
					p->grandparent()->color = RED;
					rotate_right(p->parent);
				}
				else if (p->parent->rightTree == p && p->grandparent()->rightTree == p->parent)
				{
					p->parent->color = BLACK;
					p->grandparent()->color = RED;
					rotate_left(p->parent);
				}
			}
		}
	}

	void DeleteTree(Node *p)
	{
		if (!p || p == NIL)
		{
			return;
		}
		DeleteTree(p->leftTree);
		DeleteTree(p->rightTree);
		delete p;
	}
public:

	bst()
	{
		NIL = new Node();
		NIL->color = BLACK;
		root = NULL;
	}

	~bst()
	{
		if (root)
			DeleteTree(root);
		delete NIL;
	}

	void inorder()
	{
		if (root == NULL)
			return;
		inorder(root);
		cout << endl;
	}

	void insert(int x)
	{
		if (root == NULL)
		{
			root = new Node();
			root->color = BLACK;
			root->leftTree = root->rightTree = NIL;
			root->value = x;
		}
		else
		{
			insert(root, x);
		}
	}

	bool delete_value(int data)
	{
		return delete_child(root, data);
	}
private:
	Node *root, *NIL;
};

int main()
{
	cout << "---【红黑树】---" << endl;
	// 创建红黑树
	bst tree;

	// 插入元素
	tree.insert(2);
	tree.insert(9);
	tree.insert(-10);
	tree.insert(0);
	tree.insert(33);
	tree.insert(-19);

	// 顺序打印红黑树
	cout << "插入元素后的红黑树：" << endl;
	tree.inorder();

	// 删除元素
	tree.delete_value(2);

	// 顺序打印红黑树
	cout << "删除元素 2 后的红黑树：" << endl;
	tree.inorder();

	// 析构
	tree.~bst();

	getchar();
	return 0;
}

 

 

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/188012.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

MySQL 数据库练习题记录02

MySQL 数据库练习题记录02

文章目录前言一、数据库基础1.1 sql练习题1.2 sql语句执行顺序1.3 sql语句编写前言 本文主要记录B站视频视频链接的内容&#xff0c;做到知识梳理和总结的作用&#xff0c;项目git地址。 一、数据库基础 1.1 sql练习题 user表数据: idusername1张三2李四3王五4小刘 user_r…
阅读更多...
代码随想录算法训练营第32天 回溯算法 java :491.递增子序列 46.全排列47.全排列 II

代码随想录算法训练营第32天 回溯算法 java :491.递增子序列 46.全排列47.全排列 II

文章目录LeetCode 491.递增子序列题目详解注意难点示意图LeetCode 46.全排列题目讲解难点LeetCode47.全排列 II题目讲解示图难点总结LeetCode 491.递增子序列 题目详解 注意难点 在题目中有涉及到 子集序列中至少有两个元素 可以用来进行判断 在单层遍历之前需要声明一个数组…
阅读更多...
统计学必备基础知识

统计学必备基础知识

一&#xff0c;统计学分为两种&#xff1a;1.描述性统计 2.推断性统计 1.统计数据的类型 (1).计量尺度分为3类&#xff1a;分类数据&#xff0c;顺序数据&#xff0c;数值型数据 分类数据&#xff1a;文字表达数据 顺序数据&#xff1a;非数据型数据&#xff0c;顺序数据…
阅读更多...
【swagger】spring security中 swagger2,swagger3和knife4j集成的区别 真的弄懂了吗?

【swagger】spring security中 swagger2,swagger3和knife4j集成的区别 真的弄懂了吗?

文章目录导包正确方式swagger2在security中放行swagger3在security中放行knife4j放行失败原因分析&#xff1a;swagger访问失败原因分析&#xff1a;作为一个强迫症重度的程序猿 不想多导一个jar包 本文创作背景是鉴于网上大多数是旧版本swagger2的教程&#xff0c;且没有针对2…
阅读更多...
【数据结构初阶】第五篇——栈和队列

【数据结构初阶】第五篇——栈和队列

栈 栈的概念及结构 栈的实现 栈的初始化 销毁栈 入栈 出栈 获取栈顶元素 检测栈是否为空 获取栈中有效元素个数 队列 队列的概念和结构 队列的实现 队列的初始化 销毁队列 入队 出队 获取对头元素 获取队尾元素 判断队列是否为空 获取队列中元素个数 栈 栈…
阅读更多...
13.包装类、正则表达式、Arrays类、常见算法、Lambda表达式

13.包装类、正则表达式、Arrays类、常见算法、Lambda表达式

目录 一.包装类 1.1 什么是包装类 1.2 包装类的作用 1.3 自动装箱和自动拆箱 1.3.1 自动装箱 1.3.2 自动拆箱 1.4 包装类的特有功能 二.正则表达式 2.1 什么是正则表达式 2.2 正则表达式的规定字符 2.3 字符串对象匹配正则表达式的方法 2.4 正则表达式在字符串方法中…
阅读更多...
21特征值和特征向量

21特征值和特征向量

特征值与特征向量初探 给定矩阵A&#xff0c;矩阵A乘以向量x&#xff0c;就像是使用矩阵A作用在向量x上&#xff0c;最后得到新的向量Ax。在这里&#xff0c;矩阵A就像是一个函数&#xff0c;接受一个向量x作为输入&#xff0c;给出向量Ax作为输出。 在这一过程中&#xff0c…
阅读更多...
算法基础集训（第29天）------＞DFS之排列数【DFS入门级算法，初学者必会】

算法基础集训（第29天）------＞DFS之排列数【DFS入门级算法，初学者必会】

一&#xff1a;概念定义该题对于排列数的定义是对给定的数字n&#xff0c;将从1~n的数字进行全排列并输出二&#xff1a;题目描述给定一个整数 n&#xff0c;将数字 1∼n 排成一排&#xff0c;将会有很多种排列方法。现在&#xff0c;请你按照字典序将所有的排列方法输出。输入…
阅读更多...
Java——只出现一次的数字(2)

Java——只出现一次的数字(2)

题目链接 leetcode在线oj题——只出现一次的数字(2) 题目描述 给你一个整数数组 nums &#xff0c;除某个元素仅出现 一次 外&#xff0c;其余每个元素都恰出现 三次 。请你找出并返回那个只出现了一次的元素。 你必须设计并实现线性时间复杂度的算法且不使用额外空间来解…
阅读更多...
Python对liunx中mysql数据库进行双表查询 10个案例带你了解

Python对liunx中mysql数据库进行双表查询 10个案例带你了解

关于Python连接liunx中mysql数据库的方式在这一篇文章 这里写目录标题1.在Liunx服务器中的mysql新建一个表2.插入数据3.连接liunx中的mysql数据库1、查询1946班的成绩信息2&#xff0c;查询1944班&#xff0c;语文成绩大于60小于90的成绩信息3&#xff0c;查询学生表中1到6行的…
阅读更多...
阿里国际站用户增长技术探索与实践

阿里国际站用户增长技术探索与实践

作者&#xff1a;阿里国际站用户增长团队 和众多传统行业一样&#xff0c;跨境贸易产业近年来也经历了数字化的转型创新&#xff0c;而首先参与进模式创新的地方主要集中于信息展示和业务撮合领域。本文将为大家分享阿里国际站在用户增长技术体系建设上的探索与实践。 一、跨境…
阅读更多...
SpringBoot超大文件上传（总结）

SpringBoot超大文件上传（总结）

SpringBoot超大文件上传&#xff0c;秒传&#xff01;分片上传!断电续传&#xff01;&#xff08;总结&#xff09;一. 秒传1、什么是秒传2、本文实现的秒传核心逻辑二. 分片上传1、什么是分片上传2、分片上传的场景三. 断点续传1、什么是断点续传2、应用场景3、实现断点续传的…
阅读更多...
【ESP32 WiFi篇（六）】ESP32 WebSocket

【ESP32 WiFi篇（六）】ESP32 WebSocket

文章目录1. WebSocket 概述2. WebSocket 的通信原理和机制3. WebSocket 与 HTTP 的关系3.1 相同点3.2 不同点3.3 关系4. WebSocket 技术出现之前&#xff0c;Web端实现即时通讯的方法有哪些&#xff1f;5. HTTP 存在的问题6. WebSocket 的特点7. WebSocket 数据帧格式1. WebSoc…
阅读更多...
简单局域网网络故障排查和处置

简单局域网网络故障排查和处置

简单局域网网络故障排查和处置一、了解基本网络构成1. IP传输通信图2.有线网络&#xff08;一&#xff09;物理层面&#xff08;1&#xff09;网线&#xff08;2&#xff09;网线的制作&#xff08;3&#xff09;网卡接口&#xff08;4&#xff09;光纤&#xff08;5&#xff0…
阅读更多...
【图像配准】使用OpenCV进行多图配准拼接

【图像配准】使用OpenCV进行多图配准拼接

本篇主要利用OpenCV自带的配准拼接函数Stitcher_create来实现多幅图像的配准拼接 代码参考自&#xff1a;https://github.com/samggggflynn/image-stitching-opencv 图像拼接创建步骤 通常来说&#xff0c;根据多个图像创建全景图的步骤为以下几步&#xff1a; 检测两张图像的…
阅读更多...
【pytest】三、pytest之setup和teardown，及封装

【pytest】三、pytest之setup和teardown，及封装

一、引言&#xff1a; 1&#xff09;setup的作用&#xff1a;用来实现执行前的一些初始化操作(如&#xff1a;数据准备、连接设备、打开APP/浏览器、创建日志对象、创建数据库连接、创建接口的请求对象等操作)&#xff1b; 2&#xff09;teardown的作用&#xff1a;用来实现执…
阅读更多...
C++学习/温习笔记：新型源码学编程（二）

C++学习/温习笔记：新型源码学编程（二）

写在前面 面向初学者撰写专栏&#xff0c;个人原创的学习C/C笔记&#xff08;干货&#xff09;编程练习所作源代码输出内容为中文&#xff0c;便于理解如有错误之处请各位读者指正请读者评论回复、参与投票&#xff0c;反馈给作者&#xff0c;我会获得持续更新笔记干货的动力。…
阅读更多...
放弃内卷，创造新市场

放弃内卷，创造新市场

在疫情&#xff0c;突然爆发的俄乌冲突&#xff0c;还有全球的物价上涨情况等社会问题逐渐变得尖锐的动荡中&#xff0c;让原本就不好的经济形势进入了寒冬期&#xff0c;各个行业也陆续进入了寒冬期&#xff0c;纷纷进入了内卷模式&#xff0c;尤其是对于跨境电商行业来说&…
阅读更多...
linux 部署jmeter报错处理

linux 部署jmeter报错处理

一、linux 安装jdk Java Downloads | Oracle 二、 linux上传jmeter 2.1 上传jmeter jmeter 下载地址&#xff1a; Apache JMeter - Download Apache JMeter 注意&#xff1a; 我先在我本地调试脚本&#xff08;mac环境&#xff09;&#xff0c;调试完成后&#xff0c;再在…
阅读更多...
java基于ssm的饰品商城的设计与实现

java基于ssm的饰品商城的设计与实现

管理员&#xff1b;管理员使用本系统涉到的功能主要有个人中心、用户管理、商品分类管理、商品信息管理、活动商品管理、知识普及管理、饰品圈、系统管理、订单管理等功能。 用户进入前台可以查看首页、商品信息、活动商品、知识普及、饰品圈、公告信息、个人中心、后台管理、购…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023