特征值与特征向量初探

给定矩阵A，矩阵A乘以向量x，就像是使用矩阵A作用在向量x上，最后得到新的向量Ax。在这里，矩阵A就像是一个函数，接受一个向量x作为输入，给出向量Ax作为输出。

在这一过程中，对一些特殊的向量很感兴趣，也即x和Ax始终保持同一个方向，这是比较特殊的，因为在大多情况下，Ax与x指向不同的方向。

在这种特殊的情况下，Ax平行于x，把满足这个条件的非零向量x称为A特征向量，而λ为A的特征值 。这个平行条件用方程表示就是：Ax = λx

对这个式子，我们试着计算特征值为0的特征向量，易得Ax = 0x = 0，因此，特征值为0的特征向量位于A的零空间中。显然对于奇异矩阵（不可逆），必然存在非零向量使得Ax = 0，所以若矩阵是奇异的，那么它有一个特征值为λ = 0。

• 先来看投影矩阵
  
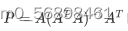
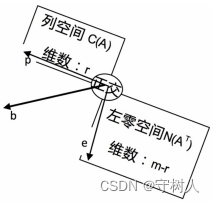
  （1） 用向量b乘以投影矩阵 P得到投影向量Pb，在这个过程中，只有当b本身已经处于投影平面（即A的列空间）中时，Pb才可能与b是同向的，此时b投影前后完全相同（Pb = 1 X b）。因此，投影平面（A 的列空间）中的所有向量都是投影矩阵的特征向量，且它们的特征值为1 。
  （2）再来观察投影平面的法向量，也即向量e。既然向量e与投影平面垂直，那么必然有Pe = 0，任何向量都与0向量是同向的。因此，投影平面的所有法向量（A的左零空间）也同样是投影矩阵的特征向量，且它们的特征值为0。
  综上可知，投影矩阵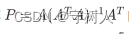
  的特征值λ = 1，0。

• 
  

求特征值和特征向量：Ax = λx

对于方程Ax = λx，有两个未知数，需要利用一些技巧从这一个方程中一次解出两个未知数（一个是特征值一个是特征向量），首先移项得（A - λI）x = 0。

观察新方程（A - λI）x = 0，右边的矩阵 λI 相当于将A矩阵平移了λ个单位，而如果新方程有非零解x（因为要求特征向量不可为零向量），则这个平移后的矩阵（A - λI）一定是奇异矩阵。

现在想要求的特征向量正是（A - λI）x = 0的非零解x，这就需要（A - λI）为奇异矩阵，结合行列式可得：

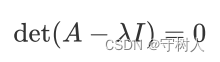
这样一来，方程中就没有x了， det（A - λI）也叫作特征方程。求解特征方程的带特征值λ，代回（A - λI）= 0，继续求（A - λI）的零空间即可。

• 举一个简单的例子，求解 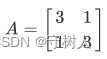的特征值与相应的特征向量。
  
  看转置矩阵A‘与本例中的对称矩阵A有什么联系。
  
  对于刚刚的例子，已经发现一次项系数似乎和矩阵的迹存在关系，更普遍地，能注意到矩阵的特征值之和等于矩阵的迹。同时如果我们计算矩阵A的行列式，能发现det（A） = 8 = λ1 X λ2 。下面给出两条有关矩阵特征值的性质：

• 矩阵的特征值之和等于矩阵的迹
  

• 矩阵的特征值之积等于矩阵的行列式
  

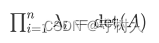
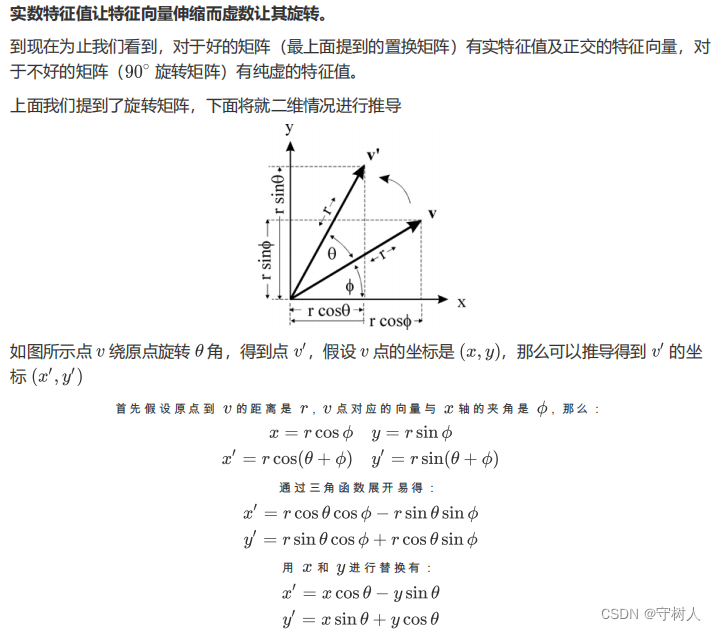
• 再来看旋转矩阵的例子，旋转90°的矩阵
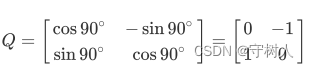
  （作用到向量上能将向量旋转90°，用Q表示旋转矩阵是因为旋转矩阵是正交矩阵中相当重要的例子）