LeetCode 491.递增子序列

题目详解

注意难点

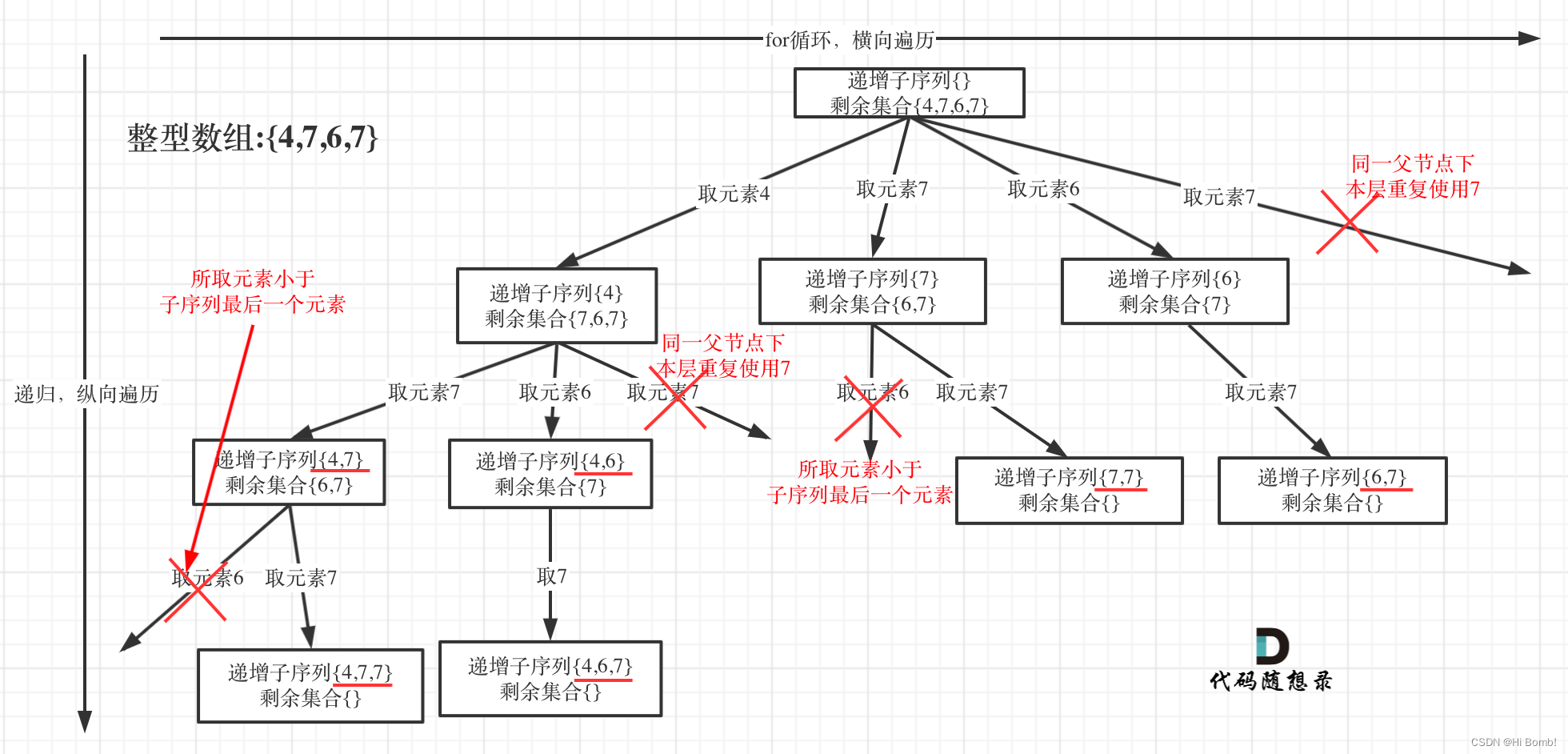
在题目中有涉及到子集序列中至少有两个元素可以用来进行判断
在单层遍历之前需要声明一个数组 used用来记录是否用过的记录如果使用过就是1 生命空间为201 因为题目中涉及到子集的选择范围会从-100 到正100 来看所以生命201

示意图

在这里插入图片描述

class Solution {
    List<List<Integer>> result = new ArrayList<>();
    LinkedList<Integer> path = new LinkedList();
    public List<List<Integer>> findSubsequences(int[] nums)   {
       backtrack( nums,0);
       return result;


    }
    public void backtrack(int nums[],int startIndex)
    {
        if( path.size()>1)
          {
              result.add(new ArrayList<>(path));
              
          }
        int [] used = new int[ 201];
        for(int i= startIndex;i<nums.length;i++)
        {
            if(!path.isEmpty()&& nums[i]< path.get(path.size()-1)|| used[nums[i]+100]==1)
            continue;
            used[nums[i]+100]=1;
            path.add(nums[i]);
            backtrack(nums,i+1);
            path.removeLast();
        }  
    }
}

LeetCode 46.全排列

题目讲解

难点

排列问题和组合问题大同小异最大的不同体现在单层遍历上面，因为组合上避免元素重复使用所以需要startIndex 来不停记录走到哪了而排列问题需要设置used数组来记录是否该元素已经调用即可

class Solution {
  List<List<Integer>> result = new ArrayList<>();// 存放符合条件结果的集合
    LinkedList<Integer> path = new LinkedList<>();// 用来存放符
    boolean [] used;
    public List<List<Integer>> permute(int[] nums) {
        used= new boolean[ nums.length]; 
        if(nums.length==0) return result;
        backtrack(nums);
        return result;
    }
    public void backtrack( int[] nums)
    {
        if(path.size()== nums.length)
        {
            result.add( new ArrayList<>( path));
            return;
        }
        for( int i=0;i<nums.length;i++)
        {
            if(used[i]) continue;
            used[i]=true;
            path.add(nums[i]);
            backtrack(nums);
            path.removeLast();
            used[i]= false;
        }
    }
}

LeetCode47.全排列 II

题目讲解

示图

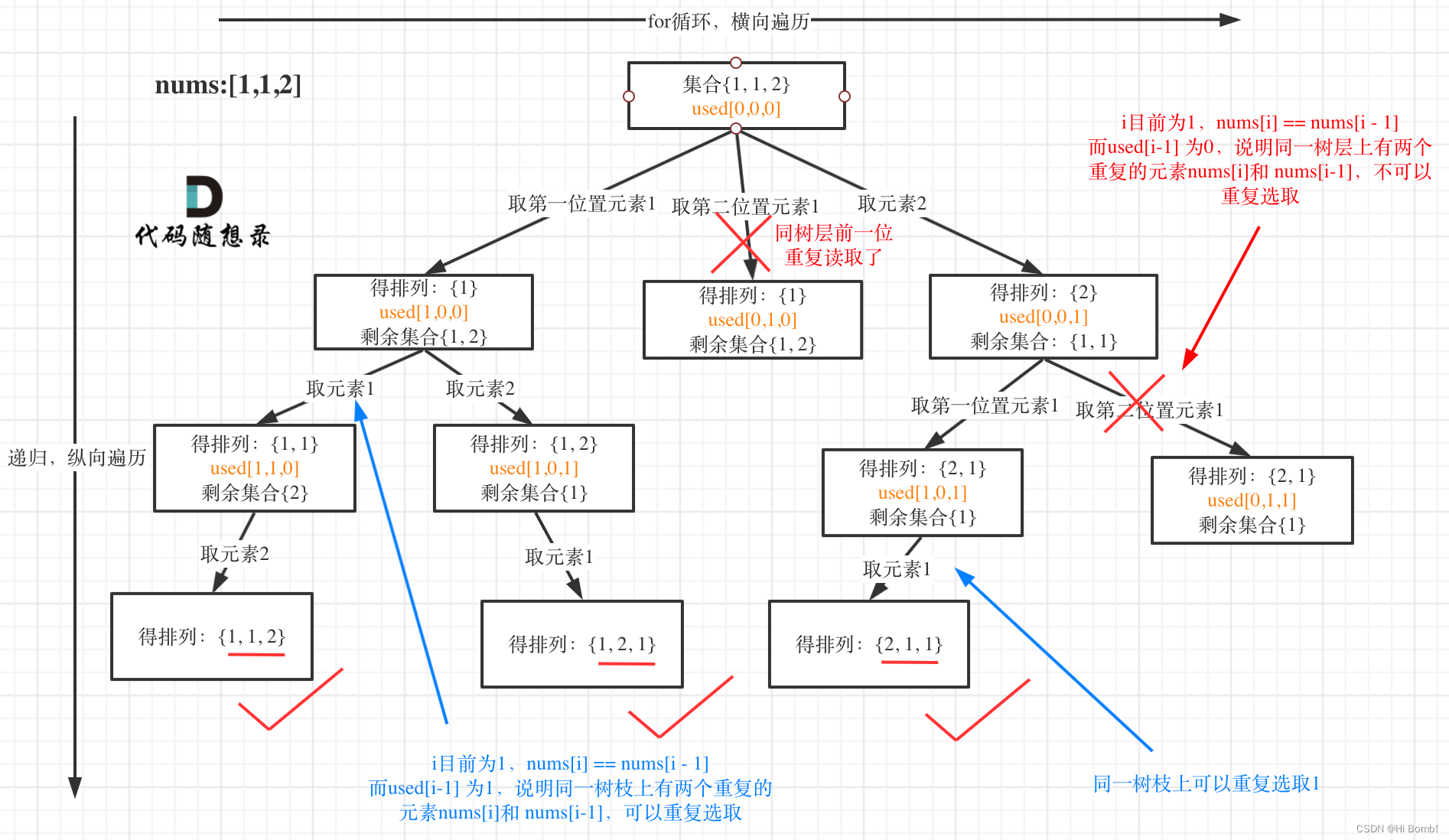
在这里插入图片描述

难点

在于如何进行去重因为给定的nums[ ]元素中有重复的所以在进行单层遍历的时候要进行剪枝操作
这里涉及到树枝去重和树层去重如果是树层去重，前面用过的，后面就不能用了。而树枝去重不必在意。因为数值去重会使用到相同的元素但是其实只是值相同而已。

class Solution {
    List<List<Integer>> result =new ArrayList<>();
    LinkedList<Integer> path = new LinkedList<>();
    public List<List<Integer>> permuteUnique(int[] nums) {
       Boolean[] used= new Boolean[nums.length];
       Arrays.fill(used,false);
       Arrays.sort( nums);
       backtrack( nums,used);
       return result;
    }
    public void backtrack(int[]nums, Boolean [] used)
    {
        if(path.size()== nums.length)
        {
            result.add(new ArrayList<>( path));
            return;
        }
        for(int i= 0;i< nums.length;i++)
        {
            if(i>0&& nums[i-1]==nums[i]&& used[i-1]== false)
            {continue;}
            if( used[i]==false)
            {
                used[i]= true;
                path.add(nums[i]);
                backtrack(nums,used);
                path.removeLast();
                used[i]= false;
            }
        }
    }
}