算法：链表

链表的技巧和操作总结

常用技巧：

链表中的常用操作

题目一：反转一个单链表

题目二：链表的中间结点

题目三：返回倒数第k个结点

题目四：合并两个有序链表

题目五：移除链表元素

题目六：链表分割

题目七：链表的回文结构

题目八：相交链表

题目九：环形链表I环形链表I

题目十：环形链表II

题目十一：随机链表的复制

题目十二：两数相加

题目十三：两两交换链表中的结点

题目十四：重排链表

题目十五：合并 k 个升序链表

题目十六：K 个一组翻转链表

链表的技巧和操作总结

常用技巧：

画图

能画图就画图，直观形象，比较容易我们理解

引入虚拟头结点

因为题目中，大多数都是第一个节点就存储的是有效元素了，这时就需要考虑许多的边界情况，比较麻烦，所以我们可以引入一个虚拟的头结点，即变为了带哨兵位头结点的链表

①便于我们处理边界条件
②方便我们对链表进行操作

不吝啬空间，大胆定义变量

例如有题是在A和B节点之间插入一个新结点C，此时按照往常的思维，会考虑先执行哪一步，才不会影响后面的操作，因为如果顺序执行错了，可能就找不到A后面的B结点了

那么这时，我们可以在操作前，提前定义一个变量next，让它代表B结点，这样无论我们怎么操作，都不会导致执行这步操作时，造成找不到B结点的情况

快慢双指针

快慢双指针，非常适合于判断链表中是否有环、找链表中环的入口、找链表中倒数第n个结点

下面的前几道题中，就有快慢双指针的方式解决的题目

链表中的常用操作

①创建一个新结点

②尾插

③头插（逆序链表）

在进行题目练习之前，需要知道，题目中所给的链表，每一个结点的结构都是如下所示的，直接使用即可：

struct ListNode 
{
    int val;
    ListNode *next;
    ListNode() : val(0), next(nullptr) {}
    ListNode(int x) : val(x), next(nullptr) {}
    ListNode(int x, ListNode *next) : val(x), next(next) {}
};

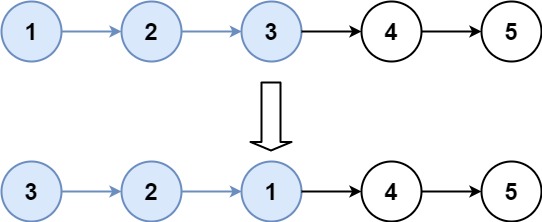
题目一：反转一个单链表

给你单链表的头节点 head ，请你反转链表，并返回反转后的链表。

示例 1：

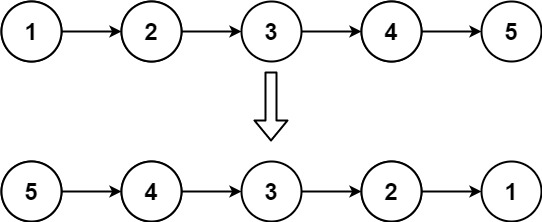
输入：head = [1,2,3,4,5]
输出：[5,4,3,2,1]

示例 2：

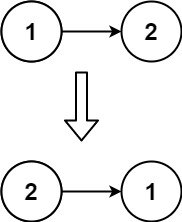
输入：head = [1,2]
输出：[2,1]

示例 3：

输入：head = []
输出：[]

解法一：头插法

这里的反转单链表是非常经典的头插就可以解决问题，这里可以使用哨兵位头结点也可以不使用，一般尾插时用哨兵位头结点的情况比较多，头插可以不用，具体看下面说明：

初始我们可以将head赋值给cur，再创建一个newhead的结点指针，为了防止将cur头插到newhead后面时找不到原链表cur后面的结点了，所以还需要创建一个next的指针，指向cur后面的结点，初始情况如下：

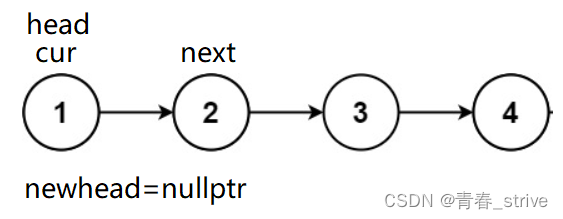
所以接下来头插的操作就是
创建next保存cur->next，cur->next = newhead，newhead = cur，cur = next，变为下图的情况：

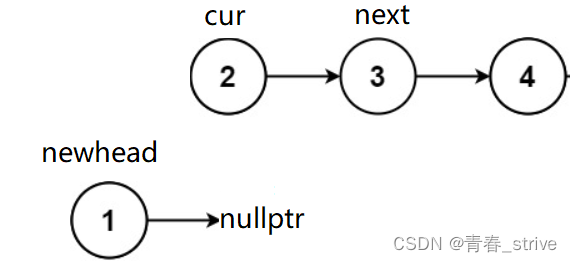
接下来依旧是进行上述操作：

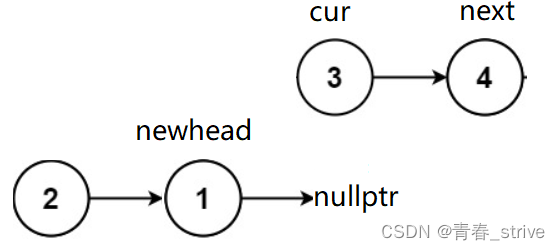
以此类推...

不带哨兵位的头结点的代码如下：

class Solution {
public:
    ListNode* reverseList(ListNode* head) 
    {
        ListNode* cur = head;
        ListNode* newhead = nullptr;
        while(cur)
        {
            ListNode* next = cur->next;//保存cur->next
            cur->next = newhead;
            newhead = cur;
            cur = next;
        }
        return newhead;
    }
};

带哨兵位的头结点就不细说了，代码如下：

class Solution {
public:
    ListNode* reverseList(ListNode* head) 
    {
        ListNode* cur = head;
        ListNode* tail = new ListNode;//哨兵位头结点tail
        tail->next = nullptr;
        while(cur)
        {
            ListNode* next = cur->next;
            cur->next = tail->next;
            tail->next = cur;
            cur = next;
        }
        ListNode* del = tail;
        tail = tail->next;
        delete del;//释放new出来的哨兵位头结点
        return tail;
    }
};

解法二：指针的方向颠倒

指针方向颠倒的思想，如下所示：

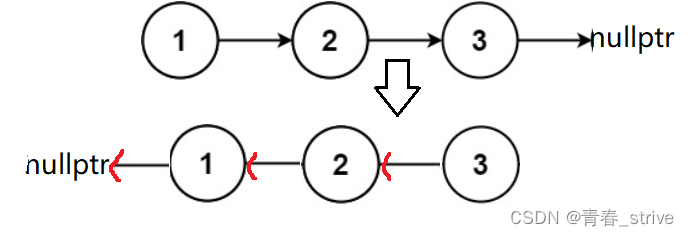
最后返回val为3的结点指针即可，那么如何定义变量呢

首先需要一个cur指针指向当前的结点，需要一个prev指针指向前一个结点，便于方向指向，最后还需要一个next指针，指向cur之后的结点，避免找不到cur后面的结点

初始指向是这样的：

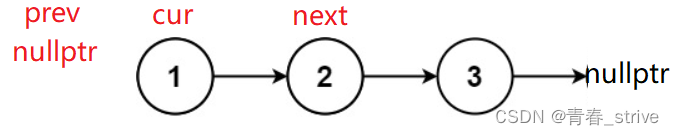
需要先记录cur的下一个结点next，再将cur指向prev，改变prev的指向到cur，再移动cur到next：

知道cur指向nullptr为止，此时位置信息如下：

此时返回prev即可

代码如下：

class Solution {
public:
    ListNode* reverseList(ListNode* head) 
    {
        ListNode* cur = head;
        ListNode* prev = nullptr;
        while(cur)
        {
            ListNode* next = cur->next;//定义cur的下一个结点位置
            cur->next = prev; //指针颠倒
            prev = cur; //改变prev指向
            cur = next; //改变cur位置
        }
        return prev;
    }
};

题目二：链表的中间结点

给你单链表的头结点 head ，请你找出并返回链表的中间结点。

如果有两个中间结点，则返回第二个中间结点。

示例 1：

输入：head = [1,2,3,4,5]
输出：[3,4,5]
解释：链表只有一个中间结点，值为 3 。

示例 2：

输入：head = [1,2,3,4,5,6]
输出：[4,5,6]
解释：该链表有两个中间结点，值分别为 3 和 4 ，返回第二个结点。

解法一：遍历求个数

这道题就很典型了，有很多种解法，最简单的就是先遍历一遍得到链表的元素个数，除2得到该链表第几个位置是中间数，然后第二次遍历，遍历到该结点时就return即可

代码如下：

class Solution 
{
public:
    ListNode* middleNode(ListNode* head) 
    {
        ListNode* cur = head;
        int num = 0;
        while(cur)
        {
            num++;
            cur = cur->next;
        }
        int mid = num / 2 + 1;//得到中间值，不论奇数还是偶数个都适用
        cur = head;
        while(--mid)//--mid循环mid-1次，因为cur刚开始就指向第一个位置
        {
            cur = cur->next;
        }
        return cur;
    }
};

解法二：快慢指针

这道题就是典型的可以使用快慢指针的思想，定义两个指针，一个slow一个fast

慢指针slow一次走一步，快指针fast一次走两步，当快指针走到链表的结尾时，慢指针自然走到中间位置了

下面举奇数个的例子，奇数个时判断条件是fast->next为空：

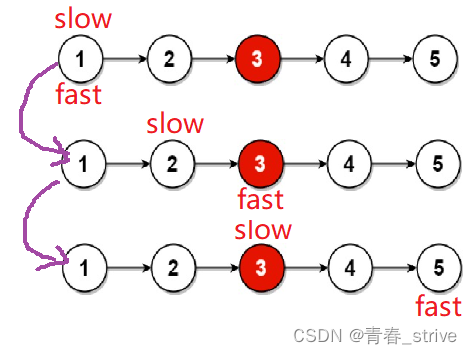
下面是偶数个的例子，偶数个时判断条件是fast为空：

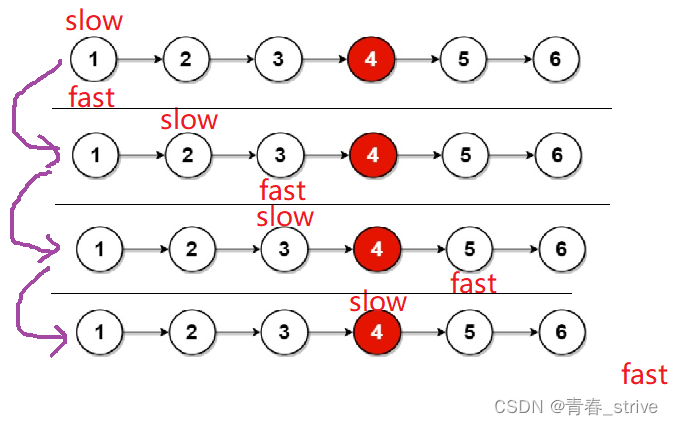
这种快慢指针的方法，无论奇数个还是偶数个都能够满足题目要求

代码如下：

class Solution 
{
public:
    ListNode* middleNode(ListNode* head) 
    {
        ListNode* slow, *fast;
        slow = fast = head;
        while(fast && fast->next)
        {
            slow = slow->next;
            fast = fast->next->next;
        }
        return slow;
    }
};

题目三：返回倒数第k个结点

实现一种算法，找出单向链表中倒数第 k 个节点。返回该节点的值。

示例：

输入： 1->2->3->4->5 和 k = 2
输出： 4

说明：

给定的 k 保证是有效的。

解法一：求链表的长度

解法一依旧是求链表的长度num，题目要求是倒数第k个，所以找正数的第num-k+1个，这种方式比较简单，就不写代码了

解法二：快慢指针

这道题的快慢指针就与之前的快慢指针思路略有不同，因为求的是倒数第k个，那么我的快慢指针之间可以先隔k个结点，接着快慢指针一起移动，直到快指针指向空为止，此时慢指针的位置就是倒数第k个结点，因为快指针指向空了，快慢指针之间刚好隔了k个结点，所以return慢指针的位置即可

代码如下：

class Solution {
public:
    int kthToLast(ListNode* head, int k) 
    {
        ListNode *fast, *slow;
        fast = slow = head;
        while(k--) fast = fast->next;//快指针先走k步
        while(fast)
        {
            slow = slow->next;
            fast = fast->next;
        }
        return slow->val;
    }
};

题目四：合并两个有序链表

将两个升序链表合并为一个新的升序链表并返回。新链表是通过拼接给定的两个链表的所有节点组成的。

示例 1：

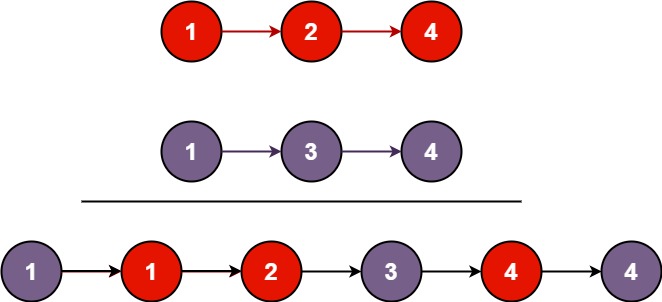
输入：l1 = [1,2,4], l2 = [1,3,4]
输出：[1,1,2,3,4,4]

示例 2：

输入：l1 = [], l2 = []
输出：[]

示例 3：

输入：l1 = [], l2 = [0]
输出：[0]

解法：取两个链表中较小的尾插到新链表中

对于新链表，既可以给哨兵位头结点，也可以不给，如果有哨兵位的头结点可以不用判断是否是第一次尾插，也不会有一些空指针的问题，比较简单，所以下面就以带哨兵位头结点为例：

所以先创建哨兵位的头结点，赋值给newhead和tail

再进行while循环，判断条件是(list1 && list2)，表示有一个链表为空就停止循环

接着判断哪一个链表还有结点，就将tail->next指向该链表，到此成功将list1和list2的结点，按照从小到大的顺序尾插到新链表中，最后还需将创建的哨兵位头结点delete掉即可

代码如下：

class Solution {
public:
    ListNode* mergeTwoLists(ListNode* list1, ListNode* list2) 
    {
        ListNode* newhead, *tail;
        newhead = tail = new ListNode;//哨兵位头结点
        while(list1 && list2)//尾插小的那一个结点
        {
            if(list1->val <= list2->val)
            {
                tail->next = list1;
                tail = tail->next;
                list1 = list1->next;
            }
            else
            {
                tail->next = list2;
                tail = tail->next;
                list2 = list2->next;
            }
        }
        //将还有剩余元素的链表尾插到新链表后面
        if(list1) tail->next = list1;
        if(list2) tail->next = list2;
        ListNode* head = newhead->next;
        delete newhead; //释放哨兵位头结点
        return head;
    }
};

题目五：移除链表元素

给你一个链表的头节点 head 和一个整数 val ，请你删除链表中所有满足 Node.val == val 的节点，并返回 新的头节点 。

示例 1：

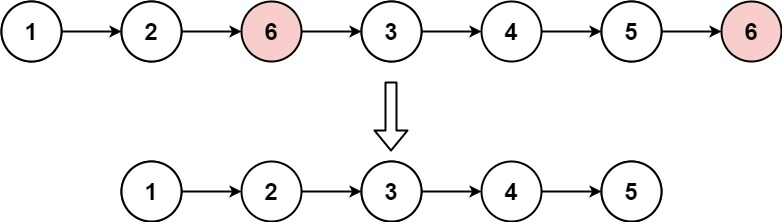
输入：head = [1,2,6,3,4,5,6], val = 6
输出：[1,2,3,4,5]

示例 2：

输入：head = [], val = 1
输出：[]

示例 3：

输入：head = [7,7,7,7], val = 7
输出：[]

解法一：正常遍历

这道题是一道链表的基础题，只需要定义两个变量，一个cur，一个prev，其中cur指向head，prev刚开始指向nullptr，即初始是这样的：

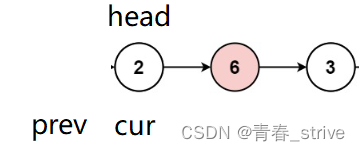
当cur指向的结点不等于val时，prev = cur，cur = cur ->next 即可：

此时cur == val，就让prev -> next = cur -> next，cur = prev -> next 即可：

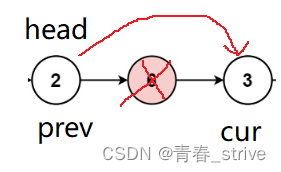
到这里寻常的情况就结束了，还需要考虑特殊的情况，例如第一个结点就是需要删除的结点，此时就不能执行上述逻辑了，因为此时执行prev -> next = cur -> next 这条语句的话，就会造成空指针的问题，所以这里需要特殊处理，刚开始是这样的：

发现需要头删，那就将head = head -> next，cur = head ，这样就不会造成空指针的问题：

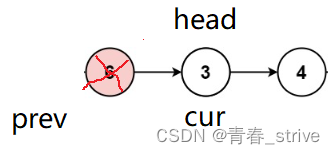
接着进行判断，发现cur指向的结点不等于val，就执行上述正常的操作：

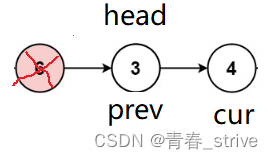
直到循环结束为止

代码如下：

class Solution {
public:
    ListNode* removeElements(ListNode* head, int val) {
        ListNode* cur = head;
        ListNode* prev = nullptr;
        while(cur)
        {
            if(cur->val == val) // 删除
            {
                //头删的情况
                if(cur == head)
                {
                    head = head->next;
                    cur = head;
                }
                //正常的情况
                else
                {
                    prev->next = cur->next;
                    cur = prev->next;
                }
            }
            else //正常向后移动
            {
                prev = cur;
                cur = cur->next;
            }
        }
        return head;
    }
};

解法二：遍历过程中尾插到新链表

在遍历过程中，如果遇到不等于val的结点，就尾插到新链表中，如果等于val就跳过该结点

假设最开始题目所给的条件是这样：

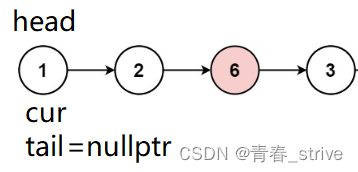
判断cur不等于val，又因为是第一次尾插，所以这一次需要将 cur 赋值给 tail 和 head
再将cur = cur->next 即可：

如果继续cur不等于val，就继续尾插，此时不是第一次尾插就不需要处理 head 了
只需要将 tail -> next = cur，tail = tail -> next，cur = cur -> next就行：

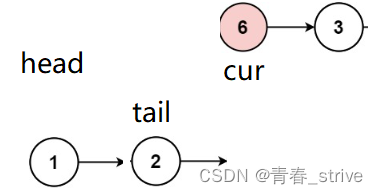
此时cur指向的结点的val等于val，此时该结点不需要尾插，所以直接 cur = cur -> next：

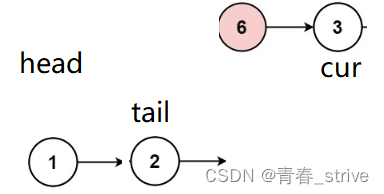
以此类推....

下面会有几个特殊情况可能会出错：

情况一：

当执行结束后，如果原链表的最后一个结点的 val 等于 val 时，这时 cur = cur->next 后，循环就结束了，而此时我新链表的最后一个结点还是指向的原链表的最后一个结点
所以最后需要将tail->next做以处理，将它指向 nullptr 即可

情况二：

而我们如果在代码的最后执行了上述所说的 tail->next = nullptr 操作，有一种特殊情况，如果原链表本身就为空，所以就进不去while循环，此时直接执行这条语句，就会造成空指针的问题，所以还需要针对这种情况做以处理：
在执行 tail->next = nullptr 操作前，先判断head是否等于空

情况三：

如果原链表全部结点的val值都等于val，所以没有一个结点需要尾插到新链表中，此时return的head却是第一个结点，所以此时的head也不为空，却也执行了 tail->next = nullptr 语句，依旧出现空指针错误，所以在刚开始，将cur = head后，将head置为nullptr即可

代码如下：

class Solution {
public:
    ListNode* removeElements(ListNode* head, int val) 
    {
        ListNode* cur = head;
        head = nullptr;//防止所有结点的val都等于val的情况
        ListNode* tail = nullptr;
        while(cur)
        { 
            if(cur->val == val) // 跳过该结点
            {
                cur = cur->next;
            }
            else 
            {
                //尾插
                if(tail == nullptr)//判断是否是第一次尾插
                {
                    head = tail = cur;
                    cur = cur->next;
                }
                else //正常尾插
                {
                    tail->next = cur;
                    tail = tail->next;
                    cur = cur->next;
                }
            }
        }
        //处理原链表最后一个结点的val值为val时，新链表tail->next不为nullptr
        //和原链表本身就是空的情况
        if(head) tail->next = nullptr;
        return head;
    }
};

解法二的新链表变为带有哨兵位的头结点

在最开始，执行完 cur = head 操作后，将tail和head都指向一个new的结点，不需要处理这个结点的值，因为该结点只是哨兵位的头结点，再将 tail->next = nullptr

此时就不需要考虑是否最后可以执行 tail->next = nullptr 操作，因为如果原链表为空，tail是哨兵位的头结点，并不是空指针，所以就可以不需要加 if(head) 这句判断，因此这里可以将上面的情况三也不用考虑了

也不需要处理尾插时是否是第一次尾插的情况，因为已经有哨兵位的头结点赋值给head和tail了，就不需要考虑第一次尾插时将 cur 赋值给 head 和 tail 的问题了

唯一需要注意的一点是，在创建哨兵位的头结点时，因为new了一个结点，所以最后return之前需要delete掉，不然就会内存泄漏，虽然不delete，依旧能过测试用例，但是还是能保持良好的做题习惯最好

代码如下：

class Solution {
public:
    ListNode* removeElements(ListNode* head, int val) 
    {
        ListNode* cur = head;
        ListNode* tail = nullptr;
        tail = head = new ListNode;//创建哨兵位头结点
        tail->next = nullptr; //新链表哨兵位头结点指向nullptr
        while(cur)
        { 
            if(cur->val == val) // 跳过该结点
            {
                cur = cur->next;
            }
            else //尾插
            {
                tail->next = cur;
                tail = tail->next;
                cur = cur->next;
            }
        }
        //处理原链表最后一个结点的val值为val时，新链表tail->next不为nullptr的情况
        tail->next = nullptr;
        //创建哨兵位头结点new的结点需要delete掉
        ListNode* del = head;
        head = head->next;
        delete del;
        return head;
    }
};

题目六：链表分割

给你一个链表的头节点 head 和一个特定值 x ，请你对链表进行分隔，使得所有小于 x 的节点都出现在 大于或等于 x 的节点之前。

需要保留每个分区中各节点的初始相对位置。

示例 1：

输入：head = [1,4,3,2,5,2], x = 3
输出：[1,2,2,4,3,5]

示例 2：

输入：head = [2,1], x = 2
输出：[1,2]

注意题目要求了不能改变原来的数据顺序，所以头插相关的思路就可以舍弃掉了，因为头插会改变顺序，所以想到尾插的思路：

创建两个新链表的头结点，小于x的尾插到 lesshead 后面，大于x的尾插到 greaterhead 后面，最后再将小于x的最后一个结点的next指向greaterhead的第一个结点

需要注意的点是，如果原链表的最后一个结点是小于x的，那么greatertail指向的就是原链表的中间位置的结点，此时greatertail的next不为空，会指向原链表的某一个结点，这时return链表时会出问题，所以在最后需要将greatertail的next置空

代码如下：

class Solution {
public:
    ListNode* partition(ListNode* pHead, int x) {
        ListNode *lesshead, *lesstail, *greaterhead, *greatertail;
        lesshead = lesstail= new ListNode;
        greaterhead = greatertail = new ListNode;
        ListNode* cur = pHead;
        while(cur)
        {
            if(cur->val < x)
            {
                //尾插到lesshead链表中
                lesstail->next = cur;
                lesstail = cur;
                cur = cur->next;
            }
            else
            {
                //尾插到greaterhead链表中
                greatertail->next = cur;
                greatertail = cur;
                cur = cur->next;
            }
        }
        //lesshead链表的尾结点指向greaterhead的头结点
        lesstail->next = greaterhead->next;
        //greatertail的next置空
        greatertail->next = nullptr;
        //delete掉new的结点
        ListNode* delless = lesshead;
        ListNode* delgreater = greaterhead;
        ListNode* head = lesshead->next;
        return head;
    }
};

题目七：链表的回文结构

给定一个链表的 头节点 head ，请判断其是否为回文链表。

如果一个链表是回文，那么链表节点序列从前往后看和从后往前看是相同的。

示例 1：

输入: head = [1,2,3,3,2,1]
输出: true

示例 2：

输入: head = [1,2]
输出: false

这道回文结构的链表题，有时会要求时间复杂度为O(1)，所以创建一个数组，将链表的val放进去，再使用左右双指针进行判断这种思路就pass了，正确的思路应该是：

先使用前面所学的知识找到链表的中间结点，再将中间结点及之后的结点逆置，然后将链表的头结点与中间结点开始一一比较，最终判断出是否是回文结构

如上所示，如果是回文结构，从head和mid开始，一一比较，在mid为空之前，他们的结点的val都是一样的

为了思路更清晰，我们在写此题时，可以将求中间结点和链表的逆置这两个方法写成两个函数，放在同一个类中，在本题所给的函数中调用

代码如下：

class Solution 
{
public:
    //求链表的中间结点
    ListNode* middleNode(ListNode* head)
    {
        //双指针法，一快一慢
        ListNode* slow, *fast;
        slow = fast = head;
        while(fast && fast->next)
        {
            slow = slow->next;
            fast = fast->next->next;
        }
        return slow;
    }
    //链表的逆置，头插所有结点
    ListNode* reverseList(ListNode* head)
    {
        ListNode* cur = head;
        ListNode* newhead = new ListNode;
        newhead->next = nullptr;
        while(cur)
        {
            ListNode* next = cur->next;
            cur->next = newhead->next;
            newhead->next = cur;
            cur = next;
        }
        ListNode* del = newhead;
        ListNode* nowhead = newhead->next;
        delete del;
        return nowhead;
    }

    bool isPalindrome(ListNode* head) 
    {
        ListNode* mid = middleNode(head);//求中间结点
        mid = reverseList(mid); //链表逆置
        ListNode* cur = head;
        while(cur && mid)   //mid与cur，有一个遇空就停止
        {
            if(cur->val != mid->val) return false;
            cur = cur->next;
            mid = mid->next;
        }
        return true;
    }
};

题目八：相交链表

给你两个单链表的头节点 headA 和 headB ，请你找出并返回两个单链表相交的起始节点。如果两个链表不存在相交节点，返回 null 。

图示两个链表在节点 c1 开始相交：

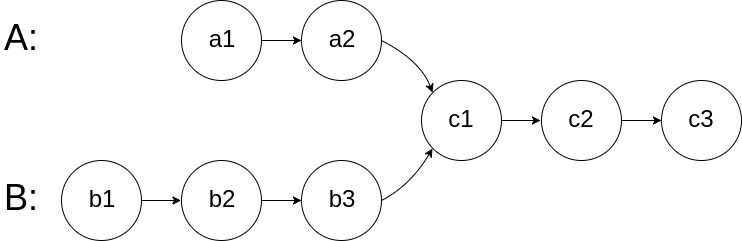
题目数据保证整个链式结构中不存在环。

注意，函数返回结果后，链表必须 保持其原始结构

示例 1：

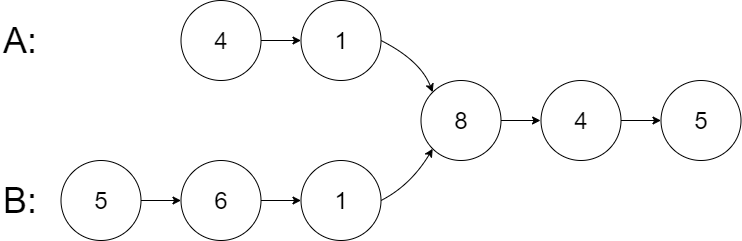
输入：intersectVal = 8, listA = [4,1,8,4,5], listB = [5,6,1,8,4,5], skipA = 2, skipB = 3
输出：Intersected at '8'
解释：相交节点的值为 8 （注意，如果两个链表相交则不能为 0）。
从各自的表头开始算起，链表 A 为 [4,1,8,4,5]，链表 B 为 [5,6,1,8,4,5]。
在 A 中，相交节点前有 2 个节点；在 B 中，相交节点前有 3 个节点。
— 请注意相交节点的值不为 1，因为在链表 A 和链表 B 之中值为 1 的节点 (A 中第二个节点和 B 中第三个节点) 是不同的节点。换句话说，它们在内存中指向两个不同的位置，而链表 A 和链表 B 中值为 8 的节点 (A 中第三个节点，B 中第四个节点) 在内存中指向相同的位置。

示例 2：

输入：intersectVal = 2, listA = [1,9,1,2,4], listB = [3,2,4], skipA = 3, skipB = 1
输出：Intersected at '2'
解释：相交节点的值为 2 （注意，如果两个链表相交则不能为 0）。
从各自的表头开始算起，链表 A 为 [1,9,1,2,4]，链表 B 为 [3,2,4]。
在 A 中，相交节点前有 3 个节点；在 B 中，相交节点前有 1 个节点。

示例 3：

输入：intersectVal = 0, listA = [2,6,4], listB = [1,5], skipA = 3, skipB = 2
输出：null
解释：从各自的表头开始算起，链表 A 为 [2,6,4]，链表 B 为 [1,5]。
由于这两个链表不相交，所以 intersectVal 必须为 0，而 skipA 和 skipB 可以是任意值。
这两个链表不相交，因此返回 null 。

首先最先想到的暴力解法就是，listA的所有结点都与listB的所有结点比较一遍，看地址是否相同，这种实现方式比较简单，且时间复杂度为O(N^2)，这里就不列举了

下面说一种时间复杂度为O(N)的思路就能解决：

分别求两个链表的长度，让长的先走差距步数，此时再同时走，每次观察地址是否相同就能够解决问题，因为此时两个链表的长度相同，在分别向后遍历时，若相交则必定会出现相同地址

此处可以优化的一点是，如果两个链表相交，那么他们的最后一个结点必定相同，所以我们在求长度时，可以求出两个链表的尾结点，求出来后可以进行比较，如果尾结点不同，那就不用做下面的操作了，因为尾结点不同的话两个链表必定不会相交

代码如下：

class Solution {
public:
    ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) 
    {
        ListNode *curA = headA;
        ListNode *curB = headB;
        int numA = 0, numB = 0;
        while(curA->next)//求A的尾结点并求A的长度
        {
            curA = curA->next;
            numA++;
        }
        while(curB->next)//求B的尾结点并求B的长度
        {
            curB = curB->next;
            numB++;
        }
        if(curA != curB) return nullptr;
        //先随机指定长链表和短链表
        ListNode* shortList = headA, *longList = headB;
        if(numA > numB)//如果进入if语句，说明指定错误，进行修正
        {
            shortList = headB;
            longList = headA;
        }
        int gap = abs(numA - numB);
        while(gap--) longList = longList->next;//长的走差距步
        while(shortList != longList)
        {
            shortList = shortList->next;
            longList = longList->next;
        }
        //走到这里，说明一定相遇了，返回相遇结点
        return shortList;
    }
};

题目九：环形链表I

给你一个链表的头节点 head ，判断链表中是否有环。

如果链表中有某个节点，可以通过连续跟踪 next 指针再次到达，则链表中存在环。为了表示给定链表中的环，评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。注意：pos 不作为参数进行传递 。仅仅是为了标识链表的实际情况。

如果链表中存在环 ，则返回 true 。否则，返回 false 。

示例 1：

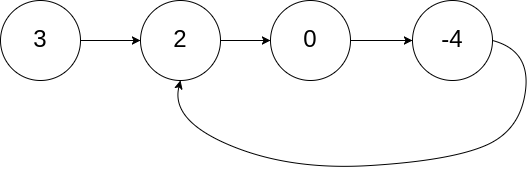
输入：head = [3,2,0,-4], pos = 1
输出：true
解释：链表中有一个环，其尾部连接到第二个节点。

示例 2：

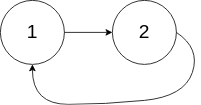
输入：head = [1,2], pos = 0
输出：true
解释：链表中有一个环，其尾部连接到第一个节点。

示例 3：

输入：head = [1], pos = -1
输出：false
解释：链表中没有环。

关于环形链表，也就是尾结点的next不指向空，继续指向链表中的结点，从而遍历时造成循环的效果，这就称之为环形链表，而普通链表就是尾结点的next指向空的链表

解法一：遍历每个结点都与之前的所有结点比较

最容易想到的思路就是：遍历到每个结点时，都记录下该结点，下次判断是否出现重复的结点，这种方式的空间复杂度比较高，效率比较低，这里就不实现了

解法二：使用map每次记录结点，判断是否出现过

使用map的思路，结合上述的想法，每次遍历到新结点时判断是否出现，map就不会像上面的那种方式，每次都需要从头到尾比较一遍，map比较的效率是非常高的

class Solution {
public:
    bool hasCycle(ListNode *head) 
    {
        unordered_map<ListNode*, int> mp;
        ListNode* cur = head;
        while(cur)
        {
            if(!mp.count(cur)) mp[cur]++;
            else return true;
            cur = cur->next;
        }
        return false;
    }
};

解法三：快慢指针

下面是第三种思路，借助前面用过的方法：快慢指针

定义两个指针，fast、slow表示快慢指针，快指针一次走两步，慢指针一次走一步，如果链表有环，那么快慢指针是一定会在环中相遇的，如果没环，快指针会走到空

代码如下：

class Solution {
public:
    bool hasCycle(ListNode *head) 
    {
        ListNode *fast = head, *slow = head;
        while(fast && fast->next)
        {
            fast = fast->next->next;
            slow = slow->next;
            if(fast == slow) return true;
        }
        return false;
    }
};

到这里已经解决了这道问题，那么怎么证明在环中fast一定会追到slow呢，其实很简单，fast每次走两步，而slow每次走一步，每走一步两者的距离会缩小一步，那么肯定一步一步就追上了

但是如果fast一次走3步.....n步，slow每次走1步，那么这时就不一定会追上了，如果fast是3步，所以此时每走一步距离缩短两步，如果两者相隔的距离是偶数可以追上，如果相隔的距离是奇数，那每次都快2步，最后始终会隔1步，就会有一种可能始终遇不到

题目十：环形链表II

给定一个链表的头节点 head ，返回链表开始入环的第一个节点。 如果链表无环，则返回 null。

如果链表中有某个节点，可以通过连续跟踪 next 指针再次到达，则链表中存在环。为了表示给定链表中的环，评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。如果 pos 是 -1，则在该链表中没有环。注意：pos 不作为参数进行传递，仅仅是为了标识链表的实际情况。

不允许修改 链表。

示例 1：

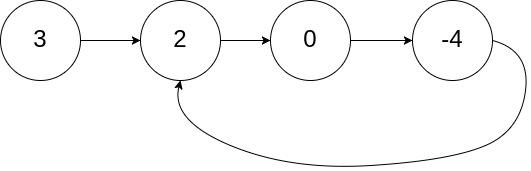
输入：head = [3,2,0,-4], pos = 1
输出：返回索引为 1 的链表节点
解释：链表中有一个环，其尾部连接到第二个节点。

示例 2：

输入：head = [1,2], pos = 0
输出：返回索引为 0 的链表节点
解释：链表中有一个环，其尾部连接到第一个节点。

示例 3：

输入：head = [1], pos = -1
输出：返回 null
解释：链表中没有环。

这道题和上一道题一样，只不过这道题求的是如果相遇，return相遇的结点

解法一：数学思维

假设一个链表从head开始到相遇结点的长度为L，这个链表的环长度为C，快指针进入环已经走了N圈，最终与慢指针在meet位置相遇，相遇结点到meet的长度为x，如下图所示：

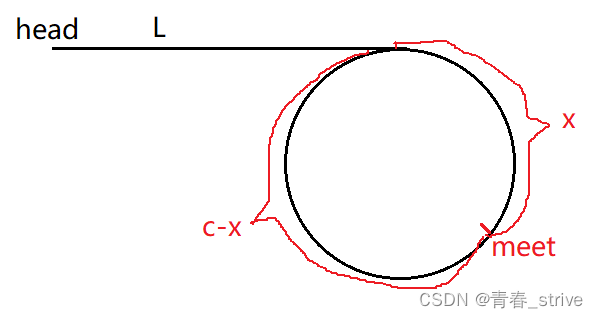
slow指针总共走了：L + X长度
fast指针总共走了：L + N*C + X长度

那么既然快指针是满指针的两倍速度，所以走的路程也就是两倍了，就得到下面这个公式：

2*(L + X) = L + N*C + X
L + X = N*C
L = N*C - X
L = (N-1)*C + (C - X)

上面得到的公式表示，L的长度，与从环中meet位置开始走N-1圈后，再走C-X长度相同

所以对照上面的图，得到一个结论：
一个指针从head位置走，另一个指针从meet位置走，会在环的第一个结点相遇

所以这里的思路就是先使用上一题的方法，找到上一题 return true 的位置，也就是就是meet的位置，再进行实现

将上述的思路转换为代码，如下所示：

class Solution {
public:
    ListNode *detectCycle(ListNode *head) 
    {
        ListNode *fast = head, *slow = head;
        while(fast && fast->next)
        {
            slow = slow->next;
            fast = fast->next->next;
            //找到meet结点
            if(fast == slow)
            {
                //开始两个指针，分别从head和meet位置走
                ListNode *meet = fast;
                while(meet != head)
                {
                    meet = meet->next;
                    head = head->next;
                }
                //走到这说明已经走了C-X距离后相遇了
                return meet;
            }
        }
        return nullptr;
    }
};

解法二：将环形链表转换为链表相交问题

就按上面的这个图来说：

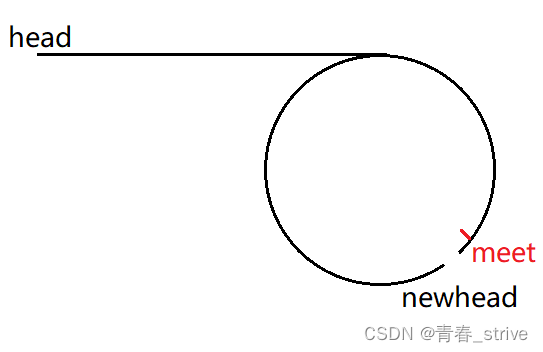
我们将meet结点指向空，再将meet结点的下一个结点定为newhead，此时将newhead展开：

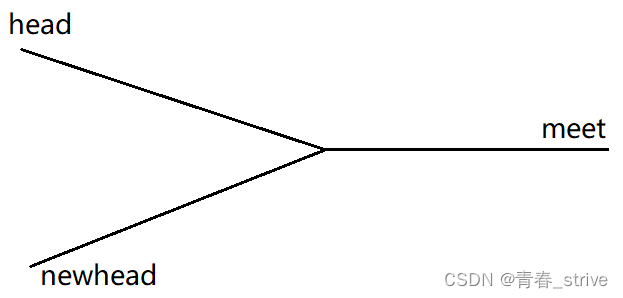
此题就转变为了链表相交问题，继续使用前面的快慢指针做即可

可以在转化后，调用之前写过的相交链表的函数即可：

class Solution {
public:
    //相交链表的解题代码
    ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) 
    {
        ListNode *curA = headA;
        ListNode *curB = headB;
        int numA = 0, numB = 0;
        while(curA->next)//求A的尾结点并求A的长度
        {
            curA = curA->next;
            numA++;
        }
        while(curB->next)//求B的尾结点并求B的长度
        {
            curB = curB->next;
            numB++;
        }
        if(curA != curB) return nullptr;
        //先随机指定长链表和短链表
        ListNode* shortList = headA, *longList = headB;
        if(numA > numB)//如果进入if语句，说明指定错误，进行修正
        {
            shortList = headB;
            longList = headA;
        }
        int gap = abs(numA - numB);
        while(gap--) longList = longList->next;//长的走差距步
        while(shortList != longList)
        {
            shortList = shortList->next;
            longList = longList->next;
        }
        //走到这里，说明一定相遇了，返回相遇结点
        return shortList;
    }
    ListNode *detectCycle(ListNode *head) 
    {
        ListNode *fast = head, *slow = head;
        while(fast && fast->next)
        {
            slow = slow->next;
            fast = fast->next->next;
            //找到meet结点
            if(fast == slow)
            {
                ListNode *newhead = fast->next;
                fast->next = nullptr;
                //调用之前写的链表相交的函数
                return getIntersectionNode(head,newhead);
            }
        }
        return nullptr;
    }
};

题目十一：随机链表的复制

给你一个长度为 n 的链表，每个节点包含一个额外增加的随机指针 random ，该指针可以指向链表中的任何节点或空节点。

构造这个链表的 深拷贝。深拷贝应该正好由 n 个全新节点组成，其中每个新节点的值都设为其对应的原节点的值。新节点的 next 指针和 random 指针也都应指向复制链表中的新节点，并使原链表和复制链表中的这些指针能够表示相同的链表状态。复制链表中的指针都不应指向原链表中的节点 。

例如，如果原链表中有 X 和 Y 两个节点，其中 X.random --> Y 。那么在复制链表中对应的两个节点 x 和 y ，同样有 x.random --> y 。

返回复制链表的头节点。

用一个由 n 个节点组成的链表来表示输入/输出中的链表。每个节点用一个 [val, random_index] 表示：

val：一个表示 Node.val 的整数。
random_index：随机指针指向的节点索引（范围从 0 到 n-1）；如果不指向任何节点，则为 null 。

你的代码只接受原链表的头节点 head 作为传入参数。

示例 1：

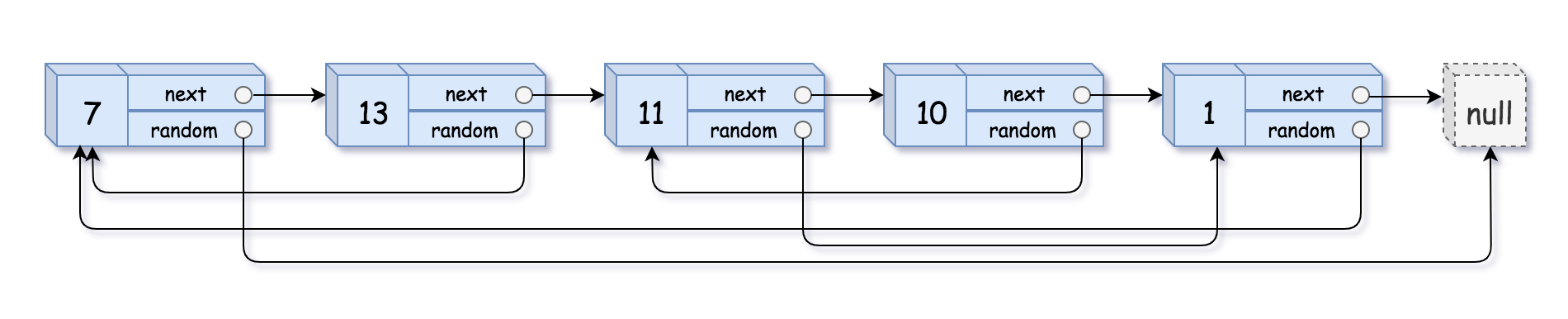
输入：head = [[7,null],[13,0],[11,4],[10,2],[1,0]]
输出：[[7,null],[13,0],[11,4],[10,2],[1,0]]

示例 2：

输入：head = [[1,1],[2,1]]
输出：[[1,1],[2,1]]

示例 3：

输入：head = [[3,null],[3,0],[3,null]]
输出：[[3,null],[3,0],[3,null]]

这道题的题意就是：构造一个新链表，使得这个新链表和原链表中每一个结点的两个指针都指向的一样，类似于进行一个深拷贝

解法一：不借助容器

而这里所给的链表，每个结点都有两个指针，其中一个就是普通的next指针，还有一个是random指针，表示随机指向链表中的某个位置，这道题的难点就是这个random指针，怎么深拷贝出来

因为next指针可以遍历时一步一步拷贝，而random指针所指向的结点，原链表和新深拷贝出来的链表地址是不同的，所以就需要仔细思考如何处理这个问题

可能有一种想法是原链表指向的结点的val时多少，我就在新链表中找这个 val值的结点，但是这种思路可能会出现多个 val值相同的结点，会有问题，就算链表的 val值不重复，效率也是非常低的，每个结点都需要遍历一遍链表，时间复杂度为O(N^2)了

所以下面讲讲正确的思路：

第一步、将copy的每个结点都链接到源结点的后面
变为：

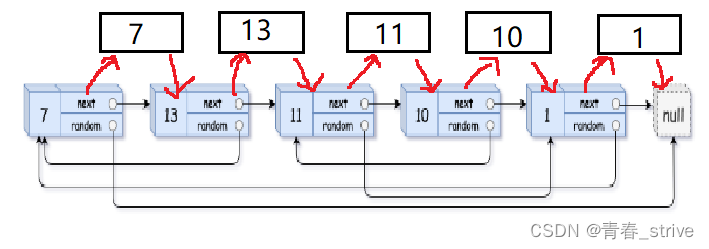
第二步、开始遍历原链表，copy->random = cur->random->next

如果原链表cur->random指向nullptr，那copy->random也指向nullptr

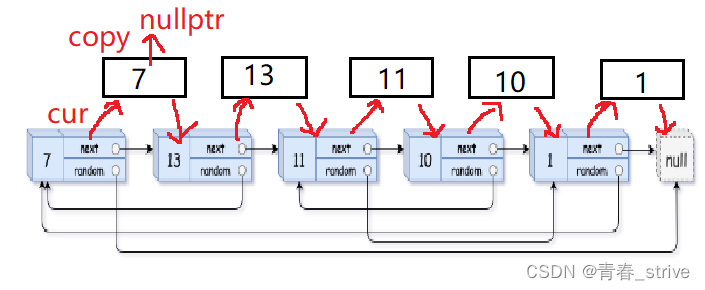
如果原链表cur->random不指向空，那么执行copy->random = cur->random->next

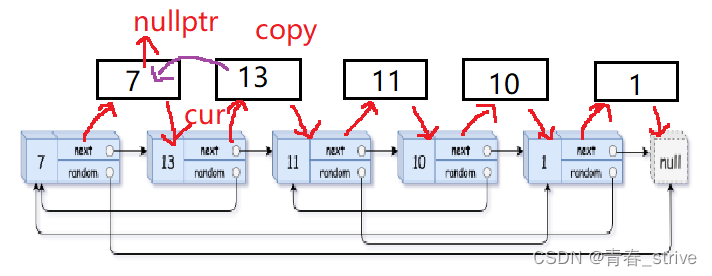
因为原链表cur结点的random指向的是第一个结点，所以copy->random就指向原结点的random的下一个结点，也就是深拷贝出的这个结点，就能够完美的找到拷贝结点的random指向的结点，只要能够找到原结点的random指向，那么copy结点的random指向就是原结点的next结点

能够进行上述操作的前提就是，我们第一步做的将copy结点链接到了原结点的后面，这样就能够找到copy结点的random指向的结点了

第三步、拷贝节点解下来，链接到一起，恢复原链表

从而得到了随机链表的复制，代码如下：

class Solution 
{
public:
    Node* copyRandomList(Node* head) 
    {
        // 1.拷贝链表到原链表的后面
        Node* cur = head;
        while(cur)
        {
            Node* next = cur->next;
            Node* copy = new Node(cur->val);
            cur->next = copy;//改变cur->next指向
            copy->next = next;//改变copy->next指向
            cur = next;
        }
        // 2.遍历链表，实现copy结点的random指针的指向
        cur = head;
        while(cur)
        {
            Node* copy = cur->next;
            if(cur->random)//cur->random不指向空
                copy->random = cur->random->next;
            else //cur->random指向空
                copy->random = nullptr;
            cur = copy->next;
        }
        // 3.将拷贝结点解下来
        cur = head;
        Node* newhead = new Node(0);
        newhead->next = nullptr;
        Node* tail = newhead;
        while(cur)
        {
            Node* copy = cur->next;
            cur->next = copy->next;
            cur = cur->next;//cur继续往后走
            tail->next = copy;
            tail = copy;
        }
        return newhead->next;
    }
};

解法二：使用哈希表进行映射

使用map，将源节点与拷贝节点进行映射，也是能够实现的

代码如下：

class Solution 
{
public:
    Node* copyRandomList(Node* head) 
    {
        if(head == nullptr) return nullptr;
        unordered_map<Node*, Node*> mp;
        Node* cur = head;
        while(cur)
        {
            Node* copy = new Node(cur->val);
            mp[cur] = copy;//原链表与拷贝链表结点一一对应
            cur = cur->next;
        }
        cur = head;
        while(cur)
        {
            //依靠哈希表进行random和next的指向
            mp[cur]->random = mp[cur->random];
            mp[cur]->next = mp[cur->next];
            cur = cur->next;
        }
        return mp[head];
    }
};

题目十二：两数相加

给你两个非空的链表，表示两个非负的整数。它们每位数字都是按照逆序的方式存储的，并且每个节点只能存储一位数字。

请你将两个数相加，并以相同形式返回一个表示和的链表。

你可以假设除了数字 0 之外，这两个数都不会以 0 开头。

示例 1：

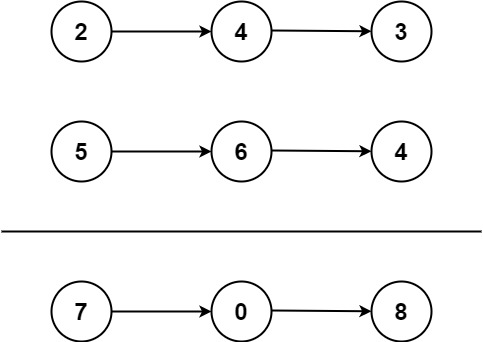
输入：l1 = [2,4,3], l2 = [5,6,4]
输出：[7,0,8]
解释：342 + 465 = 807.

示例 2：

输入：l1 = [0], l2 = [0]
输出：[0]

示例 3：

输入：l1 = [9,9,9,9,9,9,9], l2 = [9,9,9,9]
输出：[8,9,9,9,0,0,0,1]

提示：

每个链表中的节点数在范围 [1, 100] 内
0 <= Node.val <= 9
题目数据保证列表表示的数字不含前导零

首先题目明确说明了，链表所表示的数字是按照逆序的方式存储的，也就是原本是128，那么链表中存储的就是821，这样是为了方便我们计算的，因为我们在做加法时，就是从后往前开始加的，这里链表逆序的话，我们直接从头往后加即可

在这道题的while判断条件中，条件不是 &&，而是 ||，因为加法运算，一个数没有了就不计算这个了，把它当做0即可

while的条件中还有 || num，因为可能两个数的最后一位加完，还有进位num，所以这时还需要再new一个结点出来，存储这个进位

代码如下：

class Solution {
public:
    ListNode* addTwoNumbers(ListNode* l1, ListNode* l2) 
    {
        ListNode* cur1 = l1, *cur2 = l2;
        ListNode* newhead = new ListNode(0);//哨兵位头结点
        newhead->next = nullptr;
        ListNode* tail = newhead;//尾指针
        int num = 0; //记录进位
        while(cur1 || cur2 || num)
        {
            if(cur1) //cur1不为空
            {
                num += cur1->val;
                cur1 = cur1->next;
            }
            if(cur2) //cur2不为空
            {
                num += cur2->val;
                cur2 = cur2->next;
            }
            ListNode* node = new ListNode(num % 10);//将个位给node
            num /= 10; //num表示进位，所以除10，保留十位
            tail->next = node;
            tail = node;
        }
        ListNode* del = newhead;//释放new出的哨兵位头结点
        ListNode* head = newhead->next;
        delete newhead;
        return head;
    }
};

题目十三：两两交换链表中的结点

给你一个链表，两两交换其中相邻的节点，并返回交换后链表的头节点。你必须在不修改节点内部的值的情况下完成本题（即，只能进行节点交换）。

示例 1：

输入：head = [1,2,3,4]
输出：[2,1,4,3]

示例 2：

输入：head = []
输出：[]

示例 3：

输入：head = [1]
输出：[1]

这道题后面在递归的题目练习中也会使用做到，这里使用的是循环、迭代的方式

先new一个哨兵位头结点，就不需要额外的处理一些边界条件了

为了方便交换，可以多定义几个变量，cur的前一个结点为prev，遍历的当前结点为cur，与当前结点进行交换的为next，next的下一个结点为nnext，如下所示：

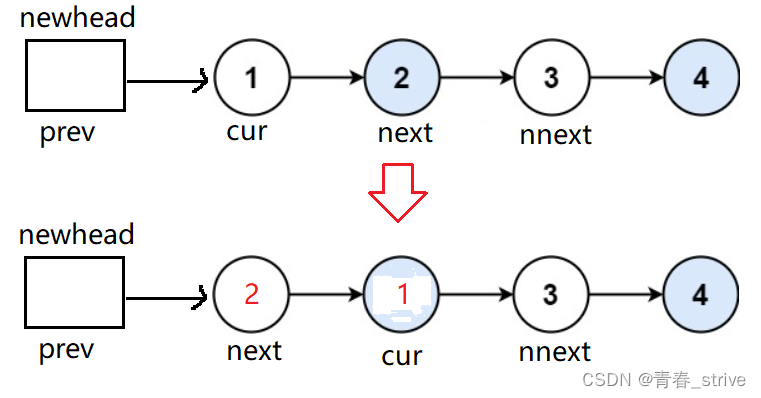
上图是交换完以后的指针对应情况，接下来应该变为prev、cur、next、nnext这个顺序：

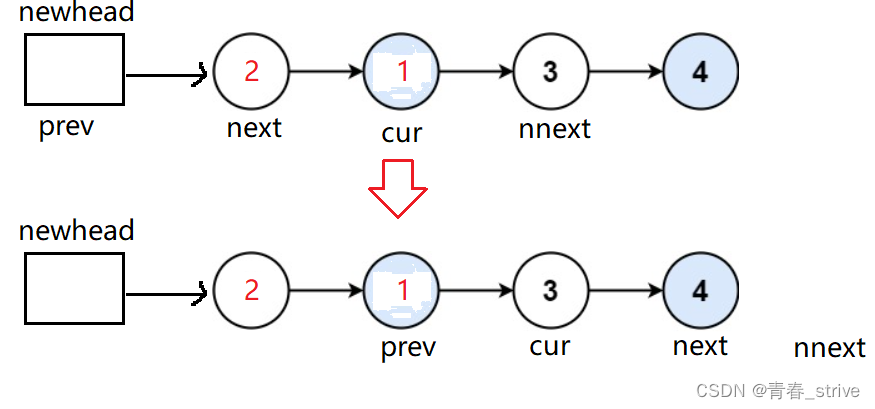
所以就需要循环一次以后改变上述指针的对应位置

下面说明循环的结束条件，如果是偶数的情况，cur走到这一步就该停止循环了：

如果是奇数的情况，cur走到这一步就该停止循环了：

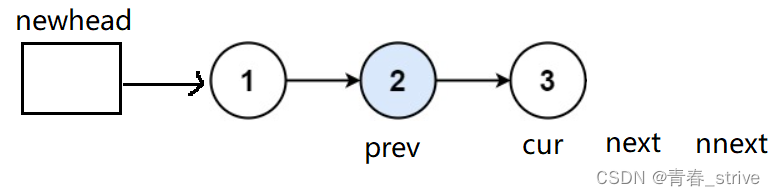
所以结束条件就是，cur&&next为空就停止

代码如下：

class Solution 
{
public:
    ListNode* swapPairs(ListNode* head) 
    {
        if(head == nullptr || head->next == nullptr) return head;
        ListNode* newhead = new ListNode;
        newhead->next = head;
        //定义四个指针，分别指向包含哨兵位的前四个结点
        ListNode* prev = newhead, *cur = prev->next, *next = cur->next, *nnext = next->next;
        while(cur && cur->next)
        {
            //交换后的各个指针的指向情况
            prev->next = next;
            next->next = cur;
            cur->next = nnext;
            //改变prev、cur、next和nnext的指向
            prev = cur;
            cur = nnext;
            //如果cur或是next为空，就表示是链表个数是奇数个，下一次就停止循环了
            //此时就不能给next和nnext赋值了，不然就会出现空指针问题
            if(cur) next = cur->next;
            if(next) nnext = next->next;
        }
        return newhead->next;
    }
};

题目十四：重排链表

给定一个单链表 L 的头节点 head ，单链表 L 表示为：

L0 → L1 → … → Ln - 1 → Ln

请将其重新排列后变为：

L0 → Ln → L1 → Ln - 1 → L2 → Ln - 2 → …

不能只是单纯的改变节点内部的值，而是需要实际的进行节点交换。

示例 1：

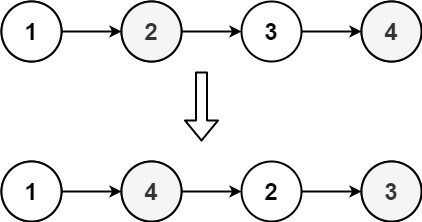
输入：head = [1,2,3,4]
输出：[1,4,2,3]

示例 2：

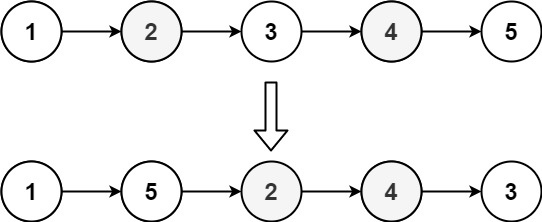
输入：head = [1,2,3,4,5]
输出：[1,5,2,4,3]

这道题要求将一个给定的链表，第一个结点->最后一个结点->第二个结点->倒数第二个结点 ...

按照这种顺序排列，例如1->2->3->4变为1->4->2->3

仔细观察变化后的链表，我们可以发现，如果将原链表从中间位置切成两部分，将后半部分逆置，也就是变为了1->2->4->3，此时前半部分是1->2，后半部分是4->3，接着前半部分取一个数，后半部分取一个数，这样依次取值，就得到了1->4->2->3的结果

所以这道题分为三步：

①找到链表的中间结点
②后半部分链表逆序
③合并两个链表

可以看到这三步，在前面都是做过类似的题目的，下面分析一下题目的细节

第一步找链表的中间结点，是用快慢双指针的方法找到的中间结点，此时slow指向的就是中间结点

第二步后半部分链表逆序，有两种方式，第一种是从slow开始逆序，第二种是从slow->next开始逆序

第一种方式很好理解，因为从哪里划分的就从哪里逆序，那么为什么要有第二种呢，很简单，因为第三步是合并两个链表，需要有两个单独的链表，前半部分的最后一个结点时需要指向空的

如果是第二种方式，我想断开前半部分和后半部分，只需要将slow->next = nullptr即可，因为slow可以归属到前半部分去，不需要做其他处理，而第一种找到中间结点后无法找到前半部分的最后一个结点，将前半部分置空，下面说说为什么可以这样做：

如果是奇数个结点，这样做很好理解，那如果是偶数个，例如原链表为1->2->3->4，找到的中间结点是3，那么这种方式就是从结点4开始逆序，重排以后应该是1->4->2->3，观察最终结果，中间结点和它前面的结点也就是2和3，在重排完之后依旧是连在一起的，所以在这种方式下我们可以将中间结点归到前半部分去，最终的结果也是正确的

第三步合并两个链表，经过上面的步骤，成功将两个链表断开了，下面只需要将这两个断开的链表尾插到新链表中即可，循环的判断条件为第一个链表不为空，因为无论是奇数还是偶数都是第一个链表的结点数量多，如下所示：

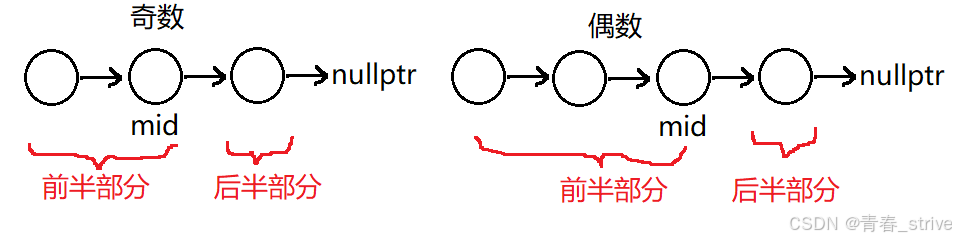
代码如下：

class Solution {
public:
    void reorderList(ListNode* head) {
        //如果没有结点，或是只有1个或2个结点，直接return，因为顺序不变
        if(head == nullptr || head->next == nullptr || head->next->next == nullptr) return;
        //找中间结点，快慢双指针
        ListNode* fast = head, *slow = head;
        while(fast && fast->next)
        {
            slow = slow->next;
            fast = fast->next->next;
        }
        //逆序后半部分链表
        ListNode* newhead = new ListNode;//创建哨兵位头结点
        ListNode* cur = slow->next; //从slow->next开始逆序
        slow->next = nullptr; //将前半部分最后一个结点指向空，断开两个链表
        while(cur) 
        {
            ListNode* next = cur->next;
            cur->next = newhead->next;
            newhead->next = cur;
            cur = next;
        }
        //合并两个链表
        ListNode* ret = new ListNode;
        ListNode* tail = ret;
        ListNode* cur1 = head, *cur2 = newhead->next;
        while(cur1)
        {
            //先尾插第一个链表
            tail->next = cur1;
            cur1 = cur1->next;
            tail = tail->next;
            //再尾插第二个链表，可能为空，所以需要先判断
            if(cur2)
            {
                tail->next = cur2;
                cur2 = cur2->next;
                tail = tail->next;
            }
        }
        //释放new的结点
        delete newhead;
        delete ret;
    }
};

题目十五：合并 k 个升序链表

给你一个链表数组，每个链表都已经按升序排列。

请你将所有链表合并到一个升序链表中，返回合并后的链表。

示例 1：

输入：lists = [[1,4,5],[1,3,4],[2,6]]
输出：[1,1,2,3,4,4,5,6]
解释：链表数组如下：
[
  1->4->5,
  1->3->4,
  2->6
]
将它们合并到一个有序链表中得到。
1->1->2->3->4->4->5->6

示例 2：

输入：lists = []
输出：[]

示例 3：

输入：lists = [[]]
输出：[]

解法一：暴力解法

暴力解法就是：先合并前两个有序链表为一个新链表，再接着两两往下合并，由于这种算法的时间复杂度过大，所以代码就不写了，看下面的解法

解法二：优先级队列做优化

这种解法参考了上面做过的合并两个有序链表的题目，由于在合并两个有序链表那里，只有两个链表，所以比较好比较哪个链表的当前结点是较小的那一个，而这道题是k个链表，采用比较的方式不太好比较谁是较小的结点，所以引入了优先级队列(小根堆)，将k个链表的当前指向的结点都放入优先级队列中，堆顶结点就是最小的结点，此时拿出堆顶的结点尾插入新链表中，再将该结点所在的链接向后移动，继续插入优先级队列中

这种算法的时间复杂度是O(N* K * logK)，每个链表长度为N，有K个链表，优先级队列的时间复杂度为logK

代码如下：

class Solution {
public:
    //cmp仿函数，判断每个结点的val值
    struct cmp
    {
        bool operator()(const ListNode* t1, const ListNode* t2)
        {
            return t1->val > t2->val;//大于就向下调整
        }
    };

    ListNode* mergeKLists(vector<ListNode*>& lists) 
    {
        //创建一个小根堆
        priority_queue<ListNode*, vector<ListNode*>, cmp> heap;
        //让所有链表的头结点进入小根堆
        for(auto& iter : lists)
        {
            if(iter) heap.push(iter);
        }
        //创建哨兵位头结点，合并k个链表
        ListNode* newhead = new ListNode;
        ListNode* tail = newhead;
        while(!heap.empty())
        {
            ListNode* small = heap.top();
            heap.pop();
            tail->next = small;
            tail = small;
            small = small->next;
            //判断当前结点是否为空
            if(small) heap.push(small);
        }
        //释放new出来的头结点
        ListNode* del = newhead;
        ListNode* head = newhead->next;
        delete del;
        return head;
    }
};

解法三：分治 - 递归

这道题如果使用递归分治的思路，时间复杂度依旧是O(N*K*logK)，分析如下：

假设有K个链表，那么二叉树的高度就是logK，链表中有N个结点，每个结点都会合并logK次，此时每个链表的时间复杂度是O(N*logK)，又因为有K个链表，所以时间复杂度是O(N*K*logK)

这道题的递归解法，与前面的分治中递归的解法，几乎一模一样，只不过之前是每次合并两个数组，这道题是每次合并两个链表

代码如下：

class Solution {
public:

    ListNode* mergeKLists(vector<ListNode*>& lists) 
    {
        if(lists.size() == 0) return nullptr;
        if(lists.size() == 1) return lists[0];
        return merge(lists, 0, lists.size()-1);
    }

    ListNode* merge(vector<ListNode*>& lists, int left, int right)
    {
        if(left > right) return nullptr;;
        if(left == right) return lists[left];;

        //左右区间排序
        int mid = ((right - left) >> 1) + left;
        ListNode* cur1 = merge(lists, left, mid);
        ListNode* cur2 = merge(lists, mid + 1, right);

        //合并两个链表
        ListNode* newhead = new ListNode;
        ListNode* tail = newhead;
        while(cur1 && cur2)
        {
            if(cur1->val < cur2->val)
            {
                tail->next = cur1;
                tail = cur1;
                cur1 = cur1->next;
            }
            else
            {
                tail->next = cur2;
                tail = cur2;
                cur2 = cur2->next;
            }
        }
        //处理两个链表可能有一个还有元素的情况
        if(cur1) tail->next = cur1;
        if(cur2) tail->next = cur2;
        //new的结点delete掉
        ListNode* del = newhead;
        ListNode* head = newhead->next;
        delete del;
        return head;
    }
};

题目十六：K 个一组翻转链表

给你链表的头节点 head ，每 k 个节点一组进行翻转，请你返回修改后的链表。

k 是一个正整数，它的值小于或等于链表的长度。如果节点总数不是 k 的整数倍，那么请将最后剩余的节点保持原有顺序。

你不能只是单纯的改变节点内部的值，而是需要实际进行节点交换。

示例 1：

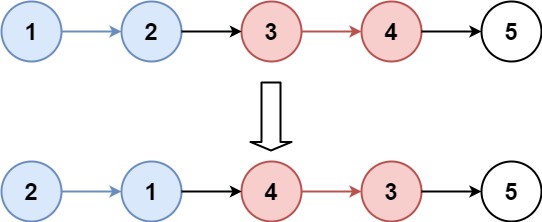
输入：head = [1,2,3,4,5], k = 2
输出：[2,1,4,3,5]

示例 2：

输入：head = [1,2,3,4,5], k = 3
输出：[3,2,1,4,5]

这道题其实就是模拟，模拟给你的算法过程

首先我们需要知道这个链表需要逆序多少组，在知道需要逆序n组后，只需要重复n次逆序过程，并且保证每次逆序完成后，能够保持链表的链接关系即可

以示例一举例：head = [1,2,3,4,5]，k = 2

链表中共5个结点，k = 2，所以5 / 2 = 2，算出来需要逆序2组，也就是 [1,2] 和 [3,4]，最后的这个[5]不用动，链接到前两组逆序完以后得后面即可

逆序完 [1,2]，变为 [2,1]，此时逆序 [3,4] 的时候，需要跟在结点1后面，所以为了方便起见，提前记录结点1，这样下次逆序时就能很快找到该结点

逆序的过程已经做过非常多的题目了，也就是头插法

代码如下：

class Solution {
public:
    ListNode* reverseKGroup(ListNode* head, int k) 
    {
        ListNode* cur = head;
        int num = 0;
        //计算链表中结点的个数
        while(cur)
        {
            num++;
            cur = cur->next;
        }
        //num就是需要逆序的数组个数
        num /= k;
        //创建哨兵位头结点，方便头插
        ListNode* newhead = new ListNode;
        ListNode* prev = newhead;
        prev->next = nullptr;
        cur = head;      
        while(num--)
        {
            int ret = k;
            ListNode* tmp = cur;//记录下一次需要头插的位置
            while(ret--)
            {
                ListNode* next = cur->next;
                cur->next = prev->next;
                prev->next = cur;
                cur = next;
            }
            prev = tmp;//更新prev，也就是下一次需要头插的位置
            prev->next = nullptr;
        }
        //把不需要反转的结点接上
        prev->next = cur;
        ListNode* del = newhead;
        ListNode* ret = newhead->next;
        delete del;
        return ret;
    }
};

链表题目到此结束啦