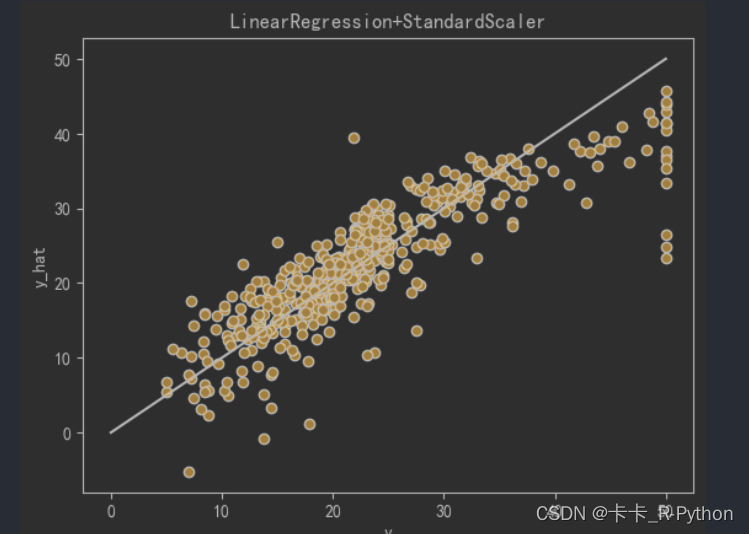
1.采用散点图绘制相关性。
#分析波士顿房价数据集的数据相关性
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
#载入数据集
data_url = "http://lib.stat.cmu.edu/datasets/boston"
raw_df = pd.read_csv(data_url, sep="\s+", skiprows=22, header=None)
boston = np.hstack([raw_df.values[::2, :], raw_df.values[1::2, :2]])
target = raw_df.values[1::2, 2]
x = boston
y = target
plt.scatter(x[:, 5], y)
plt.show()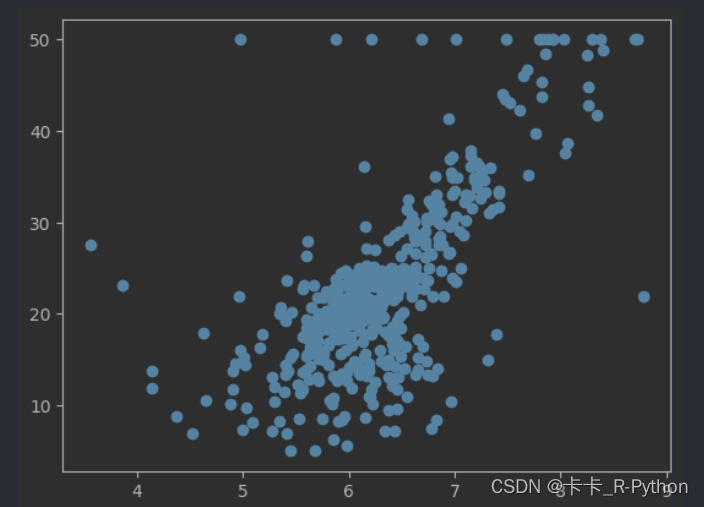
2.输出出数据结构
print (u'形状:', x.shape)
print (x[:10]) 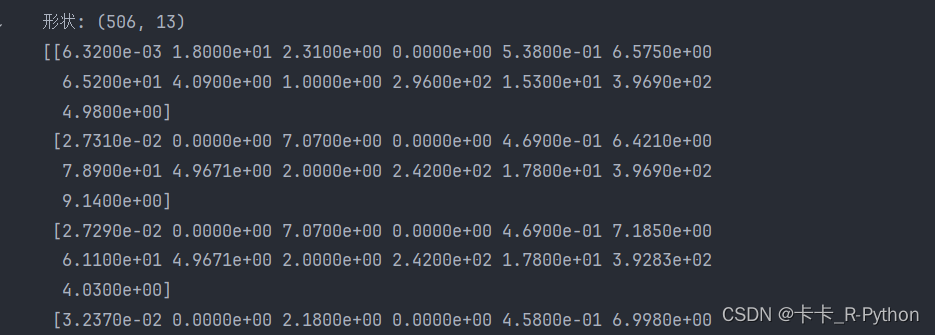
3.PCA
#PCA降维
from sklearn.decomposition import PCA
pca = PCA(n_components=2)
newData = pca.fit_transform(x)
print (u'降维后数据:')
print (newData[:4])
print (u'形状:', newData.shape) 
4.Lasso回归分析
import matplotlib.pyplot as plt
plt.rcParams["font.sans-serif"]=["SimHei"] #设置字体
plt.rcParams["axes.unicode_minus"]=False #该语句解决图像中的“-”负号的乱码问题
# 从sklearn.cross_validation 导入数据分割器。
from sklearn.model_selection import train_test_split
# 导入 numpy 并重命名为 np。
import numpy as np
from sklearn.linear_model import Ridge,Lasso
X = boston
y = target
# 随机采样 25% 的数据构建测试样本,其余作为训练样本。
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=33, test_size=0.25)
# 分析回归目标值的差异。
print("The max target value is", np.max(target))
print("The min target value is", np.min(target))
print("The average target value is", np.mean(target))
# 从 sklearn.preprocessing 导入数据标准化模块。
from sklearn.preprocessing import StandardScaler
from sklearn.preprocessing import MinMaxScaler
from sklearn.preprocessing import Normalizer
# 分别初始化对特征和目标值的标准化器。
ss_X = StandardScaler()
ss_y = StandardScaler()
ss="StandardScaler"
# 分别对训练和测试数据的特征以及目标值进行标准化处理。
X_train = ss_X.fit_transform(X_train)
X_test = ss_X.transform(X_test)
y_train = ss_y.fit_transform(y_train.reshape(-1, 1))
y_test = ss_y.transform(y_test.reshape(-1, 1))
# 从 sklearn.linear_model 导入 LinearRegression。
from sklearn.linear_model import LinearRegression
# 使用默认配置初始化线性回归器 LinearRegression。
def train_model():
lr = LinearRegression()
# 使用训练数据进行参数估计。
lr.fit(X_train, y_train[:,0])
# 对测试数据进行回归预测。
lr_y_predict = lr.predict(X_test)
# 从 sklearn.linear_model 导入 SGDRegressor。
from sklearn.linear_model import SGDRegressor
# 使用默认配置初始化线性回归器 SGDRegressor。
sgdr = SGDRegressor()
# 使用训练数据进行参数估计。
sgdr.fit(X_train, y_train[:,0])
# 对测试数据进行回归预测。
sgdr_y_predict = sgdr.predict(X_test)
ridge = Ridge(alpha=10)
# 使用训练数据进行参数估计。
ridge.fit(X_train, y_train[:,0])
# 对测试数据进行回归预测。
ridge_y_predict = ridge.predict(X_test)
# Lasso
lasso = Lasso(alpha=0.01)
# 使用训练数据进行参数估计。
lasso.fit(X_train, y_train[:,0])
# 对测试数据进行回归预测。
lasso_y_predict = lasso.predict(X_test)
return lr,sgdr,ridge,lasso,lr_y_predict,sgdr_y_predict,ridge_y_predict,lasso_y_predict
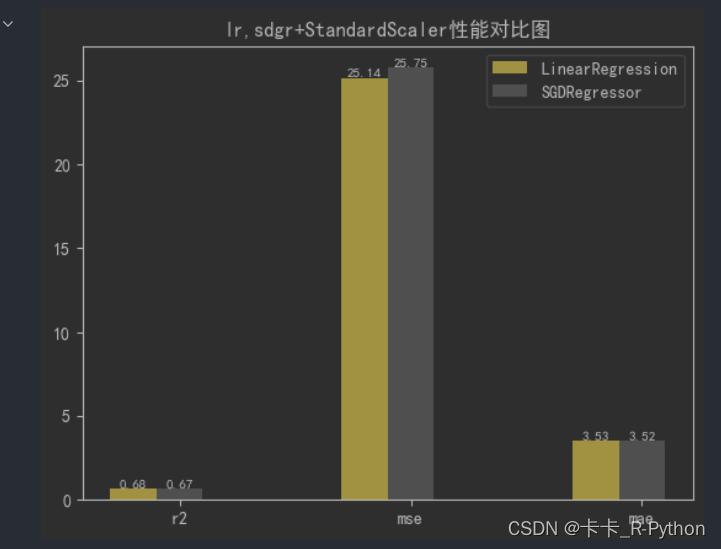
#显示柱状图的高度文本
for i in range(len(classes)):
plt.text(r2s_x[i],model1[i], model1[i],va="bottom",ha="center",fontsize=8)
plt.text(mess_x[i],model2[i], model2[i],va="bottom",ha="center",fontsize=8)
#plt.text(nmse_x[i],model3[i], model3[i],va="bottom",ha="center",fontsize=8)
#plt.text(mae_x[i],model4[i], model4[i],va="bottom",ha="center",fontsize=8)
#显示图例
plt.legend(loc="upper right")
plt.show()
#coding=gbk;
def plot_line(X,y,model,name):
#--------------------------------------------------------------
#z是我们生成的等差数列,用来画出线性模型的图形。
z=np.linspace(0,50,200).reshape(-1,1)
plt.scatter(y,ss_y.inverse_transform(model.predict(ss_X.transform(X)).reshape(len(X),-1)),c="orange",edgecolors='k')
plt.plot(z,z,c="k")
plt.xlabel('y')
plt.ylabel("y_hat")
plt.title(name)
plt.show()
lr,sgdr,ridge,lasso,lr_y_predict,sgdr_y_predict,ridge_y_predict,lasso_y_predict=train_model()
models=[lr,sgdr]
r2s=[]
mess=[]
maes=[]
nmse=[]
results=[]
plot_line(X,y,lr,'LinearRegression+'+ss)
plot_line(X,y,sgdr,'SGDRegressor+'+ss)
#plot_line(X,y,lasso,'lasso'+ss)
#plot_line(X,y,ridge,'ridge'+ss)
print("sgdr_y_predict")
print(sgdr_y_predict)
#evaluate(X_test,y_test,sgdr_y_predict,sgdr)
plot(results[0][1:4],results[1][1:4])
p=pd.DataFrame(result,columns=['波士顿房价预测值'])
p.to_csv('房价预测.csv')#波士顿房价预测值保存为csv文件