💬 写在前面:在函数式编程中,除了递归函数外,还经常使用高阶函数。高阶函数是指接收其他函数作为参数或返回另一个函数的函数。高阶函数通过抽象编程模式以实现重用,使程序可以在更高层次上进行编写。让我们重点看看常用的高阶函数,如map、filter 和 fold。
目录
0x00 map 函数
0x01 filter 函数
0x02 fold 函数
0x00 map 函数
下面定义的三个函数 inc_all、square_all 和 cube_all
分别是将给定列表的每个元素增加、平方和立方的函数。
let rec inc_all l =
match l with
| [] -> []
| hd::tl -> (hd+1)::(inc_all tl)
let rec square_all l =
match l with
| [] -> []
| hd::tl -> (hd*hd)::(square_all tl)
let rec cube_all l =
match l with
| [] -> []
| hd::tl -> (hd*hd*hd)::(cube_all tl)这些函数都是按照共同的模式定义的。
唯一的区别在于应用于列表各元素的操作。如果将这种操作一般称为 ,
那么上述三个函数所共享的编程模式可以用如下的高阶函数 map 来表示。
let rec map f l =
match l with
| [] -> []
| hd::tl -> (f hd)::(map f tl)
map 函数除了接收列表 之外,还接收一个函数
作为参数,
表示要应用于每个元素的操作。map 函数生成一个新列表,
其中列表 的每个元素
都被替换为 f a 的值。也就是说,
如果 是列表
,那么 map f l 将生成一个新列表
。
通过查看 map 的类型,我们可以理解它的大致含义:
![]()
所应用函数的类型是 ,表示接收一个 'a 类型的列表作为输入,
并生成一个 类型的列表作为输出。
一般来说,函数的类型可以被视为该函数所执行任务的摘要 (抽象) 。
利用高阶函数 map,可以简洁地定义上述三个函数如下:
let inc_all l = map (fun x -> x + 1) l
let square_all l = map (fun x -> x * x) l
let cub_all l = map (fun x -> x * x * x) l或者,可以省略共同的参数 ,定义如下:
let inc_all = map (fun x -> x + 1)
let square_all = map (fun x -> x * x)
let cub_all = map (fun x -> x * x * x)将其与前面的定义进行比较,可以发现,
使用 map 的定义使每个函数的含义在更高层次上显得更加清晰和直接。
例如,square_all 的含义直接表现为对列表 的每个元素应用函数 fun x -> x * x。
而如果不使用 map 而是递归编写的话,这种含义就隐藏在代码中,不会直接显现。
一个写得好的程序是其他人可以轻松理解的程序,因为即使不知道实现的细节,
也能在高层次上理解它。从这个角度来看,一种好的编程语言应当能够在更高层次上表达想法。
在函数式编程中,高阶函数在提升程序的抽象层次方面发挥了重要作用。
0x01 filter 函数
以下两个函数虽然执行的任务不同,但它们是按照相同的模式定义的:
let rec even l =
match l with
| [] -> []
| hd::tl ->
if hd mod 2 = 0 then hd::(even tl)
else even tl
let rec greater_than_five l =
match l with
| [] -> []
| hd::tl ->
if hd > 5 then hd::(greater_than_five tl)
else greater_than_five tl
even 函数从列表l中选择偶数,而 greater_than_five 函数选择大于 5 的数。
换句话说,它们都是从给定列表中选择满足特定条件的元素的函数,只是选择条件不同。
可以通过以下高阶函数来抽象化这种共同模式:
let rec filter p l =
match l with
| [] -> []
| hd::tl ->
if p hd then hd::(filter p tl)
else filter p tlfilter 函数接收一个函数 和一个列表
作为参数,
它的工作是收集列表l中满足函数 条件的元素。
这里函数 应该是一个返回布尔值的函数 (谓词) 。换言之,filter 的类型应该如下所示:
![]()
可以利用高阶函数 filter 来定义上述两个函数:
let even l = filter (fun x -> x mod 2 = 0) l
let greater_than_five l = filter (fun x -> x > 5) l0x02 fold 函数
在函数式编程中,最常用的高阶函数之一是 fold,让我们来比较一下下面这两个函数:
let rec sum l =
match l with
| [] -> 0
| hd::tl -> hd + (sum tl)
let rec prod l =
match l with
| [] -> 1
| hd::tl -> hd * (prod tl)这两个函数都遵循对给定列表的每个元素进行迭代并累积应用某种操作的模式。
例如,对于列表 ,应用上述两个函数的过程如下所示:
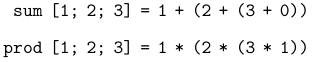
这两个函数的区别在于它们应用的累积操作和初始值。
例如,对于 sum 函数,操作符是 +,初始值是 0;
而对于 prod 函数,操作符是 *,初始值是 1。
我们可以定义一个高阶函数 fold_right,它接受这两个额外的参数,如下所示:
let rec fold_right f l a =
match l with
| [] -> a
| hd::tl -> f hd (fold_right f tl a)利用 fold_right 可以如下定义函数 sum 和 prod,其中 是累积操作,
是列表,
是初始值。
let sum lst = fold_right (fun x y -> x + y) lst 0
let prod lst = fold_right (fun x y -> x * y) lst 1每个函数的含义更直接地在更高级别上表达出来。sum 函数从初始值 0 开始,
对列表中的每个元素进行累加运算;而 prod 函数从初始值 1 开始,
对列表中的每个元素进行累乘运算。
考虑到 sum 和 prod 如何以尾递归函数的形式编写,其含义与上述示例相同:
let rec sum a l =
match l with
| [] -> a
| hd::tl -> sum (a + hd) tl
let rec prod a l =
match l with
| [] -> a
| hd::tl -> prod (a * hd) tl将定义了上述两个函数的共同模式的高阶函数称为 fold_left:
let rec fold_left f a l =
match l with
| [] -> a
| hd::tl -> fold_left f (f a hd) tl使用 fold_left 定义 sum 和 prod 的方式如下:
let sum a l = fold_left (fun x y -> x + y) a l
let prod a l = fold_left (fun x y -> x * y) a l让我们更详细地比较一下 fold_right 和 fold_left。
首先,它们的类型有所不同,如下所示:
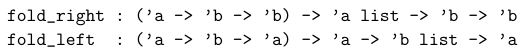
更重要的区别在于累积操作的方向不同。
fold_right 从列表的最后一个元素开始,向左依次累积。
![]()
相反,fold_left 从列表的最左边元素开始,向右依次累积:
![]()
因此,如果应用的操作 不满足结合律,两个结果可能会不同:
# fold_right (fun x y -> x - y) [1;2;3] 0;;
- : int 2
# fold_left (fun x y -> x - y) 0 [1;2;3];;
- : int = -6最后,fold_left 是尾递归函数。在列表长度较长的情况下,最好尽量使用 fold_left 。

📌 [ 笔者 ] 王亦优
📃 [ 更新 ] 2024.6.20
❌ [ 勘误 ] /* 暂无 */
📜 [ 声明 ] 由于作者水平有限,本文有错误和不准确之处在所难免,
本人也很想知道这些错误,恳望读者批评指正!| 📜 参考资料 - R. Neapolitan, Foundations of Algorithms (5th ed.), Jones & Bartlett, 2015. - T. Cormen《算法导论》(第三版),麻省理工学院出版社,2009年。 - T. Roughgarden, Algorithms Illuminated, Part 1~3, Soundlikeyourself Publishing, 2018. - J. Kleinberg&E. Tardos, Algorithm Design, Addison Wesley, 2005. - R. Sedgewick&K. Wayne,《算法》(第四版),Addison-Wesley,2011 - S. Dasgupta,《算法》,McGraw-Hill教育出版社,2006。 - S. Baase&A. Van Gelder, Computer Algorithms: 设计与分析简介》,Addison Wesley,2000。 - E. Horowitz,《C语言中的数据结构基础》,计算机科学出版社,1993 - S. Skiena, The Algorithm Design Manual (2nd ed.), Springer, 2008. - A. Aho, J. Hopcroft, and J. Ullman, Design and Analysis of Algorithms, Addison-Wesley, 1974. - M. Weiss, Data Structure and Algorithm Analysis in C (2nd ed.), Pearson, 1997. - A. Levitin, Introduction to the Design and Analysis of Algorithms, Addison Wesley, 2003. - A. Aho, J. Hopcroft, and J. Ullman, Data Structures and Algorithms, Addison-Wesley, 1983. - E. Horowitz, S. Sahni and S. Rajasekaran, Computer Algorithms/C++, Computer Science Press, 1997. - R. Sedgewick, Algorithms in C: 第1-4部分(第三版),Addison-Wesley,1998 - R. Sedgewick,《C语言中的算法》。第5部分(第3版),Addison-Wesley,2002 |