一、卡方检验

1.对400人进行问卷调查，询问对于教学改革的看法，调查结果如下表所示，请问不同学科不同性别的人意见是否相同。

学科	男生	女生
工科	80	40
理科	120	160

（性别，学科均无序分类=>卡方检验）（频数->加权个案）

1. 数据输入

首先，将数据输入到SPSS中。数据表格如下：

学科	性别	人数
工科	男生	80
工科	女生	40
理科	男生	120
理科	女生	160

2. 数据录入SPSS

1. 打开SPSS。
2. 在数据视图中，输入变量名：学科，性别，人数。
3. 输入上表中的数据。

3. 变量定义

在变量视图中，定义每个变量的属性：

• 学科和性别设为数值，定义好值。
• 人数设为数值（Numeric）。

4. 进行卡方检验

1. 在菜单栏中选择分析（Analyze）。

2. 选择描述统计（Descriptive Statistics），然后选择交叉表（Crosstabs）。

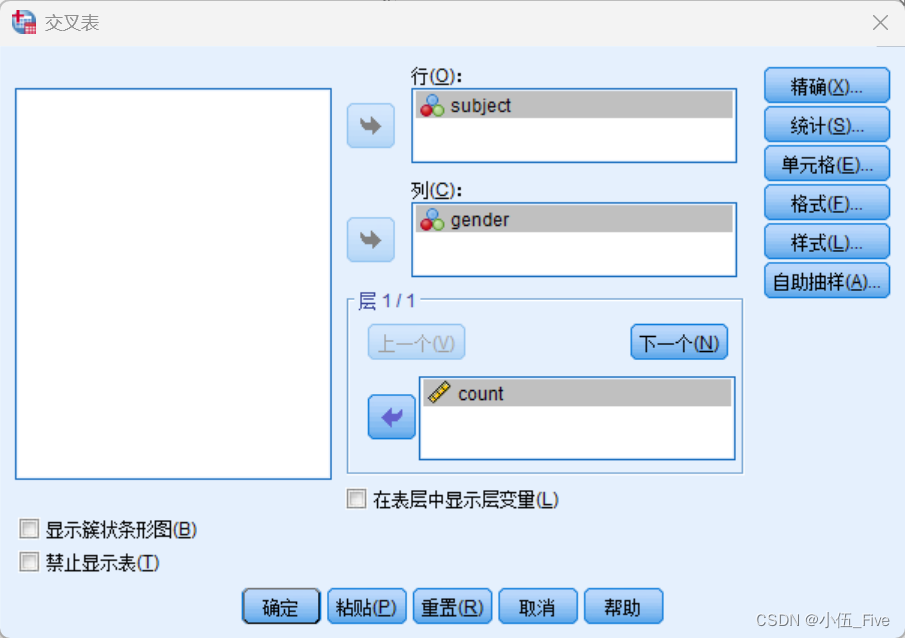
3. 在弹出的对话框中：

   • 将学科拖到行（Row(s)）区域。
   • 将性别拖到列（Column(s)）区域。
   • 将人数拖到层（Layer 1 of 1）区域。

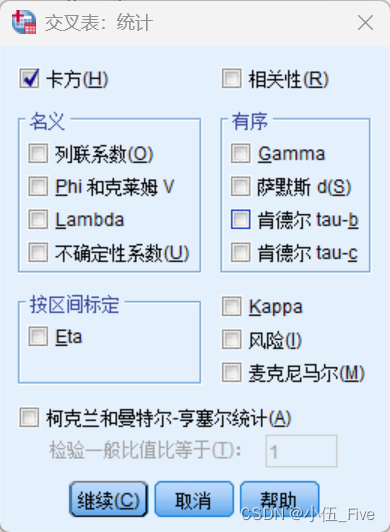
4.点击右下角的统计量（Statistics）按钮，勾选卡方（Chi-square），然后点击继续。

5.点击右下角的单元格（Cells）按钮，勾选观测值（Observed）和期望值（Expected），然后点击继续（Continue）。

6.点击确定（OK），SPSS将会生成结果。

5. 结果解释

结果会显示在输出窗口中，主要关注以下几点：

• 卡方检验表格：

  • 查看Pearson 卡方的显著性（Asymp. Sig. (2-sided)）值（即p值）。
  • 如果p值小于0.05，则认为不同学科和性别的学生对教学改革的看法存在显著差异。

• 交叉表（Crosstabulation）表格：

  • 查看观测频数（Observed N）和期望频数（Expected N）的差异。

6. 具体结果解释

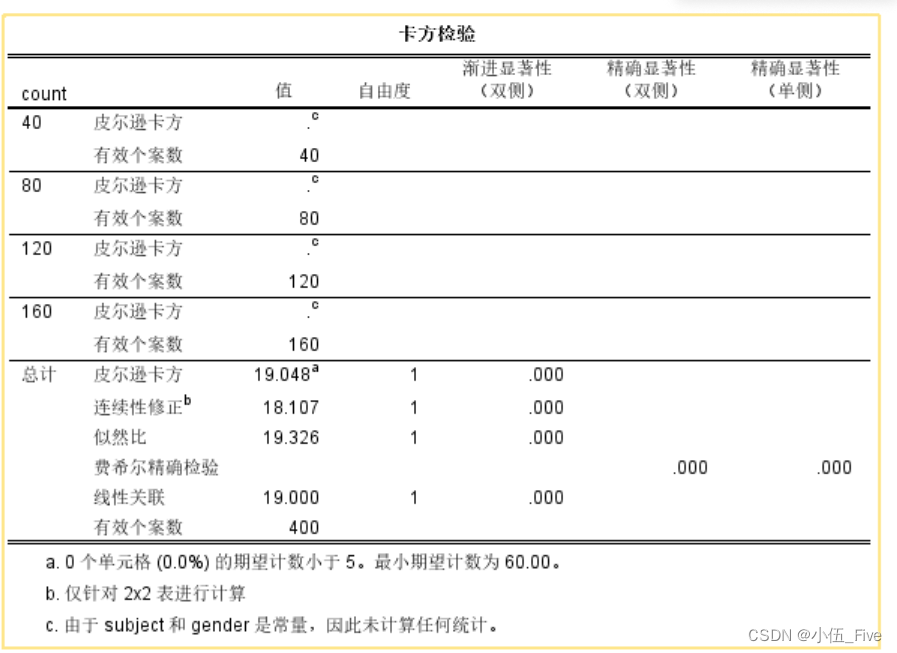
1. 样本数和有效个案数

在数据中，我们看到不同样本数（40, 80, 120, 160和400）的情况下，对皮尔逊卡方统计量进行了分析。所有样本的有效个案数为400。

2. 皮尔逊卡方统计量

总计部分的皮尔逊卡方统计量为19.048，自由度为1，渐进显著性（双侧）为.000。这意味着在这些数据中，我们有非常强的证据拒绝原假设（即变量是独立的），认为变量之间有显著关系。皮尔逊卡方值为19.048，且其显著性水平（p值）为.000，这表明结果在统计上显著。

3. 连续性修正

连续性修正是专门为2x2表格计算的修正统计量。在本例中，连续性修正的卡方统计量为18.107，自由度为1，显著性水平为.000。这进一步支持了皮尔逊卡方的结论，表明变量之间存在显著关系。

4. 似然比

似然比检验是一种与卡方检验类似的检验方法，但它基于最大似然估计。在这组数据中，似然比为19.326，自由度为1，显著性水平为.000。这同样表明了变量之间存在显著关系。

5. 费希尔精确检验

费希尔精确检验是一种非参数检验，特别适用于小样本数据。在这里，费希尔精确检验的显著性（双侧和单侧）均为.000，进一步确认了变量之间的显著关系。

6. 线性关联

线性关联检验值为19.000，自由度为1，显著性水平为.000。这也是对变量间显著关系的有力支持。

1. 皮尔逊卡方检验、连续性修正、似然比检验、费希尔精确检验和线性关联检验均表明变量之间存在显著关系。
2. 所有检验的显著性水平均为.000，意味着结果非常显著。
3. 数据满足卡方检验的基本要求（期望计数大于5）

二、单因素方差分析

某公司想比较五种销售方法有无显著的效果差异，从应聘人员中随机挑选分为为五组，每组用一种推销方法培训。一段时期后得到各组销售额如下表所示：（有五组，每组为连续性变量=>单因素方差分析）

（1）分析这五种推销方式是否存在显著差异。

（2）绘制相关均值图，并说明利用合适的方法进行多重比较检验，说明那组推销方式最好？

（1）分析五种推销方式是否存在显著差异

数据输入

步骤1：输入数据

1. 打开SPSS软件。
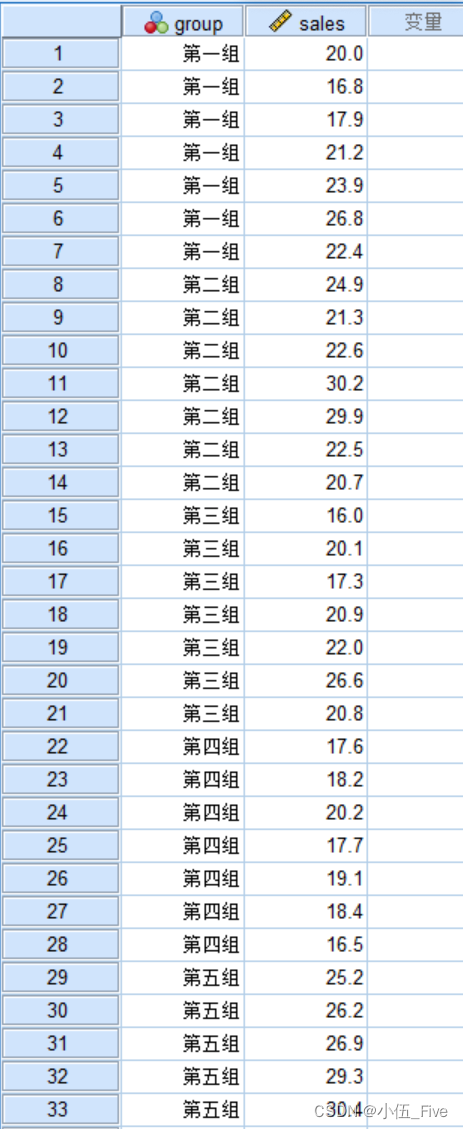
2. 在“数据视图”中，手动输入数据。数据格式应该有两列：一列表示组别（可以用1到5表示），一列表示销售额。

组别	销售额
1	20.0
1	16.8
1	17.9
1	21.2
1	23.9
1	26.8
1	22.4
2	24.9
2	21.3
2	22.6
2	30.2
2	29.9
2	22.5
2	20.7
3	16.0
3	20.1
3	17.3
3	20.9
3	22.0
3	26.8
3	20.8
4	17.5
4	18.2
4	20.2
4	17.7
4	19.1
4	18.4
4	16.5
5	25.2
5	26.2
5	26.9
5	29.3
5	30.4
5	29.7
5	28.3

单因素方差分析

步骤2：执行单因素方差分析

1. 选择菜单栏中的 分析。
2. 选择 比较均值，然后选择 单因素方差分析。
3. 将“销售额”变量拖到 因变量列表 中。
4. 将“组别”变量拖到 因子 框中。
5. 点击 选项 按钮，勾选 描述 和 方差齐性检验，然后点击 继续。
6. 点击 事后 按钮，选择LSD 和 塔姆黑尼，然后点击 继续。
7. 点击 确定 运行分析。

结果解释

运行ANOVA后，您将得到以下几个重要结果：

1. 描述性统计：显示每组的样本数、均值、标准差等信息。
2. 方差齐性检验：Levene检验结果，用于检验各组方差是否相等。
3. 方差分析表：
   • 组间：表示各组均值的差异。
   • 组内：表示组内数据的变异。
   • F 值和 Sig.（p值）：用于判断是否存在显著差异。

如果 Sig.（p值）小于显著性水平（通常为0.05），则拒绝原假设，认为至少有两组的均值存在显著差异。

（2）绘制相关均值图，并进行多重比较检验

均值图绘制

步骤3：绘制均值图

1. 选择菜单栏中的 图表。
2. 选择 图表生成器。
3. 在弹出的窗口中，选择 箱形图。
4. 将“销售额”拖到 Y 轴 区域，将“组别”拖到 X 轴 区域。
5. 点击 确定 绘制箱线图。

多重比较检验

在进行ANOVA分析时，我们已经选择了LSD 和塔姆黑尼 方法进行事后检验。检验将比较每一对组别之间的均值差异，并给出显著性水平。

步骤4：查看多重比较检验结果

1. 在ANOVA结果窗口中，找到 多重比较 表格。
2. 查看每对组别之间的比较结果，特别关注 Sig.（p值）。如果 p值小于0.05，则表明这对组别之间的均值差异显著。

解释哪组推销方式最好

多重比较的结果包括LSD（最小显著差异检验）和塔姆黑尼（Tamhane's T2）检验。以下是对这些结果的详细解释：

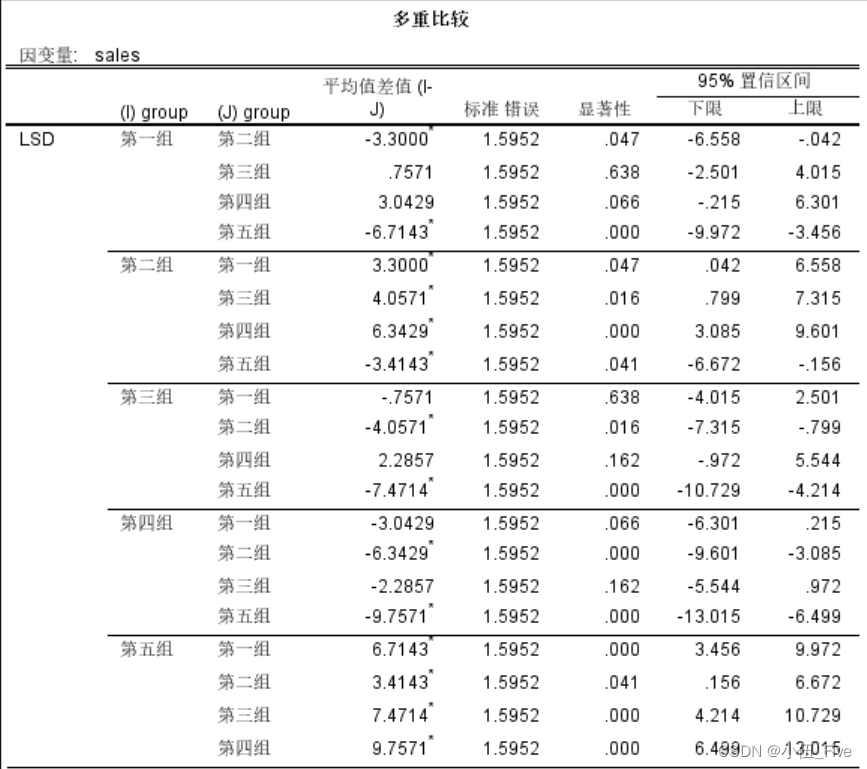
LSD检验结果

LSD检验比较了每对组之间的均值差异，并指出哪些差异是显著的（显著性水平为0.05）。结果显示如下：

• 第一组 vs 第二组：均值差异为-3.3000，显著性为0.047。这表明第一组的平均销售额显著低于第二组。
• 第一组 vs 第五组：均值差异为-6.7143，显著性为0.000。这表明第一组的平均销售额显著低于第五组。
• 第二组 vs 第三组：均值差异为4.0571，显著性为0.016。这表明第二组的平均销售额显著高于第三组。
• 第二组 vs 第四组：均值差异为6.3429，显著性为0.000。这表明第二组的平均销售额显著高于第四组。
• 第二组 vs 第五组：均值差异为-3.4143，显著性为0.041。这表明第二组的平均销售额显著低于第五组。
• 第三组 vs 第五组：均值差异为-7.4714，显著性为0.000。这表明第三组的平均销售额显著低于第五组。
• 第四组 vs 第五组：均值差异为-9.7571，显著性为0.000。这表明第四组的平均销售额显著低于第五组。

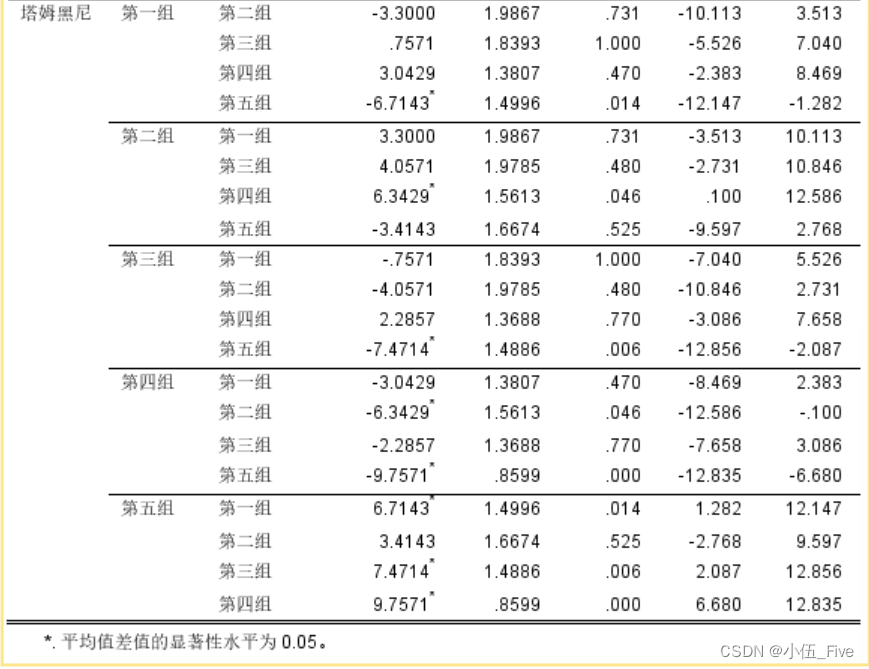
塔姆黑尼检验结果

塔姆黑尼检验结果用于当组间方差不等时的多重比较。结果如下：

• 第一组 vs 第五组：均值差异为-6.7143，显著性为0.014。这表明第一组的平均销售额显著低于第五组。
• 第二组 vs 第四组：均值差异为6.3429，显著性为0.046。这表明第二组的平均销售额显著高于第四组。
• 第三组 vs 第五组：均值差异为-7.4714，显著性为0.006。这表明第三组的平均销售额显著低于第五组。
• 第四组 vs 第五组：均值差异为-9.7571，显著性为0.000。这表明第四组的平均销售额显著低于第五组。

哪组推销方式最好

根据均值差异和显著性检验结果，我们可以得出以下结论：

1. 第五组的推销方式最好：因为第五组的平均销售额显著高于其他所有组。在LSD和塔姆黑尼检验中，所有与第五组的比较中，均显示其销售额显著高于其他组。

2. 第二组的推销方式次之：在LSD检验中，第二组的平均销售额显著高于第一组、第三组和第四组，且在塔姆黑尼检验中，第二组的销售额显著高于第四组。

具体分析

• 第一组：相对较差，销售额显著低于第二组和第五组。
• 第二组：表现较好，销售额显著高于第一组、第三组和第四组，但低于第五组。
• 第三组：销售额显著低于第二组和第五组。
• 第四组：销售额显著低于第二组和第五组。
• 第五组：表现最佳，销售额显著高于所有其他组。