AVL树模拟

news2024/10/5 17:22:48

1.概念

虽然二叉搜索树可以缩短查找的效率，但如果数据有序或者接近有序时二叉搜索树树将退化为单支树，查找元素相当于在顺序表中搜索元素，效率低下。AVL
树是具有一下性质的二叉搜索树：        

        1.它的左右子树都是AVL树

        2.左右子树的高度差的绝对值不超过1

如果一个二叉搜索树是高度平衡的，它就是AVL树。如果它有n个节点，其高度可保持在log N,搜索时间复杂度为O(log N)；

2.节点定义

template<class T>
struct AVLTreeNode
{
	AVLTreeNode(T key)
		:_bf(0), _key(key)
	{}

	AVLTreeNode* _left = nullptr;
	AVLTreeNode* _right = nullptr;
	AVLTreeNode* _parent = nullptr;
	int _bf;					//平衡因子
	T _key;
};

3.AVL插入

AVL树的插入就是在二叉搜索树的基础上引入了平衡因子，因此AVL树也可以看成是二叉搜索树。

AVL树的插入过程可以分为两部分：

        1.按照二叉搜索树的方式插入新节点

        2.调整平衡因子

3.1 按照二叉搜索树的方式插入新的节点

 

bool Insert(T key)
{
	Node* newnode = new Node(key);
	if (_root == nullptr)
	{
		_root = newnode;
		return true;
	}
	Node* cur = _root;
	Node* parent = nullptr;
	//寻找插入位置
	while (cur)
	{
		if (key > cur->_key)
		{
			parent = cur;
			cur = cur->_right;
		}
		else if (key < cur->_key)
		{
			parent = cur;
			cur = cur->_left;
		}
		else return false;
	}
	//插入新的节点
	newnode->_parent = parent;
	if (key < parent->_key) parent->_left = newnode;
	else parent->_right = newnode;
}

3.2调整平衡因子

新节点插入后，AVL树的平衡性可能遭到破坏，因此就需要更新平衡因子，并检测是否破坏了AVL树的平衡性

当newnode插入后，parent的平衡因子一点需要调整，在插入之前parent的平衡因子分为三种情况：-1，0，1。

调整方式分为以下两种：

        当新节点插入到parent左侧时，parent平衡因子-1；

        当新节点插入到parent右侧时，parent平衡因子+1；

此时parent的平衡因子有以下三种情况：0，正负1，正负2

        1.如果此时的平衡因子为0，说明插入新的节点后parent平衡了，满足AVL树的性质，无需继续向上调整。

        2.如果此时平衡因子为正负1，说明插入新的节点后parent为根的树高度增加，需要继续向上调整。

        3.如果此时平衡因子为正负2，说明parent违反了AVL树的性质，需要对其经行旋转处理。

cur = newnode;
while (parent)
{
    //更新平衡因子
	if (cur == parent->_left) parent->_bf--;
	else parent->_bf++;

	//检查平衡因子状态

	if (parent->_bf == 0) break;
	else if (parent->_bf == 1 || parent->_bf == -1)
	{
		cur = parent;
		parent = parent->_parent;
	}
	//不平衡，旋转
	else if (parent->_bf == 2 || parent->_bf == -2)
	{
		if (parent->_bf == 2)
		{
            //...
		}
		else
		{
            //...
		}
		break;
	}
	else
	{
		cout << "error: _bf";
		break;
	}
}

4. AVL树的旋转

 上图在插入前，AVL树是平衡的，新节点插入到30的左子树(注意：此处不是左孩子)中，30左 子树增加了一层，导致以60为根的二叉树不平衡。

要让60平衡，只能将60左子树的高度减少一层，右子树增加一层，  即将左子树往上提，这样60转下来，因为60比30大，只能将其放在30的右子树，而如果30有右子树，右子树根的值一定大于30，小于60，只能将其放在60的左子树，旋转完成后，更新节点 的平衡因子即可。

在旋转过程中，有以下几种情况需要考虑：  1. 30节点的右孩子可能存在，也可能不存在  2. 60可能是根节点，也可能是子树如果是根节点，旋转完成后，要更新根节点如果是子树，可能是某个节点的左子树，也可能是右子树

a.右单旋


void _RotateR(Node* pParent)
{
	// pSubL: pParent的左孩子
	// pSubLR: pParent左孩子的右孩子，注意：该
	PNode* pSubL = pParent->_pLeft;
	PNode* pSubLR = pSubL->_pRight;

	// 旋转完成之后，30的右孩子作为双亲的左孩子
	pParent->_pLeft = pSubLR;

	// 如果30的左孩子的右孩子存在，更新亲双亲
	if (pSubLR) pSubLR->_pParent = pParent;
	// 60 作为 30的右孩子


	// 因为60可能是棵子树，因此在更新其双亲前必须先保存60的双亲
	PNode pPParent = pParent->_pParent;

	// 更新60的双亲
	pParent->_pParent = pSubL;

	// 更新30的双亲
	pSubL->_pParent = pPParent;

	// 如果60是根节点，根新指向根节点的指针
	if (NULL == pPParent)
	{
		_pRoot = pSubL;
		pSubL->_pParent = NULL;
	}
	else
	{
		// 如果60是子树，可能是其双亲的左子树，也可能是右子树
		if (pPParent->_pLeft == pParent)
			pPParent->_pLeft = pSubL;
		else
			pPParent->_pRight = pSubL;
	}

	// 根据调整后的结构更新部分节点的平衡因子
	pParent->_bf = pSubL->_bf = 0;
}

b.左单旋 

 

具体细节与右单旋一致。

void _RotateL(Node* pParent)
{
	Node* RSub = pParent->_right;
	Node* RSubL = RSub->_left;
	Node* pPParent = pParent->_parent;


	if (RSubL) RSubL->_parent = pParent;
	pParent->_right = RSubL;

	RSub->_left = pParent;
	pParent->_parent = RSub;
	RSub->_parent = pPParent;

	if (pParent == _root) _root = RSub;
	else
	{
		if (pPParent->_left == pParent) pPParent->_left = RSub;
		else pPParent->_right = RSub;
	}
	//更新平衡因子
	RSub->_bf = pParent->_bf = 0;
}

c.先左旋在右旋

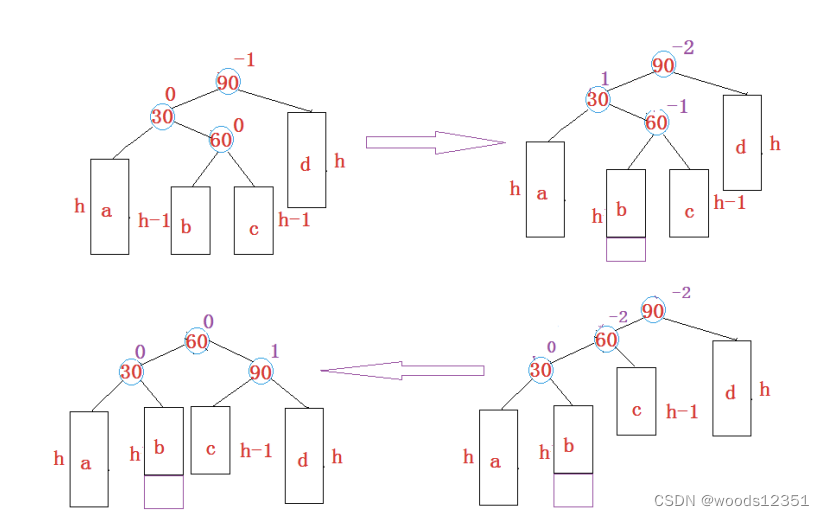
将双旋变成单旋后再旋转，即：先对30进行左单旋，然后再对90进行右单旋，旋转完成后再 考虑平衡因子的更新。

 

// 旋转之前，60的平衡因子可能是-1/0/1，旋转完成之后，根据情况对其他节点的平衡因子进
//行调整
void _RotateLR(PNode pParent)
{
	PNode pSubL = pParent->_pLeft;
	PNode pSubLR = pSubL->_pRight;

	// 旋转之前，保存pSubLR的平衡因子，旋转完成之后，需要根据该平衡因子来调整其他节
	//点的平衡因子
		int bf = pSubLR->_bf;

	// 先对30进行左单旋
	_RotateL(pParent->_pLeft);

	// 再对90进行右单旋
	_RotateR(pParent);
	if (1 == bf)
		pSubL->_bf = -1;
	else if (-1 == bf)
		pParent->_bf = 1;
}

d. 先右旋在左旋

void _RotateRL(Node* pParent)
{
	Node* RSub = pParent->_right;
	Node* RSubL = RSub->_left;
	int bf = RSubL->_bf;

	_RotateR(RSub);
	_RotateL(pParent);
	RSub->_bf = 0;
	if (bf == 1)
	{
		RSub->_bf = 0;
		pParent->_bf = -1;
	}
	else if (bf == -1)
	{
		pParent->_bf = 0;
		RSub->_bf = 1;
	}
	else
	{
		RSub->_bf = pParent->_bf = 0;
	}
}

总结：

加入以parent为根的子树不平衡，即以parent的平衡因子为2或-2，分别考虑以下情况

        1.parent的平衡因子为2，说明parent的右子树高，设parent的右子树的根为RSub

                当RSub的平衡因子为1时，执行左单旋，

                当RSub的平衡因子为-1时，执行左右双旋。

        2.parent的平衡因子为-2 ，说明parent的左子树高，设parent的左子树的根为LSub

                当LSub的平衡因子为-1时，执行右单旋。

                当LSub的平衡因子为1时，执行做单旋。

当旋转接完成后，parent为根的子树高度已经降低，以及平衡，无需向上更新。

5.AVL树的验证

AVL树实在二叉搜索树的基础上加了平衡性的限制，因此要验证AVL树可以分为两步

        1.验证其为二叉搜索树

                如果中序遍历结果为有序，则为二叉搜索树

        2.验证其为平衡树

                1.每个子树高度差的绝对值不超过1

                2.节点平衡因子正确

void InOrder()
{
	_InOrder(_root);
}

int GETHeight()
{
	return _GETHeight(_root);
}

bool IsBalance()
{
	return _isBalance(_root);
}	

bool _isBalance(Node* root)
{
	if (root->_bf >= 2 || root->_bf <= -1) return false;
	int HeightLeft = _GETHeight(root->_left);
	int HeightRight = _GETHeight(root->_right);
	if (abs(HeightRight - HeightLeft) > 1) return false;
	return _isBalance(root->_left) && _isBalance(root->_right);
}
int _GETHeight(Node* root)
{
	if (root == nullptr) return 0;
	return max(_GETHeight(root->_left), _GETHeight(root->_right)) + 1;
}
void _InOrder(Node* root)
{
	if (root == nullptr) return;
	_InOrder(root->_left);
	cout << root->_key << " ";
	_InOrder(root->_right);
}

测试代码 

void test_AVL01()
{
	int a[] = { 8, 3, 1, 10, 6, 4, 7, 14, 13 };
	//int a[] = { 4, 2, 6, 1, 3, 5, 15, 7, 16, 14 };
	AVLTree<int> t1;
	for (auto e : a)
	{

		t1.Insert(e);

		//cout << "Insert:" << e << "->" << t1.IsBalance() << endl;
	}
	cout << t1.GETHeight() << endl;
	t1.InOrder();

	//cout << t1.IsBalance() << endl;
}

6.AVL树模拟代码

#pragma once

template<class T>
struct AVLTreeNode
{
	AVLTreeNode(T key)
		:_bf(0), _key(key)
	{}

	AVLTreeNode* _left = nullptr;
	AVLTreeNode* _right = nullptr;
	AVLTreeNode* _parent = nullptr;
	int _bf;					//平衡因子
	T _key;
};

template<class T>
class AVLTree
{
	typedef AVLTreeNode<T> Node;
public:
	bool Insert(T key)
	{
		Node* newnode = new Node(key);
		if (_root == nullptr)
		{
			_root = newnode;
			return true;
		}
		Node* cur = _root;
		Node* parent = nullptr;
		//寻找插入位置
		while (cur)
		{
			if (key > cur->_key)
			{
				parent = cur;
				cur = cur->_right;
			}
			else if (key < cur->_key)
			{
				parent = cur;
				cur = cur->_left;
			}
			else return false;
		}
		//插入新的节点
		newnode->_parent = parent;
		if (key < parent->_key) parent->_left = newnode;
		else parent->_right = newnode;

		//更新平衡因子
		//插入后AVL树平衡，无需调整
		//插入后AVL树高度增加，继续向上调整
		cur = newnode;
		while (parent)
		{
			if (cur == parent->_left) parent->_bf--;
			else parent->_bf++;

			//检查平衡因子状态

			if (parent->_bf == 0) break;
			else if (parent->_bf == 1 || parent->_bf == -1)
			{
				cur = parent;
				parent = parent->_parent;
			}
			//不平衡，旋转
			else if (parent->_bf == 2 || parent->_bf == -2)
			{
				if (parent->_bf == 2)
				{
					//左单旋
					if (parent->_right->_bf == 1)
					{
						_RotateL(parent);
					}
					else
					{
						_RotateRL(parent);
					}
				}
				else
				{
					//右单旋
					if (parent->_left->_bf == -1)
					{
						_RotateR(parent);
					}
					else
					{
						_RotateLR(parent);
					}
				}
				break;
			}
			else
			{
				cout << "error: _bf";
				break;
			}
		}
		return true;
	}

	Node* Find(const T& key)
	{
		Node* cur = _root;
		while (cur)
		{
			if (key > cur->_key) cur = cur->_right;
			else if (key < cur->_key) cur = cur->_left;
			else return cur;
		}
		return nullptr;
	}
	size_t Size()
	{
		return _Size(_root);
	}
	void InOrder()
	{
		_InOrder(_root);
	}

	int GETHeight()
	{
		return _GETHeight(_root);
	}

	bool IsBalance()
	{
		return _isBalance(_root);
	}	
private:
	
	
	bool _isBalance(Node* root)
	{
		if (root->_bf >= 2 || root->_bf <= -1) return false;
		int HeightLeft = _GETHeight(root->_left);
		int HeightRight = _GETHeight(root->_right);
		if (abs(HeightRight - HeightLeft) > 1) return false;
		return _isBalance(root->_left) && _isBalance(root->_right);
	}
	int _GETHeight(Node* root)
	{
		if (root == nullptr) return 0;
		return max(_GETHeight(root->_left), _GETHeight(root->_right)) + 1;
	}
	void _InOrder(Node* root)
	{
		if (root == nullptr) return;
		_InOrder(root->_left);
		cout << root->_key << " ";
		_InOrder(root->_right);
	}
	size_t _Size(Node* root)
	{
		if (root == nullptr) return 0;
		size_t SizeLeft = _Size(root->_left);
		size_t SizeRight = _Size(root->_right);
		return SizeLeft + SizeRight + 1;
	}
	//右旋
	void _RotateR(Node* pParent)
	{
		Node* LSub = pParent->_left;
		Node* LSubR = LSub->_right;
		Node* pPParent = pParent->_parent;


		if(LSubR)LSubR->_parent = pParent;
		pParent->_left = LSubR;

		LSub->_right = pParent;
		pParent->_parent = LSub;
		LSub->_parent = pPParent;

		if (pParent == _root) _root = LSub;
		else
		{
			if (pPParent->_left == pParent) pPParent->_left = LSub;
			else pPParent->_right = LSub;
		}
		//更新平衡因子
		LSub->_bf = pParent->_bf = 0;
	}

	//左旋
	void _RotateL(Node* pParent)
	{
		Node* RSub = pParent->_right;
		Node* RSubL = RSub->_left;
		Node* pPParent = pParent->_parent;


		if (RSubL) RSubL->_parent = pParent;
		pParent->_right = RSubL;

		RSub->_left = pParent;
		pParent->_parent = RSub;
		RSub->_parent = pPParent;

		if (pParent == _root) _root = RSub;
		else
		{
			if (pPParent->_left == pParent) pPParent->_left = RSub;
			else pPParent->_right = RSub;
		}
		//更新平衡因子
		RSub->_bf = pParent->_bf = 0;
	}
	void _RotateRL(Node* pParent)
	{
		Node* RSub = pParent->_right;
		Node* RSubL = RSub->_left;
		int bf = RSubL->_bf;

		_RotateR(RSub);
		_RotateL(pParent);
		RSub->_bf = 0;
		if (bf == 1)
		{
			RSub->_bf = 0;
			pParent->_bf = -1;
		}
		else if (bf == -1)
		{
			pParent->_bf = 0;
			RSub->_bf = 1;
		}
		else
		{
			RSub->_bf = pParent->_bf = 0;
		}
	}

	void _RotateLR(Node* pParent)
	{
		Node* LSub = pParent->_left;
		Node* LSubR = LSub->_right;
		int bf = LSubR->_bf;

		_RotateL(LSub);
		_RotateR(pParent);

		LSub->_bf = 0;
		if (bf == 0)
		{
			LSubR->_bf = LSubR->_bf = 0;
		}
		else if (bf == 1)
		{
			LSub->_bf = -1;
			pParent->_bf = 0;
		}
		else if (bf == -1)
		{
			LSub->_bf = 0;
			pParent->_bf = 1;
		}

	}

private:
	Node* _root = nullptr;
};


void test_AVL01()
{
	int a[] = { 8, 3, 1, 10, 6, 4, 7, 14, 13 };
	//int a[] = { 4, 2, 6, 1, 3, 5, 15, 7, 16, 14 };
	AVLTree<int> t1;
	for (auto e : a)
	{
		int i = 1;


		t1.Insert(e);

		//cout << "Insert:" << e << "->" << t1.IsBalance() << endl;
	}
	cout << t1.GETHeight() << endl;
	t1.InOrder();

	//cout << t1.IsBalance() << endl;
}

void test_AVL02()
{
	const int N = 10000000;
	vector<int> v;
	v.reserve(N);
	srand(time(0));

	for (size_t i = 0; i < N; i++)
	{
		v.push_back(rand() + i);
		//cout << v.back() << endl;
	}

	size_t begin2 = clock();
	AVLTree<int> t;
	for (auto e : v)
	{
		t.Insert(e);
		//cout << "Insert:" << e << "->" << t.IsBalance() << endl;
	}
	size_t end2 = clock();

	cout << "Insert:" << end2 - begin2 << endl;
	//cout << t.IsBalance() << endl;

	cout << "Height:" << t.GETHeight() << endl;
	cout << "Size:" << t.Size() << endl;

	size_t begin1 = clock();
	// 确定在的值
	for (auto e : v)
	{
		t.Find(e);
	}

	// 随机值
	/*for (size_t i = 0; i < N; i++)
	{
		t.Find((rand() + i));
	}*/

	size_t end1 = clock();

	cout << "Find:" << end1 - begin1 << endl;
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1876819.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

[Go 微服务] Kratos 使用的简单总结

[Go 微服务] Kratos 使用的简单总结

文章目录 1.Kratos 简介2.传输协议3.日志4.错误处理5.配置管理6.wire 1.Kratos 简介 Kratos并不绑定于特定的基础设施&#xff0c;不限定于某种注册中心&#xff0c;或数据库ORM等&#xff0c;所以您可以十分轻松地将任意库集成进项目里&#xff0c;与Kratos共同运作。 API -&…
阅读更多...
《mysql篇》--查询(进阶)

《mysql篇》--查询(进阶)

目录 将查询结果作为插入数据 聚合查询 聚合函数 count sum group by子句 having 联合查询 笛卡尔积 多表查询 join..on实现多表查询 内连接 外连接 自连接 子查询 合并查询 将查询结果作为插入数据 Insert into 表2 select * from 表1//将表1的查询数据插入…
阅读更多...
【UE 网络】专用服务器和多个客户端加入游戏会话的过程，以及GameMode、PlayerController、Pawn的创建流程

【UE 网络】专用服务器和多个客户端加入游戏会话的过程，以及GameMode、PlayerController、Pawn的创建流程

目录 0 引言1 多人游戏会话1.1 Why&#xff1f;为什么要有这个1.2 How&#xff1f;怎么使用&#xff1f; 2 加入游戏会话的流程总结 &#x1f64b;‍♂️ 作者&#xff1a;海码007&#x1f4dc; 专栏&#xff1a;UE虚幻引擎专栏&#x1f4a5; 标题&#xff1a;【UE 网络】在网络…
阅读更多...
爬坑之 [‘NODE_ENV‘ 不是内部或外部命令，也不是可运行的程序 或批处理文件。]

爬坑之 [‘NODE_ENV‘ 不是内部或外部命令，也不是可运行的程序 或批处理文件。]

在package.json中配置如下&#xff1a; 执行npm run dev启动 报错&#xff1a; 实际上, NODE_ENVdevelopment webpack-dev-server 这条脚本会合并为两条命令执行&#xff0c; 分别为&#xff1a; NODE_EVNdevelopment webpack-dev-server 这种写法在cmd中是不被支持的 解决…
阅读更多...
Bootstrap更改默认的“请在电子邮件地址中包含@”

Bootstrap更改默认的“请在电子邮件地址中包含@”

摘要&#xff1a; 今天开发一个外贸系统&#xff0c;必须全部英文的&#xff0c;但是使用到bootatrp 4的input标签的type"email"输入没有含“”符号时会提示&#xff1a;“请在电子邮件地址中包含”中文提示&#xff01;一开始以为是中国下载的谷歌是浏览器自带的提示…
阅读更多...
计算机网络知识整理笔记

计算机网络知识整理笔记

目录 1.对网络协议的分层&#xff1f; 2.TCP/IP和UDP之间的区别&#xff1f; 3.建立TCP连接的三次握手&#xff1f; 4.断开TCP连接的四次挥手&#xff1f; 5.TCP协议如何保证可靠性传输&#xff1f; 6.什么是TCP的拥塞控制&#xff1f; 7.什么是HTTP协议&#xff1f; 8…
阅读更多...
停车场智能化管理：车位引导系统实现车位资源优化与数据分析

停车场智能化管理：车位引导系统实现车位资源优化与数据分析

随着城市汽车保有量的不断增长&#xff0c;停车难问题日益凸显。尤其是在高峰时段&#xff0c;寻找停车位和取车成为了许多车主的头疼问题。为了解决这一难题&#xff0c;维小帮智能车位引导系统应运而生&#xff0c;它利用先进的技术手段&#xff0c;帮助车主快速找到停车位&a…
阅读更多...
【计算机图形学】期末考试知识点汇总

【计算机图形学】期末考试知识点汇总

文章目录 第一章计算机图形学概述计算机图形学的定义计算机图形学的应用计算机图形学 vs 图像处理 vs模式识别图形显示器的发展及工作原理理解三维渲染管线 第二章 基本图元的扫描转换扫描转换直线的扫描转换DDA算法Bresenham算法中点画线算法圆的扫描转换中点画圆算法反走样 第…
阅读更多...
2024steam夏促商店打不开、steam活动加载不了解决方法一览

2024steam夏促商店打不开、steam活动加载不了解决方法一览

今年的夏促终于开始了!目前可以看到很多精品小游戏在促销列表内&#xff0c;活动正式开启后还不知道又会是怎样的一幅场景。因为每年夏促都会有不少刚高考完的新手加入&#xff0c;遇到常见的steam商店打不开、活动页面不加载等问题不知道怎么解决。所以这里给大家准备了几种常…
阅读更多...
从零创建深度学习张量库，支持gpu并行与自动微分

从零创建深度学习张量库，支持gpu并行与自动微分

多年来&#xff0c;我一直在使用 PyTorch 构建和训练深度学习模型。尽管我已经学会了它的语法和规则&#xff0c;但总有一些东西激起了我的好奇心&#xff1a;这些操作内部发生了什么&#xff1f;这一切是如何运作的&#xff1f; 如果你已经到这里&#xff0c;你可能也有同样的…
阅读更多...
mybatis的高级映射

mybatis的高级映射

mybatis的高级映射(重点) 表与表之间的关系&#xff1a; 一对一关系&#xff1a; 栗子&#xff1a;一个人对应一个身份证号 一对多关系&#xff1a; 栗子&#xff1a;一个用户可以有多个订单 1. 分析需求&…
阅读更多...
权限维持-域环境单机版---粘滞键屏保登录

权限维持-域环境单机版---粘滞键屏保登录

免责声明;本文仅做技术交流与学习,,, 目录 粘滞键: 粘滞键位置&#xff1a; 屏保&登录: 1、WinLogon配合无文件落地上线 结合ps命令: 2、屏幕保护生效后执行后门 粘滞键: Windows维权之粘滞键项维权-腾讯云开发者社区-腾讯云 (tencent.com) 系统自带的辅助功能进行替…
阅读更多...
LNBxx21的功能

LNBxx21的功能

LNBxx21功能&#xff1a; LNBxx21 家族是为卫星LNB模块供电/连接LNB块与接收机的集成化解决方案。LNBxx21的很多功能可以让LNB电源/接口符合国际标准&#xff0c;此外&#xff0c;模块内还包括一个I2C总线接口&#xff0c;因为集成了一个升压直流-直流控制器&#xff0c;所以可…
阅读更多...
MySQL InnoDB支持几种行格式

MySQL InnoDB支持几种行格式

数据库表的行格式决定了一行数据是如何进行物理存储的&#xff0c;进而影响查询和DML操作的性能。 在InnoDB中&#xff0c;常见的行格式有4种&#xff1a; 1、COMPACT&#xff1a;是MySQL 5.0之前的默认格式&#xff0c;除了保存字段值外&#xff0c;还会利用空值列表保存null…
阅读更多...
zabbix-agent2启动失败报错Unit zabbix-agent2.service entered failed state.

zabbix-agent2启动失败报错Unit zabbix-agent2.service entered failed state.

文章目录 1&#xff0c;用systemctl status zabbix-agent2查看报错状态2&#xff0c;用journalctl -xe查看一下报错日志3&#xff0c;再看一下zabbix的日志。4&#xff0c;错误修改5&#xff0c; 再次重启zabbix-agent2 1&#xff0c;用systemctl status zabbix-agent2查看报错…
阅读更多...
【漏洞复现】Atlassian Confluence RCE(CVE-2023-22527)

【漏洞复现】Atlassian Confluence RCE(CVE-2023-22527)

产品简介 Atlassian Confluence 是一款由Atlassian开发的企业团队协作和知识管理软件&#xff0c;提供了一个集中化的平台&#xff0c;用于创建、组织和共享团队的文档、知识库、项目计划和协作内容。是面向大型企业和组织的高可用性、可扩展性和高性能版本。 0x02 漏洞概述 …
阅读更多...
综合布线实训室建设可行性报告

综合布线实训室建设可行性报告

1、 建设综合布线实训室的目的和意义 1.1 响应国家职业教育政策 在国家对职业教育的高度重视和政策支持下&#xff0c;综合布线实训室的建设不仅是对国家教育方针的积极响应&#xff0c;也是对技术教育改革的有力推动。通过这一平台&#xff0c;我们旨在培育出一批具有强烈实…
阅读更多...
全面体验ONLYOFFICE 8.1版本桌面编辑器

全面体验ONLYOFFICE 8.1版本桌面编辑器

ONLYOFFICE官网 在当今的数字化办公环境中&#xff0c;选择合适的文档处理工具对于提升工作效率和团队协作至关重要。ONLYOFFICE 8.1版本桌面编辑器&#xff0c;作为一款集成了多项先进功能的办公软件&#xff0c;为用户提供了全新的办公体验。今天&#xff0c;我们将深入探索…
阅读更多...
[linux]sed命令基础入门详解

[linux]sed命令基础入门详解

sed是一种流编辑器&#xff0c;它一次处理一行内容。处理时&#xff0c;把当前处理的行存储在临时缓冲区中&#xff0c;称为“模式空间”&#xff0c;接着用sed命令处理缓冲区中的内容&#xff0c;处理完成后&#xff0c;把缓冲区的内容送往屏幕。接着处理下一行&#xff0c;这…
阅读更多...
imx6ull/linux应用编程学习(5）FrameBuffer的应用编程

imx6ull/linux应用编程学习(5）FrameBuffer的应用编程

什么是FrameBuffer&#xff1f; Frame 是帧的意思&#xff0c; buffer 是缓冲的意思&#xff0c;所以 Framebuffer 就是帧缓冲&#xff0c; 这意味着 Framebuffer 就是一块内存&#xff0c;里面保存着一帧图像。帧缓冲&#xff08;framebuffer&#xff09;是 Linux 系统中的一种…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023