多年来,我一直在使用 PyTorch 构建和训练深度学习模型。尽管我已经学会了它的语法和规则,但总有一些东西激起了我的好奇心:这些操作内部发生了什么?这一切是如何运作的?
如果你已经到这里,你可能也有同样的问题。如果我问你如何在 PyTorch 中创建和训练模型,你可能会想出类似下面的代码:
import torch
import torch.nn as nn
import torch.optim as optim
class MyModel(nn.Module):
def __init__(self):
super(MyModel, self).__init__()
self.fc1 = nn.Linear(1, 10)
self.sigmoid = nn.Sigmoid()
self.fc2 = nn.Linear(10, 1)
def forward(self, x):
out = self.fc1(x)
out = self.sigmoid(out)
out = self.fc2(out)
return out
...
model = MyModel().to(device)
criterion = nn.MSELoss()
optimizer = optim.SGD(model.parameters(), lr=0.001)
for epoch in range(epochs):
for x, y in ...
x = x.to(device)
y = y.to(device)
outputs = model(x)
loss = criterion(outputs, y)
optimizer.zero_grad()
loss.backward()
optimizer.step()但是如果我问你这个后退步骤是如何工作的呢?或者,例如,当你重塑张量时会发生什么?数据是否在内部重新排列?这是怎么发生的?为什么 PyTorch 这么快?PyTorch 如何处理 GPU 操作?这些类型的问题一直让我着迷,我想它们也让你着迷。因此,为了更好地理解这些概念,有什么比从头开始构建自己的张量库更好的呢?这就是你将在本文中学习的内容!

NSDT工具推荐: Three.js AI纹理开发包 - YOLO合成数据生成器 - GLTF/GLB在线编辑 - 3D模型格式在线转换 - 可编程3D场景编辑器 - REVIT导出3D模型插件 - 3D模型语义搜索引擎 - Three.js虚拟轴心开发包 - 3D模型在线减面 - STL模型在线切割
1、张量
为了构建张量库,你需要学习的第一个概念显然是:什么是张量?
你可能有一个直观的想法,张量是包含一些数字的 n 维数据结构的数学概念。但在这里我们需要了解如何从计算角度对这种数据结构进行建模。我们可以将张量视为由数据本身以及描述张量的各个方面(例如其形状或其所在的设备(即 CPU 内存、GPU 内存……))的一些元数据组成。

还有一个你可能从未听说过的不太流行的元数据,称为步幅(stride)。这个概念对于理解张量数据重排的内部原理非常重要,所以我们需要进一步讨论它。
想象一个形状为 [4, 8] 的二维张量,如下图所示:

4x8 Tensor
张量的数据实际上作为一维数组存储在内存中:
![]()
张量的一维数据数组
因此,为了将这个一维数组表示为 N 维张量,我们使用步长。基本思路如下:
我们有一个 4 行 8 列的矩阵。考虑到它的所有元素都是按一维数组上的行组织的,如果我们想要访问位置 [2, 3] 的值,我们需要遍历 2 行(每行 8 个元素)加上 3 个位置。用数学术语来说,我们需要遍历一维数组上的 3 + 2 * 8 个元素:

所以这个‘8’是第二维的步幅。在这种情况下,它是我需要在数组上遍历多少个元素才能“跳”到第二维上的其他位置的信息。
因此,为了访问形状为 [shape_0,shape_1]的二维张量的元素 [i,j],我们基本上需要访问位置 j + i * shape_1的元素
现在,让我们想象一个三维张量:
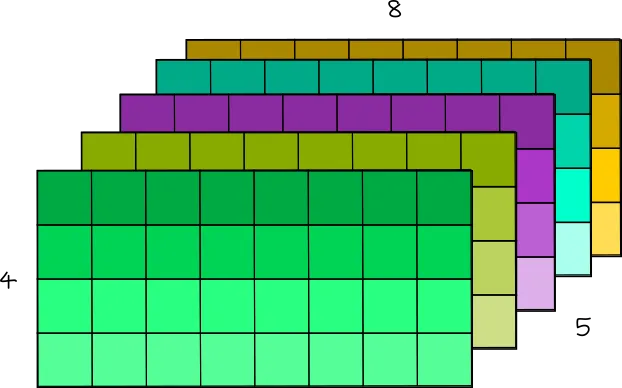
5x4x8 Tensor
你可以将这个三维张量视为矩阵序列。例如,可以将这个 [5, 4, 8] 张量视为 5 个形状为 [4, 8] 的矩阵。
现在,为了访问位置 [1, 2, 7] 处的元素,你需要遍历 1 个形状为 [4,8] 的完整矩阵、2 行形状为 [8] 的矩阵和 7 列形状为 [1] 的矩阵。因此,你需要遍历一维数组上的 (1 * 4 * 8) + (2 * 8) + (7 * 1) 个位置。

因此,要访问一维数据数组中具有 [shape_0, shape_1, shape_2] 的三维张量的元素 [i][j][k],可以执行以下操作:

这个 shape_1 * shape_2是第一维的步幅, shape_2是第二维的步幅,1是第三维的步幅。
然后,为了概括:
![]()
其中每个维度的步幅可以使用下一维张量形状的乘积来计算:

然后我们设置 stride[n-1] = 1。
在我们的形状为 [5, 4, 8] 的张量示例中,我们将有 strides = [4*8, 8, 1] = [32, 8, 1]
你可以自行测试:
import torch
torch.rand([5, 4, 8]).stride()
#(32, 8, 1)好的,但是为什么我们需要形状和步幅?除了访问存储为一维数组的 N 维张量的元素之外,这个概念还可用于非常轻松地操纵张量排列。
例如,要重塑张量,你只需设置新形状并根据它计算新步幅!(因为新形状保证了相同数量的元素):
import torch
t = torch.rand([5, 4, 8])
print(t.shape)
# [5, 4, 8]
print(t.stride())
# [32, 8, 1]
new_t = t.reshape([4, 5, 2, 2, 2])
print(new_t.shape)
# [4, 5, 2, 2, 2]
print(new_t.stride())
# [40, 8, 4, 2, 1]在内部,张量仍然存储为相同的一维数组。 reshape 方法没有改变数组内元素的顺序!这很神奇,不是吗?😁
你可以使用以下函数自行验证,该函数访问 PyTorch 上的内部一维数组:
import ctypes
def print_internal(t: torch.Tensor):
print(
torch.frombuffer(
ctypes.string_at(t.data_ptr(), t.storage().nbytes()), dtype=t.dtype
)
)
print_internal(t)
# [0.0752, 0.5898, 0.3930, 0.9577, 0.2276, 0.9786, 0.1009, 0.138, ...
print_internal(new_t)
# [0.0752, 0.5898, 0.3930, 0.9577, 0.2276, 0.9786, 0.1009, 0.138, ...例如,你想转置两个轴。在内部,你只需要交换相应的步幅!
t = torch.arange(0, 24).reshape(2, 3, 4)
print(t)
# [[[ 0, 1, 2, 3],
# [ 4, 5, 6, 7],
# [ 8, 9, 10, 11]],
# [[12, 13, 14, 15],
# [16, 17, 18, 19],
# [20, 21, 22, 23]]]
print(t.shape)
# [2, 3, 4]
print(t.stride())
# [12, 4, 1]
new_t = t.transpose(0, 1)
print(new_t)
# [[[ 0, 1, 2, 3],
# [12, 13, 14, 15]],
# [[ 4, 5, 6, 7],
# [16, 17, 18, 19]],
# [[ 8, 9, 10, 11],
# [20, 21, 22, 23]]]
print(new_t.shape)
# [3, 2, 4]
print(new_t.stride())
# [4, 12, 1]如果打印内部数组,两者都具有相同的值:
print_internal(t)
# [ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23]
print_internal(new_t)
# [ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23]但是, new_t 的步幅现在与我上面展示的方程不匹配。这是因为张量现在不连续。这意味着虽然内部数组保持不变,但其值在内存中的顺序与张量的实际顺序不匹配。
t.is_contiguous()
# True
new_t.is_contiguous()
# False这意味着按顺序访问不连续的元素效率较低(因为实数张量元素在内存中不是按顺序排列的)。为了解决这个问题,我们可以这样做:
new_t_contiguous = new_t.contiguous()
print(new_t_contiguous.is_contiguous())
# True如果我们分析内部数组,它的顺序现在与实际张量顺序相匹配,可以提供更好的内存访问效率:
print(new_t)
# [[[ 0, 1, 2, 3],
# [12, 13, 14, 15]],
# [[ 4, 5, 6, 7],
# [16, 17, 18, 19]],
# [[ 8, 9, 10, 11],
# [20, 21, 22, 23]]]
print_internal(new_t)
# [ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23]
print_internal(new_t_contiguous)
# [ 0, 1, 2, 3, 12, 13, 14, 15, 4, 5, 6, 7, 16, 17, 18, 19, 8, 9, 10, 11, 20, 21, 22, 23]现在我们理解了张量是如何建模的,让我们开始创建我们的库吧!
我将其命名为 Norch,它代表 NOT PyTorch,也暗指我的姓氏 Nogueira 😁
首先要知道的是,虽然 PyTorch 是通过 Python 使用的,但它内部运行的是 C/C++。因此,我们将首先创建内部 C/C++ 函数。
我们可以首先将张量定义为结构体来存储其数据和元数据,并创建一个函数来实例化它:
//norch/csrc/tensor.cpp
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <math.h>
typedef struct {
float* data;
int* strides;
int* shape;
int ndim;
int size;
char* device;
} Tensor;
Tensor* create_tensor(float* data, int* shape, int ndim) {
Tensor* tensor = (Tensor*)malloc(sizeof(Tensor));
if (tensor == NULL) {
fprintf(stderr, "Memory allocation failed\n");
exit(1);
}
tensor->data = data;
tensor->shape = shape;
tensor->ndim = ndim;
tensor->size = 1;
for (int i = 0; i < ndim; i++) {
tensor->size *= shape[i];
}
tensor->strides = (int*)malloc(ndim * sizeof(int));
if (tensor->strides == NULL) {
fprintf(stderr, "Memory allocation failed\n");
exit(1);
}
int stride = 1;
for (int i = ndim - 1; i >= 0; i--) {
tensor->strides[i] = stride;
stride *= shape[i];
}
return tensor;
}为了访问某些元素,我们可以利用步幅,正如我们之前所了解的:
//norch/csrc/tensor.cpp
float get_item(Tensor* tensor, int* indices) {
int index = 0;
for (int i = 0; i < tensor->ndim; i++) {
index += indices[i] * tensor->strides[i];
}
float result;
result = tensor->data[index];
return result;
}现在,我们可以创建张量运算了。我将展示一些示例,你可以在本文末尾链接的存储库中找到完整版本:
//norch/csrc/cpu.cpp
void add_tensor_cpu(Tensor* tensor1, Tensor* tensor2, float* result_data) {
for (int i = 0; i < tensor1->size; i++) {
result_data[i] = tensor1->data[i] + tensor2->data[i];
}
}
void sub_tensor_cpu(Tensor* tensor1, Tensor* tensor2, float* result_data) {
for (int i = 0; i < tensor1->size; i++) {
result_data[i] = tensor1->data[i] - tensor2->data[i];
}
}
void elementwise_mul_tensor_cpu(Tensor* tensor1, Tensor* tensor2, float* result_data) {
for (int i = 0; i < tensor1->size; i++) {
result_data[i] = tensor1->data[i] * tensor2->data[i];
}
}
void assign_tensor_cpu(Tensor* tensor, float* result_data) {
for (int i = 0; i < tensor->size; i++) {
result_data[i] = tensor->data[i];
}
}
...之后,我们能够创建其他张量函数来调用这些操作:
//norch/csrc/tensor.cpp
Tensor* add_tensor(Tensor* tensor1, Tensor* tensor2) {
if (tensor1->ndim != tensor2->ndim) {
fprintf(stderr, "Tensors must have the same number of dimensions %d and %d for addition\n", tensor1->ndim, tensor2->ndim);
exit(1);
}
int ndim = tensor1->ndim;
int* shape = (int*)malloc(ndim * sizeof(int));
if (shape == NULL) {
fprintf(stderr, "Memory allocation failed\n");
exit(1);
}
for (int i = 0; i < ndim; i++) {
if (tensor1->shape[i] != tensor2->shape[i]) {
fprintf(stderr, "Tensors must have the same shape %d and %d at index %d for addition\n", tensor1->shape[i], tensor2->shape[i], i);
exit(1);
}
shape[i] = tensor1->shape[i];
}
float* result_data = (float*)malloc(tensor1->size * sizeof(float));
if (result_data == NULL) {
fprintf(stderr, "Memory allocation failed\n");
exit(1);
}
add_tensor_cpu(tensor1, tensor2, result_data);
return create_tensor(result_data, shape, ndim, device);
}如前所述,张量重塑不会修改内部数据数组:
//norch/csrc/tensor.cpp
Tensor* reshape_tensor(Tensor* tensor, int* new_shape, int new_ndim) {
int ndim = new_ndim;
int* shape = (int*)malloc(ndim * sizeof(int));
if (shape == NULL) {
fprintf(stderr, "Memory allocation failed\n");
exit(1);
}
for (int i = 0; i < ndim; i++) {
shape[i] = new_shape[i];
}
// Calculate the total number of elements in the new shape
int size = 1;
for (int i = 0; i < new_ndim; i++) {
size *= shape[i];
}
// Check if the total number of elements matches the current tensor's size
if (size != tensor->size) {
fprintf(stderr, "Cannot reshape tensor. Total number of elements in new shape does not match the current size of the tensor.\n");
exit(1);
}
float* result_data = (float*)malloc(tensor->size * sizeof(float));
if (result_data == NULL) {
fprintf(stderr, "Memory allocation failed\n");
exit(1);
}
assign_tensor_cpu(tensor, result_data);
return create_tensor(result_data, shape, ndim, device);
}虽然我们现在可以进行一些张量运算,但没人值得使用 C/C++ 来运行它,对吧?让我们开始构建我们的 Python 包装器吧!
有很多使用 Python 运行 C/C++ 代码的选项,例如 Pybind11 和 Cython。对于我们的示例,我将使用 ctypes。
ctypes 的基本结构如下所示:
//C code
#include <stdio.h>
float add_floats(float a, float b) {
return a + b;
}# Compile
gcc -shared -o add_floats.so -fPIC add_floats.c# Python code
import ctypes
# Load the shared library
lib = ctypes.CDLL('./add_floats.so')
# Define the argument and return types for the function
lib.add_floats.argtypes = [ctypes.c_float, ctypes.c_float]
lib.add_floats.restype = ctypes.c_float
# Convert python float to c_float type
a = ctypes.c_float(3.5)
b = ctypes.c_float(2.2)
# Call the C function
result = lib.add_floats(a, b)
print(result)
# 5.7如你所见,它非常直观。编译 C/C++ 代码后,你可以非常轻松地在 Python 上使用 ctypes。只需定义函数的参数和返回 c_types,将变量转换为其各自的 c_types 并调用该函数。对于更复杂的类型(例如数组(浮点列表),可以使用指针:
data = [1.0, 2.0, 3.0]
data_ctype = (ctypes.c_float * len(data))(*data)
lib.some_array_func.argstypes = [ctypes.POINTER(ctypes.c_float)]
...
lib.some_array_func(data)对于结构类型,我们可以创建自己的 c_type:
class CustomType(ctypes.Structure):
_fields_ = [
('field1', ctypes.POINTER(ctypes.c_float)),
('field2', ctypes.POINTER(ctypes.c_int)),
('field3', ctypes.c_int),
]
# Can be used as ctypes.POINTER(CustomType)经过这个简短的解释之后,让我们为我们的张量 C/C++ 库构建 Python 包装器!
# norch/tensor.py
import ctypes
class CTensor(ctypes.Structure):
_fields_ = [
('data', ctypes.POINTER(ctypes.c_float)),
('strides', ctypes.POINTER(ctypes.c_int)),
('shape', ctypes.POINTER(ctypes.c_int)),
('ndim', ctypes.c_int),
('size', ctypes.c_int),
]
class Tensor:
os.path.abspath(os.curdir)
_C = ctypes.CDLL("COMPILED_LIB.so"))
def __init__(self):
data, shape = self.flatten(data)
self.data_ctype = (ctypes.c_float * len(data))(*data)
self.shape_ctype = (ctypes.c_int * len(shape))(*shape)
self.ndim_ctype = ctypes.c_int(len(shape))
self.shape = shape
self.ndim = len(shape)
Tensor._C.create_tensor.argtypes = [ctypes.POINTER(ctypes.c_float), ctypes.POINTER(ctypes.c_int), ctypes.c_int]
Tensor._C.create_tensor.restype = ctypes.POINTER(CTensor)
self.tensor = Tensor._C.create_tensor(
self.data_ctype,
self.shape_ctype,
self.ndim_ctype,
)
def flatten(self, nested_list):
"""
This method simply convert a list type tensor to a flatten tensor with its shape
Example:
Arguments:
nested_list: [[1, 2, 3], [-5, 2, 0]]
Return:
flat_data: [1, 2, 3, -5, 2, 0]
shape: [2, 3]
"""
def flatten_recursively(nested_list):
flat_data = []
shape = []
if isinstance(nested_list, list):
for sublist in nested_list:
inner_data, inner_shape = flatten_recursively(sublist)
flat_data.extend(inner_data)
shape.append(len(nested_list))
shape.extend(inner_shape)
else:
flat_data.append(nested_list)
return flat_data, shape
flat_data, shape = flatten_recursively(nested_list)
return flat_data, shape现在我们包含 Python 张量运算来调用 C/C++ 运算。
# norch/tensor.py
def __getitem__(self, indices):
"""
Access tensor by index tensor[i, j, k...]
"""
if len(indices) != self.ndim:
raise ValueError("Number of indices must match the number of dimensions")
Tensor._C.get_item.argtypes = [ctypes.POINTER(CTensor), ctypes.POINTER(ctypes.c_int)]
Tensor._C.get_item.restype = ctypes.c_float
indices = (ctypes.c_int * len(indices))(*indices)
value = Tensor._C.get_item(self.tensor, indices)
return value
def reshape(self, new_shape):
"""
Reshape tensor
result = tensor.reshape([1,2])
"""
new_shape_ctype = (ctypes.c_int * len(new_shape))(*new_shape)
new_ndim_ctype = ctypes.c_int(len(new_shape))
Tensor._C.reshape_tensor.argtypes = [ctypes.POINTER(CTensor), ctypes.POINTER(ctypes.c_int), ctypes.c_int]
Tensor._C.reshape_tensor.restype = ctypes.POINTER(CTensor)
result_tensor_ptr = Tensor._C.reshape_tensor(self.tensor, new_shape_ctype, new_ndim_ctype)
result_data = Tensor()
result_data.tensor = result_tensor_ptr
result_data.shape = new_shape.copy()
result_data.ndim = len(new_shape)
result_data.device = self.device
return result_data
def __add__(self, other):
"""
Add tensors
result = tensor1 + tensor2
"""
if self.shape != other.shape:
raise ValueError("Tensors must have the same shape for addition")
Tensor._C.add_tensor.argtypes = [ctypes.POINTER(CTensor), ctypes.POINTER(CTensor)]
Tensor._C.add_tensor.restype = ctypes.POINTER(CTensor)
result_tensor_ptr = Tensor._C.add_tensor(self.tensor, other.tensor)
result_data = Tensor()
result_data.tensor = result_tensor_ptr
result_data.shape = self.shape.copy()
result_data.ndim = self.ndim
result_data.device = self.device
return result_data
# Include the other operations:
# __str__
# __sub__ (-)
# __mul__ (*)
# __matmul__ (@)
# __pow__ (**)
# __truediv__ (/)
# log
# ...如果你到达这里,现在就可以运行代码并开始执行一些张量运算!
import norch
tensor1 = norch.Tensor([[1, 2, 3], [3, 2, 1]])
tensor2 = norch.Tensor([[3, 2, 1], [1, 2, 3]])
result = tensor1 + tensor2
print(result[0, 0])
# 4 2、GPU 支持
在创建了库的基本结构之后,我们现在将其提升到一个新的水平。众所周知,你可以调用 .to("cuda") 将数据发送到 GPU 并更快地运行数学运算。我假设你对 CUDA 的工作原理有基本的了解,但如果没有,你可以阅读我的另一篇文章CUDA 教程。
…
对于那些赶时间的人,这里做一个简单的介绍:
基本上,到目前为止,我们的所有代码都在 CPU 内存上运行。虽然对于单个操作来说 CPU 更快,但 GPU 的优势在于其并行化能力。虽然 CPU 设计旨在快速执行一系列操作(线程),但只能执行数十个,而 GPU 设计旨在并行执行数百万个操作(通过牺牲单个线程的性能)。
因此,我们可以利用此功能并行执行操作。例如,在百万级张量加法中,我们无需在循环内按顺序添加每个索引的元素,而是使用 GPU 一次性并行添加所有元素。为此,我们可以使用 CUDA,这是 NVIDIA 开发的一个平台,使开发人员能够将 GPU 支持集成到他们的软件应用程序中。
为此,你可以使用 CUDA C/C++,这是一个基于 C/C++ 的简单接口,旨在运行特定的 GPU 操作(例如将数据从 CPU 内存复制到 GPU 内存)。
下面的代码基本上使用一些 CUDA C/C++ 函数将数据从 CPU 复制到 GPU,并在总共 N 个 GPU 线程上并行运行 AddTwoArrays 函数(也称为内核),每个线程负责添加数组的不同元素:
#include <stdio.h>
// CPU version for comparison
void AddTwoArrays_CPU(flaot A[], float B[], float C[]) {
for (int i = 0; i < N; i++) {
C[i] = A[i] + B[i];
}
}
// Kernel definition
__global__ void AddTwoArrays_GPU(float A[], float B[], float C[]) {
int i = threadIdx.x;
C[i] = A[i] + B[i];
}
int main() {
int N = 1000; // Size of the arrays
float A[N], B[N], C[N]; // Arrays A, B, and C
...
float *d_A, *d_B, *d_C; // Device pointers for arrays A, B, and C
// Allocate memory on the device for arrays A, B, and C
cudaMalloc((void **)&d_A, N * sizeof(float));
cudaMalloc((void **)&d_B, N * sizeof(float));
cudaMalloc((void **)&d_C, N * sizeof(float));
// Copy arrays A and B from host to device
cudaMemcpy(d_A, A, N * sizeof(float), cudaMemcpyHostToDevice);
cudaMemcpy(d_B, B, N * sizeof(float), cudaMemcpyHostToDevice);
// Kernel invocation with N threads
AddTwoArrays_GPU<<<1, N>>>(d_A, d_B, d_C);
// Copy vector C from device to host
cudaMemcpy(C, d_C, N * sizeof(float), cudaMemcpyDeviceToHost);
}你可以注意到,我们不是每次操作都添加每个元素对,而是并行运行所有添加操作,从而摆脱了循环指令。
经过这个简短的介绍,我们可以回到我们的张量库。
第一步是创建一个函数,将张量数据从 CPU 发送到 GPU,反之亦然:
//norch/csrc/tensor.cpp
void to_device(Tensor* tensor, char* target_device) {
if ((strcmp(target_device, "cuda") == 0) && (strcmp(tensor->device, "cpu") == 0)) {
cpu_to_cuda(tensor);
}
else if ((strcmp(target_device, "cpu") == 0) && (strcmp(tensor->device, "cuda") == 0)) {
cuda_to_cpu(tensor);
}
}//norch/csrc/cuda.cu
__host__ void cpu_to_cuda(Tensor* tensor) {
float* data_tmp;
cudaMalloc((void **)&data_tmp, tensor->size * sizeof(float));
cudaMemcpy(data_tmp, tensor->data, tensor->size * sizeof(float), cudaMemcpyHostToDevice);
tensor->data = data_tmp;
const char* device_str = "cuda";
tensor->device = (char*)malloc(strlen(device_str) + 1);
strcpy(tensor->device, device_str);
printf("Successfully sent tensor to: %s\n", tensor->device);
}
__host__ void cuda_to_cpu(Tensor* tensor) {
float* data_tmp = (float*)malloc(tensor->size * sizeof(float));
cudaMemcpy(data_tmp, tensor->data, tensor->size * sizeof(float), cudaMemcpyDeviceToHost);
cudaFree(tensor->data);
tensor->data = data_tmp;
const char* device_str = "cpu";
tensor->device = (char*)malloc(strlen(device_str) + 1);
strcpy(tensor->device, device_str);
printf("Successfully sent tensor to: %s\n", tensor->device);
}Python 包装器:
# norch/tensor.py
def to(self, device):
self.device = device
self.device_ctype = self.device.encode('utf-8')
Tensor._C.to_device.argtypes = [ctypes.POINTER(CTensor), ctypes.c_char_p]
Tensor._C.to_device.restype = None
Tensor._C.to_device(self.tensor, self.device_ctype)
return self然后,我们为所有张量操作创建 GPU 版本。我将编写加法和减法的示例:
//norch/csrc/cuda.cu
#define THREADS_PER_BLOCK 128
__global__ void add_tensor_cuda_kernel(float* data1, float* data2, float* result_data, int size) {
int i = blockIdx.x * blockDim.x + threadIdx.x;
if (i < size) {
result_data[i] = data1[i] + data2[i];
}
}
__host__ void add_tensor_cuda(Tensor* tensor1, Tensor* tensor2, float* result_data) {
int number_of_blocks = (tensor1->size + THREADS_PER_BLOCK - 1) / THREADS_PER_BLOCK;
add_tensor_cuda_kernel<<<number_of_blocks, THREADS_PER_BLOCK>>>(tensor1->data, tensor2->data, result_data, tensor1->size);
cudaError_t error = cudaGetLastError();
if (error != cudaSuccess) {
printf("CUDA error: %s\n", cudaGetErrorString(error));
exit(-1);
}
cudaDeviceSynchronize();
}
__global__ void sub_tensor_cuda_kernel(float* data1, float* data2, float* result_data, int size) {
int i = blockIdx.x * blockDim.x + threadIdx.x;
if (i < size) {
result_data[i] = data1[i] - data2[i];
}
}
__host__ void sub_tensor_cuda(Tensor* tensor1, Tensor* tensor2, float* result_data) {
int number_of_blocks = (tensor1->size + THREADS_PER_BLOCK - 1) / THREADS_PER_BLOCK;
sub_tensor_cuda_kernel<<<number_of_blocks, THREADS_PER_BLOCK>>>(tensor1->data, tensor2->data, result_data, tensor1->size);
cudaError_t error = cudaGetLastError();
if (error != cudaSuccess) {
printf("CUDA error: %s\n", cudaGetErrorString(error));
exit(-1);
}
cudaDeviceSynchronize();
}
...随后,我们在 tensor.cpp 中包含一个新的张量属性 char* 设备,我们可以使用它来选择操作的运行位置(CPU 或 GPU):
//norch/csrc/tensor.cpp
Tensor* add_tensor(Tensor* tensor1, Tensor* tensor2) {
if (tensor1->ndim != tensor2->ndim) {
fprintf(stderr, "Tensors must have the same number of dimensions %d and %d for addition\n", tensor1->ndim, tensor2->ndim);
exit(1);
}
if (strcmp(tensor1->device, tensor2->device) != 0) {
fprintf(stderr, "Tensors must be on the same device: %s and %s\n", tensor1->device, tensor2->device);
exit(1);
}
char* device = (char*)malloc(strlen(tensor1->device) + 1);
if (device != NULL) {
strcpy(device, tensor1->device);
} else {
fprintf(stderr, "Memory allocation failed\n");
exit(-1);
}
int ndim = tensor1->ndim;
int* shape = (int*)malloc(ndim * sizeof(int));
if (shape == NULL) {
fprintf(stderr, "Memory allocation failed\n");
exit(1);
}
for (int i = 0; i < ndim; i++) {
if (tensor1->shape[i] != tensor2->shape[i]) {
fprintf(stderr, "Tensors must have the same shape %d and %d at index %d for addition\n", tensor1->shape[i], tensor2->shape[i], i);
exit(1);
}
shape[i] = tensor1->shape[i];
}
if (strcmp(tensor1->device, "cuda") == 0) {
float* result_data;
cudaMalloc((void **)&result_data, tensor1->size * sizeof(float));
add_tensor_cuda(tensor1, tensor2, result_data);
return create_tensor(result_data, shape, ndim, device);
}
else {
float* result_data = (float*)malloc(tensor1->size * sizeof(float));
if (result_data == NULL) {
fprintf(stderr, "Memory allocation failed\n");
exit(1);
}
add_tensor_cpu(tensor1, tensor2, result_data);
return create_tensor(result_data, shape, ndim, device);
}
}现在我们的库有 GPU 支持了!
import norch
tensor1 = norch.Tensor([[1, 2, 3], [3, 2, 1]]).to("cuda")
tensor2 = norch.Tensor([[3, 2, 1], [1, 2, 3]]).to("cuda")
result = tensor1 + tensor23、自动微分 (Autograd)
PyTorch 如此受欢迎的主要原因之一是它的 Autograd 模块。它是一个核心组件,允许自动微分以计算梯度(对于使用梯度下降等优化算法训练模型至关重要)。通过调用单个方法 .backward(),它可以计算来自先前张量操作的所有梯度:
x = torch.tensor([[1., 2, 3], [3., 2, 1]], requires_grad=True)
# [[1, 2, 3],
# [3, 2., 1]]
y = torch.tensor([[3., 2, 1], [1., 2, 3]], requires_grad=True)
# [[3, 2, 1],
# [1, 2, 3]]
L = ((x - y) ** 3).sum()
L.backward()
# You can access gradients of x and y
print(x.grad)
# [[12, 0, 12],
# [12, 0, 12]]
print(y.grad)
# [[-12, 0, -12],
# [-12, 0, -12]]
# In order to minimize z, you can use that for gradient descent:
# x = x - learning_rate * x.grad
# y = y - learning_rate * y.grad为了了解发生了什么,让我们尝试手动复制相同的过程:

我们先来计算一下:

请注意,x 是一个矩阵,因此我们需要分别计算 L 对每个元素的导数。此外,L 是所有元素的总和,但重要的是要记住,对于每个元素,其他元素不会干扰其导数。因此,我们得到以下项:

通过对每个项应用链式法则,我们区分外部函数并乘以内部函数的导数:
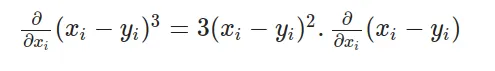
其中:

最后:

因此,我们有以下最终方程来计算 L 关于 x 的导数:

将数值代入方程式:

计算结果,我们得到与使用 PyTorch 获得的相同的值:

现在,让我们分析一下我们刚才所做的:
基本上,我们观察到了所有涉及保留顺序的运算:求和、3 的幂和减法。然后,我们应用规则链,计算每个运算的导数,并递归计算下一个运算的导数。因此,首先我们需要实现不同数学运算的导数:
对于加法:

# norch/autograd/functions.py
class AddBackward:
def __init__(self, x, y):
self.input = [x, y]
def backward(self, gradient):
return [gradient, gradient]对于sin:

# norch/autograd/functions.py
class SinBackward:
def __init__(self, x):
self.input = [x]
def backward(self, gradient):
x = self.input[0]
return [x.cos() * gradient]对于cosine:

# norch/autograd/functions.py
class CosBackward:
def __init__(self, x):
self.input = [x]
def backward(self, gradient):
x = self.input[0]
return [- x.sin() * gradient]对于元素乘法:

# norch/autograd/functions.py
class ElementwiseMulBackward:
def __init__(self, x, y):
self.input = [x, y]
def backward(self, gradient):
x = self.input[0]
y = self.input[1]
return [y * gradient, x * gradient]对于求和:
# norch/autograd/functions.py
class SumBackward:
def __init__(self, x):
self.input = [x]
def backward(self, gradient):
# Since sum reduces a tensor to a scalar, gradient is broadcasted to match the original shape.
return [float(gradient.tensor.contents.data[0]) * self.input[0].ones_like()]你可以访问文章末尾的 GitHub 存储库链接来探索其他操作。
现在我们有了每个操作的导数表达式,我们可以继续实现递归后向链式法则。我们可以为张量设置一个 require_grad 参数,以表明我们想要存储该张量的梯度。如果为真,我们将存储每个张量操作的梯度。例如:
# norch/tensor.py
def __add__(self, other):
if self.shape != other.shape:
raise ValueError("Tensors must have the same shape for addition")
Tensor._C.add_tensor.argtypes = [ctypes.POINTER(CTensor), ctypes.POINTER(CTensor)]
Tensor._C.add_tensor.restype = ctypes.POINTER(CTensor)
result_tensor_ptr = Tensor._C.add_tensor(self.tensor, other.tensor)
result_data = Tensor()
result_data.tensor = result_tensor_ptr
result_data.shape = self.shape.copy()
result_data.ndim = self.ndim
result_data.device = self.device
result_data.requires_grad = self.requires_grad or other.requires_grad
if result_data.requires_grad:
result_data.grad_fn = AddBackward(self, other)然后,实现 .backward()方法:
# norch/tensor.py
def backward(self, gradient=None):
if not self.requires_grad:
return
if gradient is None:
if self.shape == [1]:
gradient = Tensor([1]) # dx/dx = 1 case
else:
raise RuntimeError("Gradient argument must be specified for non-scalar tensors.")
if self.grad is None:
self.grad = gradient
else:
self.grad += gradient
if self.grad_fn is not None: # not a leaf
grads = self.grad_fn.backward(gradient) # call the operation backward
for tensor, grad in zip(self.grad_fn.input, grads):
if isinstance(tensor, Tensor):
tensor.backward(grad) # recursively call the backward again for the gradient expression (chain rule)最后,只需实现 .zero_grad() 将张量的梯度归零,并实现 .detach() 删除张量自动求导历史记录:
# norch/tensor.py
def zero_grad(self):
self.grad = None
def detach(self):
self.grad = None
self.grad_fn = None恭喜!您刚刚创建了一个具有 GPU 支持和自动微分的完整张量库!现在我们可以创建 nn 和 optim 模块来更轻松地训练一些深度学习模型。
4、nn 和 optim 模块
nn 是一个用于构建神经网络和深度学习模型的模块,optim 与用于训练这些模型的优化算法相关。为了重新创建它们,要做的第一件事是实现一个参数,它只是一个可训练的张量,具有相同的操作,但将 require_grad 始终设置为 True 并使用一些随机初始化技术。
# norch/nn/parameter.py
from norch.tensor import Tensor
from norch.utils import utils
import random
class Parameter(Tensor):
"""
A parameter is a trainable tensor.
"""
def __init__(self, shape):
data = utils.generate_random_list(shape=shape)
super().__init__(data, requires_grad=True)# norch/utisl/utils.py
def generate_random_list(shape):
"""
Generate a list with random numbers and shape 'shape'
[4, 2] --> [[rand1, rand2], [rand3, rand4], [rand5, rand6], [rand7, rand8]]
"""
if len(shape) == 0:
return []
else:
inner_shape = shape[1:]
if len(inner_shape) == 0:
return [random.uniform(-1, 1) for _ in range(shape[0])]
else:
return [generate_random_list(inner_shape) for _ in range(shape[0])]通过使用参数,我们可以开始构建模块:
# norch/nn/module.py
from .parameter import Parameter
from collections import OrderedDict
from abc import ABC
import inspect
class Module(ABC):
"""
Abstract class for modules
"""
def __init__(self):
self._modules = OrderedDict()
self._params = OrderedDict()
self._grads = OrderedDict()
self.training = True
def forward(self, *inputs, **kwargs):
raise NotImplementedError
def __call__(self, *inputs, **kwargs):
return self.forward(*inputs, **kwargs)
def train(self):
self.training = True
for param in self.parameters():
param.requires_grad = True
def eval(self):
self.training = False
for param in self.parameters():
param.requires_grad = False
def parameters(self):
for name, value in inspect.getmembers(self):
if isinstance(value, Parameter):
yield self, name, value
elif isinstance(value, Module):
yield from value.parameters()
def modules(self):
yield from self._modules.values()
def gradients(self):
for module in self.modules():
yield module._grads
def zero_grad(self):
for _, _, parameter in self.parameters():
parameter.zero_grad()
def to(self, device):
for _, _, parameter in self.parameters():
parameter.to(device)
return self
def inner_repr(self):
return ""
def __repr__(self):
string = f"{self.get_name()}("
tab = " "
modules = self._modules
if modules == {}:
string += f'\n{tab}(parameters): {self.inner_repr()}'
else:
for key, module in modules.items():
string += f"\n{tab}({key}): {module.get_name()}({module.inner_repr()})"
return f'{string}\n)'
def get_name(self):
return self.__class__.__name__
def __setattr__(self, key, value):
self.__dict__[key] = value
if isinstance(value, Module):
self._modules[key] = value
elif isinstance(value, Parameter):
self._params[key] = value例如,我们可以通过继承 nn.Module 来构建我们的自定义模块,或者我们可以使用一些以前创建的模块,例如实现 y = Wx + b 操作的线性模块。
# norch/nn/modules/linear.py
from ..module import Module
from ..parameter import Parameter
class Linear(Module):
def __init__(self, input_dim, output_dim):
super().__init__()
self.input_dim = input_dim
self.output_dim = output_dim
self.weight = Parameter(shape=[self.output_dim, self.input_dim])
self.bias = Parameter(shape=[self.output_dim, 1])
def forward(self, x):
z = self.weight @ x + self.bias
return z
def inner_repr(self):
return f"input_dim={self.input_dim}, output_dim={self.output_dim}, " \
f"bias={True if self.bias is not None else False}"现在我们可以实现一些损失和激活函数。例如,均方误差损失和 S 型函数:
# norch/nn/loss.py
from .module import Module
class MSELoss(Module):
def __init__(self):
pass
def forward(self, predictions, labels):
assert labels.shape == predictions.shape, \
"Labels and predictions shape does not match: {} and {}".format(labels.shape, predictions.shape)
return ((predictions - labels) ** 2).sum() / predictions.numel
def __call__(self, *inputs):
return self.forward(*inputs)# norch/nn/activation.py
from .module import Module
import math
class Sigmoid(Module):
def __init__(self):
super().__init__()
def forward(self, x):
return 1.0 / (1.0 + (math.e) ** (-x)) 最后,创建优化器。在我们的示例中,我将实现随机梯度下降算法:
# norch/optim/optimizer.py
from abc import ABC
from norch.tensor import Tensor
class Optimizer(ABC):
"""
Abstract class for optimizers
"""
def __init__(self, parameters):
if isinstance(parameters, Tensor):
raise TypeError("parameters should be an iterable but got {}".format(type(parameters)))
elif isinstance(parameters, dict):
parameters = parameters.values()
self.parameters = list(parameters)
def step(self):
raise NotImplementedError
def zero_grad(self):
for module, name, parameter in self.parameters:
parameter.zero_grad()
class SGD(Optimizer):
def __init__(self, parameters, lr=1e-1, momentum=0):
super().__init__(parameters)
self.lr = lr
self.momentum = momentum
self._cache = {'velocity': [p.zeros_like() for (_, _, p) in self.parameters]}
def step(self):
for i, (module, name, _) in enumerate(self.parameters):
parameter = getattr(module, name)
velocity = self._cache['velocity'][i]
velocity = self.momentum * velocity - self.lr * parameter.grad
updated_parameter = parameter + velocity
setattr(module, name, updated_parameter)
self._cache['velocity'][i] = velocity
parameter.detach()
velocity.detach()就这样!我们刚刚创建了自己的深度学习框架!🥳
让我们进行一些训练:
import norch
import norch.nn as nn
import norch.optim as optim
import random
import math
random.seed(1)
class MyModel(nn.Module):
def __init__(self):
super(MyModel, self).__init__()
self.fc1 = nn.Linear(1, 10)
self.sigmoid = nn.Sigmoid()
self.fc2 = nn.Linear(10, 1)
def forward(self, x):
out = self.fc1(x)
out = self.sigmoid(out)
out = self.fc2(out)
return out
device = "cuda"
epochs = 10
model = MyModel().to(device)
criterion = nn.MSELoss()
optimizer = optim.SGD(model.parameters(), lr=0.001)
loss_list = []
x_values = [0. , 0.4, 0.8, 1.2, 1.6, 2. , 2.4, 2.8, 3.2, 3.6, 4. ,
4.4, 4.8, 5.2, 5.6, 6. , 6.4, 6.8, 7.2, 7.6, 8. , 8.4,
8.8, 9.2, 9.6, 10. , 10.4, 10.8, 11.2, 11.6, 12. , 12.4, 12.8,
13.2, 13.6, 14. , 14.4, 14.8, 15.2, 15.6, 16. , 16.4, 16.8, 17.2,
17.6, 18. , 18.4, 18.8, 19.2, 19.6, 20.]
y_true = []
for x in x_values:
y_true.append(math.pow(math.sin(x), 2))
for epoch in range(epochs):
for x, target in zip(x_values, y_true):
x = norch.Tensor([[x]]).T
target = norch.Tensor([[target]]).T
x = x.to(device)
target = target.to(device)
outputs = model(x)
loss = criterion(outputs, target)
optimizer.zero_grad()
loss.backward()
optimizer.step()
print(f'Epoch [{epoch + 1}/{epochs}], Loss: {loss[0]:.4f}')
loss_list.append(loss[0])
# Epoch [1/10], Loss: 1.7035
# Epoch [2/10], Loss: 0.7193
# Epoch [3/10], Loss: 0.3068
# Epoch [4/10], Loss: 0.1742
# Epoch [5/10], Loss: 0.1342
# Epoch [6/10], Loss: 0.1232
# Epoch [7/10], Loss: 0.1220
# Epoch [8/10], Loss: 0.1241
# Epoch [9/10], Loss: 0.1270
# Epoch [10/10], Loss: 0.1297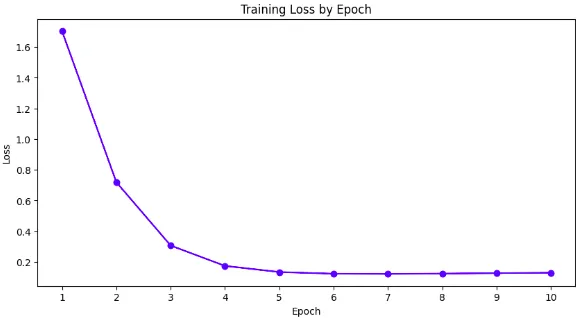
使用我们自定义的深度学习框架成功创建并训练了模型!
你可以在此处查看完整代码。
5、结束语
在这篇文章中,我们介绍了什么是张量、如何建模以及更高级的主题(例如 CUDA 和 Autograd)的基本概念。 我们成功创建了一个具有 GPU 支持和自动微分的深度学习框架。 我希望这篇文章能帮助你简要了解 PyTorch 的底层工作原理。
原文链接:从零创建深度学习框架 - BimAnt




![[linux]sed命令基础入门详解](https://i-blog.csdnimg.cn/direct/eb773c12c6fa44a6b6c814f5924676a6.png)