今天，小雅兰的内容是函数的求导法则，上篇博客我们知道了导数的定义、导数的几何意义及可导与连续关系，这篇博客我们来仔细学习一下求导法则，下面，就让我们进入导数的世界吧
一、函数的和、差、积、商的求导法则
二、反函数的求导法则
三、复合函数的求导法则
一、函数的和、差、积、商的求导法则
事实上，这些求导法则我们在高中时期就已经学习过了，但只是记的这个结论，并不知道它到底是怎么来的，下面，我们来证明一下这几个求导法则
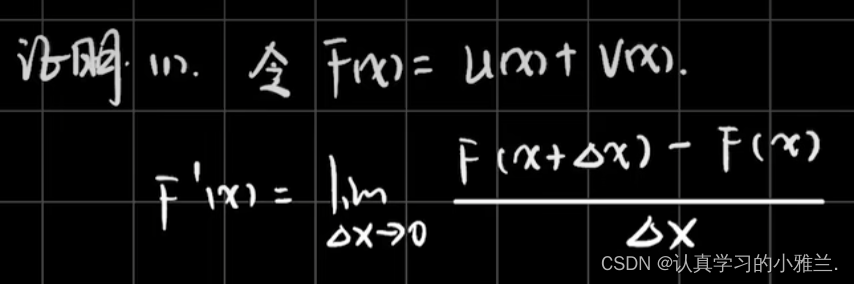
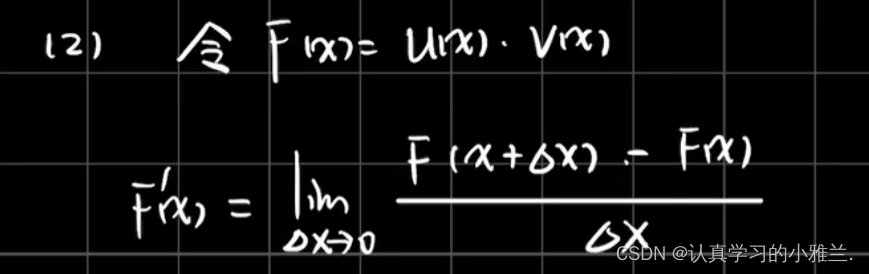
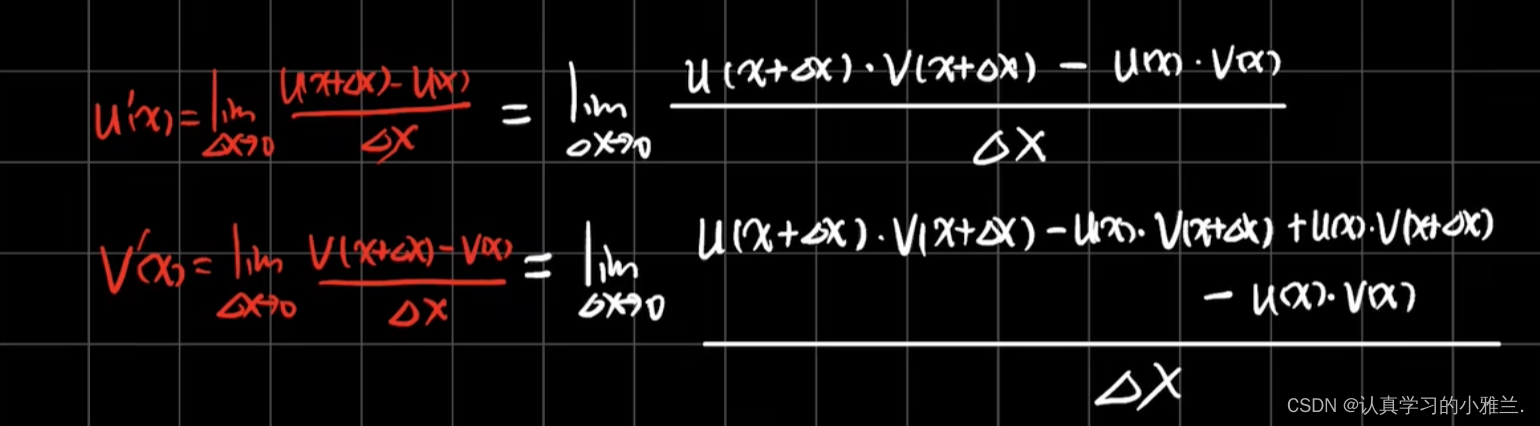
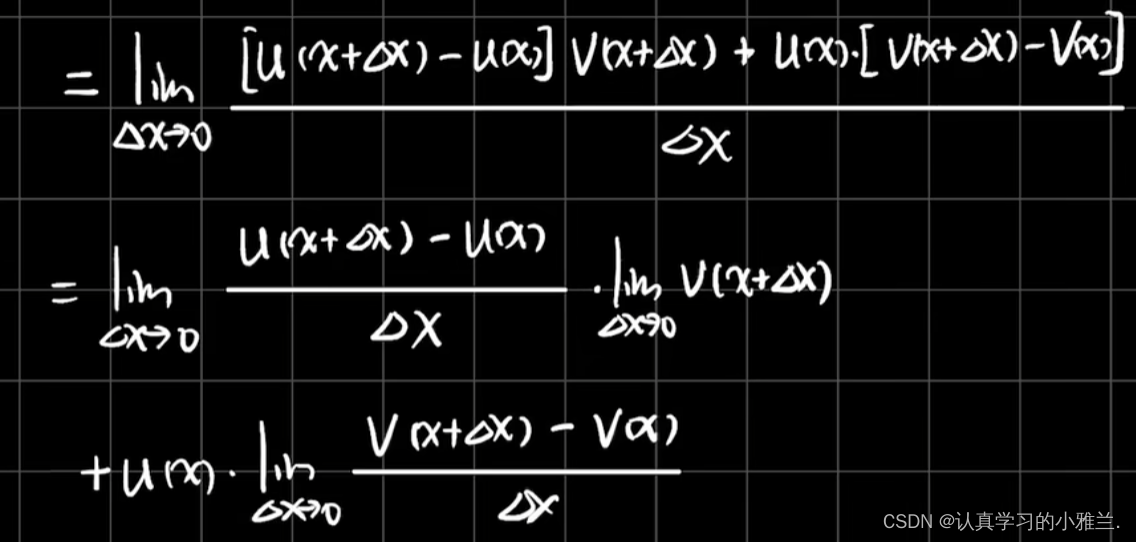
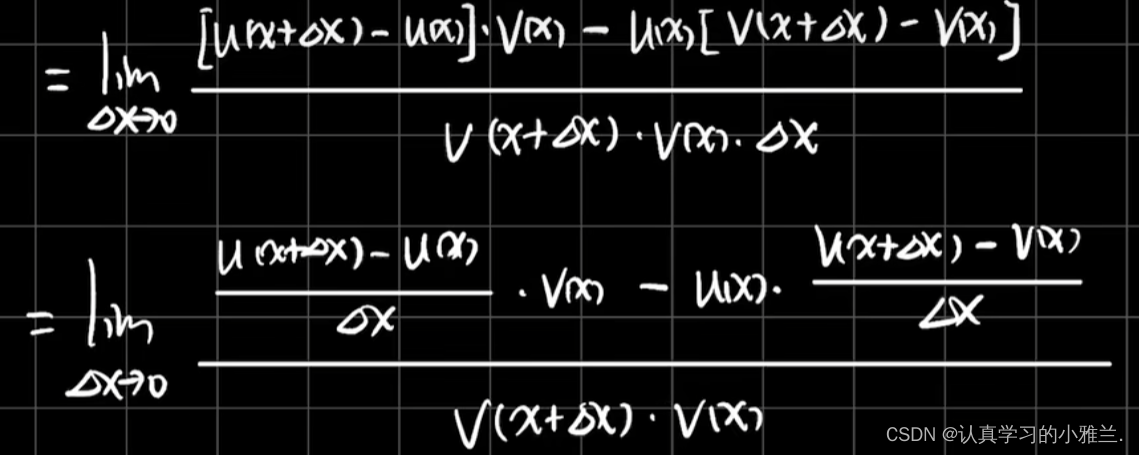
我们有个推广形式
下面，我们来看几个例题
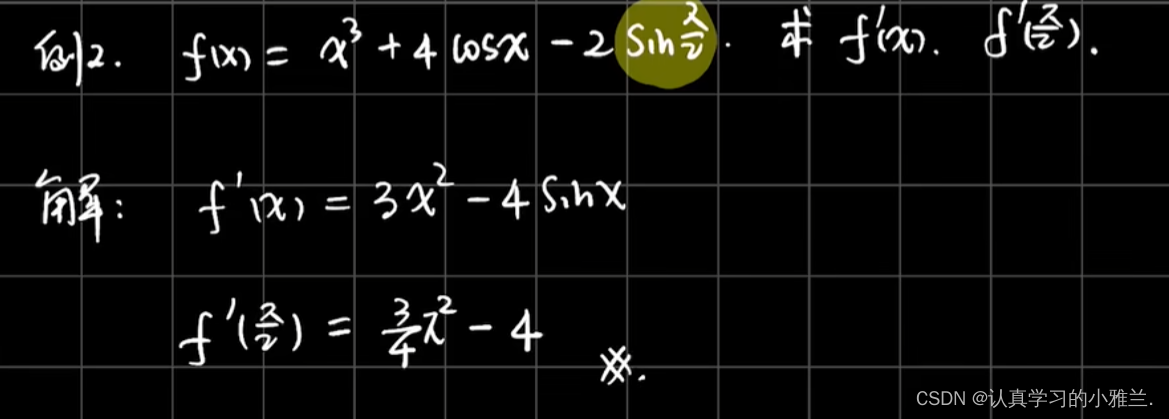这题要格外注意，sixpi/2为常数，常数求导为0
有很多人会犯这样的错误：sixpi/2求导得cospi/2
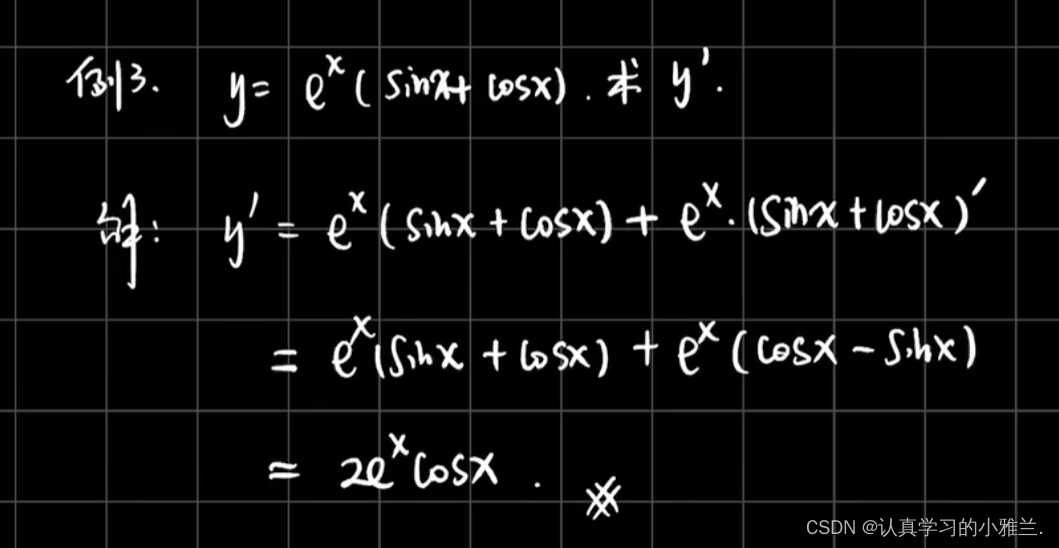
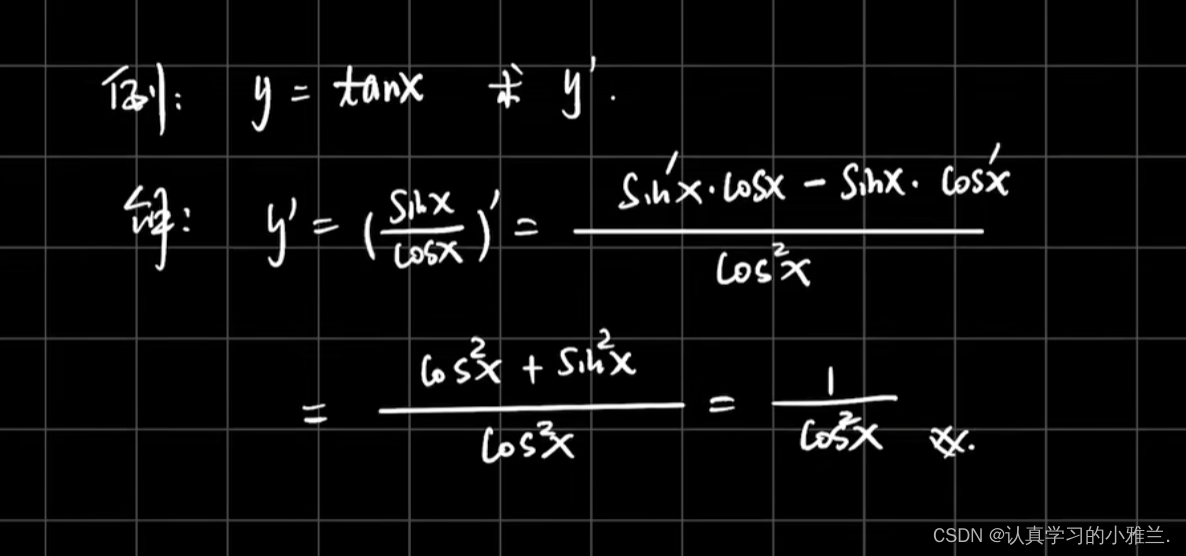
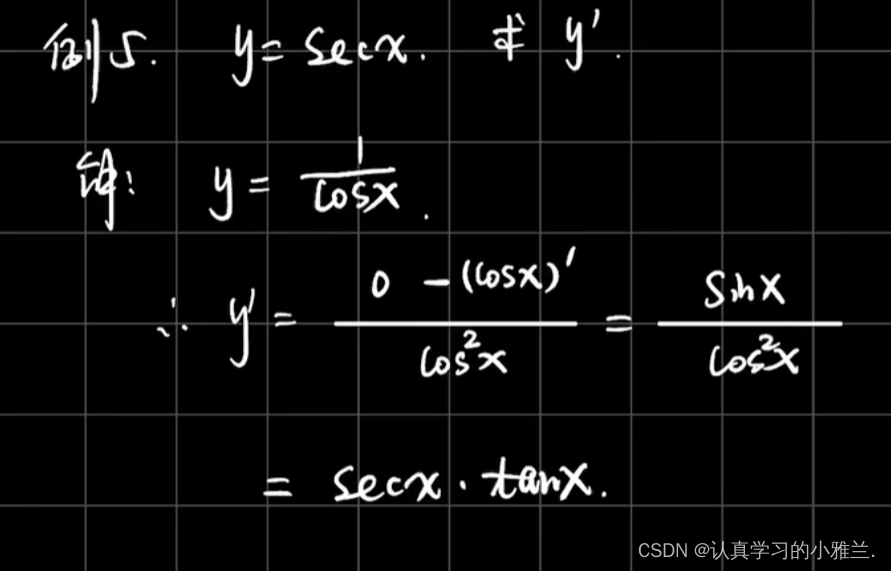
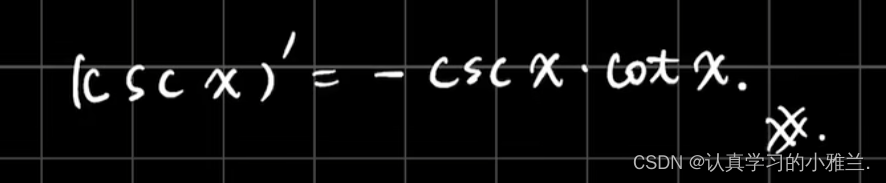
二、反函数的求导法则
下面，我们来证明一下此定理
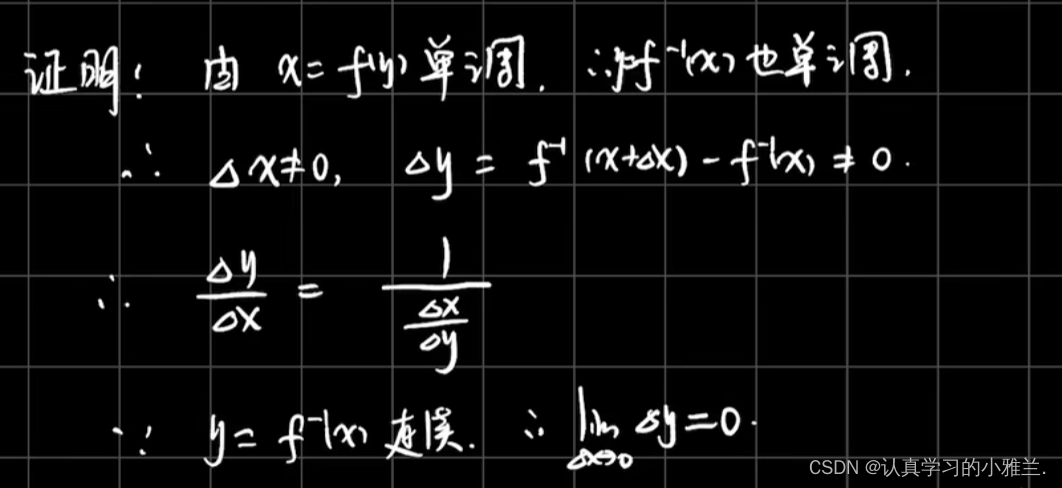
下面，我们来看几个例题
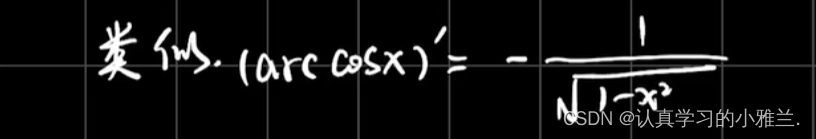
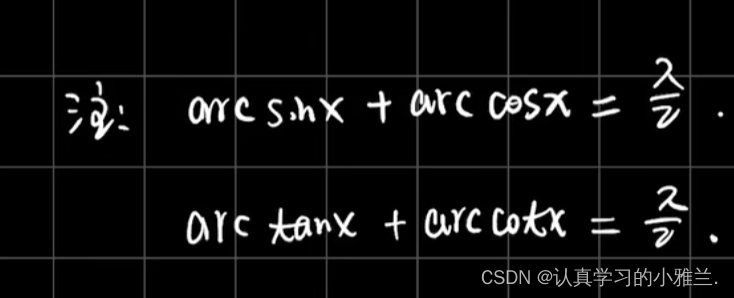
三、复合函数的求导法则
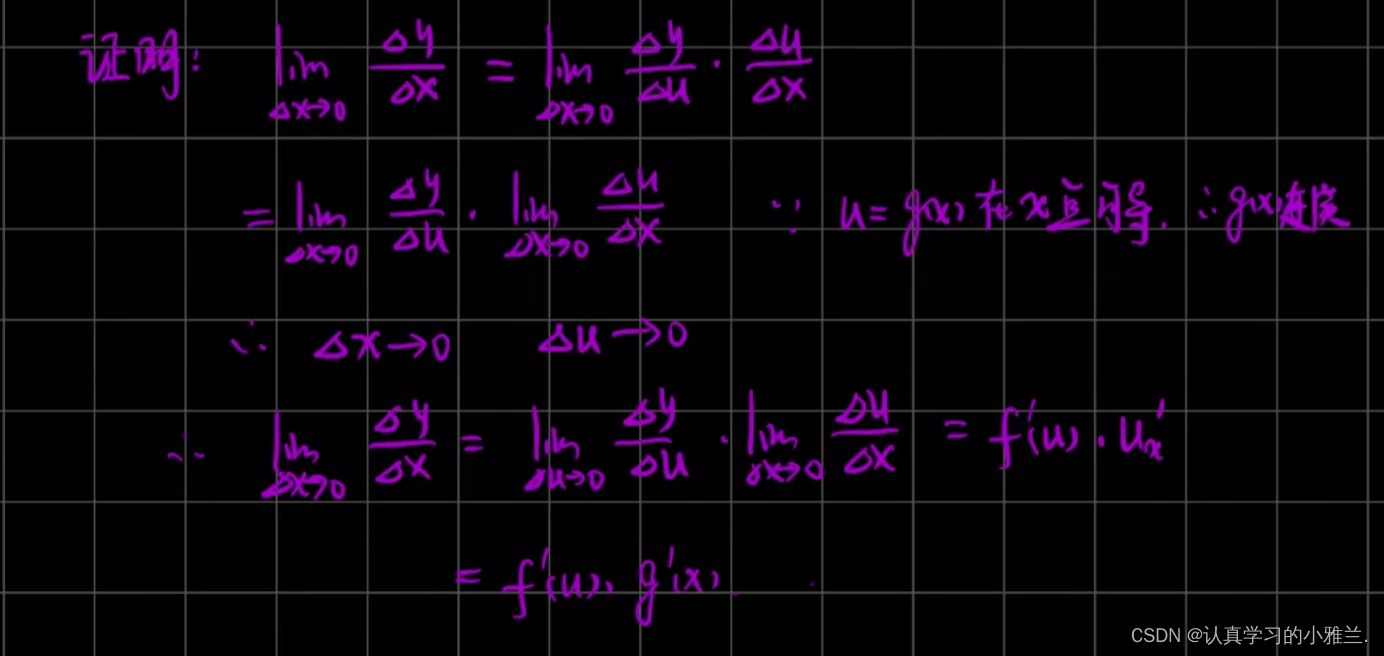但是这个证明过程是有缺陷的，因为采用的是除以一个（）u再乘以一个（）u的方式，这种方式要求（）u不能等于零，所以才有当（）x趋于零时，（）u也趋于零
虽然这种方式有缺陷，但是对于我们这种初学者来说，能够很好地理解就已经非常不错了
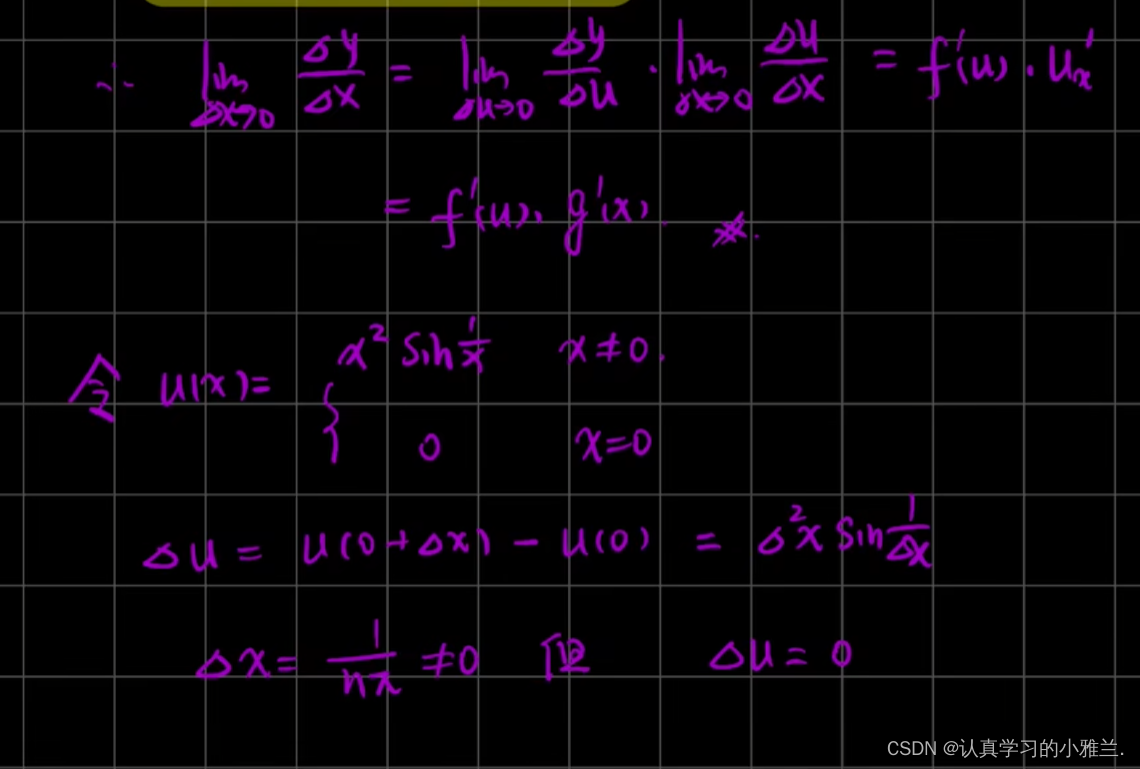下面，来给出严格的证明过程
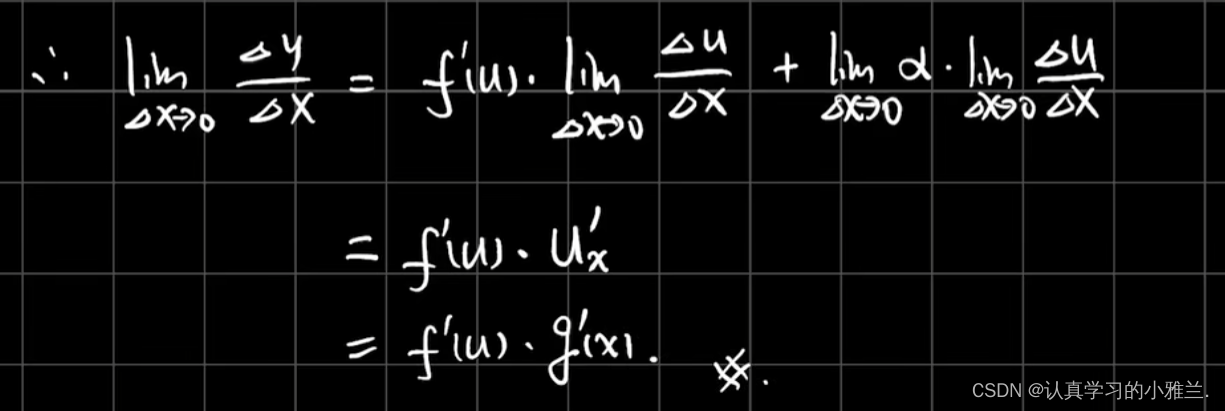
这个证明过程非常复杂，只需要做一个了解就可以了
下面，来看一下复合函数求导法则的推广形式
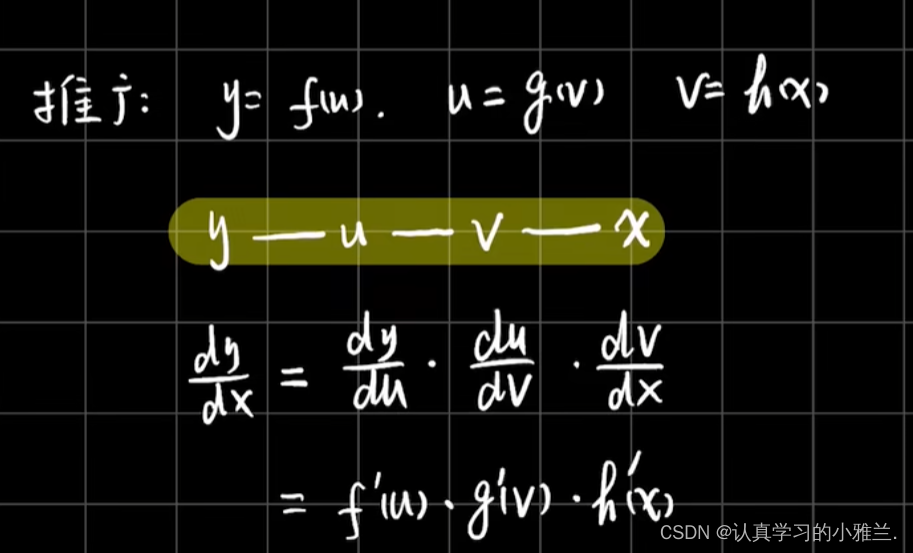
下面，我们来看几个例题
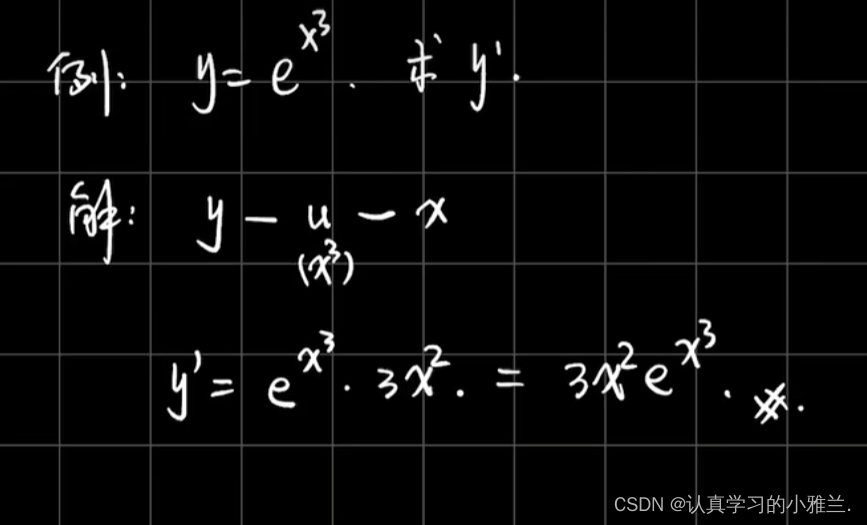
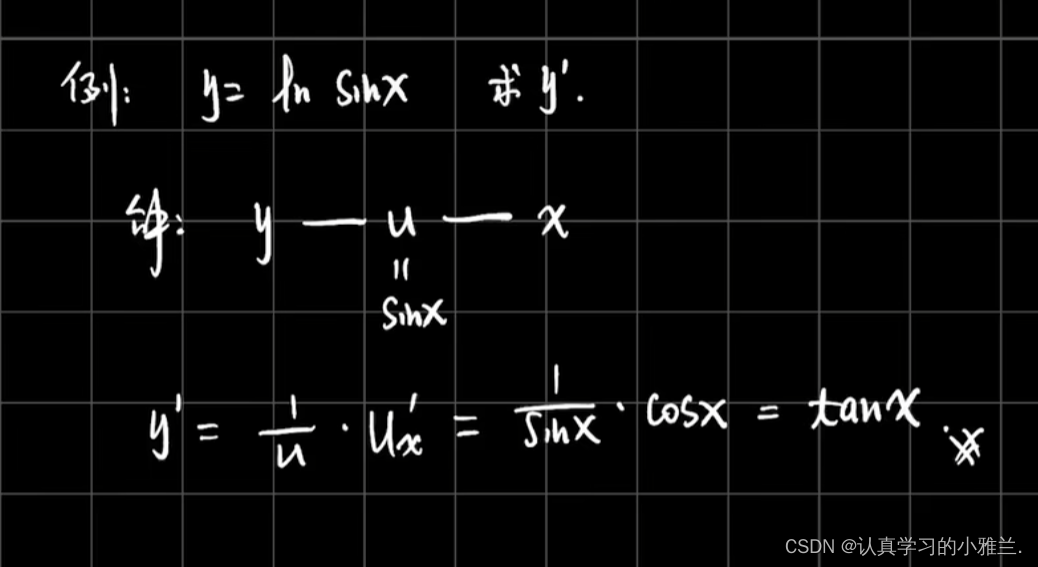
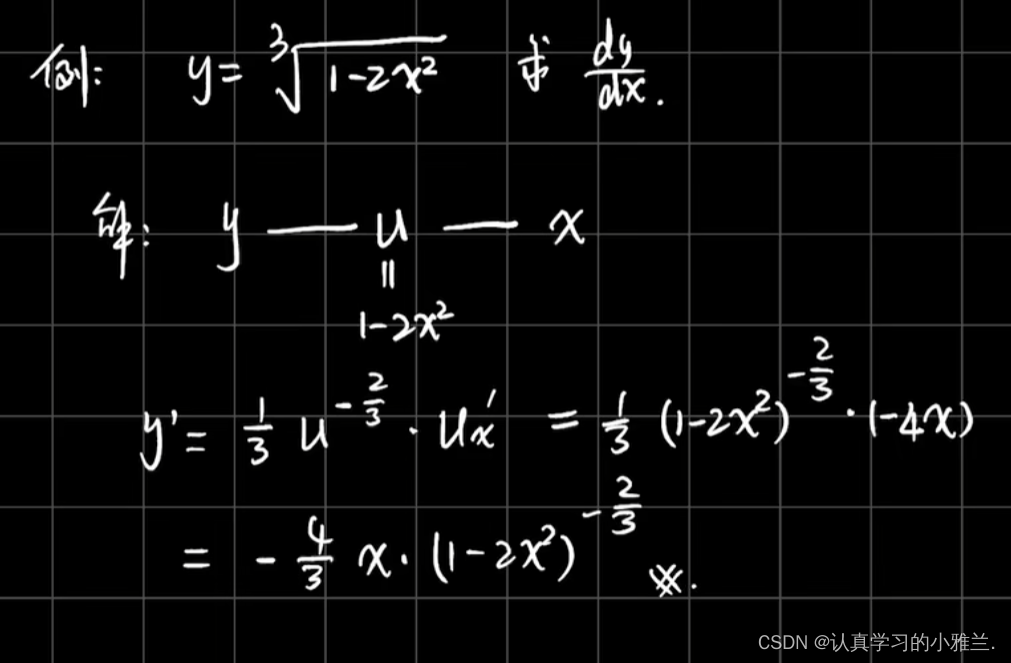
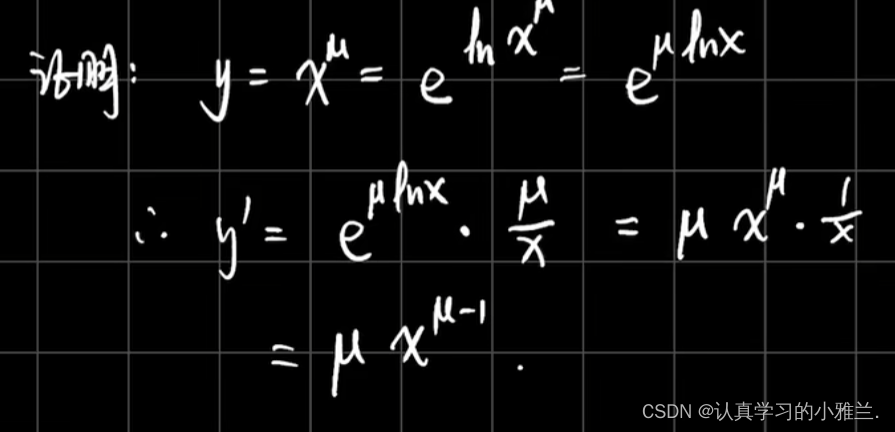
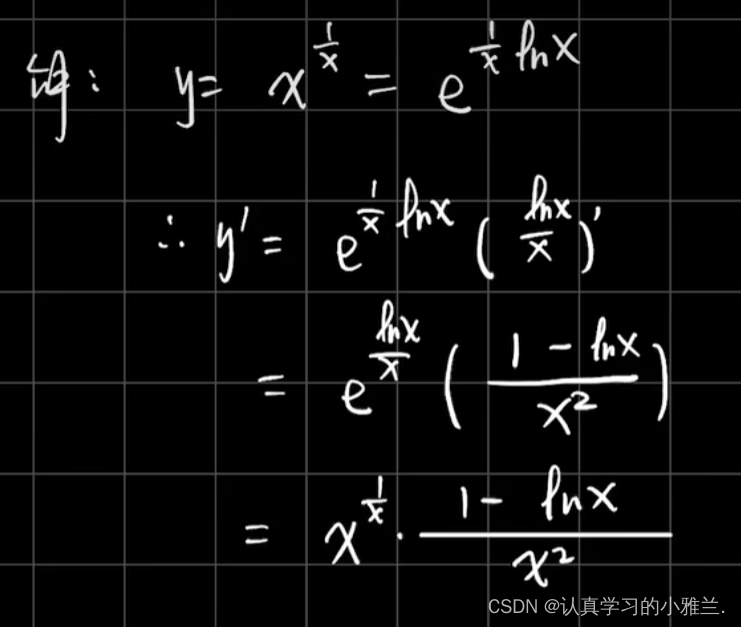
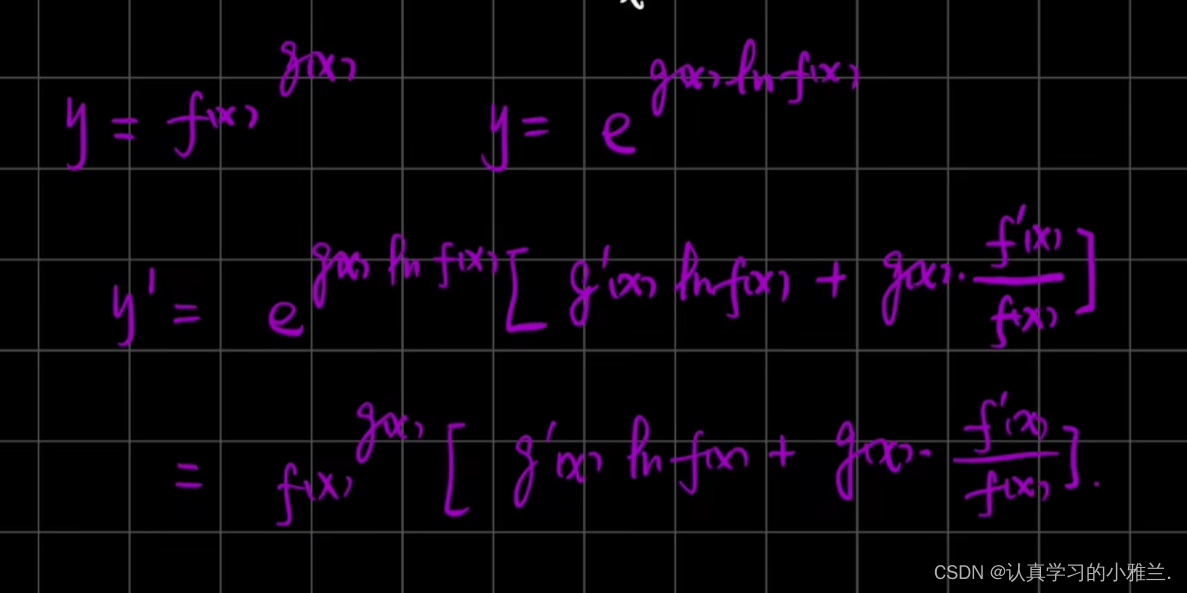
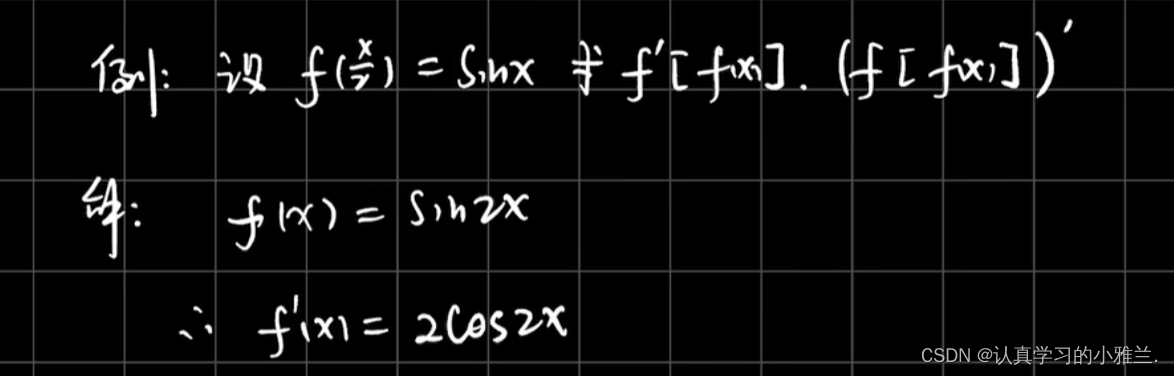
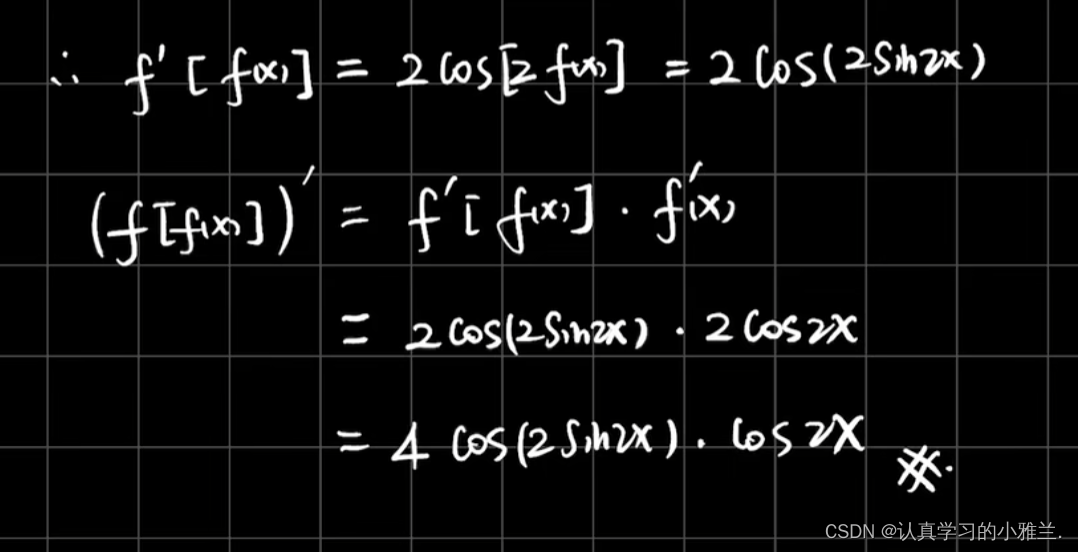
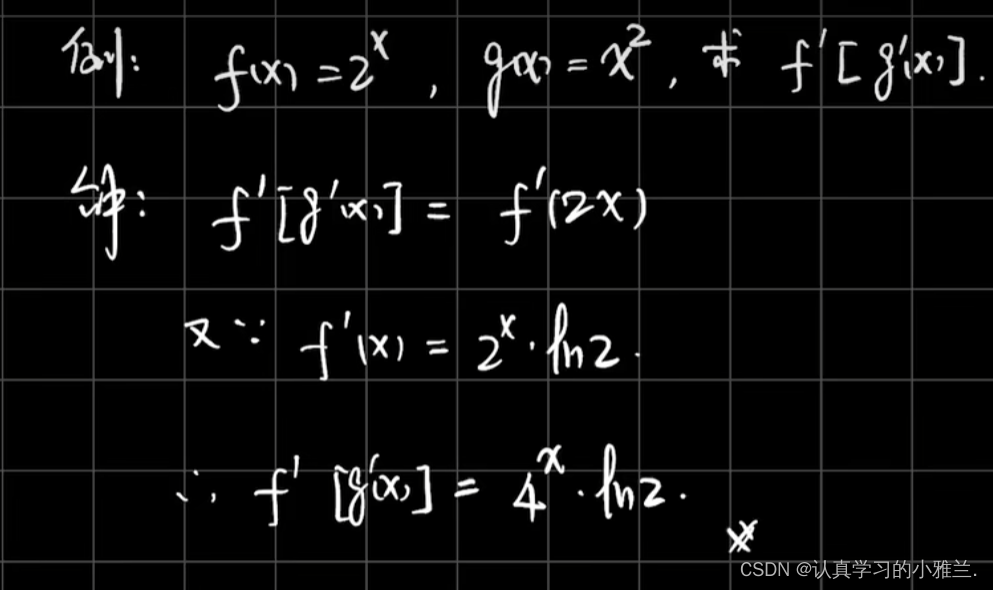
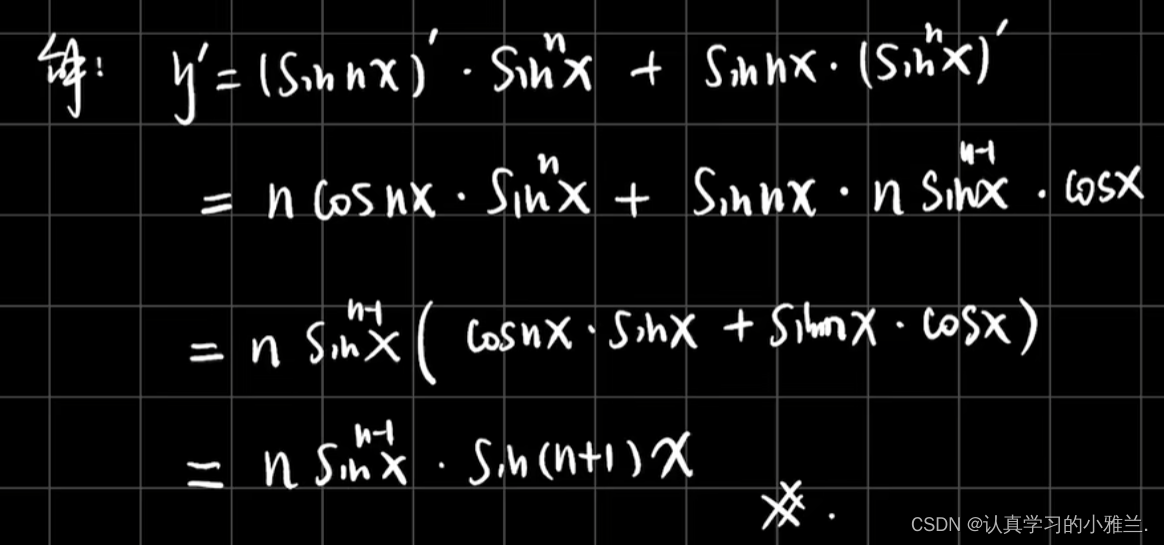
好啦，小雅兰今天的内容就到这里了，其实这篇博客，总体内容来说都是我们高中学习过的知识，只是我把这些以前背的结论性的东西证明了一下，并用了大量的例题来说明这些结论，这篇博客主要讲了函数的和、差、积、商的求导法则、反函数的求导法则和复合函数的求导法则，内容不难，但还是得认真学习，uu们一起加油呀！！！
