LSS论文与代码详解

本文首发于公众号【DeepDriving】，欢迎关注。

0. 前言

最近几年，BEV感知是自动驾驶领域中一个非常热门研究方向，其核心思想是把多路传感器的数据转换到统一的BEV空间中去提取特征，实现目标检测、地图构建等任务。如何把多路相机的数据从二维的图像视角转换到三维的BEV视角？LSS提出一种显示估计深度信息的方法，实现图像特征到BEV特征的转换，从而实现语义分割任务。

LSS是英伟达在ECCV2020上发表的文章《Lift, Splat, Shoot: Encoding Images from Arbitrary Camera Rigs by Implicitly Unprojecting to 3D》中提出的一个BEV感知算法，后续很多BEV感知算法如CaDDN、BEVDet都是在LSS的基础上实现的。本文将结合论文和代码详细解读LSS的原理。

1. 核心思想

作者提出一种新的端到端架构，该架构可以从任意数量的相机中直接提取给定图像数据场景中的鸟瞰图（bird’s-eye-view，BEV）表示，其核心思想是将每张图像单独“提升（Lift）”到每个相机的特征视锥体中，然后将所有视锥体“溅射（Splat）”到栅格化的BEV网格中。结果表明，这样训练的模型不仅能够学习如何表示图像特征，还能够学习如何将来自全部相机的预测结果融合到单个内聚的场景表示中，同时对标定误差具有鲁棒性。在基于BEV的目标分割和地图分割等任务中，该模型都比之前的模型表现得更出色。

2. 算法原理

在自动驾驶中，通常会在车身周围安装多个传感器（相机、雷达等）以使车辆具备360°感知能力。每个传感器都有自己的一个坐标系，它们的输出数据或者感知结果最终会被汇总到一个统一的坐标系——自车坐标系进行处理。通过标定，我们可以得到车上每个相机的外参矩阵 $E_{k} \in \mathbb{R}^{3\times 4}$ 和内参矩阵 $I_{k} \in \mathbb{R}^{3\times 3}$ 。内、外参矩阵决定了从自车坐标系 $(x, y, z)$ 到图像坐标系 $(h, w, d)$ 的映射关系。对于从各个相机获取的 $n$ 张图片 $\left \{ X_{k} \in \mathbb{R}^{3\times H\times W}\right \}_{n}$ ，LSS算法的目的是在BEV坐标系 $y\in \mathbb{R}^{C\times X \times Y}$ 中找到该场景的栅格化表示，然后在该表示的基础上实现目标分割、地图分割等感知任务。

LSS算法分为3个步骤：Lift，Splat，Shoot。

2.1 Lift: 潜在的深度分布

这一步的目的是把每个相机的图像从局部2D坐标系Lift到全部相机共享的统一3D坐标系，这个操作过程每个相机是独立进行的。

众所周知，从二维图像中看到的物体是没有深度信息的，所以从图像上我们不知道这些物体在三维空间中的实际位置和大小。为了解决深度信息缺失的问题，LSS算法提出的解决方案是在所有可能的深度上为每个像素生成一个表示。假设一个相机的图像表示为 $X\in \mathbb{R}^{3 \times H \times W}$ ，它的内、外参矩阵分别为 $I$ 和 $E$ ，像素 $p$ 在图像坐标系中的坐标为 $(h, w)$ 。对于图像中的每个像素 $p$ ，作者使用$\left | D \right | $个点$ \left { (h,w,d)\in \mathbb{R} ^{3} \right } $与像素进行关联，其中$ D $表示一组离散的深度值，定义为$ \left { d_{0}+\Delta ,\dots ,d_{0}+\left | D \right |\Delta \right } $。通过这种方式，就为每个相机的图像创建了数量为$ D \times H \times W$的点云，这个过程只跟相机的内外参有关，并没有可学习的参数。

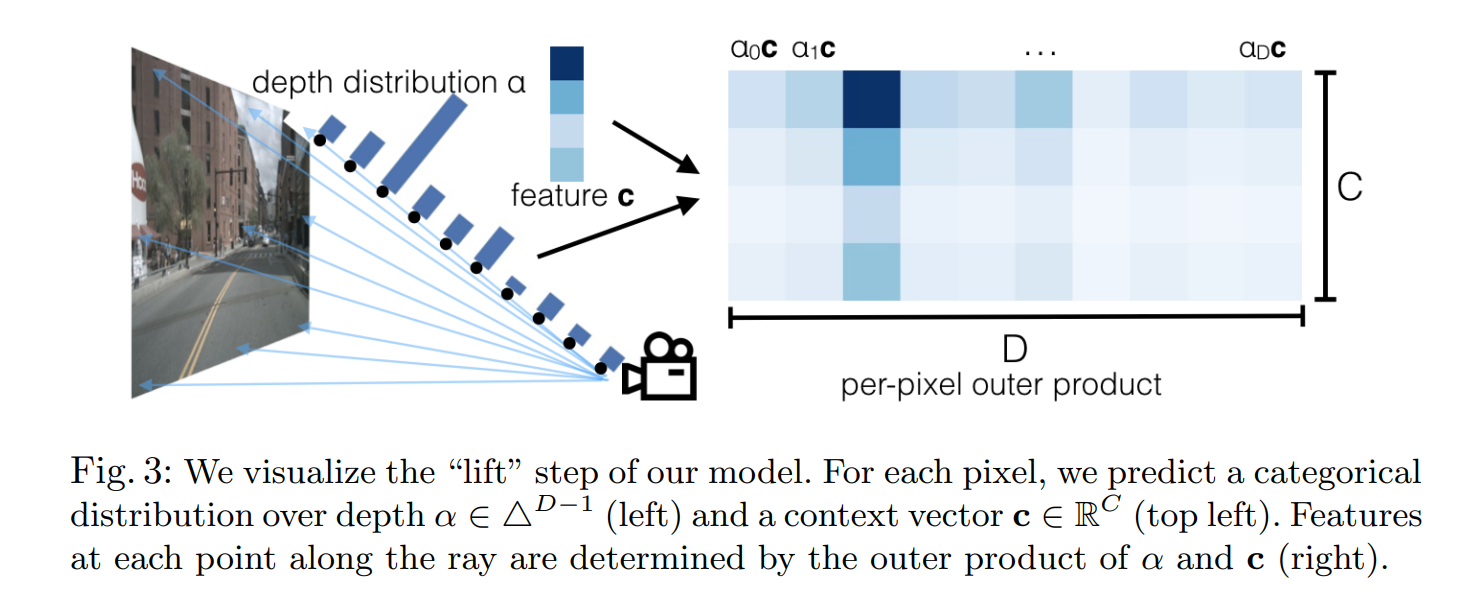
在像素点 $p$ ，模型会预测一个上下文向量 $\mathbf{c} \in \mathbb{R}^{C}$ 和每个像素在深度上的分布 $\alpha \in \Delta^{\left | D \right |-1}$ ，与点 $p_{d}$ 关联的上下文特征向量 $c_{d} \in \mathbb{R}^{C}$ 定义为 $\mathbf{c}_{d}=\alpha_{d}\mathbf{c}$ 。

总的来说，Lift这个操作是为每个相机的图像生成大小为 $\times H \times W$ 空间位置查询，这个空间中的每个点对应一个上下文特征向量 $c_{d} \in \mathbb{R}^{C}$ 。在相机的可视范围内，这个空间是一个视椎体。

2.2 Splat：Pillar池化

作者采用与pointpillars算法中一样的方式处理Lift操作生成的点云，一个Pillar定义为无限高度的体素。每个点被分配到与其最近的Pillar中然后执行求和池化，产生一个可以被标准CNN处理的 $C\times H \times W$ 维度的张量。

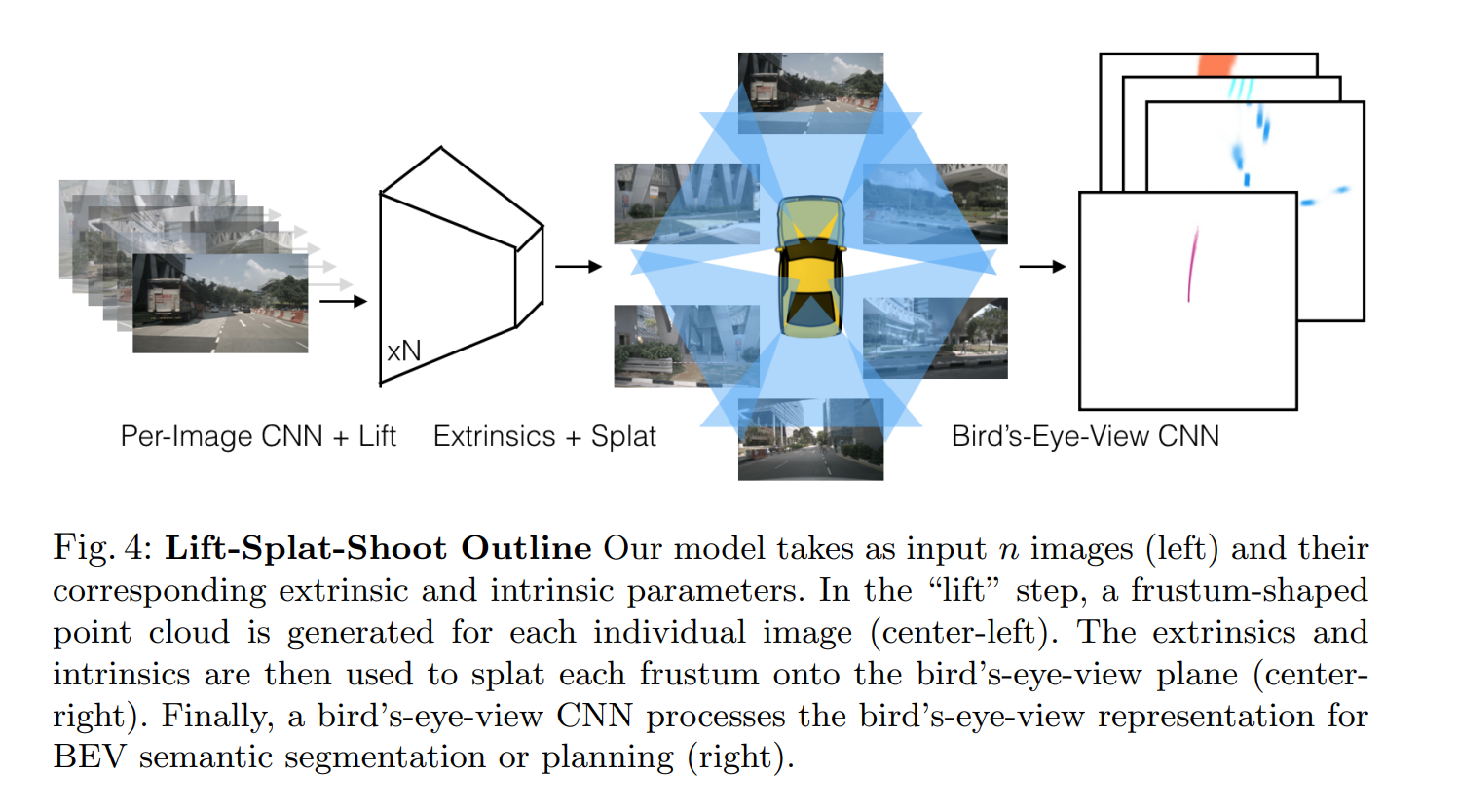
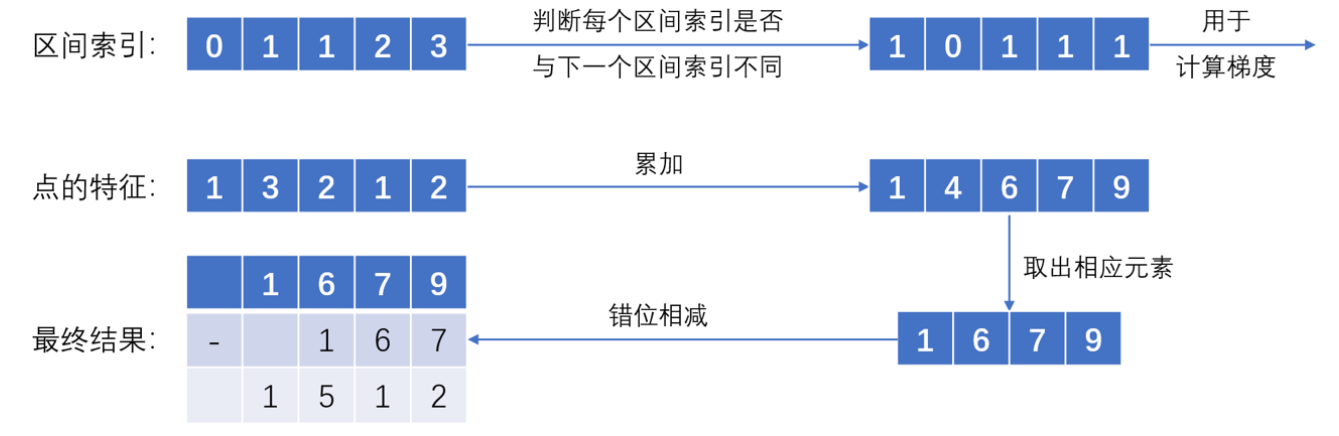
为了提升效率，作者采用“累计求和”的方式实现求和池化，而不是等填充完每个Pillar后再来做池化。这种操作具有可分析的梯度，可以高效地计算以加速自动微分过程。由于Lift操作生成的点云坐标只与相机的内外参有关，因此可以预先给每个点分配一个索引，用于指示其属于哪个Pillar。对所有点按照索引进行排序，累积求和的具体实现过程如下：

图片来源于深蓝学院《BEV感知理论与实践》

2.3 Shoot：运动规划

这个操作是根据前面BEV空间的感知结果学习端到端的轨迹预测代价图用于运动规划。由于我们主要关注感知部分，这部分就不做过多介绍。

3. 代码解析

如果只看论文，估计很多人看完论文后还是一头雾水，根本不知道LSS到底是怎么实现的。接下来我们就结合代码对LSS的每个步骤进行详细解析。

LSS模型被封装在src/model.py文件中的LiftSplatShoot类中，模型用Nuscense数据集进行训练，每次输入车身环视6个相机的图像。Nuscense数据集中的原始图像宽高为1600x900，在预处理的时候被缩放到352x128的大小，6个相机的图像经过预处理后组成一个维度为(B=1,N=6,C=3,H=128,W=352)的张量输入给LSS模型。前向推理时，LiftSplatShoot类的forward函数需要输入以下几个参数：

x: 6个相机的图像组成的张量，(1,6,3,128,352)
rots: 6个相机从相机坐标系到自车坐标系的旋转矩阵，(1,6,3,3)
trans: 6个相机从相机坐标系到自车坐标系的平移向量，(1,6,3)
intrins: 6个相机的内参矩阵，(1,6,3,3)
post_rots: 6个相机的图像因预处理操作带来的旋转矩阵，(1,6,3,3)
post_trans: 6个相机的图像因预处理操作带来的平移向量，(1,6,3)

LSS模型前向推理的大致流程如下图所示：

外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传

在LiftSplatShoot类的初始化函数中，会调用create_frustum函数去为相机生成图像坐标系下的视锥点云，维度为（D=41,H=8,W=22,3），其中D表示深度方向上离散深度点的数量，3表示每个点云的坐标[h,w,d]。

def create_frustum(self):
    # make grid in image plane
    # 模型输入图片大小，ogfH：128, ogfW:352
    ogfH, ogfW = self.data_aug_conf['final_dim']
    # 输入图片下采样16倍的大小，fH：8, fW:22
    fH, fW = ogfH // self.downsample, ogfW // self.downsample
    # ds取值范围为4~44，采样间隔为1
    ds = torch.arange(*self.grid_conf['dbound'], dtype=torch.float).view(-1, 1, 1).expand(-1, fH, fW)
    D, _, _ = ds.shape
    # xs取值范围为0~351，在该范围内等间距取22个点，然后扩展维度，最终维度为(41,8,22)
    xs = torch.linspace(0, ogfW - 1, fW, dtype=torch.float).view(1, 1, fW).expand(D, fH, fW)
    # ys取值范围为0~127，在该范围内等间距取8个点，然后扩展维度，最终维度为(41,8,22)
    ys = torch.linspace(0, ogfH - 1, fH, dtype=torch.float).view(1, fH, 1).expand(D, fH, fW)

    # D x H x W x 3
    # frustum维度为（41,8,22,3）
    frustum = torch.stack((xs, ys, ds), -1)
    return nn.Parameter(frustum, requires_grad=False)

在推理阶段，会根据相机的内外参把图像坐标系下的视锥点云转换到自车坐标系下，这个过程在get_geometry函数中实现：

def get_geometry(self, rots, trans, intrins, post_rots, post_trans):
    B, N, _ = trans.shape

    # undo post-transformation
    # B x N x D x H x W x 3
    # 首先抵消因预处理带来的旋转和平移
    points = self.frustum - post_trans.view(B, N, 1, 1, 1, 3)
    points = torch.inverse(post_rots).view(B, N, 1, 1, 1, 3, 3).matmul(points.unsqueeze(-1))

    # 坐标系转换过程：图像坐标系 -> 相机坐标系 ->自车坐标系

    # points[:, :, :, :, :, :2]表示图像坐标系下的(h,w)，points[:, :, :, :, :, 2:3]为深度d
    points = torch.cat((points[:, :, :, :, :, :2] * points[:, :, :, :, :, 2:3],
                        points[:, :, :, :, :, 2:3]
                        ), 5)
    # 首先乘以内参的逆转到相机坐标系，再由相机坐标系转到自车坐标系
    combine = rots.matmul(torch.inverse(intrins))
    points = combine.view(B, N, 1, 1, 1, 3, 3).matmul(points).squeeze(-1)
    points += trans.view(B, N, 1, 1, 1, 3)

    return points

要想看懂这个函数中关于坐标系转换的代码，我们需要了解不同坐标系之间的关系。

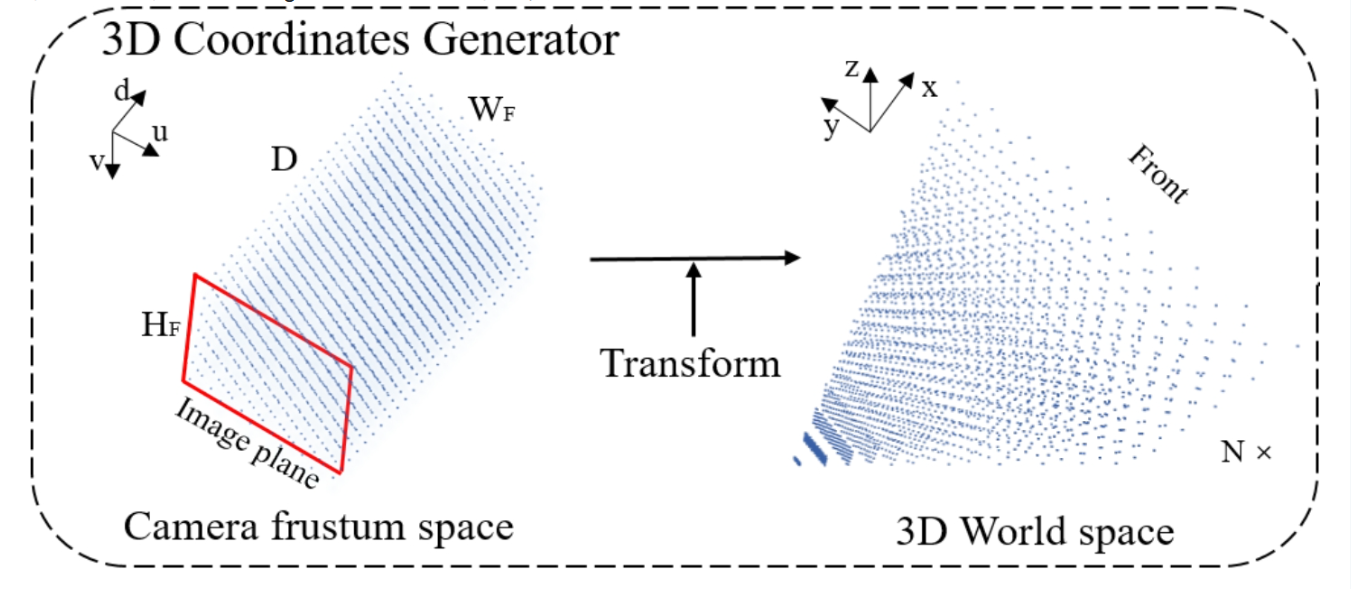
图片来源于深蓝学院《BEV感知理论与实践》

假设用 $K$ 表示相机内参矩阵， $d$ 表示三维点 $P$ 在相机坐标系下的深度，该点在图像坐标系下的坐标为 $u,v,d)^{T}$ ，那么该点在相机坐标系下的坐标 $X_{c},Y_{c},Z_{c})^{T}$ 可以表示为：

$\begin{pmatrix} X_{c} \\ Y_{c} \\ Z_{c} \end{pmatrix}=K^{-1}\begin{pmatrix} ud \\ vd \\ d \end{pmatrix}$

用 $R$ 表示由相机坐标系转换到自车坐标系的旋转矩阵， $\mathbf{t}$ 表示由相机坐标系转换到自车坐标系的平移向量，那么自车坐标系下的点 $X_{ego},Y_{ego},Z_{ego})^{T}$ 可以表示为：

$\begin{pmatrix} X_{ego} \\ Y_{ego} \\ Z_{ego} \end{pmatrix}=R\begin{pmatrix} X_{c} \\ Y_{c} \\ Z_{c} \end{pmatrix}+\mathbf{t}$

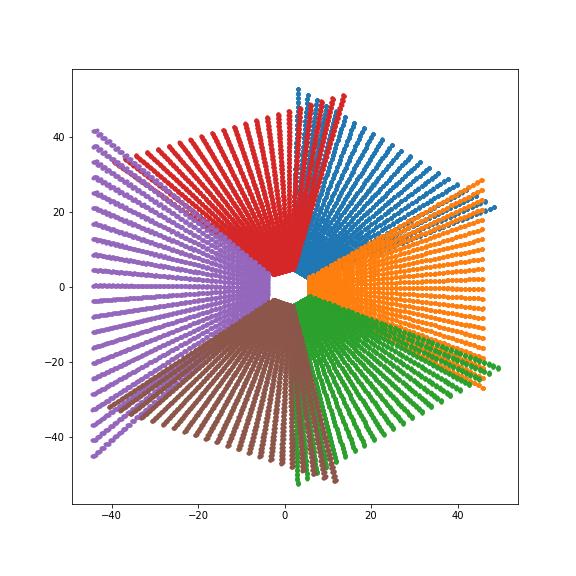
如果把经过上述转换的点云在BEV空间下进行可视化，可以得到类似下面的图：

说完了视锥点云的创建与变换过程，我们再来看一下模型对输入图像数据的处理。由6个相机的图像组成的张量x的维度为(1,6,3,128,352)，推理时首先把维度变换为(1 * 6,3,128,352)，然后送入camencode模块中进行处理。在camencode模块中，图像数据首先被送入EfficientNet-B0网络中去提取特征，该网络输出的两层特征x1和x2的维度分别为(6,320,4,11)和(6,112,8,22)。接下来，x1和x2被送入到Up模块中进行处理。在该模块中，对x1进行上采样把维度变为(6,320,8,22)，然后与x2拼接到一起，最后经过两层卷积处理，输出维度为(6,512,8,22)的张量。这个张量再经过一个核大小为1x1的卷积层depthnet处理，输出的维度为(6,105,8,22)。在这105个通道中，其中前41个会用SoftMax函数求取表示41个离散深度的概率，另外64个通道则表示前面说过的上下文向量，这41个深度概率与64个上下文特征向量会做一个求外积的操作。整个camencode模块输出的张量维度为(6,64,41,8,22)，最终这个张量的维度会被变换为(1,6,41,8,22,64)。（这段文字对照上面的流程图来看效果会更好）

到这里，Lift这部分的操作就讲完了，接下来我们来看Splat。

Splat操作的第一步是构建BEV空间下的特征，这个过程在voxel_pooling函数中实现。该函数有两个输入，一个自车坐标系下的视锥点云坐标点geom，维度为(1,6,41,8,22,3)；另一个是camencode模块输出的图像特征点云x，维度为(1,6,41,8,22,64)。voxel_pooling函数的处理过程如下：

1. 将x的维度变换为(1 * 6 * 41 * 8 * 22,64)；
1. 将geom转换到体素坐标下，得到对应的体素坐标，并将参数范围外的点过滤掉；
1. 将体素坐标系下的geom的维度变换为(1 * 6 * 41 * 8 * 22,3)，然后给每个点分配一个体素索引，再根据索引值对geom和x进行排序，这样归属于同一体素的点geom及其对应的特征向量x就会被排到相邻的位置；
1. 用累计求和的方式对每个体素中的点云特征进行求和池化；
1. 用unbind对张量沿Z维度进行分离，然后将分离的张量拼接到一起进行输出。由于Z维度的值为1，这样做实际上是去掉了Z维度，这样BEV空间下的特征就构建好了。下图是对BEV特征做可视化的结果：

def voxel_pooling(self, geom_feats, x):
    B, N, D, H, W, C = x.shape
    Nprime = B*N*D*H*W

    # 将特征点云展平，共有B*N*D*H*W个点，每个点包含C维特征向量
    x = x.reshape(Nprime, C)

    # 把自车坐标系下的坐标转换为体素坐标，然后展平
    geom_feats = ((geom_feats - (self.bx - self.dx/2.)) / self.dx).long()
    geom_feats = geom_feats.view(Nprime, 3)
    # 求每个点对应的batch size
    batch_ix = torch.cat([torch.full([Nprime//B, 1], ix,
                            device=x.device, dtype=torch.long) for ix in range(B)])
    geom_feats = torch.cat((geom_feats, batch_ix), 1)

    # 过滤点范围外的点
    kept = (geom_feats[:, 0] >= 0) & (geom_feats[:, 0] < self.nx[0])\
        & (geom_feats[:, 1] >= 0) & (geom_feats[:, 1] < self.nx[1])\
        & (geom_feats[:, 2] >= 0) & (geom_feats[:, 2] < self.nx[2])
    x = x[kept]
    geom_feats = geom_feats[kept]

    # 求每个点对应的体素索引，并根据索引进行排序
    ranks = geom_feats[:, 0] * (self.nx[1] * self.nx[2] * B)\
        + geom_feats[:, 1] * (self.nx[2] * B)\
        + geom_feats[:, 2] * B\
        + geom_feats[:, 3]
    sorts = ranks.argsort()
    x, geom_feats, ranks = x[sorts], geom_feats[sorts], ranks[sorts]

    # 累计求和，对体素中的点进行求和池化
    if not self.use_quickcumsum:
        x, geom_feats = cumsum_trick(x, geom_feats, ranks)
    else:
        x, geom_feats = QuickCumsum.apply(x, geom_feats, ranks)

    # final：(B x C x Z x X x Y)，(1 x 64 x 1 x 200 x 200)
    final = torch.zeros((B, C, self.nx[2], self.nx[0], self.nx[1]), device=x.device)
    # 把特征赋给对应的体素中
    final[geom_feats[:, 3], :, geom_feats[:, 2], geom_feats[:, 0], geom_feats[:, 1]] = x

    # 去掉Z维度
    final = torch.cat(final.unbind(dim=2), 1)

    # final：(1,64,200,200)
    return final