布尔运算00

news2024/10/6 8:29:52

题目链接

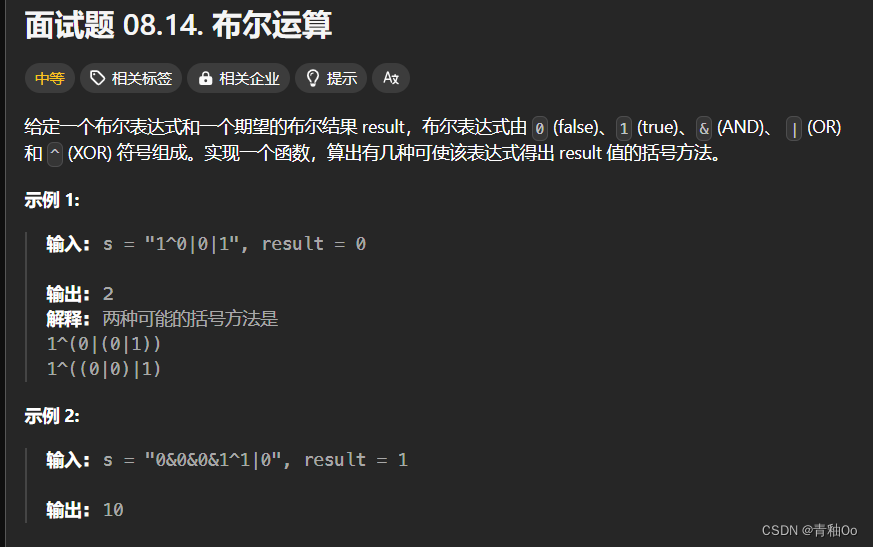
布尔运算

题目描述

注意点

运算符的数量不超过 19 个
布尔表达式由 0 (false)、1 (true)、& (AND)、 | (OR) 和 ^ (XOR) 符号组成
算出有几种可使该表达式得出 result 值的括号方法

解答思路

可以使用动态规划根据左右两侧区间不同结果相应组合数量计算得出当前区间不同结果相应组合数量，dp[i][j][k]表示第i个到第j个数字组合结果为k的组合数量
初始先将dp[i][i][s.charAt(i) - ‘0’]设置为1
三重循环计算dp[0][s.length() - 1][result]的值：第一重循环枚举区间长度为len时不同结果相应的组合数量；第二重枚举所有区间长度为len的不同区间中不同结果相应的组合数量；第三重循环枚举[i, j]的区间内所有的组合并计算组合相应结果的数量

代码

class Solution {
    public int countEval(String s, int result) {
        int n = s.length();
        // dp[i][j][k]表示第i个到第j个数字组合结果为k的组合数量
        int[][][] dp = new int[n][n][2];
        // 初始将每个位置的数字写到dp中
        for (int i = 0; i < n; i += 2) {
            dp[i][i][s.charAt(i) - '0'] = 1;
        }
        // 第一重循环枚举区间长度为len时不同结果相应的组合数量，每次跳两格方便找到下一个数字
        for (int len = 2; len < n; len += 2) {
            // 第二重枚举所有区间长度为len的不同区间中不同结果相应的组合数量
            for (int i = 0; i < n - len; i += 2) {
                int j = i + len;
                // 第三重循环枚举[i, j]的区间内所有的组合，组合数量可根据符号左右两侧的数字组合数量推出
                for (int k = i; k < j; k += 2) {
                    char operate = s.charAt(k + 1);
                    if (operate == '&') {
                        // 结果为0左右有一侧为0即可
                        dp[i][j][0] += dp[i][k][0] * dp[k + 2][j][0] + dp[i][k][0] * dp[k + 2][j][1] + dp[i][k][1] * dp[k + 2][j][0];
                        // 结果为1必须左右两侧都为1
                        dp[i][j][1] += dp[i][k][1] * dp[k + 2][j][1];
                    }
                    if (operate == '|') {
                        // 结果为0必须左右两侧都为0
                        dp[i][j][0] += dp[i][k][0] * dp[k + 2][j][0];
                        // 结果为1左右有一侧为1即可
                        dp[i][j][1] += dp[i][k][1] * dp[k + 2][j][1] + dp[i][k][0] * dp[k + 2][j][1] + dp[i][k][1] * dp[k + 2][j][0];
                    }
                    if (operate == '^') {
                        // 结果为0左右侧都为0或者左右侧都为1
                        dp[i][j][0] += dp[i][k][0] * dp[k + 2][j][0] + dp[i][k][1] * dp[k + 2][j][1];
                        // 结果为1左右侧有一侧为0，另一侧为1
                        dp[i][j][1] += dp[i][k][1] * dp[k + 2][j][0] + dp[i][k][0] * dp[k + 2][j][1];
                    }
                }
                
            }
        }
        return dp[0][n - 1][result];
    }
}