一个简单的问题:
如果此时你正站在迷路缭绕的山坡上,能见度不高,但是你又想去往最低的山谷的位置,怎么走?

很简单,哪里陡那就往那里走呗——而这就是梯度下降算法的思想。
古话说:“先发制于人,后发而制于人。”
想要做到有效先发呢,就得做到对事务的准确预测,要预测就得先掌握其规律。规律从哪里来?当然是从数据上来,所以关键就是要找到数据与数据之间的关联。
比如气温越高,雪糕的销售额也就越高,这个就是数据与数据之间的关联:
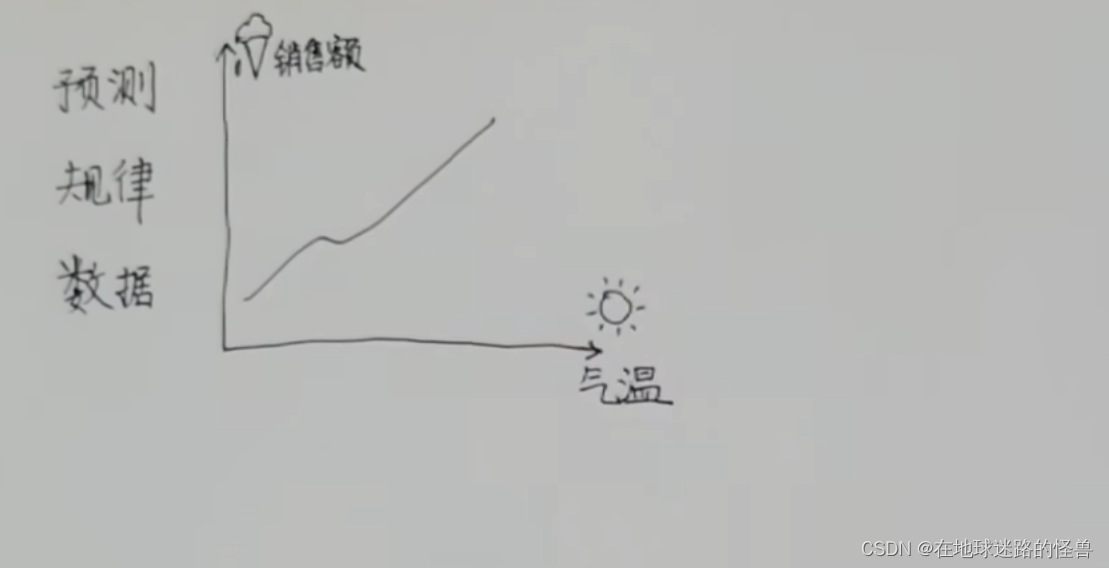
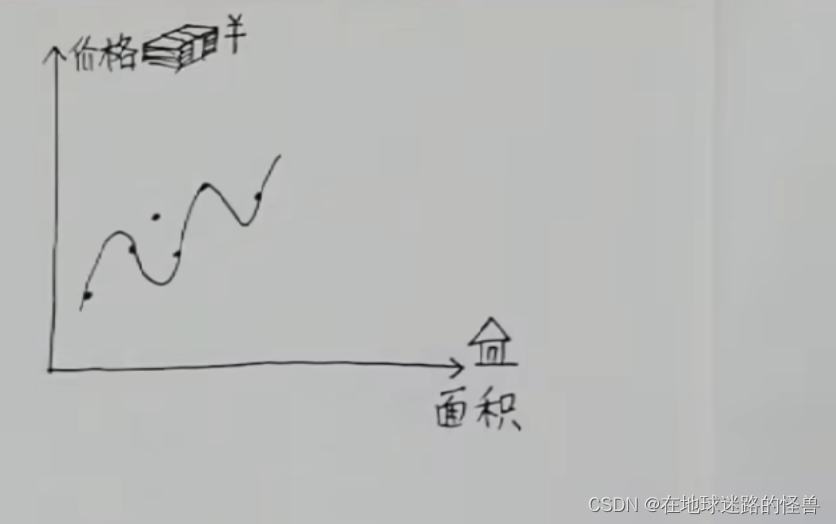
还有一个经典的例子,就是房子价格与面积的关系:

从所给数据不难看出二者是有正相关关系的。
但是要做到准确的预测的话必须要得到它们之间的函数关系式,这样我们只需要给出一个面积值那么立马就能直接得到价格是多少了。
要求函数关系式的话,那么需不需要做一条曲线将坐标系中的所有的点都穿过去呢?明显是不可以的,因为当有新数据再加进来的时候,往往新数据根本就不在这条曲线上:
这样吃力不讨好的行为(勾画曲线),通常叫做过拟合。
对于这种明显有相关关系的数据往往最朴素的方法反而效果更好,直接用一条直线去拟合这些数据:
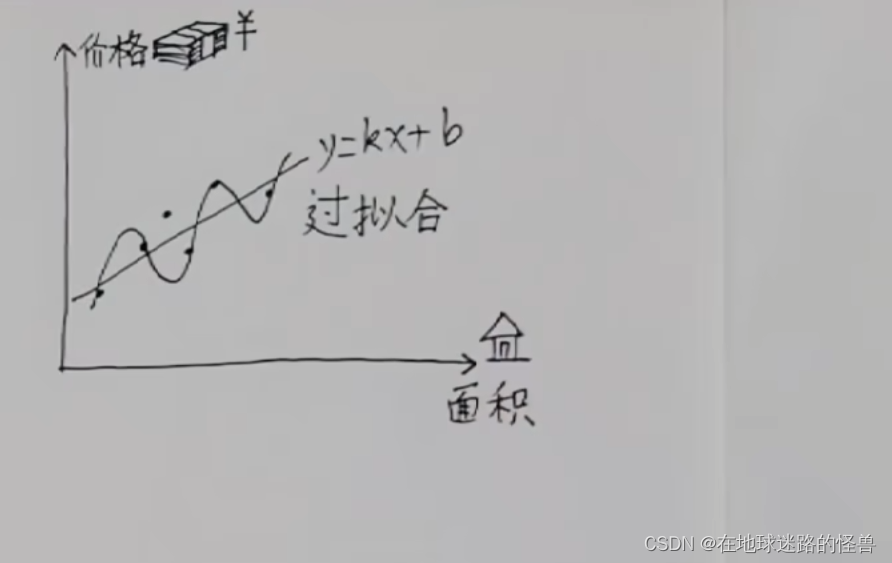
直线的话就好搞了,就是一次函数 y=kx+b 嘛,只要把这条直线的斜率和截距都找到的时候,那么这条直线就自然被找出来了。
而我们找到最合适的这条直线的这些动作,我们就称作线性回归。
那么哪条直线更合适呢?毕竟有那么多:
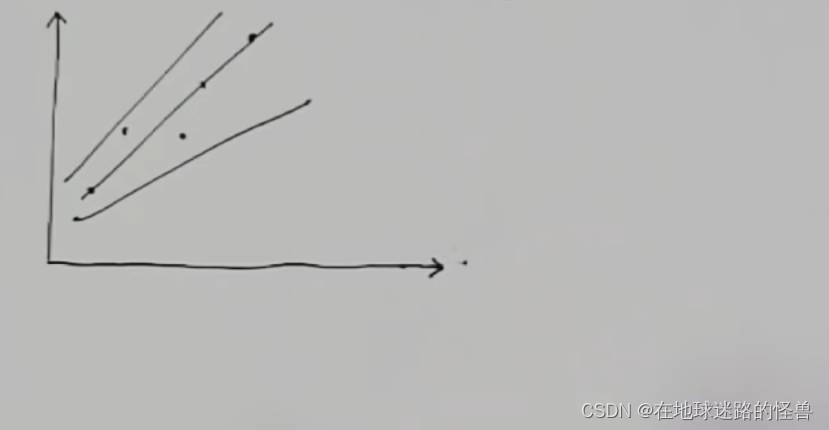
这很难说,那么既然很难决定,那就全部一起考虑,跟选秀一样,到时候留下最合适的那个就可以了。
既然是选秀,那么就会有标准,标准是什么呢?
以下图中的一条黑线和红线为例,这两条都是拟合真实数据出来的直线(二者都是理想化的估算数据):

不难看出二者与真实数据之间都是有差距的,但我们可以把每个点的真实数据和估算数据的误差给算出来,在图上可以表现为真实数据竖直到这条线的距离是多长:
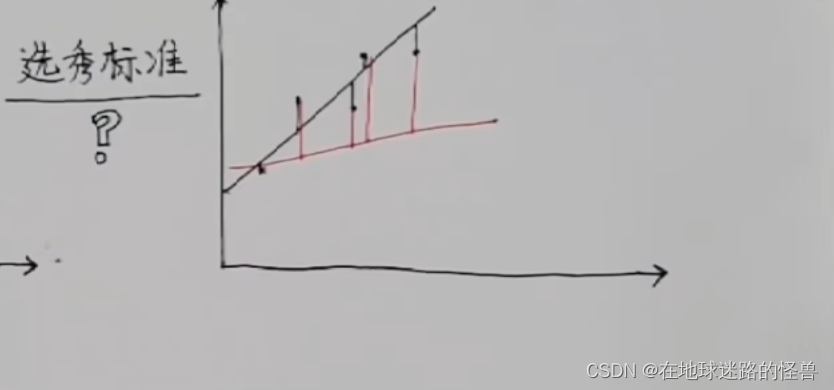
可以明显看到,黑线的距离之和是要比红线的距离之和要短的,那么我们就可以认为黑线更优秀,和原数据更加符合。
接下来使用数学语言来描述一下这个事情:
假如真实数据是 y1, y2, y3, y4, y5,而估算数据是 y^ = kx+b:
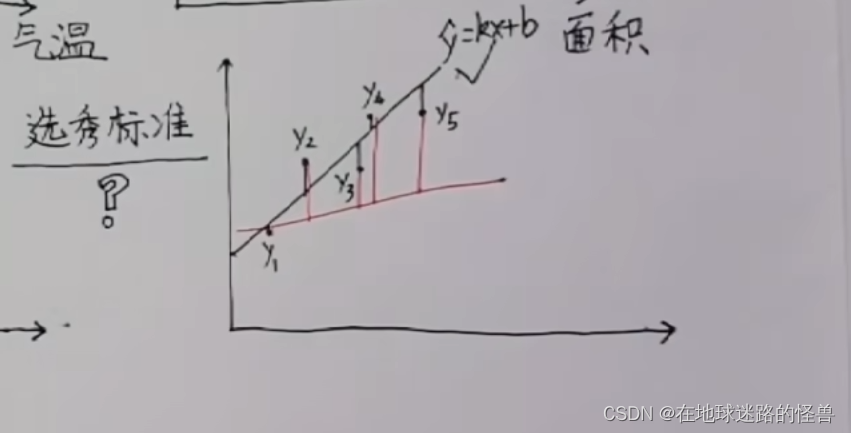
那么其距离之和可以表示为:
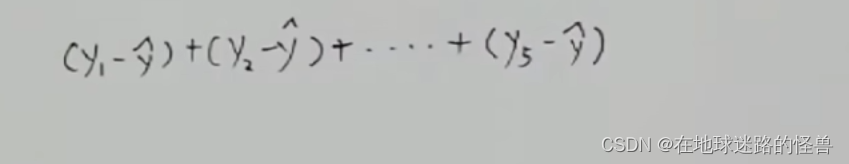
但是此时有一个问题,点在线上方的距离算出来是正的,而点在线下方算出来的距离呢则是负值:

一正一负相加是会抵消掉一些距离的,那么算出来的结果肯定就会出问题,为了消除正负距离带过来的影响,我们可以对每一项进行取平方的操作:
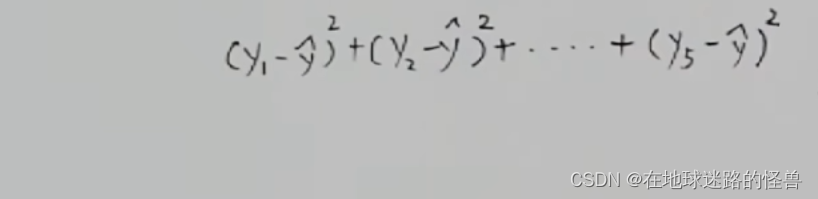
这样再加起来就正确了,这同样可以反映出距离之和的大小。
但还有一个新的问题,假如红线不取五个点,而是取十个点怎么办?因为取的点越多那么累加的距离的平方和肯定就越大,所以在取样点的数量不一样的时候是根本没办法比较的,这怎么办?答案就是对他们取平均,主打一个众生平等:
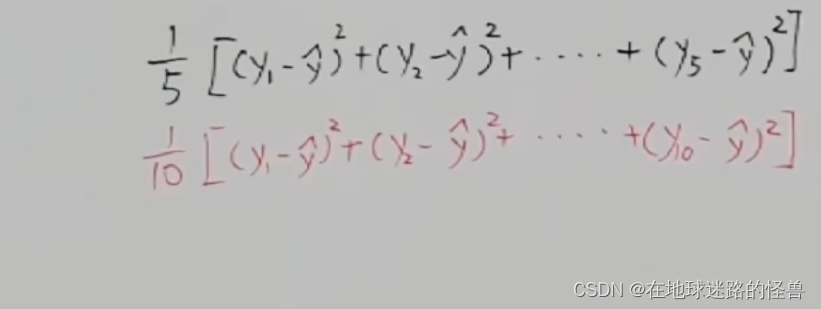
这样取平均之后就可以进行比较了,那么这样的话选秀的标准也就自然出来了:

上面这个值谁求出来的小,那么谁的线就和原数据符合的越好。其还有另外一个名称:平均平方误差MSE。
想要解决一负一正相加抵消的问题,那在这里不取平方取绝对值可以吗?
当然可以,取绝对值的方式叫做平均绝对误差MAE:
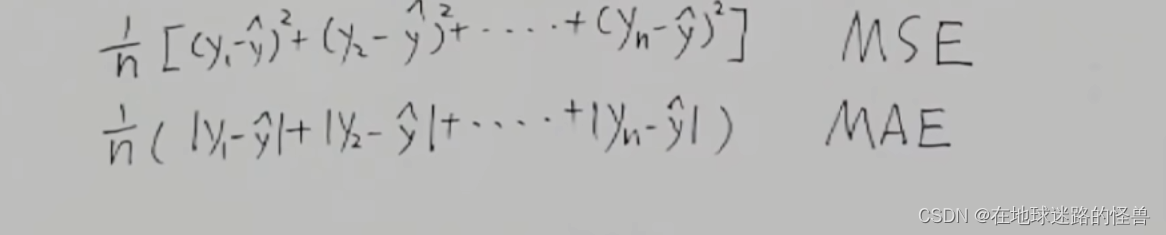
二者在不同的场景之下有不同的优缺点,但是对于梯度下降呢我们一般使用MSE,因为MSE的数学性质更好一些(肯定比求绝对值好算啊)。
在上面的情况中,在少数几条直线的情况下,可以一眼就看出来或者说是稍微的计算一下就可以得出来拟合的较好的直线,但是如果候选者有无数多个,怎么办呢?
简单列个表可能更清晰一些:

我们的任务就是把所有的这个MSE的值全算出来然后挑出来最小的那一个 Zmin,而最小的那一个它所对应的 k 值和 b 值就是你要找的直线了。
上面的过程简单说就是通过一个 k 一个 b 值来计算 MSE 值 z,而这不就是一个以 k 和 b 为自变量,z 为函数值的二元函数吗?
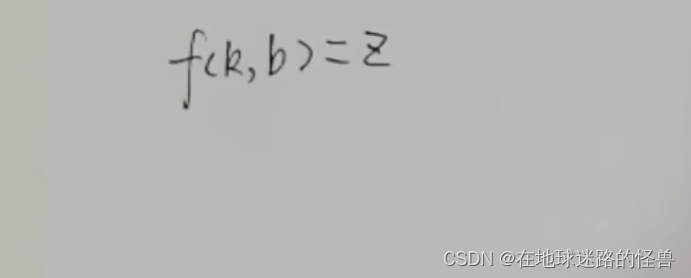
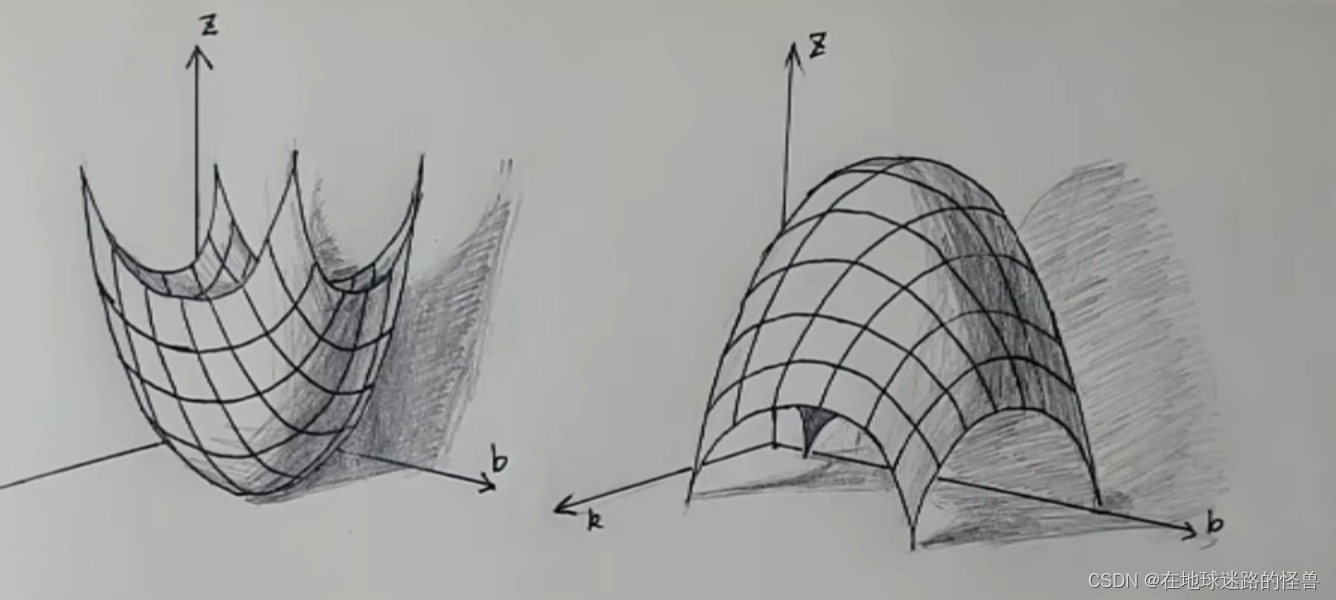
而二元函数长什么样?可以简单的看一下其几何图像:

而这个 f(k , b) = z 这个函数也被称为损失函数,刚刚不是说任务就是要把这些 z 当中的最小值 Zmin 给找出来吗?对应到这个损失函数其实也就是要把这个损失函数的最低的位置找出来。
那么现在我们的任务就变成了找到这个山谷的最低的位置了,要讲明白下山,我们就得从上山讲起:
其实就像地图一样,方便我们定位和指路,如果能有一个像导航一样的上山神器就好了。
还真有!其实就是以前学习过的导数。
我们先看二维坐标系下的导数的相关概念,下图是一个一元函数 f(x),假如现在我们是在 x0 的位置,我们可以对这个点求导数,也就是这个点的切线的斜率,可以看到在 x0 这一点上的导数值是大于 0 的:
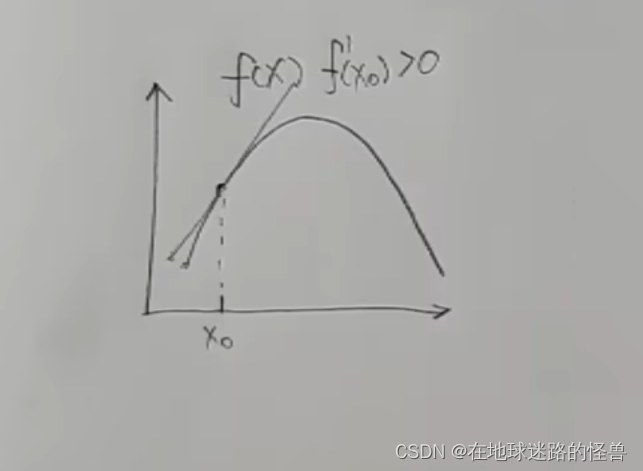
而导数值大于 0 实际上就是在告诉我们这个 x0 要往增大的方向走函数值才能变大才能上坡。
再看一个点 x1,该点上切线斜率实际上是小于零的,这就意味着这个 x1 要往减小的方向去走函数值才能变大才能上坡:
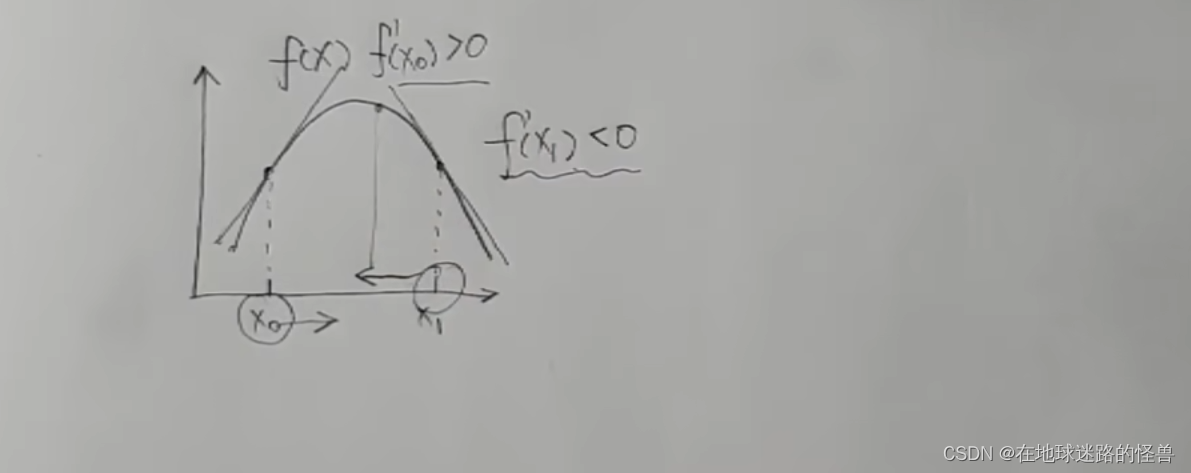
这样一看使用导数值来指明方向还挺好用的,但是只告诉了方向还不太够啊,最好是还能告诉我一步要走多远,然后走到顶了最好还可以叫我停下来这样是最好的。
恰好导数也能够做这个事情。
我们直接拿导数的大小作为步子的长短,假如我们还是在 x0 的这个位置,然后求出这一点的导数是等于二的,那么我们直接拿这个二作为步子的长短,x0 呢就应该要往增大的方向加二来到这个位置对应的函数值。重复这个步骤,随着越来越靠近山顶的位置,坡度就越来越小,那么步子呢也会越来越小,来到山顶的时候导数为零那么直接就是不走了,而这就是我们想要的:

找新落脚点的这个动作我们还可以使用数学语言描述出来,假设现在所在的点是 Xn,对该点求导数将其作为前进的步长就把它直接加上去,得到的结果呢作为下一个点的落脚点:

当然这是一个最理想的状态,万一 X0 这个位置的切线斜率太大了导致跨的步子大了一些,直接一步跨过了山顶的位置来到了对面的位置,不过这也不用慌,因为此时求导数值小于0,它还是会回来的,往复循环最终也能到达山顶:
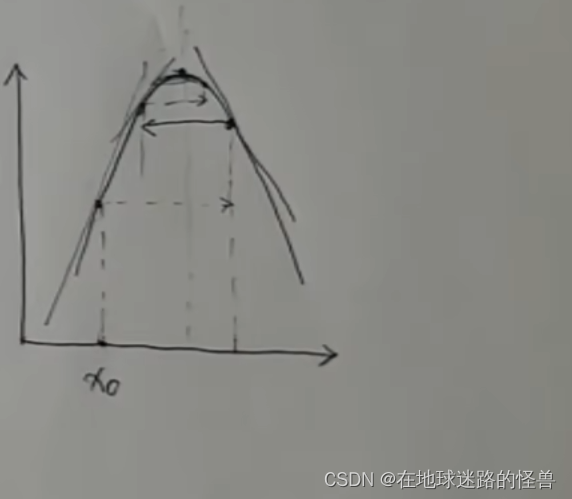
真正麻烦的其实是下面这几种情况,一步刚好跳到了对称的位置,因为是对称的所以求导数再往回跳就又跳回了原来的位置,然后就会一直反复横跳根本停不下来:
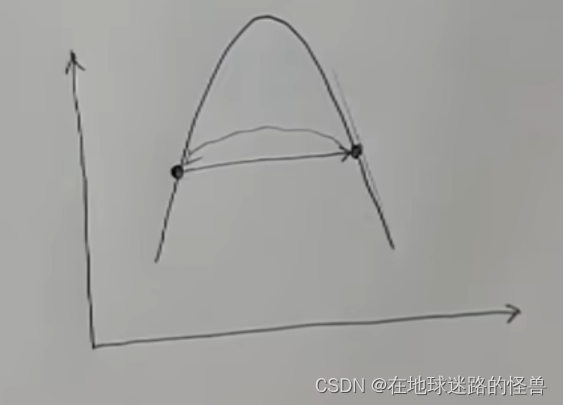
还有一种是从一个位置直接跳到了斜率更大的地方,然后它又会往回跳跳到更远的地方去了,随着循环它就会越跳越远越跳越远然后直接爆炸。
还有这种不止一个山顶的,前面的坡太小导致每一步的步伐也很小,当来到第一个小山顶的时候迈不过去了,你就会以为你已经来到了最高的位置就不走了,陷入了局部最优解:

因此我们在更新位置的时候一般会对这个每一步的长短呢做一个控制,也就是直接在这个导数面前乘以一个系数α,来改变其步长大小。而这个系数,我们又称之为学习率。学习率也不一定是个定值,主要是看你的策略。
那么上面讲的这些个东西是怎么应用到二元函数上面去的呢?
首先不难得知,二元函数的方向有两个,一个是 k 方向,一个是 b 方向,而上山的方向则可以看作是这两个方向的合成。这和地图上是一样的:往东走再往北走,其实等价于往东北方向走嘛:

既然我们要走的方向是上坡,那方向分解到 k 方向和 b 方向呢也应该都是上坡的,如何分解?
假如现在所在的位置是 K0 、B0,它所在的这条经纬线,我们沿着 K 轴的方向看过去,实际上它就是 BOZ 平面上的一条曲线:
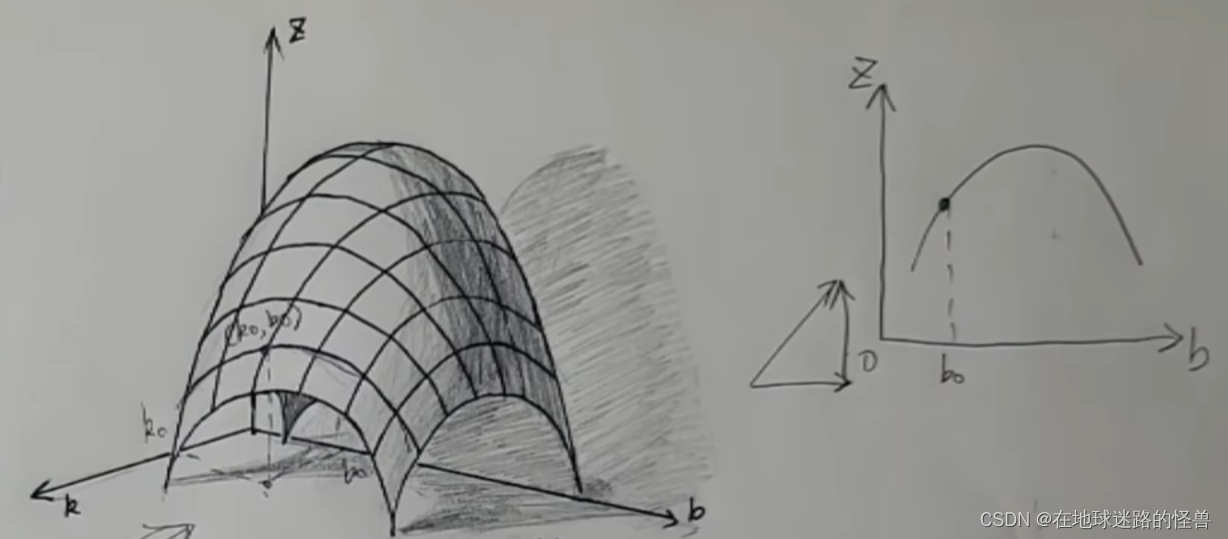
而在 B 的方向上要上坡,那么直接对 B0 这个点求导不就可以了吗?
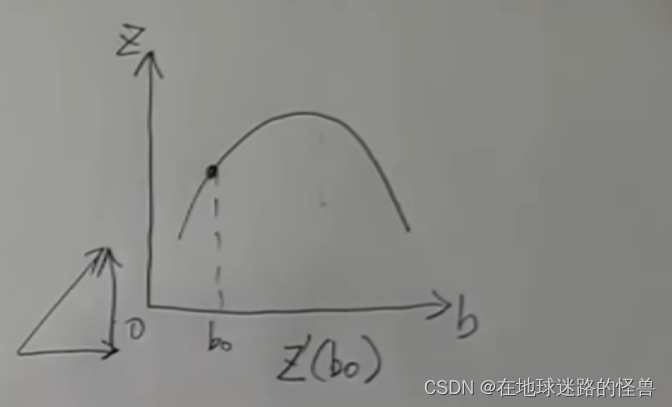
而因为上图中这条线是垂直于这个 K 的方向截出来的,这条线上所有的 K 值都是 K0 不变的,把 K 的值当常数然后再对 B 求导,这不就是对于二元函数来求 B 的偏导吗?然后再把 B = B0 这个点带进去所得的值就是 B 的值的变化量啦:
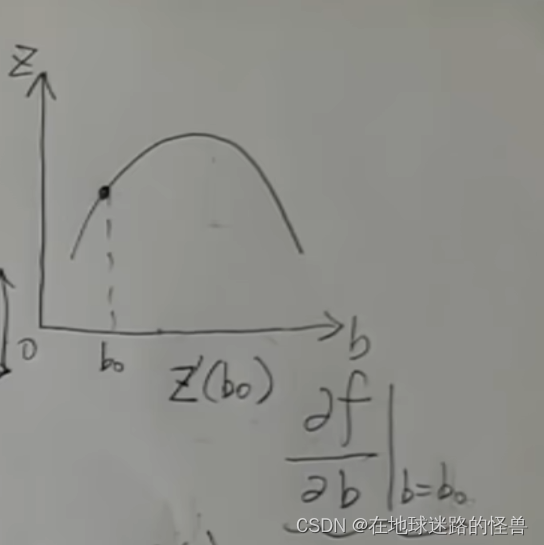
同理对于 K 值的变化量我们只需要换一个方向也就很好求解出来了,也是一个求偏导的操作,然后我们就得到了:

得到的这两个偏导值既告诉了 K 和 B 的方向怎么走,然后呢变化量是多大,所以这个东西不就是一个向量吗?
而这个向量的名字呢,就叫做梯度。
要注意一下,这个梯度指明了 K 方向和 B 方向的变化量,所以梯度应该是这个 KOB 平面上的一个二维向量,怎么理解?用一些具体的数字来看一下吧。
假如现在所在的点是 (1,2),然后求出来梯度的向量呢是(2,3),那么我们的下一个落脚点就应该是 1+2 = 3,2+3 = 5,也就是落脚点在点(3,5)的位置。
梯度是上山的方向,那么下山咋办?注意一点,这里的山是连续可微的,那直接沿着上山的方向反着走不就下山了吗?
从数学上看就是直接求出这个梯度向量,然后在它前面乘以 -1 ,然后再沿着这一个方向走,就可以下山去了呀(也就是梯度下降的形象化表示)。
因此再看回来这一幅图:
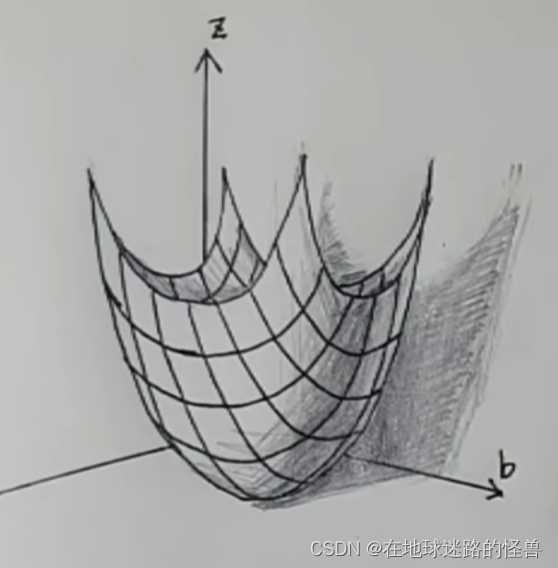
假设当前所在位置在 (Kn,Bn),那么下一个落脚点表示为 (Kn+1,Bn+1),按照我们上面说的,那么 Kn+1 就应该等于 Kn 加上 沿着反梯度的方向也就是减去它的导数,同理 Bn+1 也是一样。那么就可以得到如下式子:

当然别忘记了要在偏导前面乘上一个学习率α控制步长嗷:

最后当这个偏导逐渐为 0 的时候,也就意味着你走不动了,也就来到了最低的位置了。
而此时所得到的 K 值和 B 值呢,就是我们之前线性回归时心心念念的直线的斜率和截距了。
这便是梯度下降算法的第一印象了。