数据结构 —— 并查集
- 并查集
- 并查集实现
- 省份数量
- 并查集的优化
今天我们来了解一下并查集：
并查集
并查集（Disjoint Set Union, DSU）是一种高效的数据结构，用于处理集合的合并（Union）和查询（Find）操作。它的设计目的是快速判断两个元素是否属于同一个集合，并能够将多个集合合并成一个集合。并查集广泛应用于解决一些涉及分类、归属判断的问题，如图的连通性分析、社交网络的朋友圈划分、计算机网络中的域划分等场景。
并查集的核心思想围绕两个基本操作：
-
查找（Find）：确定一个元素所属的集合。这一操作通常伴随着“路径压缩”优化，即在查找的过程中，将沿途经过的所有节点直接连接到它们的根节点，从而加速后续的查找操作。
-
合并（Union）：将两个不同的集合合并成一个集合。为了保持数据结构的高效性，合并时往往采用按秩（每个集合中树的最大深度）或按大小（集合中元素的数量）的启发式合并策略，以避免树的高度过高，保证操作的近似对数时间复杂度。
并查集的典型应用场景包括：
- 连通分量计数：在无向图中快速找出有多少个连通分量。
- 判断连通性：给定两个顶点，判断它们是否在同一个连通分量内。
- 最小生成树算法（如Kruskal算法）中的边的集合判断。
- Tarjan算法中的强连通分量识别。
- 动态集合划分问题，如组织管理、文件系统等。
并查集的魅力在于其简单直观的实现方式和高效的运行效率，尤其是在大数据量下的优秀表现。
并查集的操作其实就是合并两颗树：
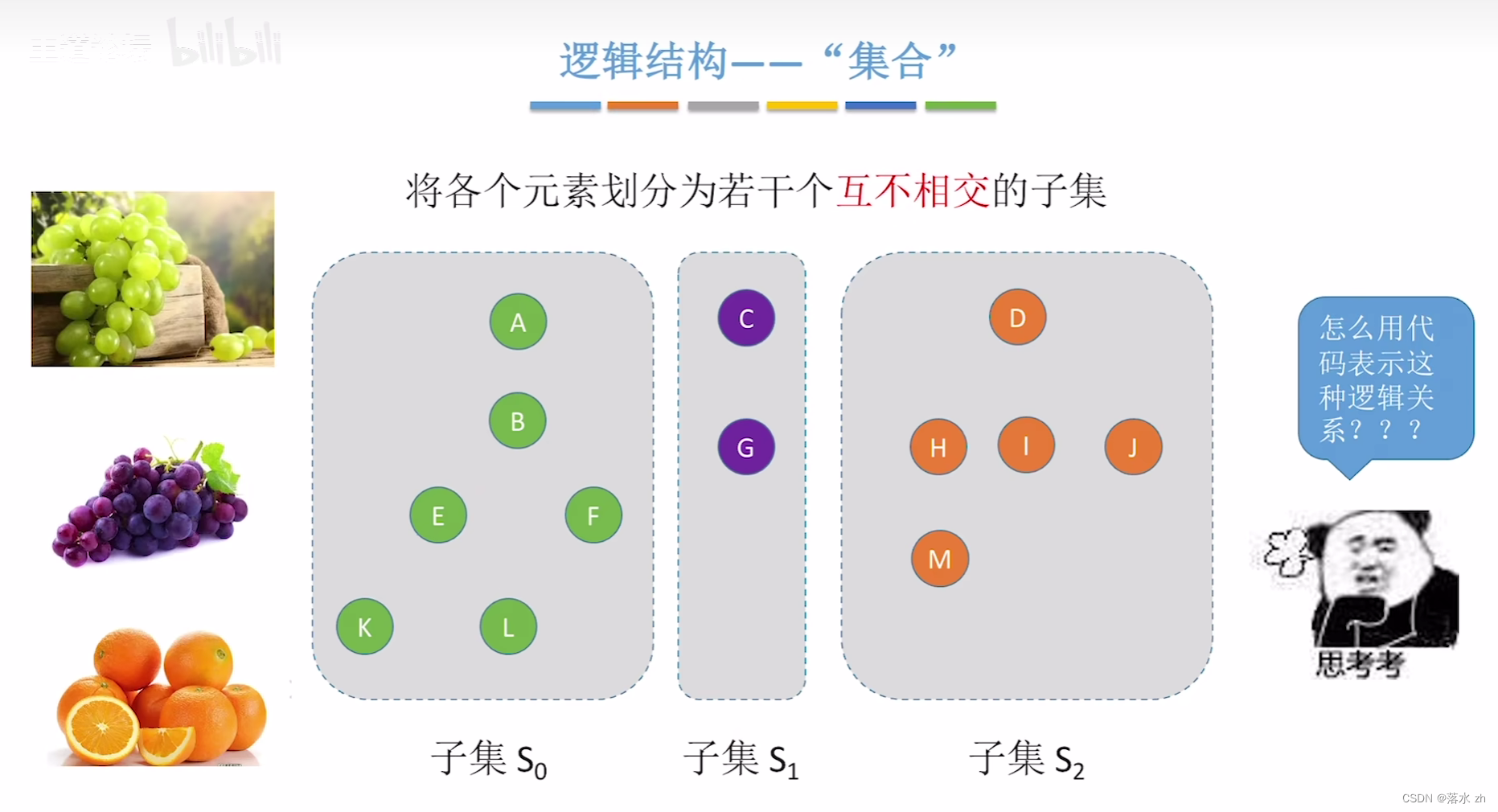
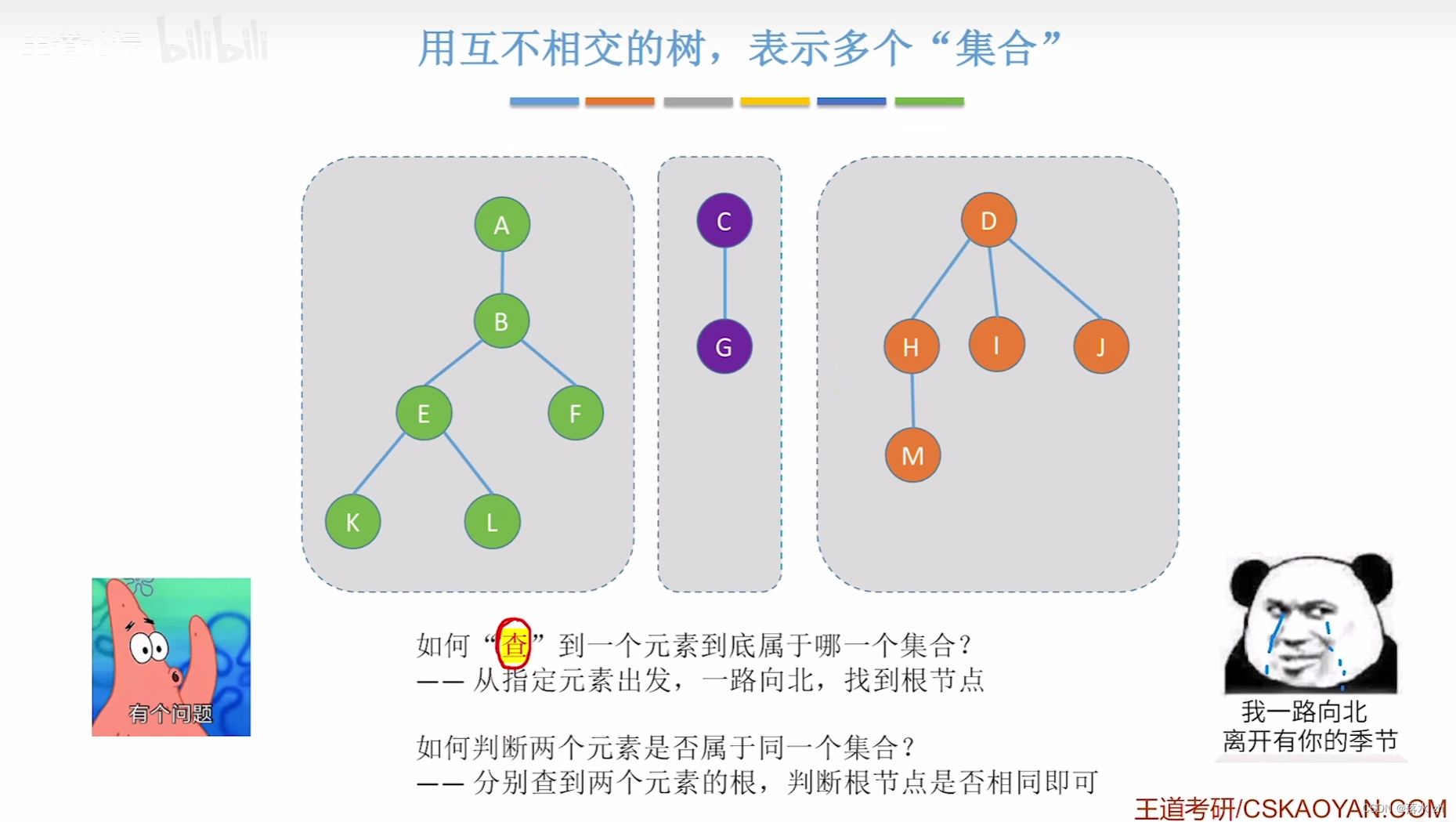同时我们这里可以直接运用数组，数组里面存放指向父亲的父节点：
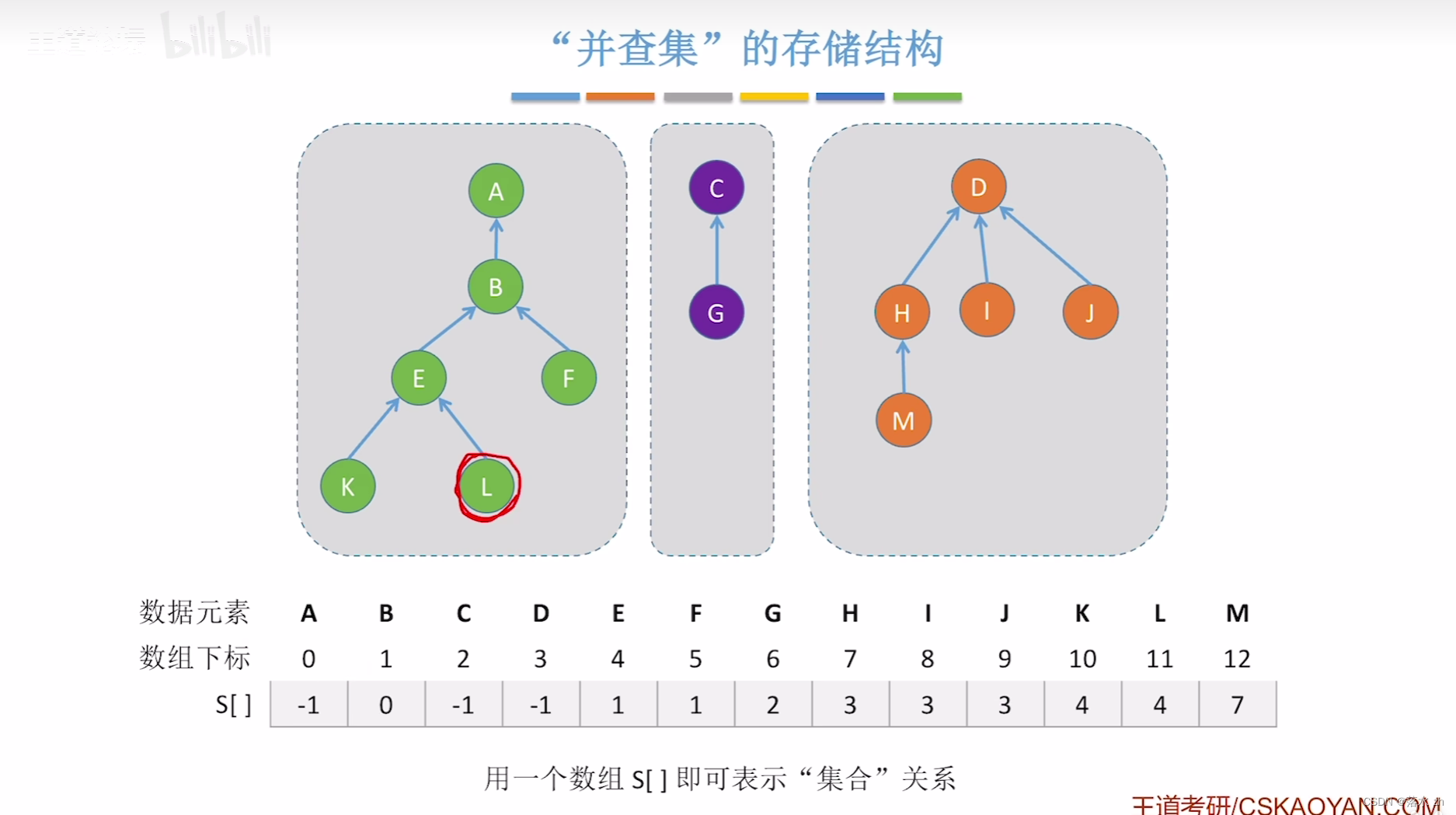
现在我们来实现一个并查集：
并查集实现
我们把架子搭好：
#pragma once
#include<iostream>
#include<vector>
//并查集
class MyUnion
{
public:
//初始化并查集
MyUnion(size_t size)
:_ufs(size,-1)
{
}
//合并
void Union(size_t number1,size_t number2)
{
}
//寻根
int FindRoot(size_t number)
{
}
//判断是否在同一集合
bool InSet(size_t number1,size_t number2)
{
}
//共有几个集合
size_t SetSize()
{
}
private:
std::vector<int> _ufs;
};
我们这里最重要的函数就是要实现寻根，寻根函数是其他函数的基础。
比如我有这样的一个集合：
现在我想把3合并到0那里：
肉眼看其实很简单，就是把3里面的数合并到0处，然后修改3里面的值，改为0（指向0）
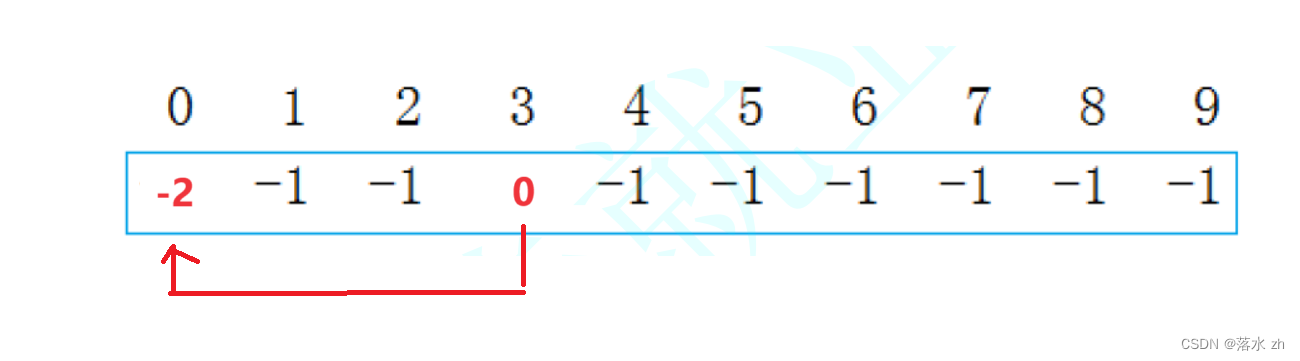
这个时候0这个集合有两个数0,3。我们可以推出几个结论：
- 对应下标里面的数是负数，则这个数为根。
- 对应负数的绝对值表示这个集合里面的元素个数。
这样寻根函数就很好写了，给定一个值，访问对应下标里面的数，若为负数则为根，否则迭代，直到为负数：
//寻根
int FindRoot(size_t number)
{
int root = number;
while(_ufs[root] >= 0)
{
root = _ufs[root];
}
return root;
}
有了寻根函数，合并集合的操作也变的简单：
//合并
void Union(size_t number1,size_t number2)
{
int root1 = FindRoot(number1);
int root2 = FindRoot(number2);
if(root1 == root2)
return;
//这里让大树合并到小树上，树的高度更低，寻根次数会变低
if(root1 < root2)
std::swap(root1,root2);
//父节点个数加上子集合中的个数
_ufs[root1]+=_ufs[root2];
//子节点指向父节点
_ufs[root2] = root1;
}
给出完整代码：
#pragma once
#include<iostream>
#include<vector>
// 并查集类定义
class MyUnion
{
public:
// 构造函数，初始化并查集大小，每个元素初始时属于独立的集合，使用负数表示集合的大小（或作为父节点标记）
MyUnion(size_t size)
:_ufs(size, -1) // _ufs[i] 的值为负数表示 i 是一个集合的根，绝对值表示该集合的元素数量
{
}
// 合并操作，将属于number1和number2的集合合并
void Union(size_t number1, size_t number2)
{
// 分别找到number1和number2的根节点
int root1 = FindRoot(number1);
int root2 = FindRoot(number2);
// 如果根相同，说明已经在同一集合内，无需合并
if(root1 == root2)
return;
// 将较小深度的集合合并到较大深度的集合下，以保持树的平衡（此处通过比较根的值实现）
if(root1 < root2)
std::swap(root1, root2);
// 合并：调整根节点的值以表示集合大小的变化
_ufs[root1] += _ufs[root2];
_ufs[root2] = root1; // 设置root2的父节点为root1
}
// 寻找给定元素的根节点，使用路径压缩优化
int FindRoot(size_t number)
{
int root = number;
// 路径压缩：直接将沿途所有节点指向根节点
while(_ufs[root] >= 0)
{
root = _ufs[root];
}
return root;
}
// 判断两个元素是否属于同一集合
bool InSet(size_t number1, size_t number2)
{
// 通过比较两元素的根节点是否相同来判断
return FindRoot(number1) == FindRoot(number2);
}
// 返回并查集中集合的数量
size_t SetSize()
{
size_t size = 0;
// 遍历数组，负数表示集合的根，因此计数负数的个数即为集合的数量
for(auto e : _ufs)
{
if(e < 0)
size++;
}
return size;
}
// 打印并查集当前状态
void Print()
{
for(auto e : _ufs)
{
std::cout << e << " ";
}
std::cout << std::endl;
}
private:
// 存储并查集数据的向量，_ufs[i]的值如果是负数表示i是集合的根，绝对值表示集合的大小；非负数表示其父节点的索引
std::vector<int> _ufs;
};
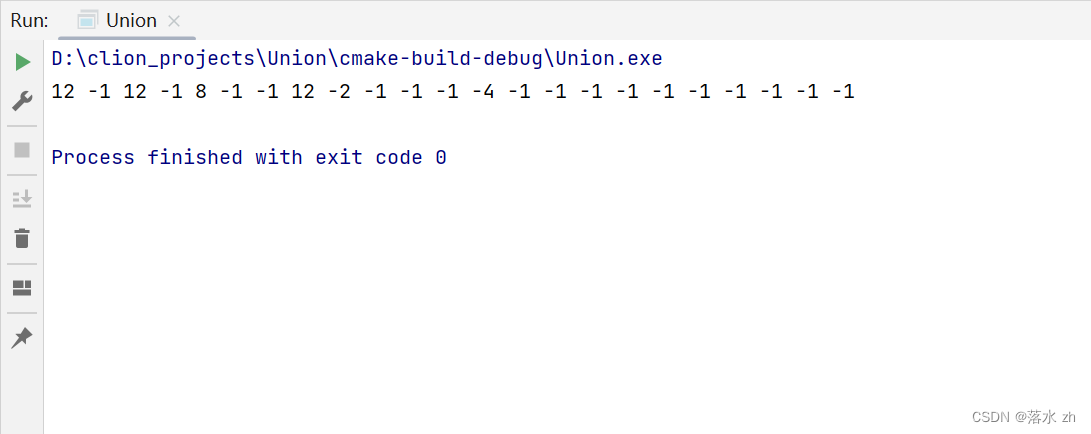
我们来试试：
#include"MyUnion.h"
int main()
{
MyUnion myUnion(23);
myUnion.Union(12,2);
myUnion.Union(12,7);
myUnion.Union(12,0);
myUnion.Union(8,4);
myUnion.Print();
return 0;
}
省份数量
力扣上面也有一道关于并查集的题：
https://leetcode.cn/problems/number-of-provinces/description/
这道题用并查集就很合适：
//并查集
class MyUnion
{
public:
//初始化并查集
MyUnion(int size)
:_ufs(size,-1)
{
}
//合并
void Merege(int number1,int number2)
{
int root1 = FindRoot(number1);
int root2 = FindRoot(number2);
if(root1 == root2)
return;
_ufs[root1]+=_ufs[root2];
_ufs[root2] = root1;
}
//寻根
int FindRoot(int number)
{
int root = number;
while(_ufs[root] >= 0)
{
root = _ufs[root];
}
return root;
}
//判断是否在同一集合
bool InSet(int number1,int number2)
{
return FindRoot(number1) == FindRoot(number2);
}
//共有几个根
size_t SetSize()
{
size_t size = 0;
for(auto e : _ufs)
{
if(e < 0)
size++;
}
return size;
}
private:
vector<int> _ufs;
};
class Solution
{
public:
int findCircleNum(vector<vector<int>>& isConnected)
{
MyUnion myUnion(isConnected.size());
for(int i = 0; i < isConnected.size(); i++)
{
for(int j = 0; j < isConnected[i].size(); j++)
{
if(isConnected[i][j]==1)
{
myUnion.Merege(i,j);
}
}
}
return myUnion.SetSize();
}
};
并查集的优化
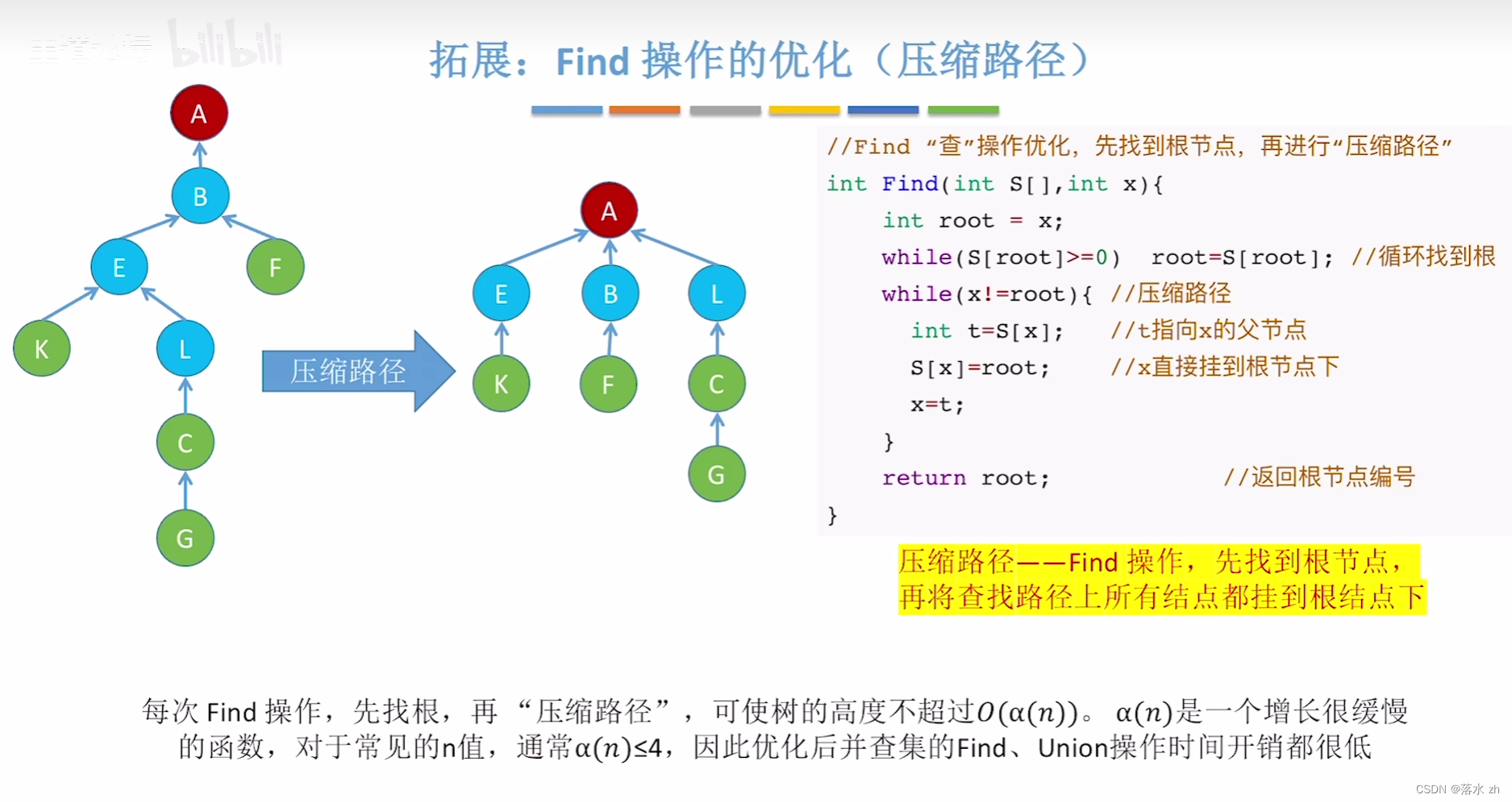
我们这里主要介绍路径压缩：
目的：减少查询路径上的节点数量，使得后续的查询更快。
实现：在执行FindRoot操作时，不仅找到指定节点的根节点，还将沿途的所有节点直接连接到根节点。这样，之后对于这些节点的任何查询都将直接到达根，而无需再次遍历路径。
// 寻根操作，采用路径压缩优化
int FindRoot(size_t number)
{
int root = number;
// 不断迭代直至找到根节点，根节点的.ufs值为负
while(_ufs[root] >= 0)
{
root = _ufs[root]; // 循环直至到达集合的根
}
// 路径压缩：更新从number到根节点这条路径上的所有节点的父节点直接指向根节点
// 这样下次查询这些节点时可以直接跳到根，减少查询时间
while(number != root)
{
// 将当前节点的父节点设置为根节点
int father = _ufs[number]; // 临时存储当前节点的父节点
_ufs[number] = root; // 将当前节点的父节点指向上一步找到的根节点
number = father; // 移动到下一个节点继续进行路径压缩
}
return root; // 最终返回根节点的索引
}
