大家好,我是带我去滑雪!
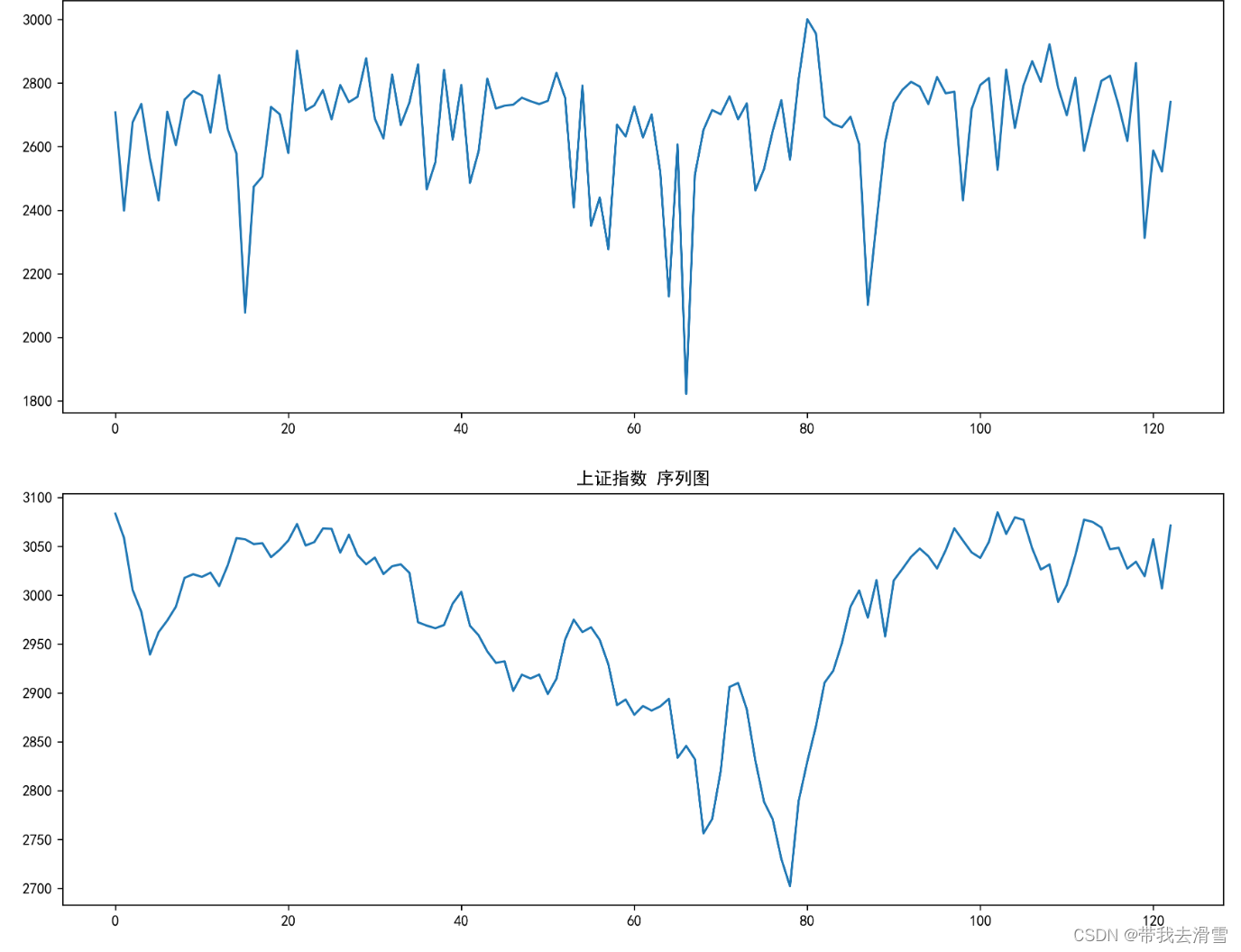
在前一篇文章中,笔者爬取了东方财富网上证指数股吧的495775条评论数据,并对文本进行了情感分析,基于自制的股票情感词典,使用了深度学习模型对爬取的文本数据进行分类标注,将正向文本标注为1,将负向文本标注为-1,将同一天的不同时段的文本标注进行加总,得到该天的情绪指数,而上证指数的收盘价格利用python获取,数据展示如下:
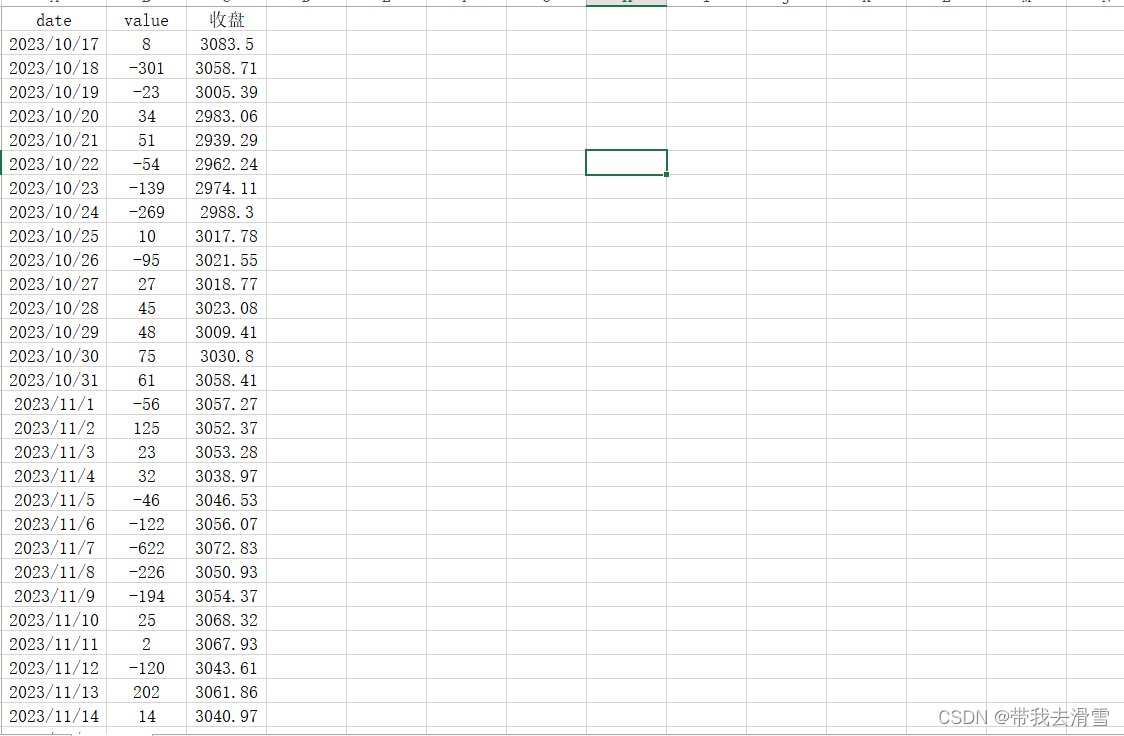
由于情绪指数与上证指数的数值差距较大,后续将情绪指数总体加上2500,使其达到同一水平。下面利用数据构建VAR模型,开始代码实战。
目录
(1)导入模块
(2)导入数据
(3)平稳性检验
(4)差分与协整检验
(5)格兰杰因果检验
(6)VAR模型构建
(7)单位根检验
(8)脉冲响应分析
(1)导入模块
import statsmodels.api as sm
import statsmodels.stats.diagnostic
import matplotlib.pyplot as plt
import pandas as pd
import numpy as np
from statsmodels.tsa.stattools import adfuller as ADF
from statsmodels.tsa.stattools import grangercausalitytests
plt.rcParams ['font.sans-serif'] ='SimHei' #显示中文
plt.rcParams ['axes.unicode_minus']=False (2)导入数据
# 读取数据
train_data = pd.read_csv(r'E:\工作\硕士\博客\博客粉丝问题\情绪指数与上证指数VAR模型\data.csv',encoding="ANSI")
# 确保数据是数值型
train_data['情绪指数'] = pd.to_numeric(train_data['情绪指数'], errors='coerce')
train_data['上证指数'] = pd.to_numeric(train_data['上证指数'], errors='coerce')
# 填补或移除缺失值
train_data.dropna(inplace=True)(3)平稳性检验
def check_station(train_data, column, alpha=0.05):
"""
参数说明:
train_data:原始数据
column:要检验的列
alpha:置信区间,默认为0.05
返回结果:
返回原始数据折线图、平稳性检验结果
"""
data_series = train_data[column]
plt.figure(figsize=(14, 5),dpi=300) # 设置图表大小
plt.plot(data_series)
plt.title(f'{column} 序列图')
print("*如数据围绕某一常数上下波动,没有上升或下降的趋势,即可认为是平稳序列。")
data_adf = ADF(data_series) # 单位根检验,及特征根检验,序列平稳,就不存在单位根,检验结果的P值越小越好
if data_adf[1] < alpha:
result = f"{column} 序列是弱平稳序列,P值为:{round(float(data_adf[1]), 4)}"
else:
result = f"{column} 序列不是弱平稳序列,P值为:{round(float(data_adf[1]), 4)}"
return result
# 对每个列进行平稳性检查
for column in train_data.columns:
result = check_station(train_data, column)
print(result)
输出结果:
*如数据围绕某一常数上下波动,没有上升或下降的趋势,即可认为是平稳序列。
情绪指数 序列是弱平稳序列,P值为:0.0
*如数据围绕某一常数上下波动,没有上升或下降的趋势,即可认为是平稳序列。
上证指数 序列不是弱平稳序列,P值为:0.3602
(4)差分与协整检验
def coint_pvalue_matrix(train_data):
"""
参数说明:
train_data:原始数据,为dataframe格式,每一列代表一个变量:
返回结果:
返回协整检验的p_value,p_value越低,越显著。
"""
train_data=train_data
n=len(train_data.columns)
#创建一个空的矩阵
coint_pvalue=np.ones((n,n))
#将矩阵转换为dataframe格式
coint_pvalue=pd.DataFrame(coint_pvalue)
coint_pvalue.index=train_data.columns
coint_pvalue.columns=train_data.columns
for column_1 in train_data.columns:
for column_2 in train_data.columns:
#协整检验会返回三个值,第二值为p值,p值越小,说明存在长期协整关系
if column_1!=column_2:
result = sm.tsa.stattools.coint(train_data[column_1],train_data[column_2])
coint_pvalue.loc[column_1,column_2]=round(result[1],4)#pd.loc[index,column]
return coint_pvalue
coint_pvalue=coint_pvalue_matrix(train_data)
print(coint_pvalue)#由于序列上证指数序列不平稳,需要差分,且不存在长期协整关系(5)格兰杰因果检验
#差分后序列平稳,进行格兰杰因果检验
def granger_pvalue_matrix(train_data,test="ssr_chi2test",lags=10):
"""
参数说明:
train_data:原始数据,为dataframe格式,每一列代表一个变量:第一列为Y,第二列为X,检验X是否为Y的格兰杰原因:
lags:为最大滞后阶数
test:格兰杰检验方法,一共会有4个p值,默认选用ssr_chi2test的p值(其他可选项lrtest,params_ftest,ssr_ftest)
返回结果:
返回格兰杰检验的p_value,p_value越低,越显著。说明X是Y的格兰杰原因。
"""
train_data=train_data
n=len(train_data.columns)
#初始化一个dataframe格式
granger_pvalue=pd.DataFrame(np.zeros((n,n)))
granger_pvalue.index=train_data.columns
granger_pvalue.columns=train_data.columns
for column_1 in granger_pvalue.index:
for column_2 in granger_pvalue.columns:
result = grangercausalitytests(train_data[[column_1,column_2]],maxlag=lags,verbose=False)#verbose=False不打印结果
p_values = [round(result[i+1][0][test][1],4) for i in range(lags)]
min_p_value = np.min(p_values)#一共滞后10阶,没滞后1阶都会有一个p值,获取最小的那个p值
granger_pvalue.loc[column_1,column_2]=min_p_value
granger_pvalue.columns = [column_2 + '_x' for column_2 in granger_pvalue.columns]
granger_pvalue.index = [column_1 + '_y' for column_1 in granger_pvalue.index]
return granger_pvalue
granger_pvalue=granger_pvalue_matrix(train_data)
print(granger_pvalue)(6)VAR模型构建
#VAR模型滞后阶数不方便单独通过图表判断,一般都是设置一个最大滞后项,然后运用AIC信息准则的方式来判断,AIC值越小,模型拟合越优。
model = sm.tsa.VAR(train_data)
result=model.fit(maxlags=10, method='ols', ic="aic", trend='c', verbose=False)#ic="aic"系统会根据aic准则在(1-10)中自动选取最优模型
print(result.summary())输出结果:
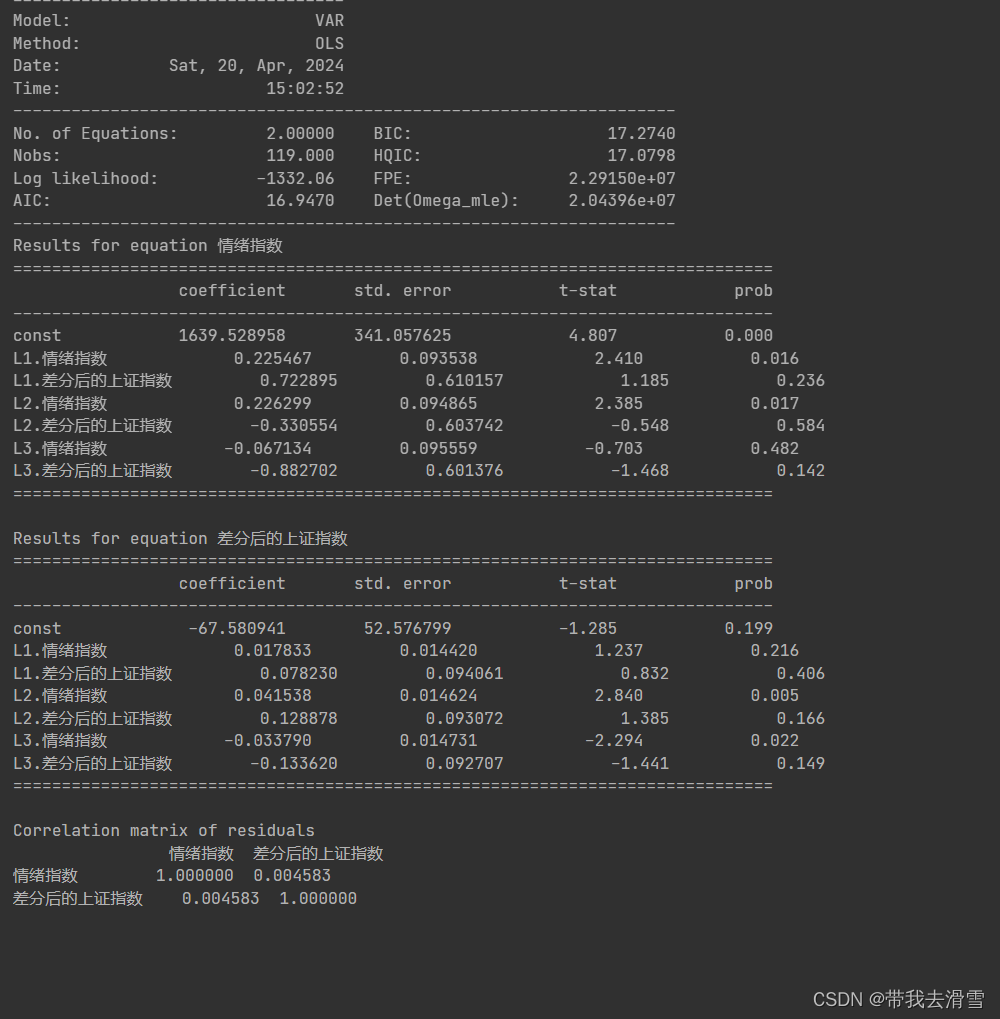
(7)单位根检验
def root_ar(roots,maxlim=1.5):
"""
参数说明:
roots:VAR模型返回的模型根。
maxlim:坐标轴的最大值
返回结果:
AR根图,如果根都在单位圆内,则为平稳模型。
"""
#绘制单位圆
x=np.linspace(-1,1,400)
y=np.linspace(-1,1,400)
[X,Y]=np.meshgrid(x,y)
Z=X*X+Y*Y
plt.figure(figsize=(5,5))
plt.contour(X,Y,Z,1)
plt.title("Inverse Roots of AR")
#提取模型根的实部和虚部
roots_real=roots.real
roots_imag=roots.imag
plt.xlim(-maxlim,maxlim)
plt.ylim(-maxlim,maxlim)
#画中间十字线
h_x=np.linspace(0,0,400)
h_y=np.linspace(-maxlim,maxlim,400)
plt.plot(h_y,h_x,"b--")
plt.plot(h_x,h_y,"b--")
"""
VAR模型库,对roots的解释如下:
The roots of the VAR process are the solution to (I - coefs[0]*z - coefs[1]*z**2 … - coefs[p-1]*z**k_ar) = 0.
Note that the inverse roots are returned,
and stability requires that the roots lie outside the unit circle.
根在模型外说明模型是平稳的,这和传统的AR根图画法有很大不同;
因此我们将其根转换成其倒数,这样根就会落在单位圆内。
"""
#将根转化成根的倒数(根为复数)
Inverse_real=roots_real/(np.abs(roots)*np.abs(roots))#abs即可以算绝对值,也可以算复数的模
Inverse_imag=-roots_imag/(np.abs(roots)*np.abs(roots))
plt.plot(Inverse_real,Inverse_imag,"ro")
plt.savefig(r'E:\工作\硕士\博客\博客粉丝问题\接单34-1200元\情绪指数与上证指数VAR模型\AR单位根检验.png',
bbox_inches ="tight",
pad_inches = 1,
transparent = True,
facecolor ="w",
edgecolor ='w',
dpi=300,
orientation ='landscape')
return None
roots=result.roots
root_ar(roots,maxlim=1.5)
#从AR根图来看,所有根都落在单位圆内,因此我们认为模型是平稳的。输出结果:
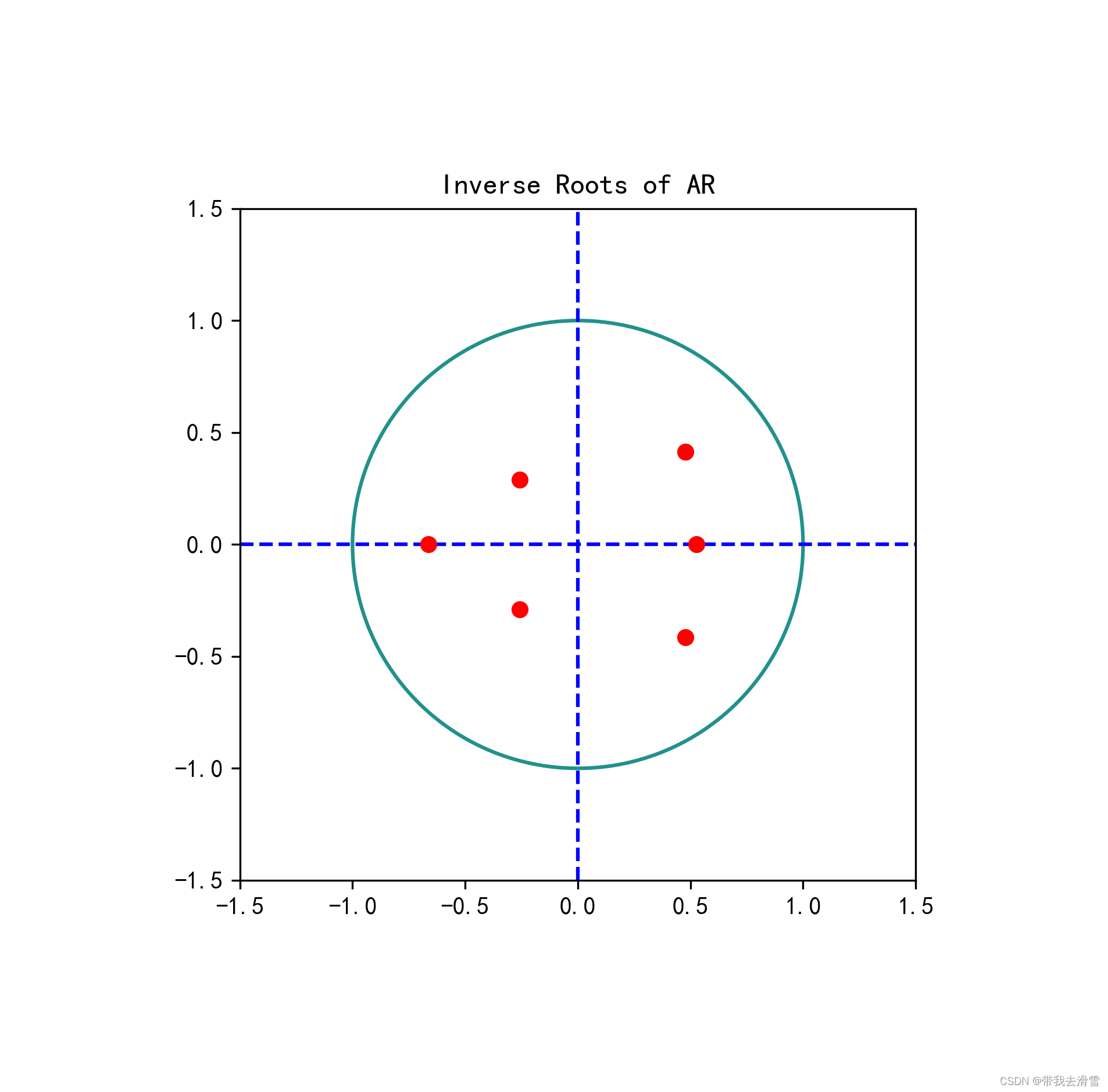
说明模型是有效的。
(8)脉冲响应分析
#绘制脉冲响应图
irf = result.irf(15)
irf.plot(orth=False)
plt.savefig(r'E:\工作\硕士\博客\博客粉丝问题\情绪指数与上证指数VAR模型\脉冲响应图.png',
bbox_inches ="tight",
pad_inches = 1,
transparent = True,
facecolor ="w",
edgecolor ='w',
dpi=300,
orientation ='landscape')输出结果:
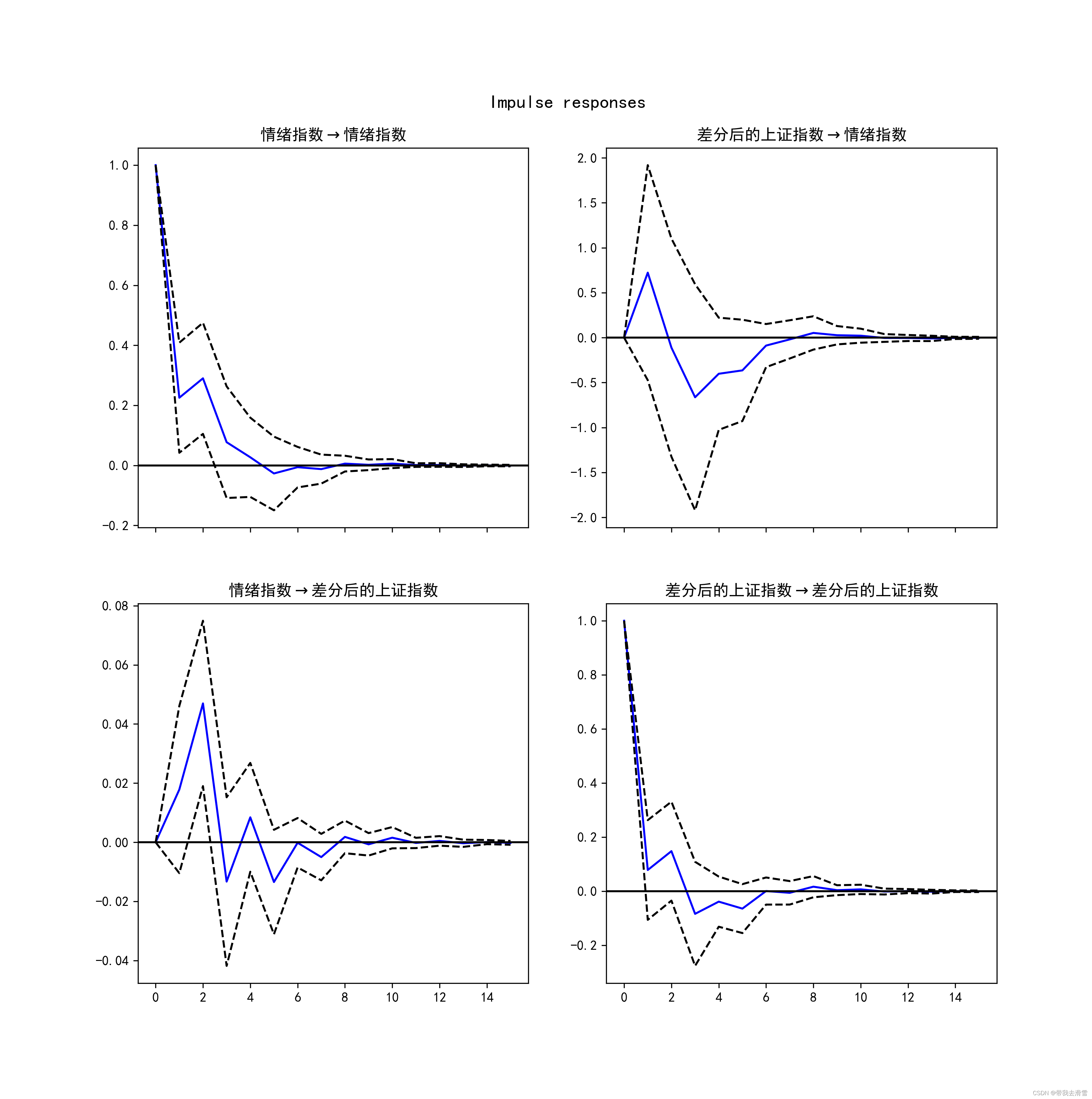
需要数据集的家人们可以去百度网盘(永久有效)获取:
链接:
提取码:2138
更多优质内容持续发布中,请移步主页查看。
点赞+关注,下次不迷路!