Python27 神经网络中的重要概念和可视化实现

1. 神经网络背后的直观知识

神经网络的工作方式非常相似：它接受多个输入，经过多个隐藏层中的多个神经元进行处理，并通过输出层返回结果，这个过程在技术上称为“前向传播”。

接下来，将神经网络的输出与实际输出进行比较。任务是使神经网络的输出尽可能接近实际（期望的）输出。在这个过程中，每个神经元都会产生一些误差，开发人员目标是最小化这些误差。

为了减少误差，尝试调整神经元的值和权重，特别是那些对错误“贡献”更多的神经元。这个过程称为“反向传播”。

为了有效地最小化误差并减少迭代次数，神经网络通常使用梯度下降等优化算法。

2. 多层感知器及其基础知识

就像原子是形成地球上任何物质的基础 - 神经网络的基本形成单位是感知器。那么，什么是感知器呢？感知器可以被理解为需要多个输入并产生一个输出的任何东西。例如，看下面的图片：

上述结构需要三个输入并产生一个输出，下一个逻辑问题是输入和输出之间的关系是什么？从基本的方式着手，寻求更复杂的方法。

下面讨论三种创建输入输出关系的方法：

通过直接组合输入和计算基于阈值的输出。例如：取x1 = 0，x2 = 1，x3 = 1并设置阈值= 0。因此，如果x1 + x2 + x3> 0，则输出为1，否则为0。可以看出，在这种情况下，感知器会将输出计算为1。
接下来为输入添加权重。例如，分别为x1，x2和x3分配w1 = 2，w2 = 3和w3 = 4。为了计算输出，将输入与相应权重相乘，并将其与阈值进行比较，如w1 * x1 + w2 * x2 + w3 * x3>阈值。与x1和x2相比，这些权重对于x3显得更重要。
最后添加偏置量：每个感知器也有一个偏置量，可以被认为是感知器为什么灵活。它与某种线性函数y = ax + b的常数b类似，它允许上下移动线以适应数据更好的预测。假设没有b，线将始终通过原点（0，0），并且可能会得到较差的拟合。例如，感知器可以具有两个输入，在这种情况下，它需要三个权重。每个输入一个，偏置一个。现在输入的线性表示将如下所示：w1 * x1 + w2 * x2 + w3 * x3 + 1 * b。

但是，上面所讲的感知器之间的关系都是线性的，所以人们将感知器演化成现在所谓的人造神经元，对于输入和偏差，神经元将使用非线性变换（激活函数）。

3. 什么是激活函数？

激活函数将加权输入（w1 * x1 + w2 * x2 + w3 * x3 + 1 * b）的和作为参数，并返回神经元的输出。

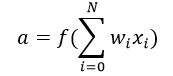
在上式中，用x0表示1，w0表示b。

激活函数主要用于进行非线性变换，它能够拟合非线性假设或估计复杂函数，有多种激活功能，如：“Sigmoid”，“Tanh”，ReLu等等。

4. 前向传播，反向传播和训练次数(epochs)

到目前为止，神经网络已经计算了输出，这个过程被称为“正向传播”。但是如果估计的输出远离实际输出（非常大的误差）怎么办？基于错误更新偏差和权重。这种权重和偏差更新过程被称为“反向传播”。

反向传播（BP）算法通过确定输出处的损耗（或误差），然后将其传播回网络来工作，更新权重以最小化每个神经元产生的错误。最小化误差的第一步是确定每个节点w.r.t.的梯度（Derivatives），最终实现输出。

这一轮的前向和后向传播迭代被称为一个训练迭代也称为“Epoch”。

ps:e（一）poch（波）的意思;一个epoch是指把所有训练数据完整的过一遍

5. 多层感知器

关于多层感知器。到目前为止，已经看到只有一个由3个输入节点组成的单层，即x1，x2和x3，以及由单个神经元组成的输出层。但是，出于实际，单层网络只能做到这一点。如下所示，MLP由层叠在输入层和输出层之间的许多隐层组成。

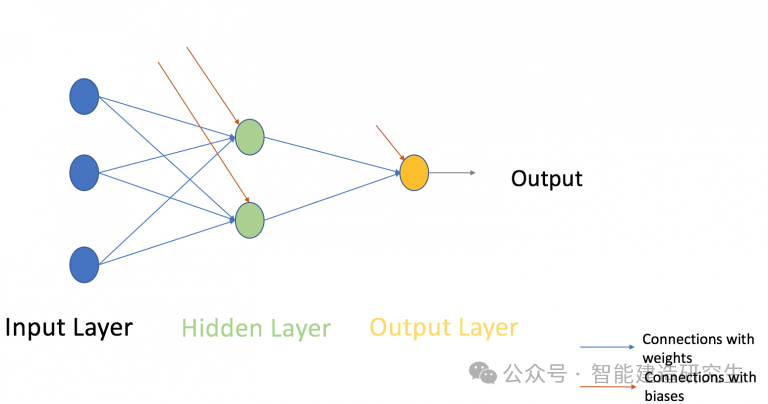
多层感知器

上面的图像只显示一个单一的隐藏层，但实际上可以包含多个隐藏层。在MLP的情况下要记住的另一点是，所有层都完全连接，即层中的每个节点（输入和输出层除外）连接到上一层和下一层中的每个节点。继续下一个主题，即神经网络的训练算法（最小化误差)。在这里，我们将看到最常见的训练算法称为梯度下降。

6. 全批量梯度下降和随机梯度下降

Gradient Descent的第二个变体通过使用相同的更新算法执行更新MLP的权重的相同工作，但差异在于用于更新权重和偏差的训练样本的数量。

全部批量梯度下降算法作为名称意味着使用所有的训练数据点来更新每个权重一次，而随机渐变使用1个或更多（样本），但从不使整个训练数据更新权重一次。

用一个简单的例子来理解这个10个数据点的数据集，它们有两个权重w1和w2。

全批：可以使用10个数据点（整个训练数据），并计算w1（Δw1）的变化和w2（Δw2）的变化，并更新w1和w2。
SGD：使用第一个数据点并计算w1（Δw1）的变化，并改变w2（Δw2），同时更新w1和w2。接下来，当使用第二个数据点时，将处理更新的权重。

7. 神经网络方法的步骤

多层感知器

接下来是一步一步地构建神经网络的方法（MLP与一个隐藏层，类似于上图所示的架构）。在输出层只有一个神经元，因为要解决二进制分类问题（预测0或1)。

一般步骤：

输入和输出
- X作为输入矩阵
- y作为输出矩阵
用随机值初始化权重和偏差（这是一次启动，在下一次迭代中，将使用更新的权重和偏差）。定义：
- wh作为权重矩阵隐藏层
- bh作为隐藏层的偏置矩阵
- wout作为输出层的权重矩阵
- bout作为偏置矩阵作为输出层
将输入和权重的矩阵点积分配给输入和隐藏层之间的边，然后将隐层神经元的偏差添加到相应的输入，这被称为线性变换：

hidden_layer_input= matrix_dot_product(X,wh) + bh
使用激活函数（Sigmoid）执行非线性变换。Sigmoid将返回输出1/(1 + exp(-x)).hiddenlayer_activations = sigmoid(hidden_layer_input)
对隐藏层激活进行线性变换（取矩阵点积，并加上输出层神经元的偏差），然后应用激活函数（再次使用Sigmoid，但是根据您的任务可以使用任何其他激活函数）来预测输出

output_layer_input = matrix_dot_product (hiddenlayer_activations * wout ) + bout

output = sigmoid(output_layer_input)

所有上述步骤被称为“前向传播”（Forward Propagation）

将预测与实际输出进行比较，并计算误差梯度（实际预测值）。误差是均方损失= ((Y-t)^2)/2E = y – output
计算隐藏和输出层神经元的斜率/斜率（为了计算斜率，我们计算每个神经元的每层的非线性激活x的导数）。S形梯度可以返回 x * (1 – x).

slope_output_layer = derivatives_sigmoid(output)

slope_hidden_layer = derivatives_sigmoid(hiddenlayer_activations)
计算输出层的变化因子（delta），取决于误差梯度乘以输出层激活的斜率d_output = E * slope_output_layer
在这一步，错误将传播回网络，这意味着隐藏层的错误。为此，我们将采用输出层三角形的点积与隐藏层和输出层之间的边缘的重量参数（wout.T）。Error_at_hidden_layer = matrix_dot_product(d_output, wout.Transpose)
计算隐层的变化因子（delta），将隐层的误差乘以隐藏层激活的斜率d_hiddenlayer = Error_at_hidden_layer * slope_hidden_layer
在输出和隐藏层更新权重：网络中的权重可以从为训练示例计算的错误中更新。wout = wout + matrix_dot_product(hiddenlayer_activations.Transpose, d_output)*learning_rate

wh = wh + matrix_dot_product(X.Transpose,d_hiddenlayer)*learning_ratelearning_rate：权重更新的量由称为学习率的配置参数控制）
在输出和隐藏层更新偏差：网络中的偏差可以从该神经元的聚合错误中更新。

bh = bh + sum(d_hiddenlayer, axis=0) * learning_rate

bout = bout + sum(d_output, axis=0)*learning_rate
- bias at output_layer =bias at output_layer + sum of delta of output_layer at row-wise * learning_rate
- bias at hidden_layer =bias at hidden_layer + sum of delta of output_layer at row-wise * learning_rate

从6到12的步骤被称为“向后传播”(Backward Propagation)

一个正向和反向传播迭代被认为是一个训练周期。以上，我们更新了隐藏和输出层的权重和偏差，并使用了全批量梯度下降算法。

8. 神经网络方法的可视化步骤

重复上述步骤，可视化输入，权重，偏差，输出，误差矩阵，以了解神经网络（MLP）的工作方法。

注意：
- 对于良好的可视化图像，我有2或3个位置的十进制小数位。
- 黄色填充的细胞代表当前活动细胞
- 橙色单元格表示用于填充当前单元格值的输入
步骤1：读取输入和输出
步骤2：用随机值初始化权重和偏差（有初始化权重和偏差的方法，但是现在用随机值初始化）
步骤3：计算隐层输入：
hidden_layer_input= matrix_dot_product(X,wh) + bh
步骤4：对隐藏的线性输入进行非线性变换
hiddenlayer_activations = sigmoid(hidden_layer_input)
步骤5：在输出层执行隐层激活的线性和非线性变换
output_layer_input = matrix_dot_product (hiddenlayer_activations * wout ) + bout
output = sigmoid(output_layer_input)
步骤6：计算输出层的误差（E）梯度
E = y-output
步骤7：计算输出和隐藏层的斜率
Slope_output_layer= derivatives_sigmoid(output)
Slope_hidden_layer = derivatives_sigmoid(hiddenlayer_activations)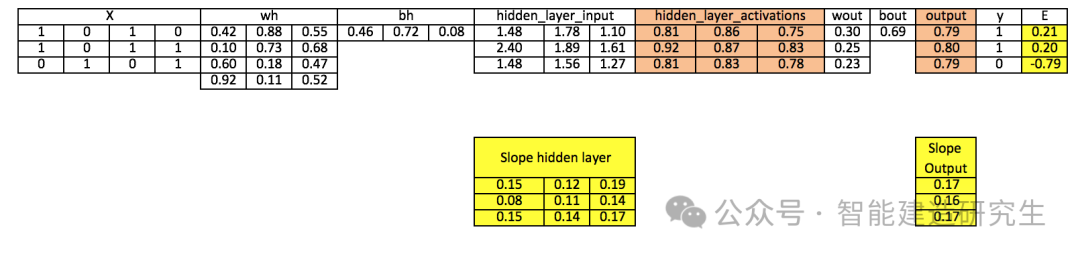
步骤8：计算输出层的增量
d_output = E * slope_output_layer*lr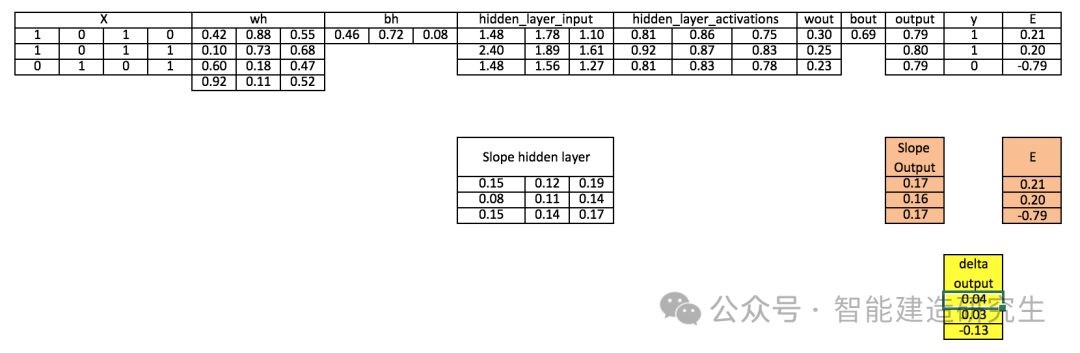
步骤9：计算隐藏层的误差
Error_at_hidden_layer = matrix_dot_product(d_output, wout.Transpose)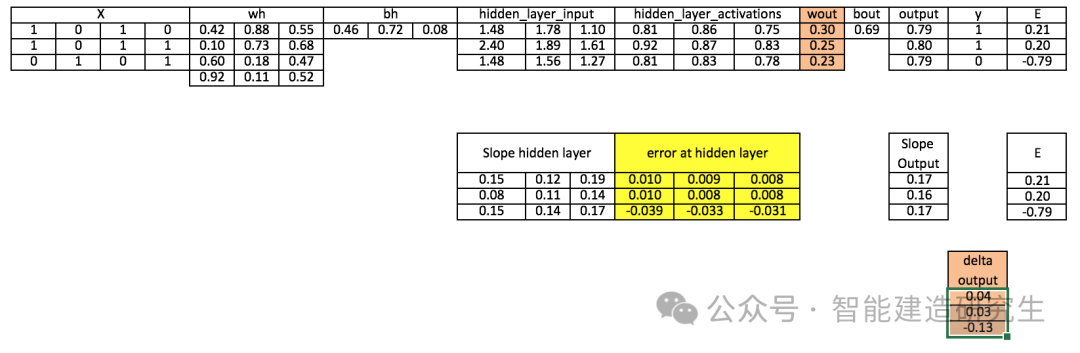
步骤10：计算隐藏层的增量
d_hiddenlayer = Error_at_hidden_layer * slope_hidden_layer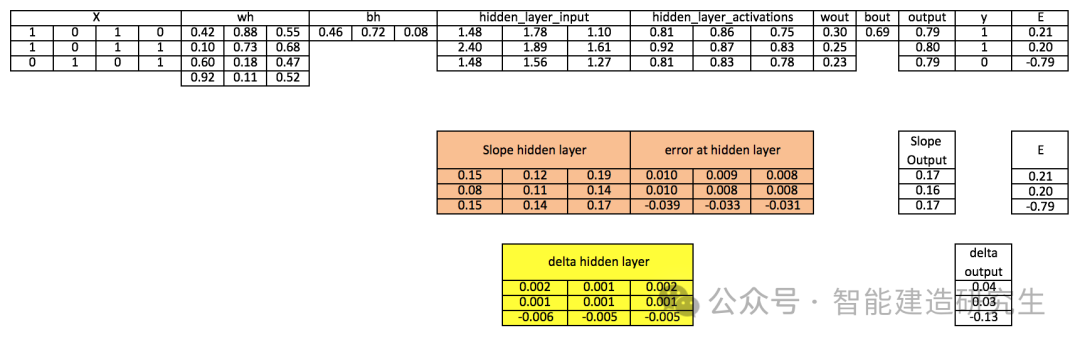
步骤11：更新输出和隐藏层的权重
wout = wout + matrix_dot_product(hiddenlayer_activations.Transpose, d_output)*learning_rate
wh = wh+ matrix_dot_product(X.Transpose,d_hiddenlayer)*learning_rate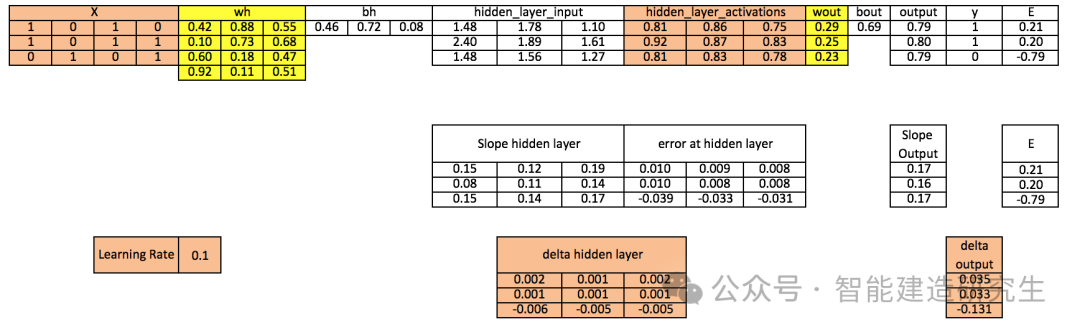
步骤12：更新输出和隐藏层的偏置量
bh = bh + sum(d_hiddenlayer, axis=0) * learning_rate
bout = bout + sum(d_output, axis=0)*learning_rate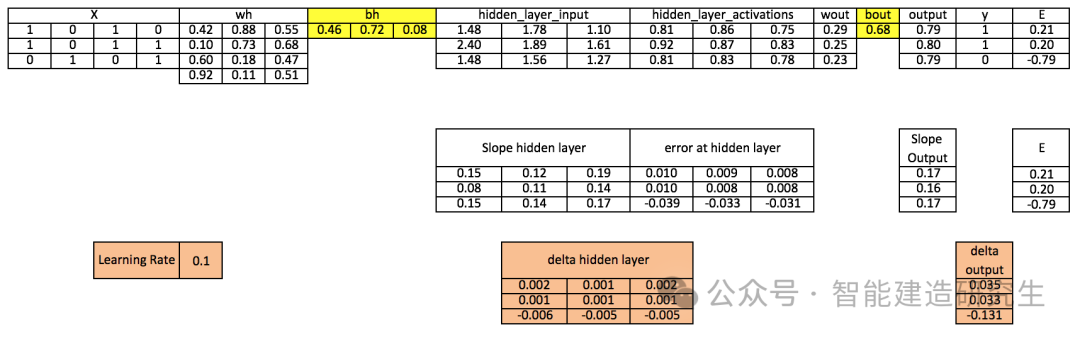

以上，可以看到仍然有一个很好的误差而不接近于实际目标值，因为神经网络已经完成了一次训练迭代。如果多次训练模型，那么这将非常接近的实际结果。完成数千次迭代后的结果接近实际的目标值（[[0.98032096] [0.96845624] [0.04532167]]）。

9.使用Numpy（Python）实现NN

import numpy as np

# Input array
X=np.array([[1,0,1,0],[1,0,1,1],[0,1,0,1]])

# Output
y=np.array([[1],[1],[0]])

# Sigmoid Function
def sigmoid (x):
    return 1/(1 + np.exp(-x))

# Derivative of Sigmoid Function
def derivatives_sigmoid(x):
    return x * (1 - x)

# Variable initialization
epoch=5000 #Setting training iterations
lr=0.1  # Setting learning rate
inputlayer_neurons = X.shape[1]  # number of features in data set
hiddenlayer_neurons = 3  # number of hidden layers neurons
output_neurons = 1  # number of neurons at output layer

# weight and bias initialization
wh=np.random.uniform(size=(inputlayer_neurons,hiddenlayer_neurons))
bh=np.random.uniform(size=(1,hiddenlayer_neurons))
wout=np.random.uniform(size=(hiddenlayer_neurons,output_neurons))
bout=np.random.uniform(size=(1,output_neurons))

for i in range(epoch):
    # Forward Propogation
    hidden_layer_input1=np.dot(X,wh)
    hidden_layer_input=hidden_layer_input1 + bh
    hiddenlayer_activations = sigmoid(hidden_layer_input)
    output_layer_input1=np.dot(hiddenlayer_activations,wout)
    output_layer_input= output_layer_input1+ bout
    output = sigmoid(output_layer_input)
    # Backpropagation
    E = y-output
    slope_output_layer = derivatives_sigmoid(output)
    slope_hidden_layer = derivatives_sigmoid(hiddenlayer_activations)
    d_output = E * slope_output_layer
    Error_at_hidden_layer = d_output.dot(wout.T)
    d_hiddenlayer = Error_at_hidden_layer * slope_hidden_layer
    wout += hiddenlayer_activations.T.dot(d_output) *lr
    bout += np.sum(d_output, axis=0,keepdims=True) *lr
    wh += X.T.dot(d_hiddenlayer) *lr
    bh += np.sum(d_hiddenlayer, axis=0,keepdims=True) *lr

print("output of Forward Propogation:\n{}".format(output))
print("wout,bout of Backpropagation:\n{},\n{}".format(wout,bout))

# 输出：
'''
output of Forward Propogation:
[[0.98029862]
 [0.97141123]
 [0.03712863]]
wout,bout of Backpropagation:
[[-3.67752007]
 [ 4.10817642]
 [ 0.70303165]],
[[-0.48310214]]
'''

原文参见：https://www.analyticsvidhya.com/blog/2020/07/neural-networks-from-scratch-in-python-and-r/

以上内容总结自网络，如有帮助欢迎转发，我们下次再见！