目录
一、向量和矩阵的范数运算
二、矩阵的秩
三、矩阵的行列式
四、矩阵的迹
五、矩阵的化零矩阵
六、矩阵的正交空间
七、矩阵的约化行阶梯形式
八、矩阵空间之间的夹角
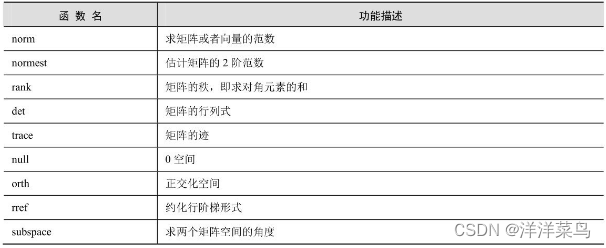
MATLAB 提供的矩阵分析函数:
一、向量和矩阵的范数运算
(1)在MATLAB中,求向量范数的函数具体用法如下:
- N=norm(x,p):对任意大于1的p值,返回向量x的p阶范数。
- N=norm(x):返回向量的2阶范数,相当于N=norm(x,2)。
- N=norm(x,inf):返回向量的∞阶范数,相当于N=max(abs(x))。
- N=norm(x,-inf):返回向量的-∞阶范数,相当于N=min(abs(x))。
(2)在MATLAB中,求矩阵范数的函数具体用法如下:
- N=norm(A) :计算矩阵的2阶范数,也就是最大奇异值。
- N=norm(A,p) :根据参数p的值不同,求不同阶的范数值。当p=1时,计算矩阵A的1阶范数,相当于max(sum(abs(A)))。当p=2时,计算矩阵A的2阶范数,相当于norm(A)。当p=inf时,计算矩阵A 的∞阶范数,相当于max(sum(abs(A')))。当p=pro时,计算矩阵A的F范数(Frobenius范数),相当于sqrt(sum(diag(A'*A)))。
示例1:求向量x的2 阶范数
norm(1:6,2)运行结果:
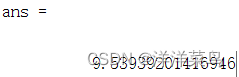
注意:当矩阵维数比较大时,会导致计算矩阵范数的时间比较长,并且当一个近似的范数值满足要求时,可以考虑使用函数normest()来估计2阶范数值。函数normest()最初开发时是为了提供给稀疏矩阵使用的,同时它也能接收满矩阵的输入,一般在满矩阵维数比较大时使用。
(3)函数normest()的用法如下:
- normest(S):估计矩阵S 的2 阶范数值。
- normest(S,tol):使用to作为允许的相对误差。
示例2:求矩阵的范式
A=[1 2 3;3 4 5;7 8 9];
B=norm(A,1); %矩阵的1阶范式
C=norm(A); %矩阵的2阶范式
D=norm(A,inf); %矩阵的无穷范式
E=norm(A,'fro'); %矩阵的Frobenius范式
F=normest(A); %矩阵的2阶范式的估计值
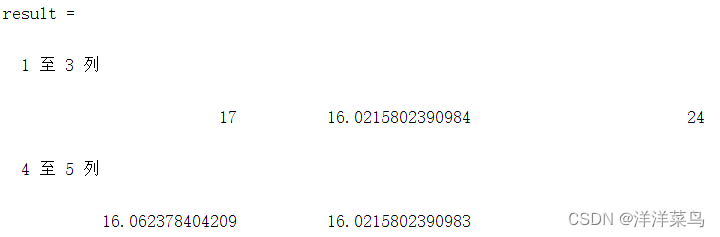
result=[B C D E F]运行结果:
二、矩阵的秩
矩阵A中线性无关的列向量个数称为列秩,线性无关的行向量个数称为行秩。MATLAB中用函数rank()来计算矩阵的秩。函数rank()的用法如下:
- rank(A):用默认允许误差计算矩阵的秩。
- rank(A,tol):给定允许误差计算矩阵的秩,to=max(size(A))·eps(norm(A))。
示例3:求矩阵的秩
A=[1 2 3;3 4 5;7 8 9];
B=magic(3);
C=rank(A) %矩阵的秩
D=rank(B)运行结果:
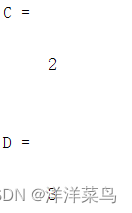
三、矩阵的行列式
在MATLAB 中用函数 det()来计算矩阵的行列式。
示例4:计算矩阵的行列式
A=[1 2 3;3 4 5;7 8 9];
B=magic(3);
C=det(A) %矩阵的行列式
D=det(B)运行结果:

四、矩阵的迹
矩阵的迹定义为矩阵对角元素之和。在MATLAB中用函数trace()来计算矩阵的迹。
示例5:矩阵的迹计算
A=[1 2 3;3 4 5;7 8 9];
B=magic(3);
C=trace(A) %矩阵的迹
D=trace(B)运行结果:
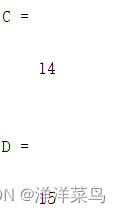
五、矩阵的化零矩阵
MATLAB中提供了求化零矩阵的函数null()。其用法如下:
- Z = null(A):返回矩阵A 的一个化零矩阵,如果化零矩阵不存在则返回空矩阵。
- Z = null(A,'r'):返回有理数形式的化零矩阵。
示例6:求矩阵的化零矩阵
A=[1 2 3;3 4 5;7 8 9];
B=null(A) %求矩阵A的化零矩阵
C=A*B
D=null(A,'r') %求矩阵A的有理数形式的化零矩阵
E=A*D运行结果:

六、矩阵的正交空间
矩阵A的正交空间Q具有Q'·Q=I的性质,并且Q的列矢量构成的线性空间与矩阵A的列矢量构成的线性空间相同,且正交空间Q与矩阵A具有相同的秩。MATLAB中提供了函数orth()来求正交空间Q。
示例7:矩阵的正交空间求解
A=[1 2 3;3 4 5;7 8 9];
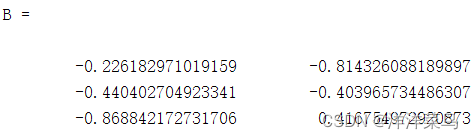
B=orth(A) %求矩阵A的正交空间运行结果:
七、矩阵的约化行阶梯形式
矩阵的约化行阶梯形式是高斯-约旦消去法解线性方程组的结果,其形式为:

MATLAB中提供了函数rref()来求矩阵的约化行阶梯形式。其用法如下:
- R = rref(A):返回矩阵A的约化行阶梯形式R。
- [R,jb]=rref(A):返回矩阵A的约化行阶梯形式R,并返回1×r的向量jb,r为矩阵A的秩;A(:,jb)是矩阵A的列矢量构成的线性空间;R(1:r,jb)是r×r 的单位矩阵。
- [R,jb] = rref(A,tol):以to作为允许的相对误差计算矩阵A 的秩。
示例8:求矩阵A的约化行阶梯形式
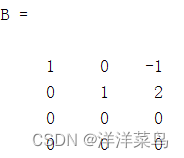
A=[1 2 3;3 4 5;7 8 9;10 11 12];
B=rref(A) %求矩阵A的约化行阶梯形式运行结果:
八、矩阵空间之间的夹角
矩阵空间之间的夹角代表两个矩阵线性相关的程度。如果夹角很小,它们之间的线性相关度就很高;反之,它们之间的线性相关度就不大。在 MATLAB 中用函数 subspace()来实现求矩阵空间之间的夹角。其调用格式如下:
- theta = subspace(A,B):返回矩阵A 和矩阵B之间的夹角。
示例9:求矩阵A和B之间的夹角
A=[1 2 3;3 4 5;7 8 9];
B=magic(3)
C=subspace(A,B) %求矩阵A和B之间的夹角运行结果: