1.离散傅里叶变换
对于离散时域信号 x[n]使用离散傅里叶变换(Discrete Fourier Transform, DFT)进行频域分析。
DFT 将离散信号 x[n] 变换为其频谱表示 X[k],定义如下:
X [ k ] = ∑ n = 0 N − 1 x [ n ] e − j 2 π k n N X[k] = \sum_{n=0}^{N-1} x[n]e^{-j\frac{2\pi kn}{N}} X[k]=∑n=0N−1x[n]e−jN2πkn
1.1 共轭对称性
对于实值信号,其离散傅里叶变换(DFT)的结果在频谱上是共轭对称性(Conjugate Symmetry)
复共轭:实数相同,虚数取反
z = a + bi, 那么 \overline{z} = a - bi
1.2 奈奎斯特频率
奈奎斯特频率(Nyquist frequency)指在采样过程中,能够精确还原原始信号的最高频率。根据奈奎斯特定理,为了正确地重建一个信号,采样频率必须至少是信号中最高频率的两倍。
因此,奈奎斯特频率就是采样频率的一半。如果信号的频谱超过了奈奎斯特频率,就会出现混叠(aliasing)现象,导致采样后的信号无法正确还原原始信号。
典型的人类语音频率范围大约在0 Hz到4 kHz之间,主要能量集中在0 Hz到2.5 kHz。
因此,为了捕捉和处理语音信号的主要频率成分,通常选择的采样频率是略大于这个最高频率(如8 kHz)。
1.3 混叠(aliasing)现象
即采样频率低于信号中最高频率的两倍,就会导致频域中的信号成分发生错位和重叠(表现为失真),从而无法正确地重建原始信号
如果采样频率低于最高频率的两倍,那么高于奈奎斯特频率的信号成分会“折叠”到采样频率范围内的其他频率位置上。
当信号频率超过了奈奎斯特频率时,它在采样后的频域中将被错误地解释为低于奈奎斯特频率的频率,这会导致信号在频域中产生额外的频率能量,这些能量是原始信号频率的镜像(或折叠)。
2.快速傅里叶变换(FFT)
FFT利用分治策略将离散傅里叶变换(DFT)分解为更小规模的DFT计算。将长度为 N 的序列分成长度为
N/2 的两个子序列,然后递归地应用FFT算法计算这两个子序列的DFT,最后将结果合并为原始序列的DFT。
- Scipy的FFT用于可视化频域图
# 使用 scipy.fftpack.fft 计算 FFT
fft_result = fft(signal)
# 计算频率轴
freqs = np.fft.fftfreq(len(signal), d=t[1] - t[0])
3.短时傅里叶变换(STFT)
短时傅里叶变换(Short-Time Fourier Transform, STFT)用于画时频谱,
是一种将信号分解到时间-频率域的方法,
参数如下:
input (Tensor):
* 输入信号,可以是 1D 或 2D 张量。
* 如果是 1D 张量,则表示单个信号序列。
* 如果是 2D 张量,第一维表示信号的批次(batch),第二维表示每个信号的时间步。
n_fft (int):
* 每个窗口的 FFT 点数。
* 通常是一个大于等于 win_length 的值。这个参数决定了频域分辨率。
hop_length (int, optional):
* 窗口之间的跳跃长度(即窗口之间的距离)。
* 默认值为 win_length // 2,即窗口重叠一半。
win_length (int, optional):
* 每个窗口的长度。
* 默认值为 n_fft, 大于n_fft, 则需要填充窗口剩余样本点。
window (Tensor, optional):
* 窗函数,用于加窗处理,以提升频谱的平滑度。
* 通常使用汉宁窗(Hann window)或汉明窗(Hamming window)。
* 默认值为一个全 1 的窗函数。
center (bool, optional):
* 如果为 True(默认值),则在信号的两端各加上 n_fft // 2 个零,以确保每个时间点都有一个完整的窗口。
pad_mode (str, optional):
* 填充模式,当 center 为 True 时使用。
* 可以是 'constant', 'reflect' 等。默认值为 'reflect'。
normalized (bool, optional):
* 如果为 True,则返回的 STFT 会进行归一化处理。
onesided (bool, optional):
* 如果为 True(默认值),则返回的 STFT 只包含非负频率部分,这在处理实数信号时是有用的。
return_complex (bool, optional):
* 如果为 True,则返回复数类型的结果。否则,返回一个两通道的实数张量,其中一个通道是实部,另一个通道是虚部。
4.代码样例
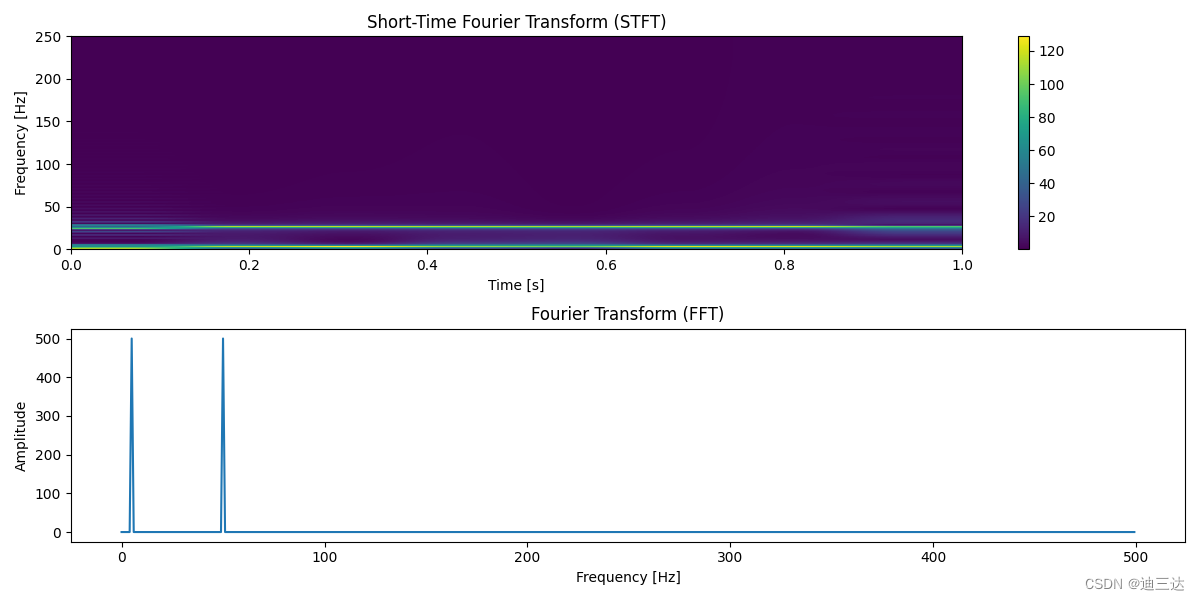
一个信号由两个信号叠加:
signal = np.sin(2 * np.pi * 5 * t) + np.sin(2 * np.pi * 50 * t)
上图为stft, 下图为fft
代码在Github_Link





![【2024最新华为OD-C/D卷试题汇总】[支持在线评测] 特殊加密算法(200分) - 三语言AC题解(Python/Java/Cpp)](https://i-blog.csdnimg.cn/direct/5d5cebb22cc749dcadd07fffea163cf4.png)